0. はじめに
苦労して制御対象のモデリングをし,制御系を設計を行ったとしても,実機を動かしてみると,様々な要因で思ったとおりに動かないということは珍しくありません.その要因のひとつは外乱です.この外乱を補償するために,外乱オブザーバを利用することが考えられます.また,最近,外乱オブザーバと同様の機構として MEC (Model Error Compensator,モデル誤差補償器) が岡島らにより提案されています.
本記事では,筆者が理解した範囲で,なるべく平易に MEC と外乱オブザーバの基本原理をさらっと説明することを試みます.そして,Simulink を利用した非線形シミュレーションによりその有効性を検証します.配布する MATLAB/Simulink ファイルは
からダウンロードしてください.R2023b, R2023a, R2022b, R2022a, R2021b, R2018a 用を用意しています.
なお,本記事の内容は
川田 昌克:零点と不安定極をもたない 2 次系に対する外乱オブザーバとモデル誤差抑制補償器の関係について,計測自動制御学会論文集,Vol.60,No.2,pp.101-103 (2024)
で議論されています.
1. ざっくりとした内容
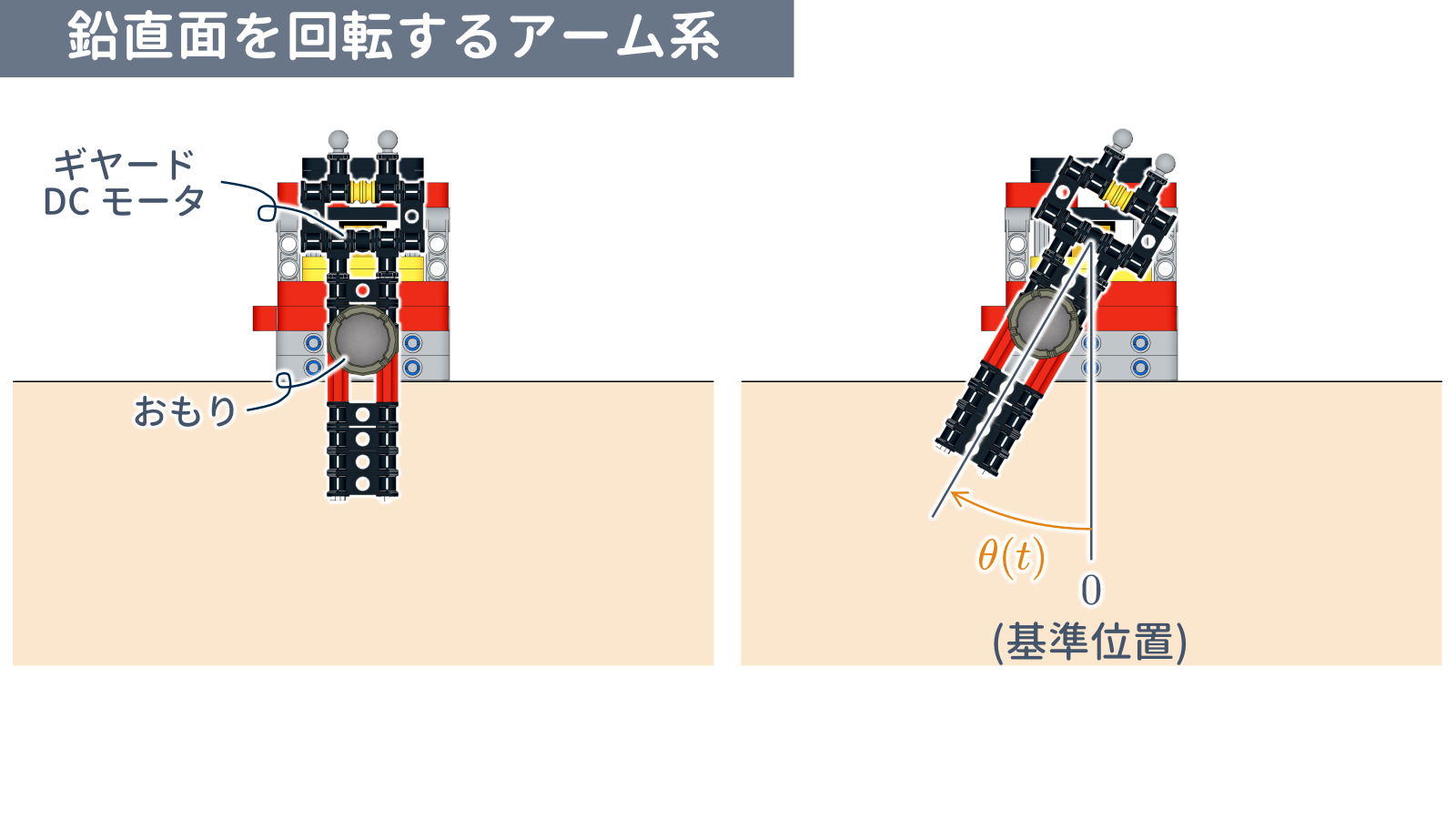
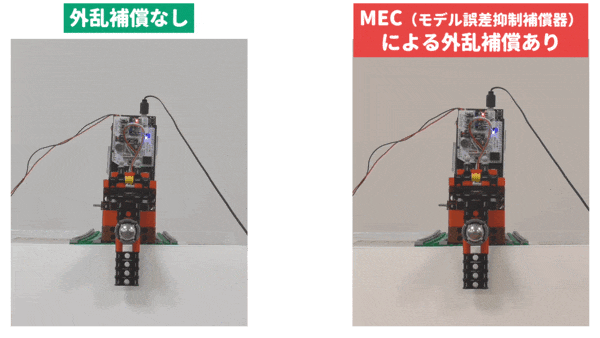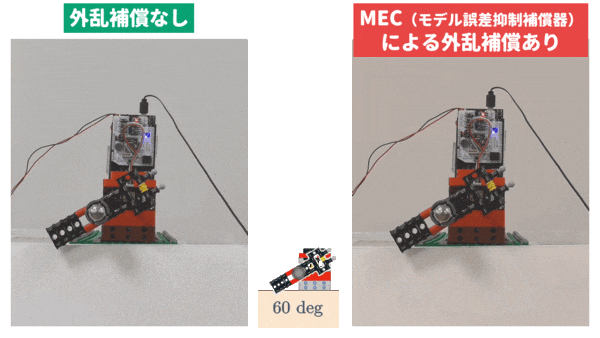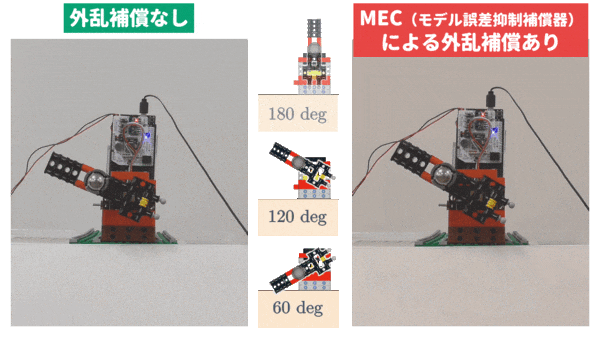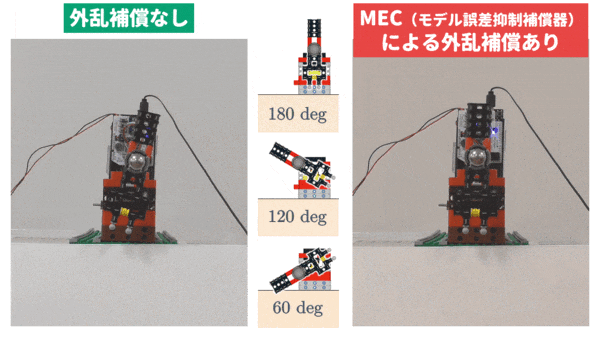
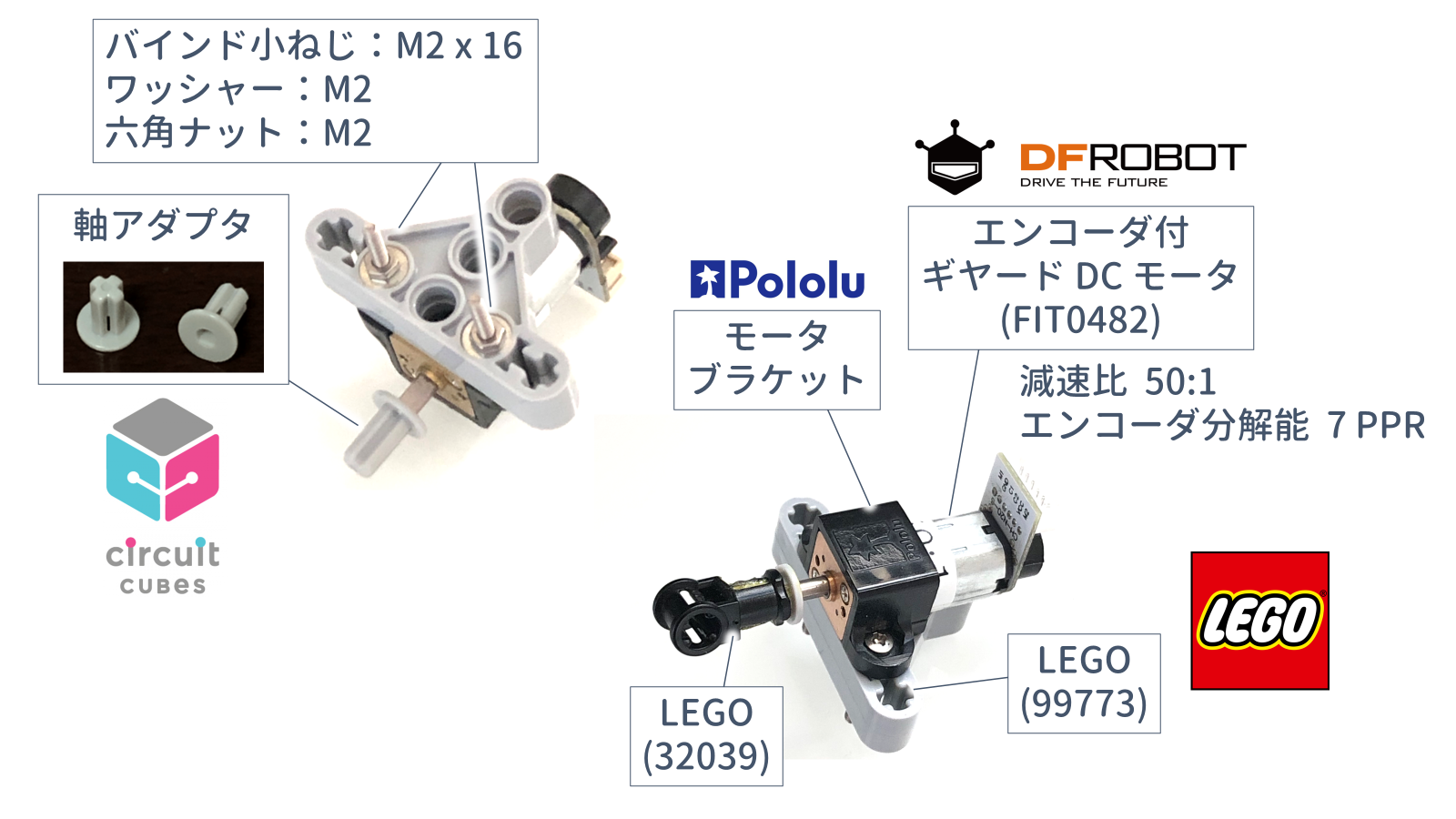
LEGO 部品で製作された「鉛直面を回転するアーム系」を制御対象とします.制御目的は,PID 制御によりアーム角 $\theta$ をステップ状に変化する目標値 $r$ に追従させることです.
アームの重力トルクはアーム角 $\theta$ に応じて非線形的に変化します.アームが真下にあるときは重力トルクが小さいのですが,アームを時計回りに水平位置まで回転させていくと,徐々に重力トルクが大きくなっていき,水平位置のときに最大となります.さらに時計回りに真上まで回転させると,徐々に重力トルクが小さくなっていき,真上位置では真下位置と同様,重力トルクは 0 となります.
このように,複雑に重力トルクが変化するので,下動画の左側の実験結果のように,単純な微分先行型 PID 制御(この例では,アームが真下近傍で動作するとして導出されるノミナルモデル(公称モデル)に対して,PID パラメータを決定しています)では,良好な制御結果を得ることができません.
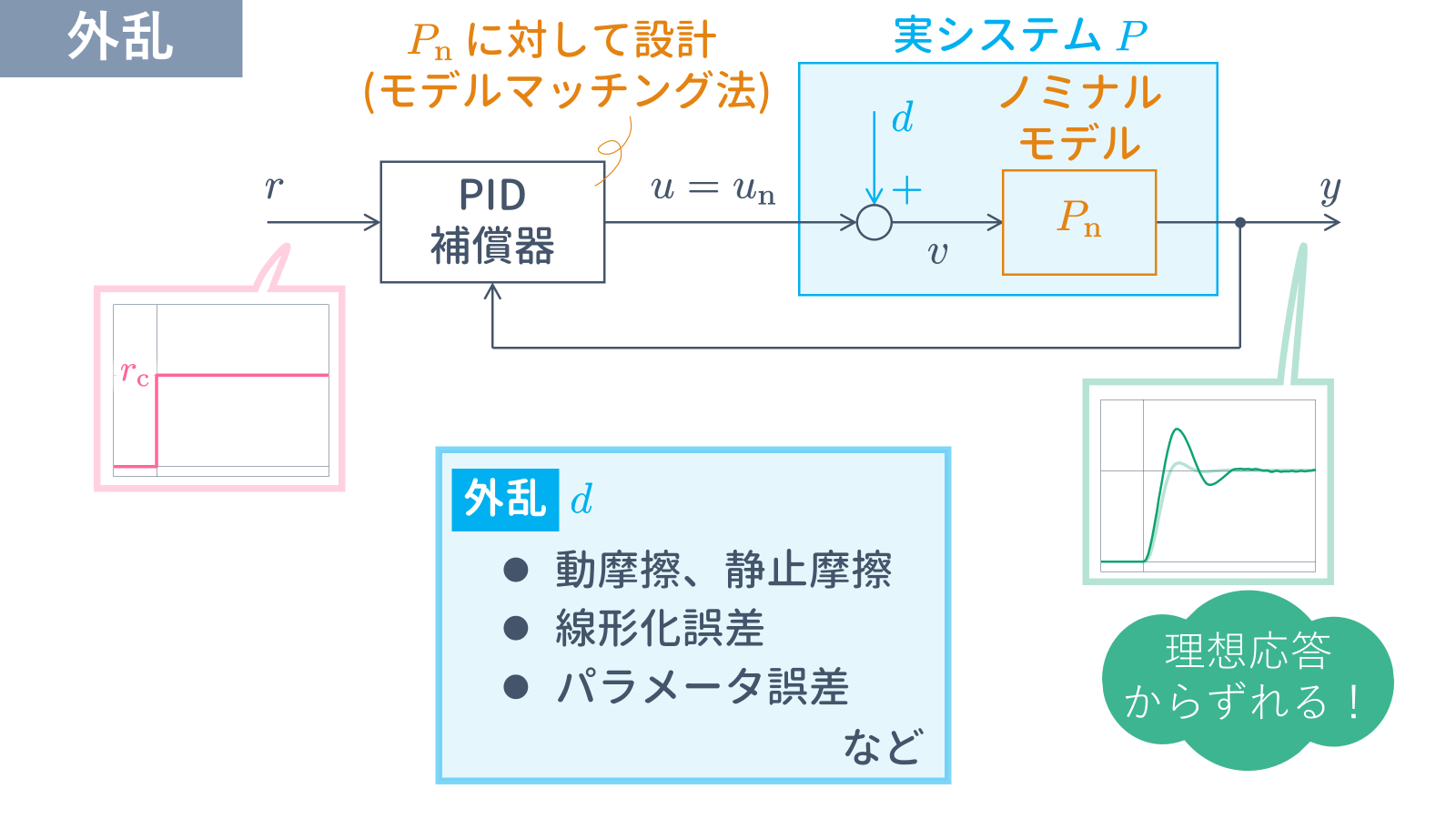
そこで,本記事では,実システム $P$ がノミナルモデル $P_{\rm n}$ に外乱 $d$ が加わったものであると考えます.そして,PID 制御系に付加された
- MEC(モデル誤差抑制補償器)
あるいは
- 外乱オブザーバ
によって外乱の推定値 $\widehat{d}$ をリアルタイムで計算します.このとき,外乱 $d$ を打ち消すように制御入力 $u$ を操作することで(このことを外乱補償といいます),制御性能を向上させます.実際に,MEC を利用して外乱補償を行った実験結果が上動画の右側です.
本記事では,
ポイント
- 外乱オブザーバの概略を説明
- MEC の概略を説明
- 外乱オブザーバと MEC の関係についての説明
- Simulink を利用した非線形シミュレーションを行い,アニメーション表示された実験結果により有効性を確認
をすることにします.
2. 「鉛直面を回転するアーム系」のモデル
「鉛直面を回転するアーム系」の数理モデルは
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
\alpha\hskip1pt\ddot{y} + \beta\hskip1pt\dot{y} + \gamma \sin{y} = u
\tag{1}
\end{align}
となります.ただし,制御出力は $y = \theta$(真下を基準としたアーム角),制御入力は $u = v$(モータドライバに加える指令電圧)です.
$(1)$ 式は非線形であるので,$y = 0$ 近傍で動作するものとして,$\sin{y} \simeq y$ のように線形近似します.その結果,ノミナルモデル(公称モデル)
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
y = {P}_{\rm n}\hskip1pt u,\
{P}_{\rm n} = \dfrac{b}{s^2 + {a}_{1}s + {a}_{0}}
\tag{2}
\end{align}
が得られます.ただし,
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
{a}_{0} = \dfrac{\gamma}{\alpha},\
{a}_{1} = \dfrac{\beta}{\alpha},\
b = \dfrac{1}{\alpha}
\end{align}
です.
3. 外乱オブザーバ
3.1 参考資料
外乱オブザーバについては文献
に様々な結果が詳しくまとめられています.
また,Qiita でもたとえば,
で紹介されています.
3.2 外乱補償
制御対象のノミナルモデル $P_{\rm n}$ と実システム $P$ のギャップが外乱 $d$ により表されているとします.
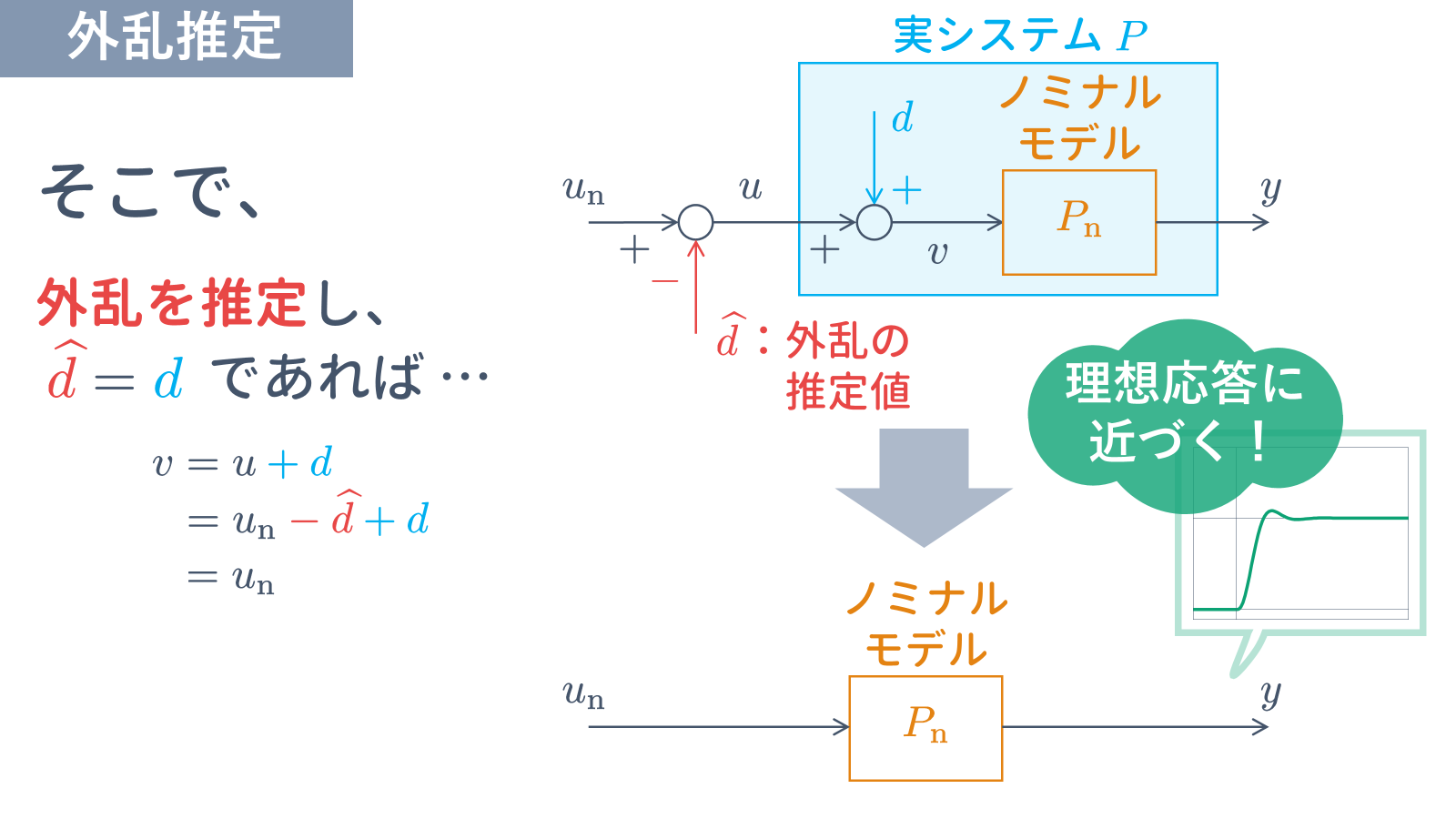
このとき,何らかの機構により外乱 $d$ を推定できれば,推定値 $\widehat{d}$ を用いて外乱補償
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
u = {u}_{\rm n} - \widehat{d}
\tag{3}
\end{align}
を行うことで,制御対象がノミナルモデルと同じ形式
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
y = P_{\rm n}\hskip1pt {u}_{\rm n}
\tag{4}
\end{align}
となります.したがって,たとえば,ノミナルモデル $P_{\rm n}$ に対してモデルマッチング法などにより設計された「微分先行型 PID コントローラ(PI-D コントローラ)」
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
% u_{\rm n} = {k}_{\rm P}\hskip1pt e
% + {k}_{\rm I}\int_{0}^{t}e\hskip1pt{\rm d}\tau
% - {k}_{\rm D}\hskip1pt\dot{y},\
u_{\rm n} = \biggl({k}_{\rm P} + \dfrac{{k}_{\rm I}}{s}\biggr)e
- {k}_{\rm D}s\hskip1pt y,\
e = r - y
\tag{5}
\end{align}
により所望の制御性能が得られることが期待できます.
なお,
PID パラメータ
\begin{align}
&
\left\{\begin{array}{l}
{k}_{\rm I}
= \dfrac{{a}_{0}}{b{\gamma}_{1}} \\
{k}_{\rm P}
= \dfrac{1}{{\gamma}_{2}}
\biggl(
\dfrac{1}{b}
- {\gamma}_{3}{k}_{\rm I}
\biggr) \\
{k}_{\rm D}
= {\gamma}_{2}{k}_{\rm I}
+ \dfrac{1}{b}\biggl(
\dfrac{{a}_{0}{k}_{\rm P}}{{k}_{\rm I}}
- {a}_{1}
\biggr)
\end{array}\right.
\tag{6} \\
&
\gamma_1 = \dfrac{{a}_{\rm m1}}{{\omega}_{\rm m}},\
\gamma_2 = \dfrac{{a}_{\rm m2}}{{\omega}_{\rm m}^{2}},\
\gamma_3 = \dfrac{1}{{\omega}_{\rm m}^{3}}
\end{align}
と選ぶと,PI-D 制御系の目標値伝達関数
\begin{align}
{G}_{yr} &= \dfrac{{P}_{\rm n}\biggl({k}_{\rm P}
+ \dfrac{{k}_{\rm I}}{s}\biggr)}
{1 + {P}_{\rm n}\biggl({k}_{\rm P}
+ \dfrac{{k}_{\rm I}}{s}
+ {k}_{\rm D}s\biggr)}
\\
&= \dfrac{b{k}_{\rm P}s + b{k}_{\rm I}}
{s^3 + ({a}_{1} + b{k}_{\rm D})s^2
+ ({a}_{0} + b{k}_{\rm P})s
+ b{k}_{\rm I}}
\tag{7}
\end{align}
の逆数は近似的に 3 次の規範モデル
\begin{align}
{M}_{3} = \dfrac{{\omega}_{\rm m}^{3}}
{s^3 + {a}_{\rm m2}{\omega}_{\rm m}s^2
+ {a}_{\rm m1}{\omega}_{\rm m}^{2}s
+ {\omega}_{\rm m}^{3}}
\tag{8}
\end{align}
の逆数と一致します ($1/G_{yr} \simeq 1/M_3$).
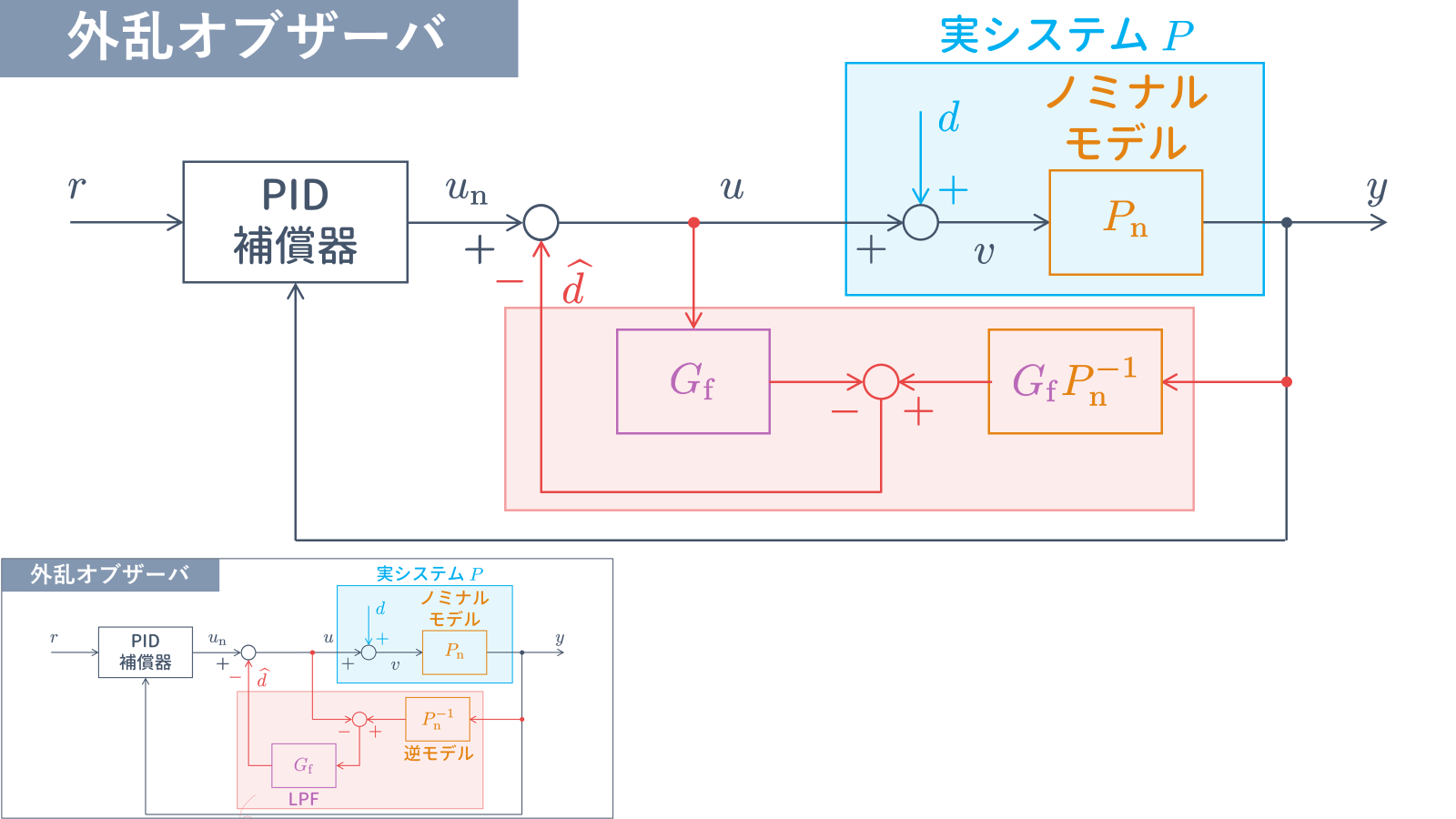
3.3 外乱オブザーバの構成
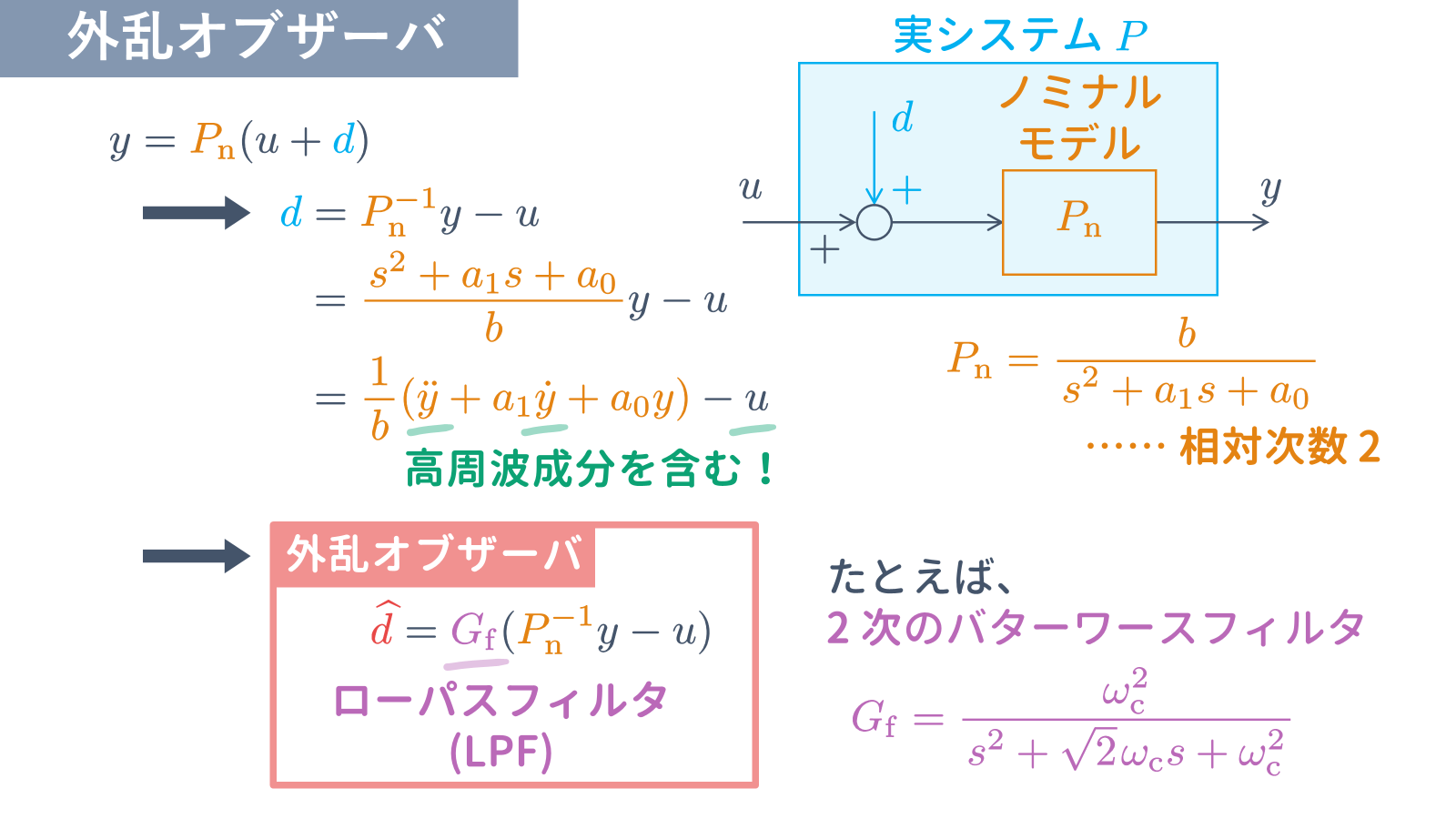
外乱推定を行う機構として外乱オブザーバが知られています.外乱オブザーバは制御対象の入出力信号 $u$, $y$ から外乱の推定値 $\widehat{d}$ を計算します.
制御対象の入出力関係が
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
y = P_{\rm n}(u + d)
\tag{9}
\end{align}
であるとします.そして,$(9)$ 式を外乱 $d$ について解くと,
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
d = {P}_{\rm n}^{-1}y - u
\tag{10}
\end{align}
が得られます.したがって,$(10)$ 式により外乱 $d$ が計算できると考えられるのですが,
- $P_{\rm n}^{-1}y$ には微分項が含まれるので,高周波成分が問題となります(下図における $s$ は微分演算子 $s = {\rm d}/{\rm d}t$ とします)
- PID 補償器を利用する場合,微分動作により制御入力 $u$ に高周波成分が含まれます
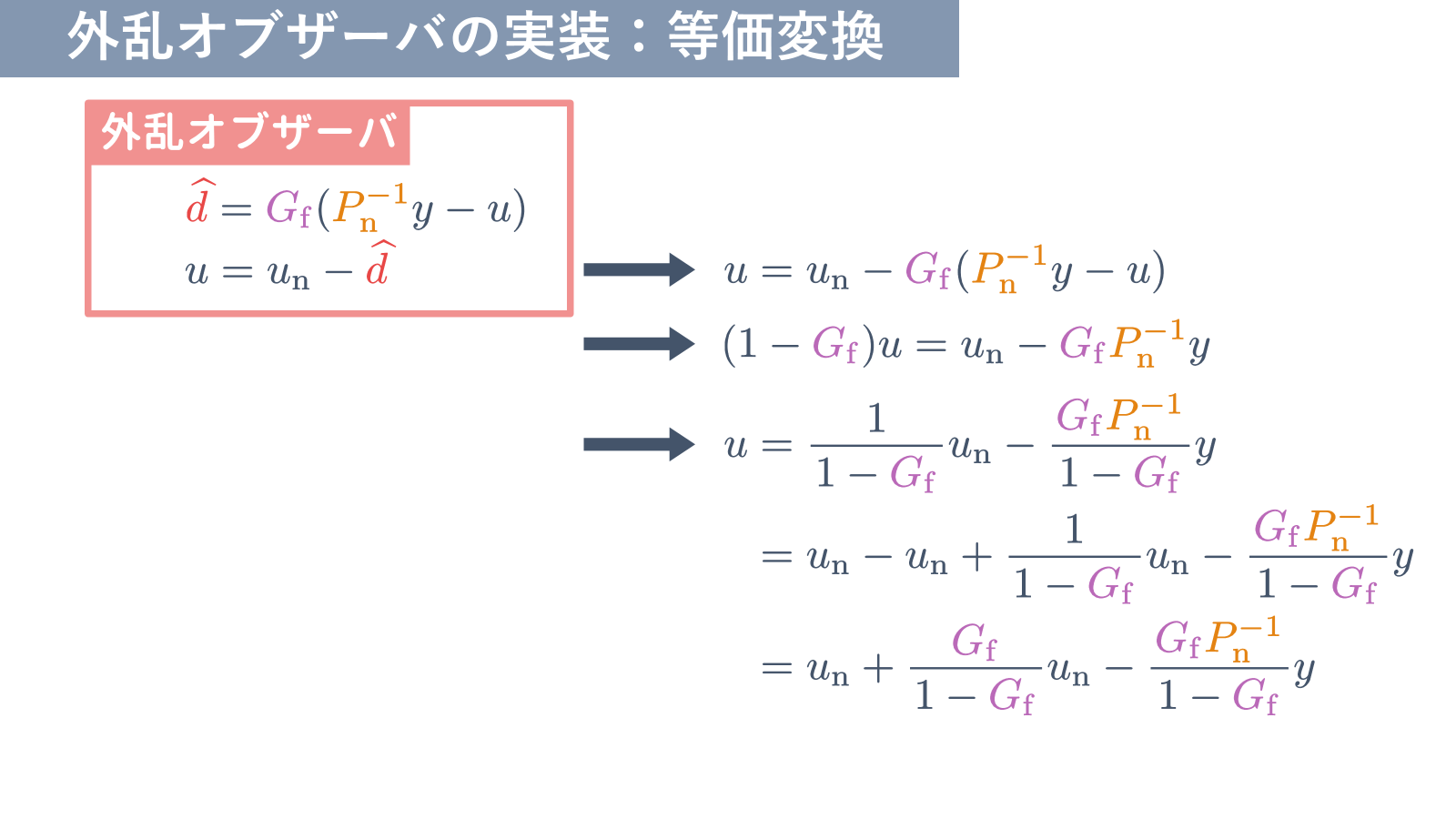
ので,このまま実装すると(微分項を数値微分で実装すると),激しいチャタリングが生じてしまい,使い物になりません.そこで,ローパスフィルタ $G_{\rm f}$ を利用して $G_{\rm f}P_{\rm n}^{-1}$ がプロパー(分子の次数が分母の次数を超えない)となるようにします.
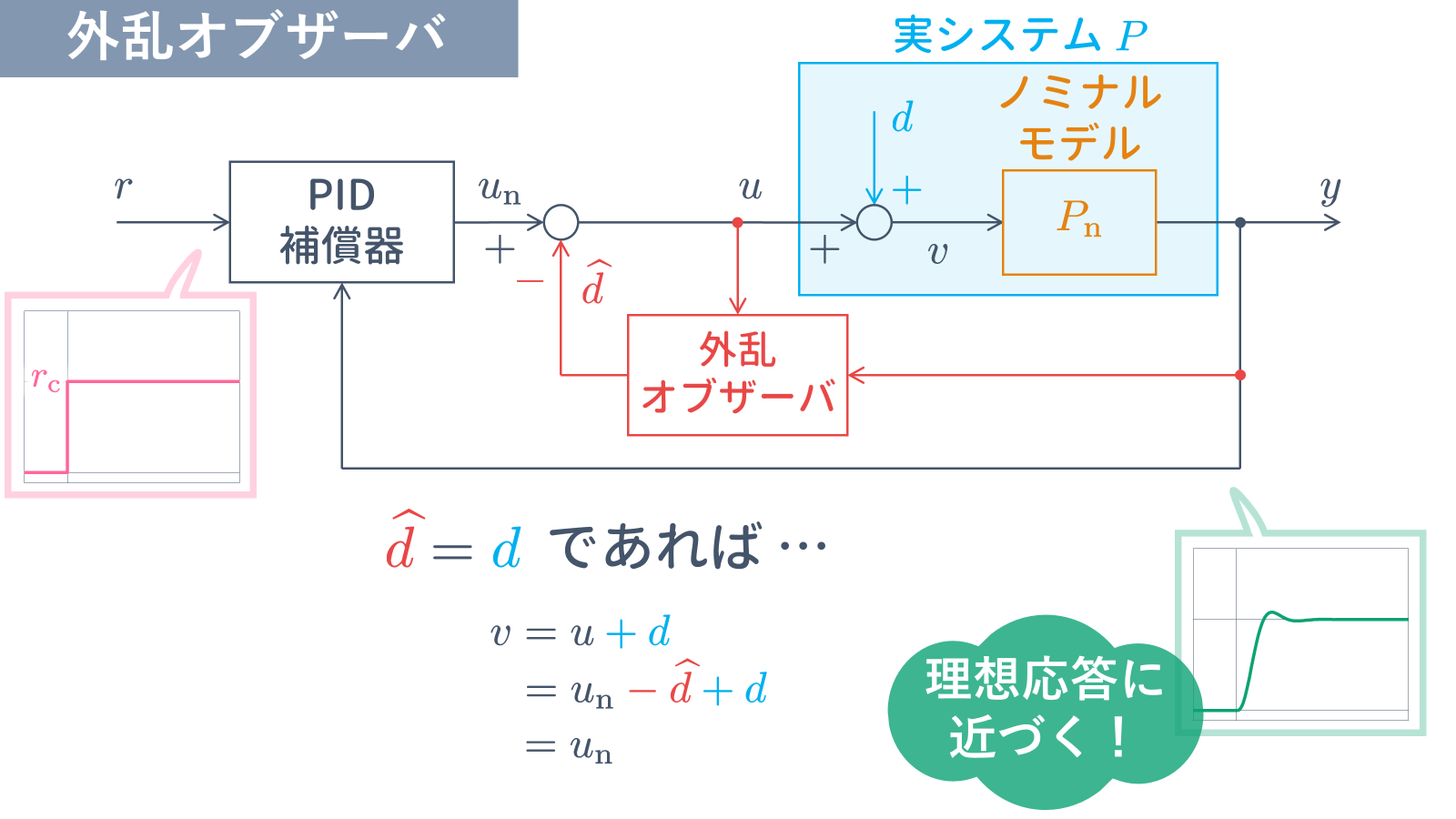
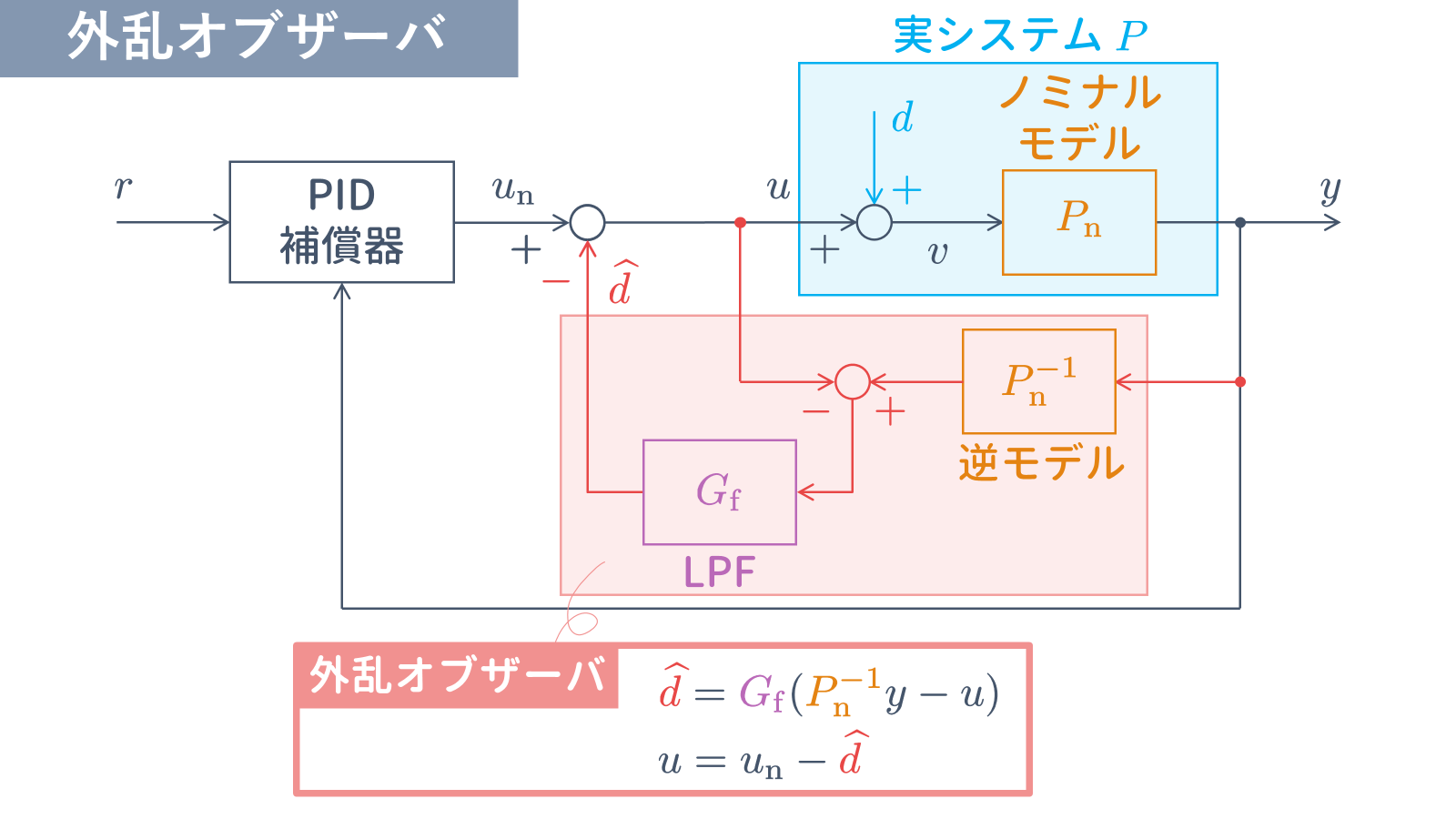
このようにして構成された外乱推定機構を外乱オブザーバといい,
外乱オブザーバ
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
u = {u}_{\rm n} - \widehat{d},\
\widehat{d} = {G}_{\rm f}\hskip1pt({P}_{\rm n}^{-1}y - u)
\tag{11}
\end{align}
となります.
また,「鉛直面を回転するアーム系」のノミナルモデルは 2 次遅れ要素
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
{P}_{\rm n} = \dfrac{b}{s^2 + {a}_{1}s + {a}_{0}}
\end{align}
であり,その相対次数(分母と分子の次数差)は $2$ です.したがって,以下では,$G_{\rm f}P_{\rm n}^{-1}$ がプロパーとなるようなローパスフィルタとして,2 次のバターワースフィルタ
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
{G}_{\rm f} = \dfrac{{\omega}_{\rm c}^{2}}
{s^2 + \sqrt{2}\hskip1pt{\omega}_{\rm c}\hskip1pts + {\omega}_{\rm c}^{2}}
\tag{12}
\end{align}
を用いることにします.$(12)$ 式を用いて外乱オブザーバ $(11)$ 式を実装すると,カットオフ角周波数 $\omega_{\rm c}$ が設計パラメータとなります.
4. MEC(モデル誤差補償器)
MEC (Model Error Compensator,モデル誤差補償器) は岡島先生らのグループにより提案された機構であり,外乱オブザーバと同様,たとえば,PID 制御系に MEC を付加することで,モデル化誤差や外乱に対してロバスト性を向上させることができます.
4.1 参考資料
MEC については文献
- 岡島 寛:モデル誤差抑制補償器を用いた既存制御系のロバスト化,計測と制御,Vol.62,No.3,pp.168-175 (2023)
や岡島先生のサイト
に様々な結果が詳しくまとめられています.
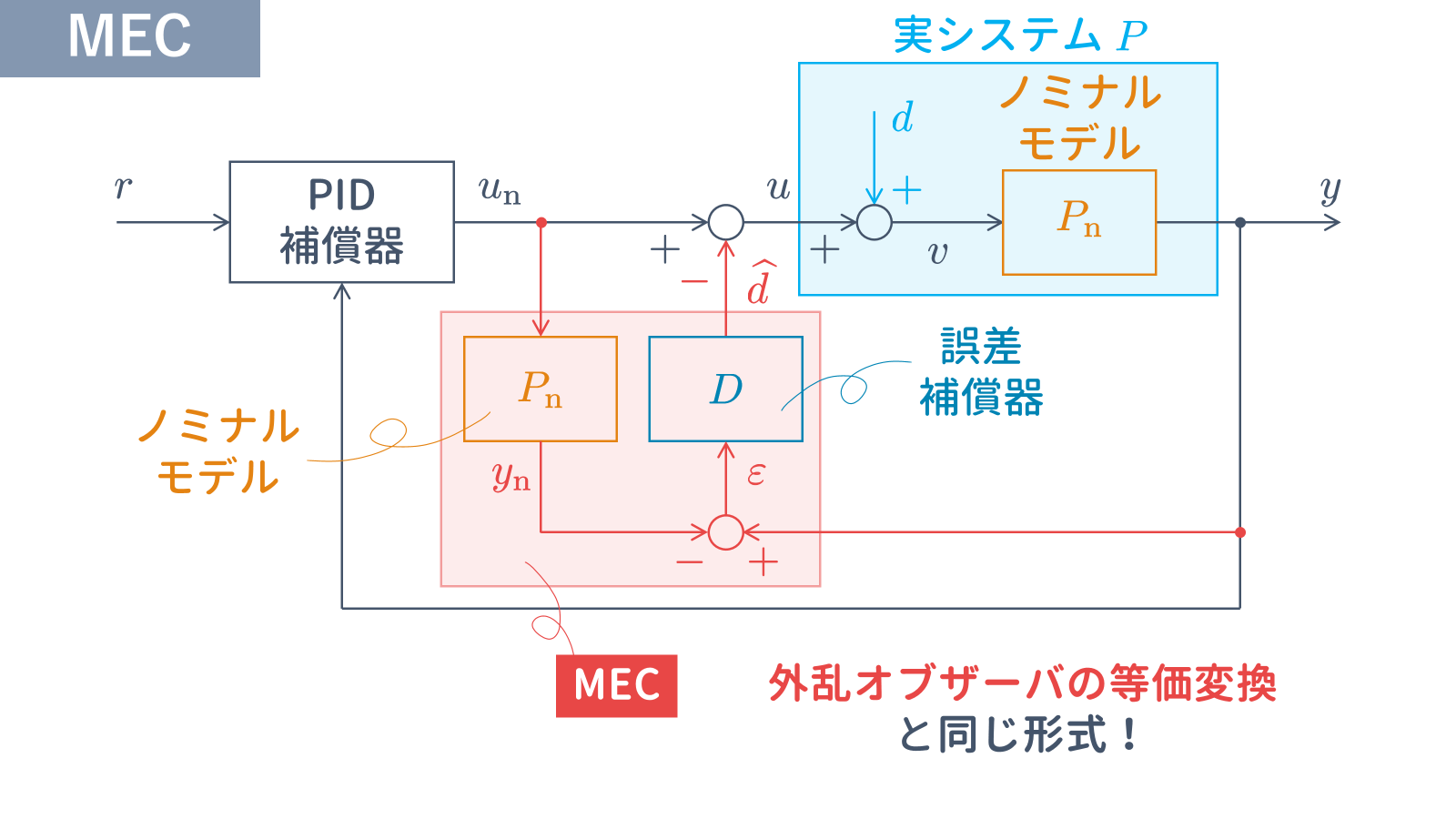
4.2 MEC
外乱オブザーバと同様の外乱推定機構として
MEC(モデル誤差抑制補償器)
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
u = {u}_{\rm n} - \widehat{d},\
\widehat{d} = D\hskip1pt\varepsilon,\
\left\{\begin{array}{l}
\varepsilon = y - {y}_{\rm n} \\
{y}_{\rm n} = {P}_{\rm n}{u}_{\rm n}
\end{array}\right.
\tag{13}
\end{align}
が岡島らにより提案されています.ここで,$D$ は誤差補償器と呼ばれます.
原著では,
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
P = {P}_{\rm n} + \varDelta{P}
\tag{14}
\end{align}
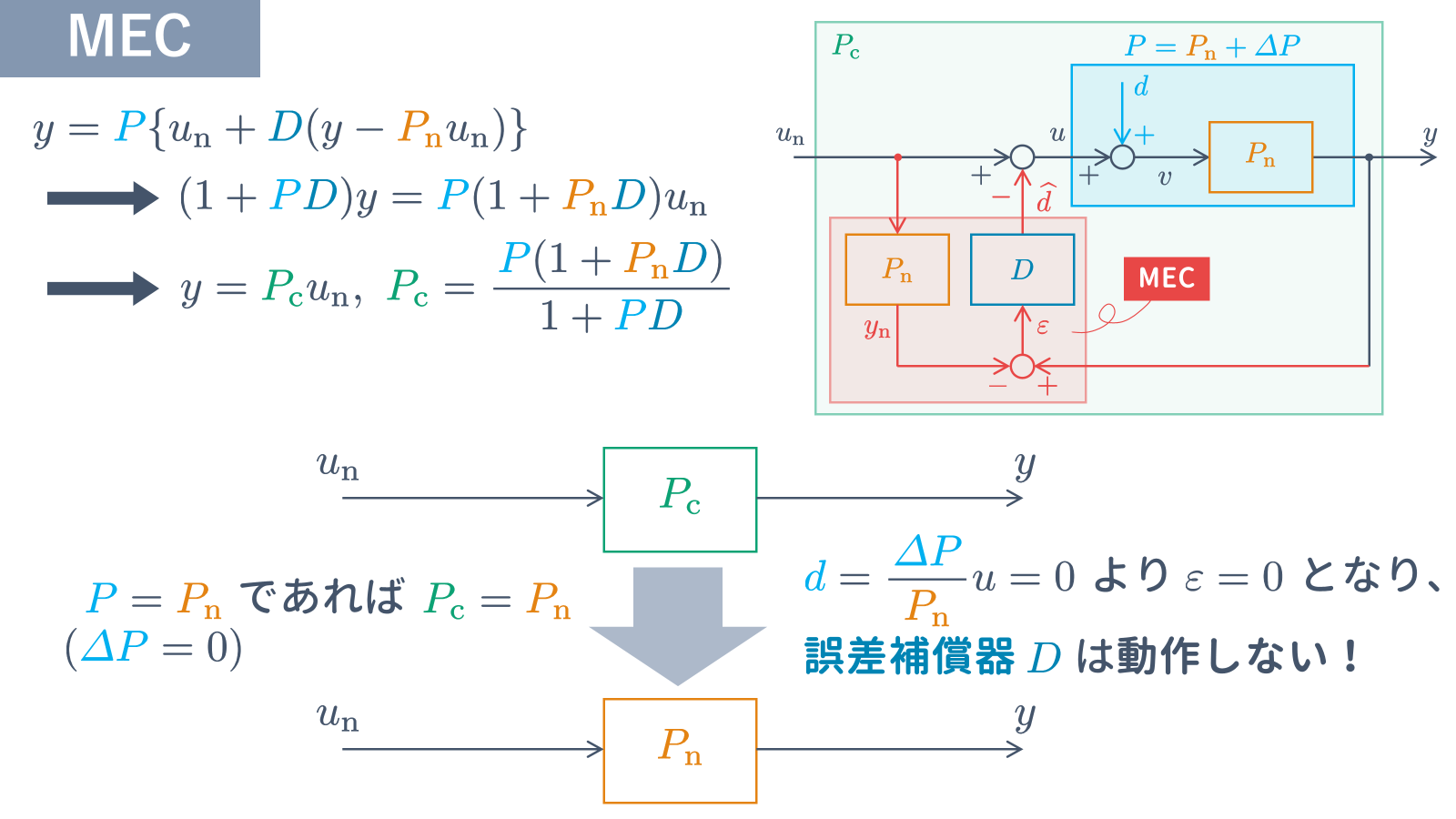
という場合を考えています.本記事の記述にあわせると,
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
y &= Pu = ({P}_{\rm n} + \varDelta{P})u
\\
&= {P}_{\rm n}(u + d),\
d = \dfrac{\varDelta{P}}{{P}_{\rm n}}u
\tag{15}
\end{align}
のようにモデル化誤差 $\varDelta{P}$ により生成される外乱 $d$ を考慮していることになります.
MEC $(13)$ 式を用いると,以下のように,誤差補償器 $D$ をハイゲインとすることで,モデル化誤差 $\varDelta{P}$ の影響を抑制できることがわかります.
誤差補償器 $D$ としては,たとえば,次式のような形式が用いられます.
誤差補償器 $D$ の形式の一例
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
\mbox{P 型:}&\ D = {k}_{\rm P2}
\tag{16}\\
\mbox{PI 型:}&\ D = {k}_{\rm P2}
+ \dfrac{{k}_{\rm I2}}{s}
\tag{17}\\
\mbox{PD 型:}&\ D = {k}_{\rm P2}
+ {k}_{\rm D2}\dfrac{s}{1 + {T}_{\rm f2}s}
\tag{18}\\
\mbox{PID 型:}&\ D = {k}_{\rm P2}
+ \dfrac{{k}_{\rm I2}}{s}
+ {k}_{\rm D2}\dfrac{s}{1 + {T}_{\rm f2}s}
\tag{19}
\end{align}
ただし,ハイゲインである誤差補償器 $D$ において,微分動作はチャタリングを生じさせる要因となります.したがって,実用上,P 型や PI 型の誤差補償器 $D$ を使用することが望ましいでしょう.
5. MEC と外乱オブザーバの関係
本章の内容は
- 川田 昌克:零点と不安定極をもたない 2 次系に対する外乱オブザーバとモデル誤差抑制補償器の関係について,計測自動制御学会論文集,Vol.60,No.2,pp.101-103 (2024)
で議論されています.
5.1 外乱オブザーバの別表現
松井らは
- 松井 義弘,綾野 秀樹:外乱オブザーバの実装法について,電気学会研究会資料,CT18022, pp.77-80 (2018)
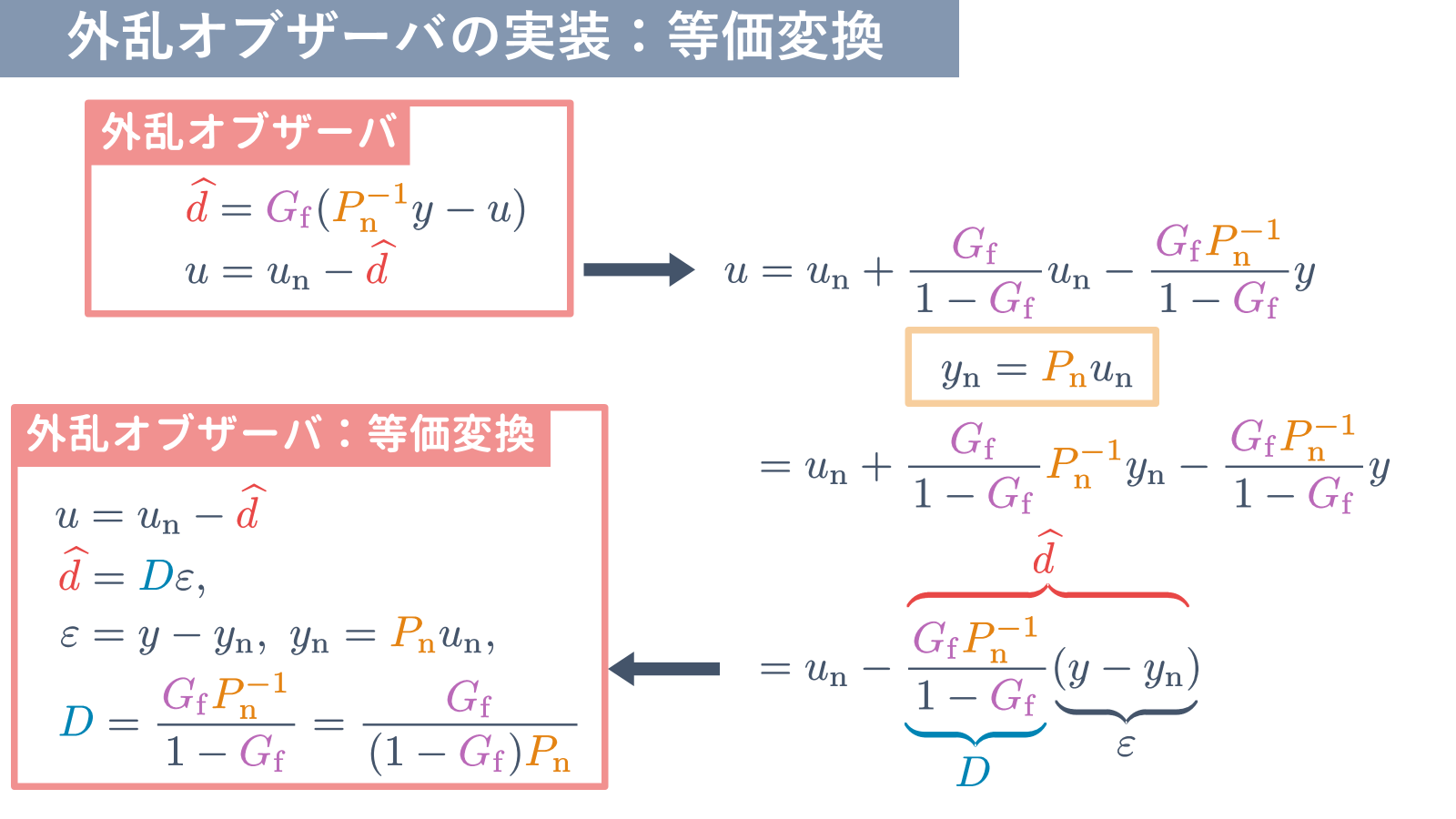
で外乱オブザーバ $(11)$ 式を書き換えると,
外乱オブザーバ $(11)$ 式の別表現
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
u &= {u}_{\rm n} - \widehat{d},\
\widehat{d} = D\hskip1pt\varepsilon,\
\left\{\begin{array}{l}
\varepsilon = y - {y}_{\rm n} \\
{y}_{\rm n} = {P}_{\rm n}{u}_{\rm n}
\end{array}\right.
\\
D &= \dfrac{{G}_{\rm f}{P}_{\rm n}^{-1}}
{1 - {G}_{\rm f}}
= \dfrac{{G}_{\rm f}}{(1 - {G}_{\rm f}){P}_{\rm n}}
\tag{20}
\end{align}
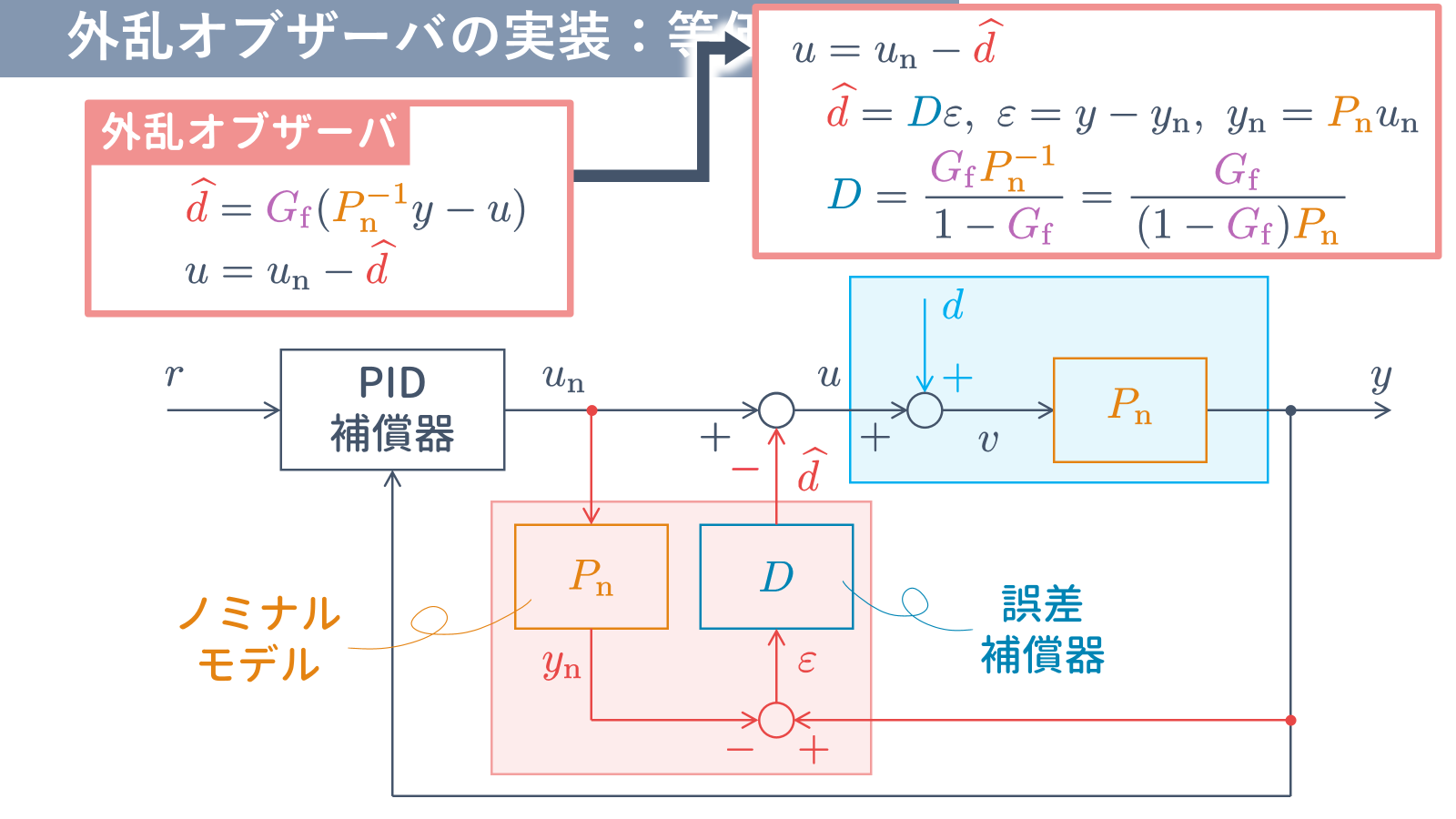
となることを示しています.外乱オブザーバの別表現 $(20)$ 式は,MEC $(13)$ 式と同じ形式であることがわかります.
5.2 外乱オブザーバを MEC で表現すると…
たとえば,外乱オブザーバにおけるローパスフィルタ $G_{\rm f}$ として,2 次のバターワースフィルタ $(12)$ 式を与えると,結果として PID 型の誤差補償器
\begin{align}
D &= \dfrac{{G}_{\rm f}}{(1 - {G}_{\rm f}){P}_{\rm n}}
= {k}_{\rm P2}
+ \dfrac{{k}_{\rm I2}}{s}
+ {k}_{\rm D2}\dfrac{s}{1 + {T}_{\rm f2}s}
\tag{21}\\
{T}_{\rm f2} &= \dfrac{1}{\sqrt{2}\hskip1pt{\omega}_{\rm c}},\
{k}_{\rm I2} = \dfrac{{\omega}_{\rm c}}
{\sqrt{2}{\hskip1pt}b}
{a}_{0},\
{k}_{\rm P2} =
\dfrac{{\omega}_{\rm c}}
{\sqrt{2}{\hskip1pt}b}
\biggl(
{a}_{1}
- \dfrac{{a}_{0}}
{\sqrt{2}\hskip1pt{\omega}_{\rm c}}
\biggr),\
\\
{k}_{\rm D2} &=
\dfrac{{\omega}_{\rm c}}
{\sqrt{2}{\hskip1pt}b}
\biggl\{
1
- \dfrac{1}{\sqrt{2}\hskip1pt{\omega}_{\rm c}}
\biggl(
{a}_{1}
- \dfrac{{a}_{0}}
{\sqrt{2}\hskip1pt{\omega}_{\rm c}}
\biggr)
\biggr\}
\end{align}
を用いた MEC を設計していることになります.
先に述べたように,外乱オブザーバでは,2 次のバターワースフィルタ $(12)$ 式を用いると,カットオフ角周波数 $\omega_{\rm c}$ が設計パラメータとなります.外乱の推定を素早く行うためには,$\omega_{\rm c}$ をある程度大きな値に設定する必要があります.
$\omega_{\rm c}$ を大きくすると,$k_{\rm I2}$, $k_{\rm P2}$, $k_{\rm D2}$ は $\omega_{\rm c}$ にほぼ比例して大きくなります.一方,$T_{\rm f2}$ は $0$ に近づきます.したがって,$\omega_{\rm c}$ を大きくしすぎると,誤差補償器 $D$ の微分動作
\begin{align}
{k}_{\rm D2}\dfrac{s}{1 + {T}_{\rm f2}s}
\end{align}
によって生じるチャタリング(高周波振動)が大きくなってしまい,実用上,好ましくないことがわかります.
$\omega_{\rm c}$ の値をどうするのかという塩梅が制御対象によってはもどかしいのではないかと思います.
5.3 MEC を外乱オブザーバで表現すると…
$(19)$ 式より誤差補償器 $D$ が与えられると,外乱オブザーバにおけるローパスフィルタが
\begin{align}
{G}_{\rm f} = \dfrac{{P}_{\rm n}D}{1 + {P}_{\rm n}D}
\tag{22}
\end{align}
のように求まります.たとえば,PI 型の MEC $(17)$ 式が与えられると,ローパスフィルタ ${G}_{\rm f}$ は相対次数 2 の
\begin{align}
{G}_{\rm f} = \dfrac{{P}_{\rm n}D}{1 + {P}_{\rm n}D}
= \dfrac{{k}_{\rm I2} + {k}_{\rm P2}s}
{{k}_{\rm I2}
+ (\gamma + {k}_{\rm P2})s + \beta{s}^2
+ \alpha{s}^3}
\tag{23}
\end{align}
となります.P 型,PD 型,PID 型の MEC を利用した場合も,同様にローパスフィルタ ${G}_{\rm f}$ は相対次数 2 となります.詳細は文献を参照してください.
6. Simulink を利用した非線形シミュレーション
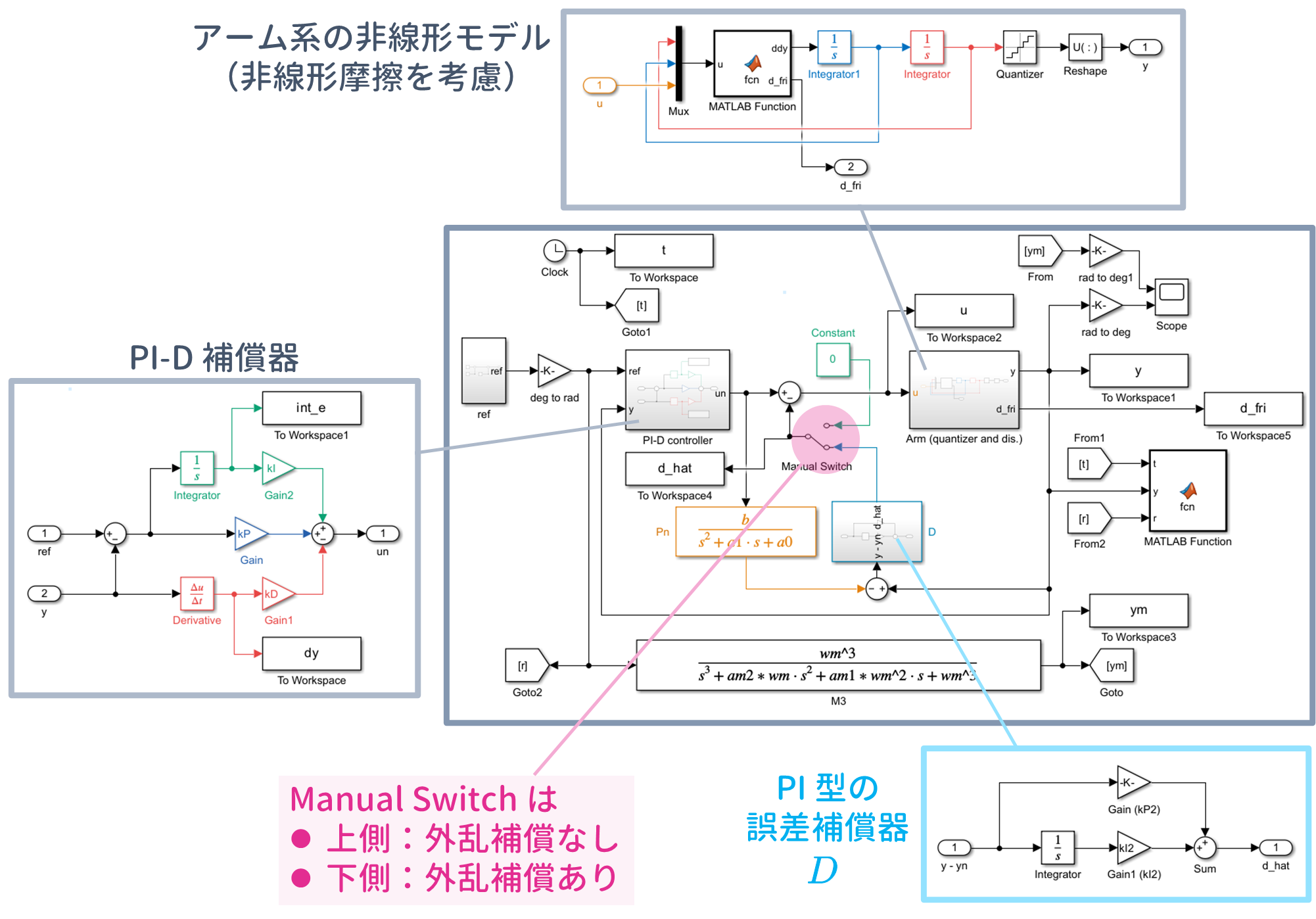
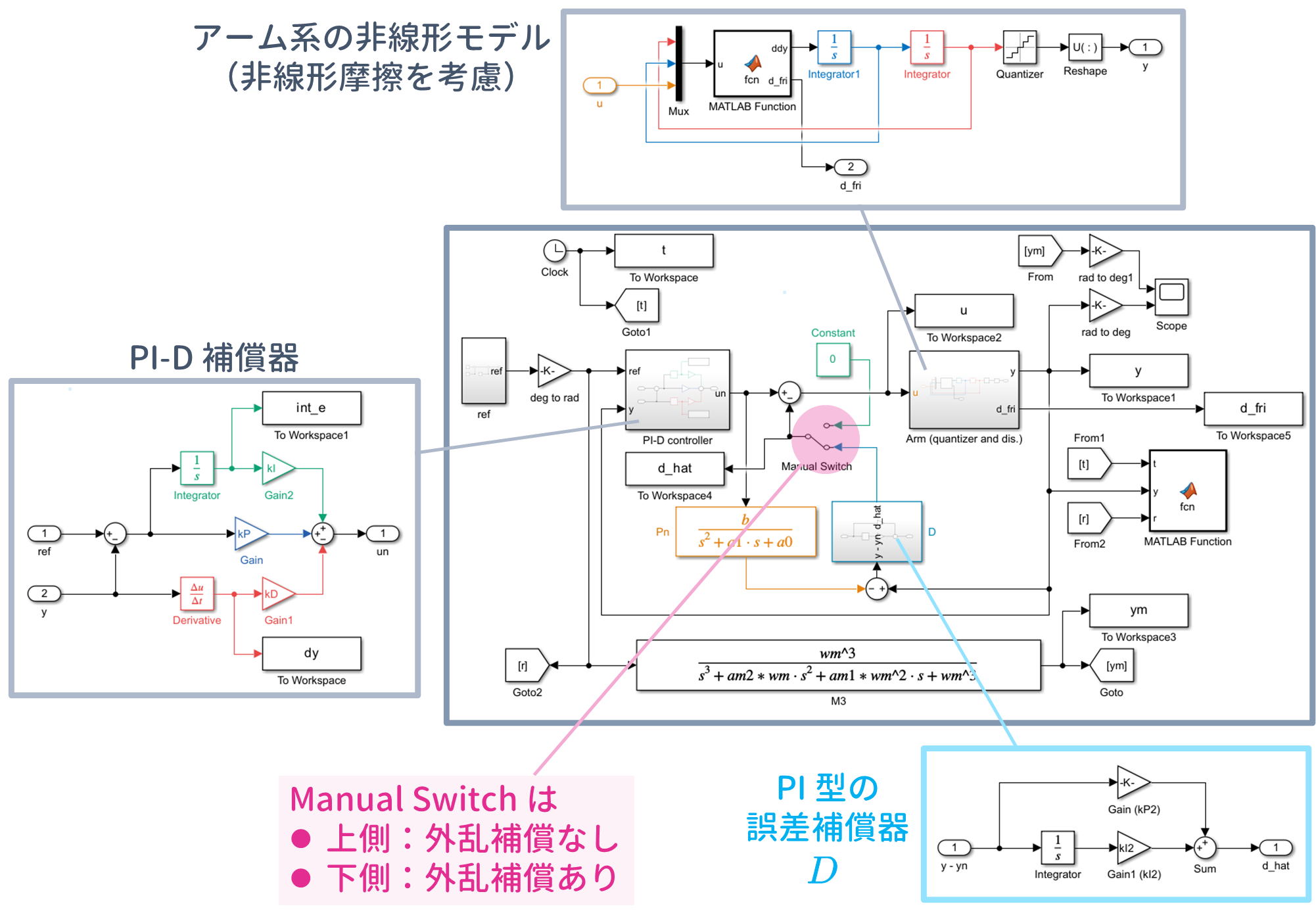
6.1 制御対象の Simulink による表現
非線形シミュレーションを行うにあたって,Simulink モデルの制御対象の部分は以下の 2 つの事項を考慮しました.
(a) 非線形摩擦
非線形摩擦としては,
で説明されている
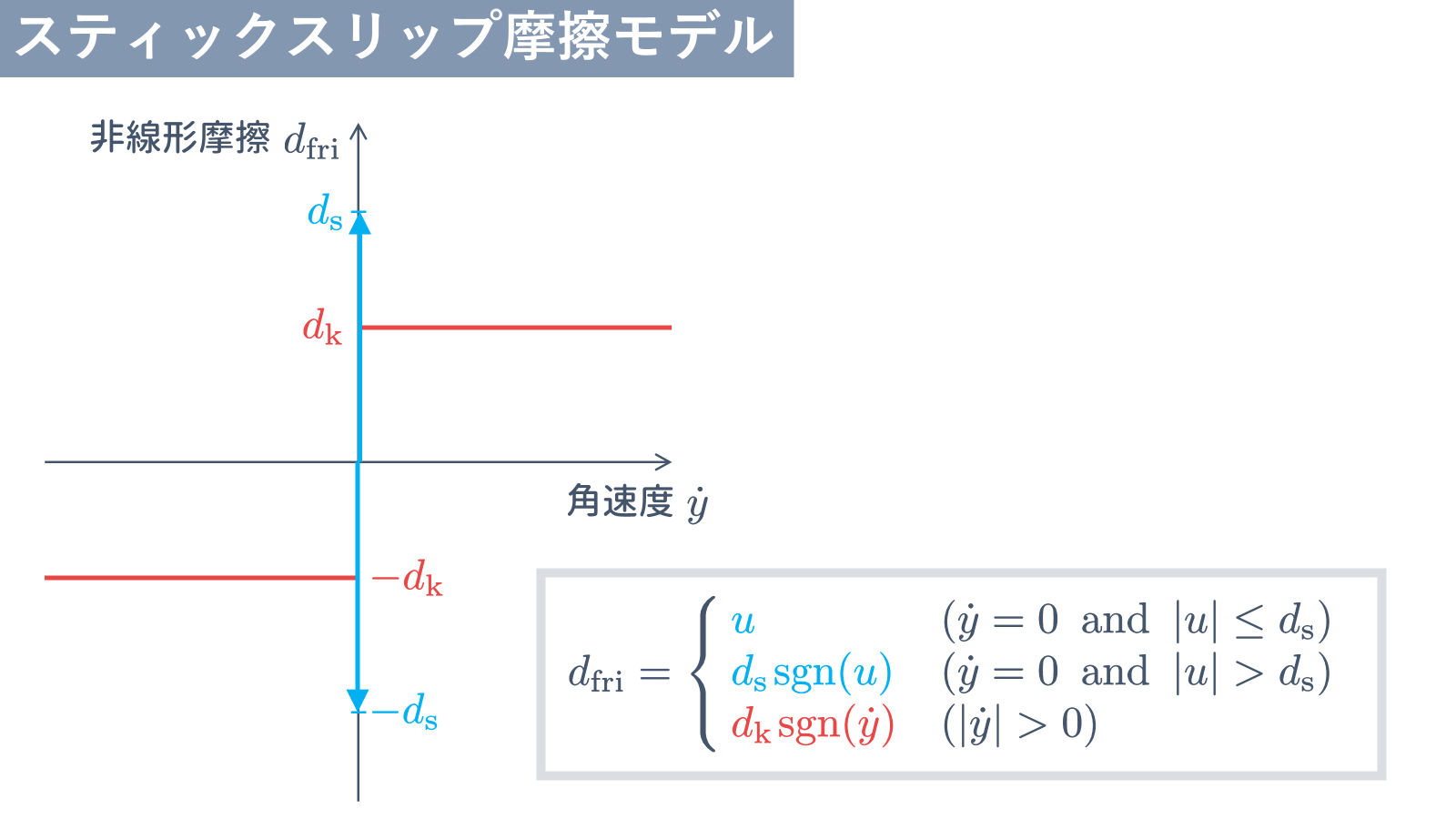
スティックスリップ摩擦モデル
\begin{align}
d_{\rm fri} = \left\{\begin{array}{ll}
u & (\dot{y} = 0 \hskip5pt\mbox{and}\hskip5pt |u| \le d_{\rm s}) \\
d_{\rm s}\hskip1pt{\rm sgn}(u) &
(\dot{y} = 0 \hskip5pt\mbox{and}\hskip5pt |u| > d_{\rm s}) \\
d_{\rm k}\hskip1pt{\rm sgn}(\dot{y}) &
(|\dot{y}| > \epsilon) \\
\end{array}\right.
\tag{24}
\end{align}
もしくは
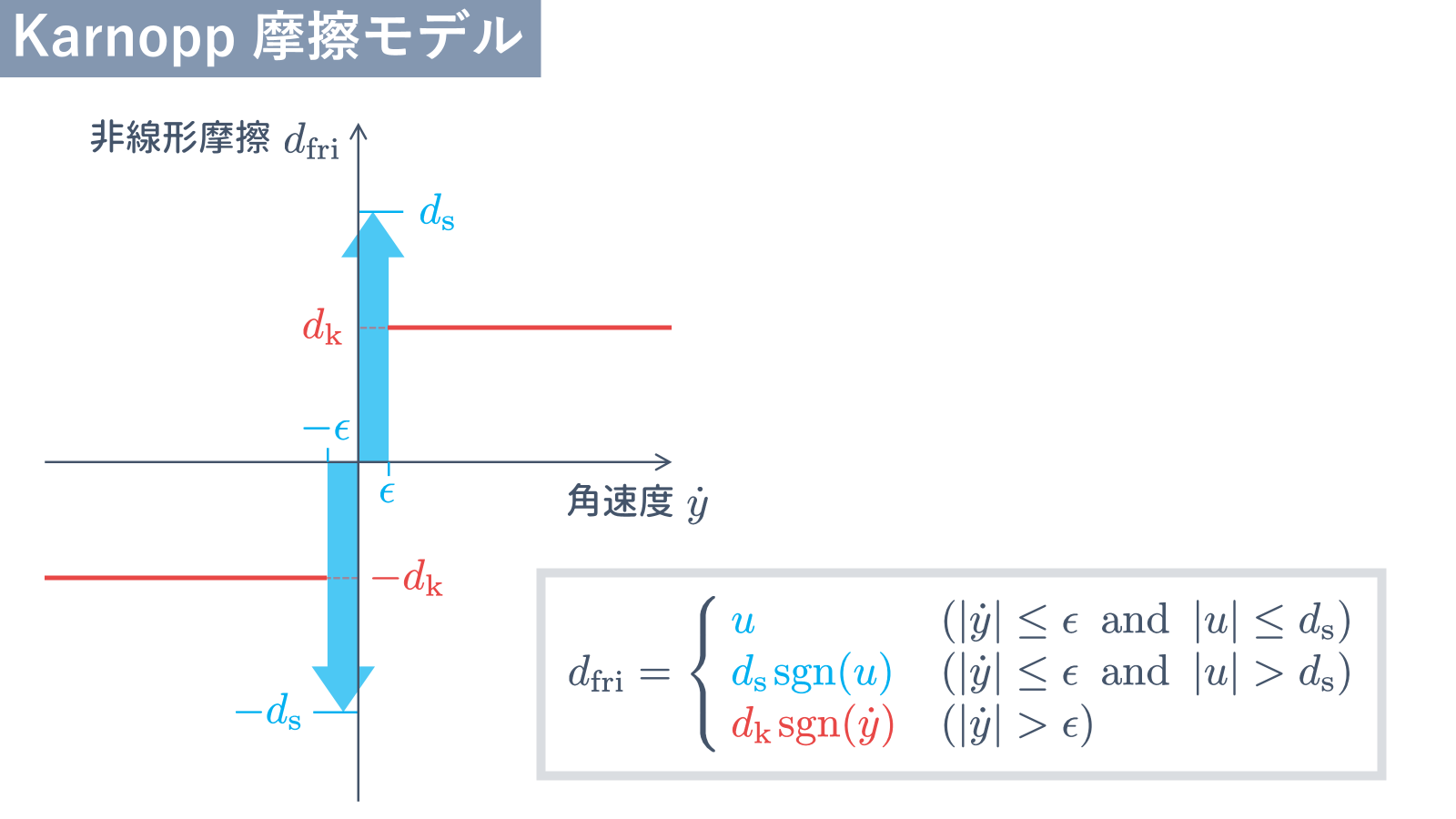
Karnopp 摩擦モデル
\begin{align}
d_{\rm fri} = \left\{\begin{array}{ll}
u & (|\dot{y}| \le \epsilon \hskip5pt\mbox{and}\hskip5pt |u| \le d_{\rm s}) \\
d_{\rm s}\hskip1pt{\rm sgn}(u) &
(|\dot{y}| \le \epsilon \hskip5pt\mbox{and}\hskip5pt |u| > d_{\rm s}) \\
d_{\rm k}\hskip1pt{\rm sgn}(\dot{y}) &
(|\dot{y}| > \epsilon) \\
\end{array}\right.
\tag{25}
\end{align}
を考慮しています.ただし,最大静止摩擦を $d_{\rm s}$,動摩擦を $d_{\rm k}$ としています.また,$\epsilon$ は微小な正数であり,${\rm sgn}(\cdot)$ は符号関数
\begin{align}
{\rm sgn}(x) = \left\{\begin{array}{rl}
1 & (x > 0) \\
0 & (x = 0) \\
-1 & (x < 0) \\
\end{array}\right.
\end{align}
です.
配布する Simulink モデル
- sim_arm_pi_d_cont_mm3rd_MEC_Quantizer.slx
- sim_arm_pi_d_cont_mm3rd_DOB_Quantizer.slx
- sim_arm_pi_d_cont_mm3rd_DOB2_Quantizer.slx
では,ブロック $\tt MATLAB\ Function$ により $(1)$ 式において非線形摩擦を加えた非線形微分方程式
\begin{align}
\require{color}
\definecolor{myred}{rgb}{0.9098,0.2784,0.2745}
\definecolor{myblue}{rgb}{0,0.4392,0.7529}
\definecolor{mygreen}{rgb}{0.0471,0.6353,0.4549}
\definecolor{mypink}{rgb}{1,0.4,0.6}
\definecolor{myskyblue}{rgb}{0,0.6902,0.9412}
\definecolor{mydarkpink}{rgb}{0.8902,0.1765,0.5686}
% =================================================
& \alpha\hskip1pt\ddot{y} + \beta\hskip1pt\dot{y} + \gamma \sin{y}
= u - {d}_{\rm fri}
\\
& \qquad
\Longrightarrow \quad
\ddot{y} + {a}_{1}\hskip1pt\dot{y} + {a}_{0} \sin{y}
= b(u - {d}_{\rm fri})
\\
& \qquad
\Longrightarrow \quad
\ddot{y} = b(u - {d}_{\rm fri})
- {a}_{0} \sin{y} - {a}_{1}\hskip1pt\dot{y}
\tag{26}
\end{align}
を実装しています.なお,外乱 $d$ は $(26)$ 式と $(1)$ 式の差分
\begin{align}
d = \gamma(y - \sin{y}) - d_{\rm fri}
\tag{27}
\end{align}
となります.すなわち,外乱 $d$ は線形化誤差と非線形摩擦です.
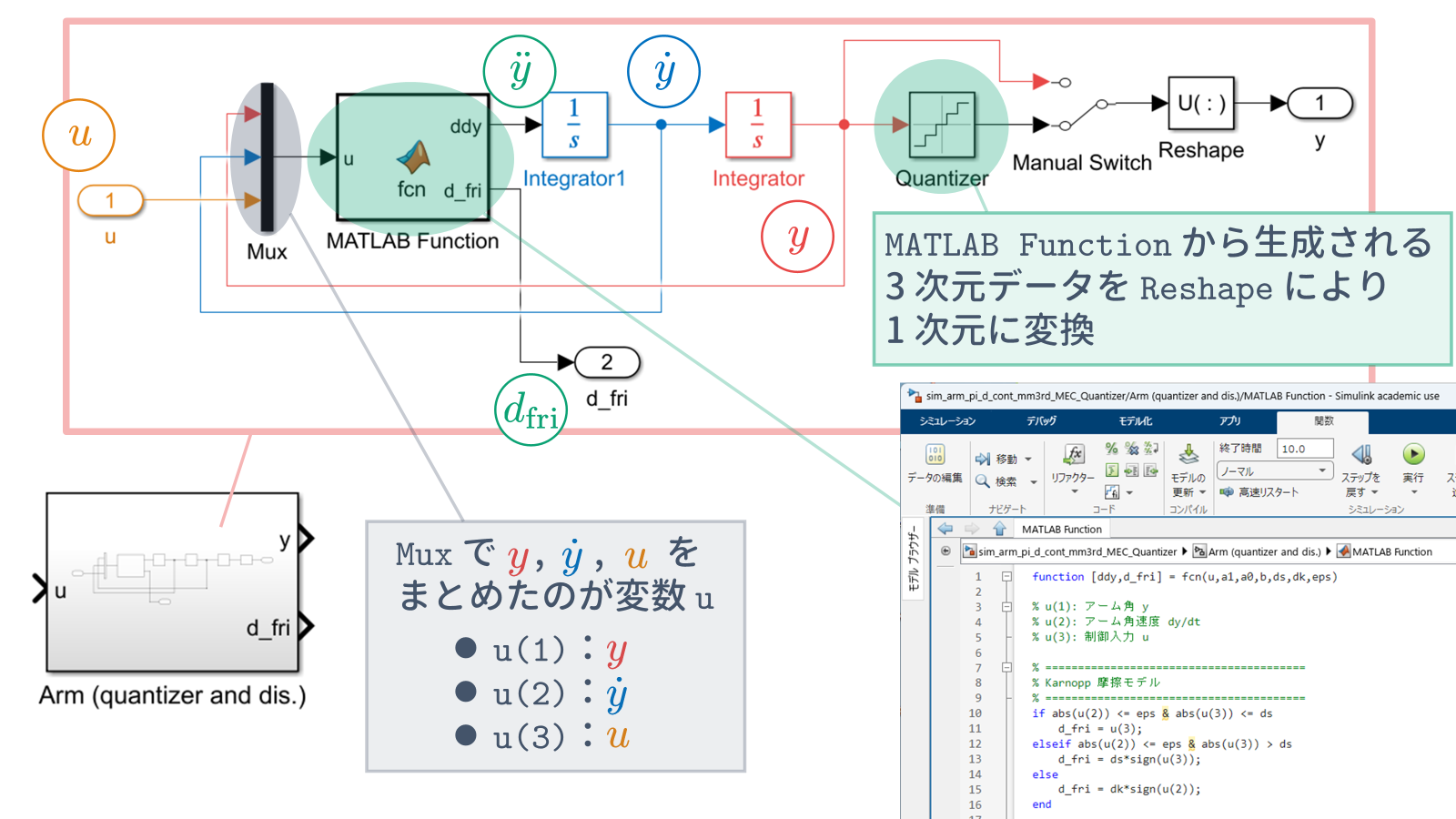
ブロック $\tt MATLAB\ Function$ は以下のように記述されています.非線形摩擦は Karnopp 摩擦モデルとしています.
function [ddy,d_fri] = fcn(u,a1,a0,b,ds,dk,eps)
% u(1): アーム角 y
% u(2): アーム角速度 dy/dt
% u(3): 制御入力 u
% ========================================
% Karnopp 摩擦モデル
% ========================================
if abs(u(2)) <= eps & abs(u(3)) <= ds
d_fri = u(3);
elseif abs(u(2)) <= eps & abs(u(3)) > ds
d_fri = ds*sign(u(3));
else
d_fri = dk*sign(u(2));
end
% ========================================
% スティックスリップ摩擦モデル
% ========================================
% if u(2) == 0 & abs(u(3)) <= dmax
% d_fri = u(3);
% elseif u(2) == 0 & abs(u(3)) > dmax
% d_fri = dmax*sign(u(3));
% else
% d_fri = dk*sign(u(2));
% end
% ========================================
% 非線形微分方程式
% ddy = b*(u - d_fri) - a0*sin(y) - a1*dy
% y :アーム角
% dy :アーム角速度
% ddy:アーム角加速度
% u :指令電圧
% d_fri:非線形摩擦
% ========================================
ddy = b*(u(3) - d_fri) - a0*sin(u(1)) - a1*u(2);
ブロック $\tt MATLAB\ Function$ の使い方に関しては,
が参考になります.
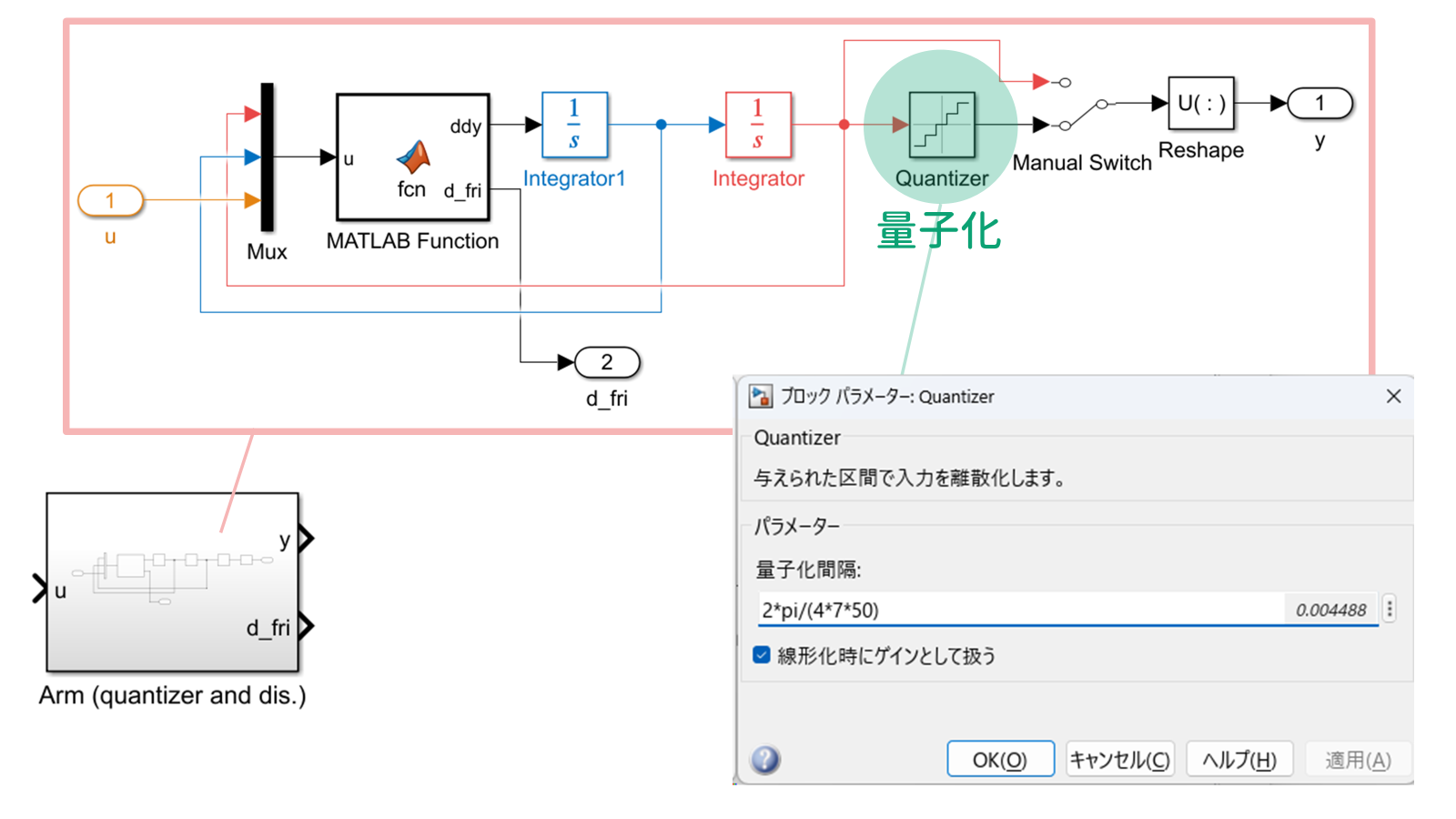
(b) エンコーダの量子化誤差
実験装置では,角度センサに磁気式ロータリエンコーダを使用しています.そこで,
- カウンタのモード 4 逓倍
- エンコーダの分解能 7 PPR
- ギヤの減速比 50:1
ですので,量子化サイズを
\begin{align}
\dfrac{2\pi}{4 \times 7 \times 50}
\end{align}
として角度信号を処理しています.
Simulink モデルでは,ブロック $\tt Quantizer$ により量子化を行っています.
なお,$\tt Manual\ Switch$ を上側にすることで,エンコーダの量子化を考慮しないようにすることもできます.
6.2 PI-D 制御系に MEC を付加したときの非線形シミュレーション
まず,配布する M ファイル
clear
format compact
ref = 60;
% ===================================================
% アーム系のパラメータ
% ===================================================
alpha = 1.1666e-02;
beta = 2.4771e-01;
gamma = 8.5001e-01;
b = 1/alpha;
a1 = beta/alpha;
a0 = gamma/alpha;
% -----------------------------------------
ds = 0.5; % 最大静止摩擦
dk = 0.25; % 動摩擦
eps = 0.005; % Karnopp 摩擦モデル
% ===================================================
% 部分的モデルマッチング法による PI-D コントローラ設計
% ===================================================
wm = 15;
% Butterworth
am2 = 2;
am1 = 2;
% binomial
% am2 = 3;
% am1 = 3;
% ITAE
% am2 = 1.75;
% am1 = 2.15;
% -----------------------------------------
gamma1 = am1/wm;
gamma2 = am2/wm^2;
gamma3 = 1/wm^3;
% -----------------------------------------
kI = a0/(b*gamma1);
kP = (1/b - gamma3*kI)/gamma2;
kD = gamma2*kI + (1/b)*(a0*kP/kI - a1);
fprintf('========================= \n')
fprintf('部分的モデルマッチング法 \n')
fprintf('wm = %5.4e\n',wm)
fprintf('am2 = %5.4e\n',am2)
fprintf('am1 = %5.4e\n',am1)
fprintf('~~~~~~~~~~~~~~~~~~~~~~~~~ \n')
fprintf('kI = %5.4e\n',kI)
fprintf('kP = %5.4e\n',kP)
fprintf('kD = %5.4e\n',kD)
% ===================================================
% MEC のゲイン(PI 型)
% ===================================================
kP2 = 50;
kI2 = 100;
fprintf('========================= \n')
fprintf('MEC による誤差補償器 \n')
fprintf('kI2 = %5.4e\n',kI2)
fprintf('kP2 = %5.4e\n',kP2)
% ===================================================
% 外乱オブザーバにおけるローパスフィルタ Gf
% ===================================================
s = tf('s');
sysP = b/(s^2 + a1*s + a0);
sysD = kP2 + kI2/s;
fprintf('========================= \n')
fprintf('ローパスフィルタ Gf \n')
sysGf = minreal(sysP*sysD/(1 + sysP*sysD))
fprintf('========================= \n')
を実行します.実行結果は
>> design_pi_d_cont_mm3rd_MEC
=========================
部分的モデルマッチング法
wm = 1.5000e+01
am2 = 2.0000e+00
am1 = 2.0000e+00
~~~~~~~~~~~~~~~~~~~~~~~~~
kI = 6.3751e+00
kP = 1.0999e+00
kD = -4.4386e-02
=========================
MEC による誤差補償器
kI2 = 1.0000e+02
kP2 = 5.0000e+01
=========================
ローパスフィルタ Gf
sysGf =
4286 s + 8572
-------------------------------
s^3 + 21.23 s^2 + 4359 s + 8572
連続時間の伝達関数です。
モデル プロパティ
=========================
となります.
つぎに,配布する Simulink モデル
を開きます.ここで,Simulink モデルの右側のブロック $\tt MATLAB\ Function$ はシミュレーション結果をアニメーション表示するためのものであり,以下のように記述されています.
function fcn(t,y,r)
% if mod(t*1000,25) == 0
if mod(t*1000,100) == 0
L = 0.4;
figure(10); clf;
axis off
set(gcf,'Color','w')
plot([-0.55 -0.55 0.55 0.55 -0.55],[-0.55 0.55 0.55 -0.55 -0.55],'Color',[1 1 1],'LineWidth',2)
hold on
axis('square')
axis([-0.55 0.55 -0.55 0.55]);
set(gca,'FontSize',12,'FontName','Arial')
set(gca,'XTick',[]) % 横軸の目盛
set(gca,'XTickLabel',[]) % 横軸の目盛のラベル
set(gca,'YTick',[]) % 縦軸の目盛
set(gca,'YTickLabel',[]) % 縦軸の目盛のラベル
% アーム取り付け台
plot([-0.05 0.05],[0 0],'Color',[0.8 0.8 0.8],'LineWidth',25)
% 足
plot([-0.125 -0.125],[-0.1 -0.015],'k','LineWidth',4)
plot([ 0.125 0.125],[-0.1 -0.015],'k','LineWidth',4)
plot([-0.15 -0.1],[-0.095 -0.095],'k','LineWidth',4)
plot([ 0.15 0.1],[-0.095 -0.095],'k','LineWidth',4)
% 台
plot([-0.175 0.175],[-0.06 -0.06],'Color',[0.6 0.6 0.6],'LineWidth',5)
% 地面
plot([-0.55 0.55],[-0.325 -0.325],'Color',[205 161 111]/255,'LineWidth',105)
% アーム
plot([0 -L*sin(y)],[0 -L*cos(y)],'Color',[0 112 192]/255,'LineWidth',12.5);
% 初期値,目標値
plot([0 0],[0 -2*L],'--','Color',[232 71 70]/255)
plot([0 -2*L*sin(r)],[0 -2*L*cos(r)],'--','Color',[232 71 70]/255)
% 時間表示
text(0.5,0.5,sprintf('%2.1f [s]',t),'FontSize',12,'FontName','Arial')
% 目標値表示
text(0.5,0.55,sprintf('r = %4.0f [deg]',r*180/pi),'FontSize',12,'FontName','Arial')
hold off
end
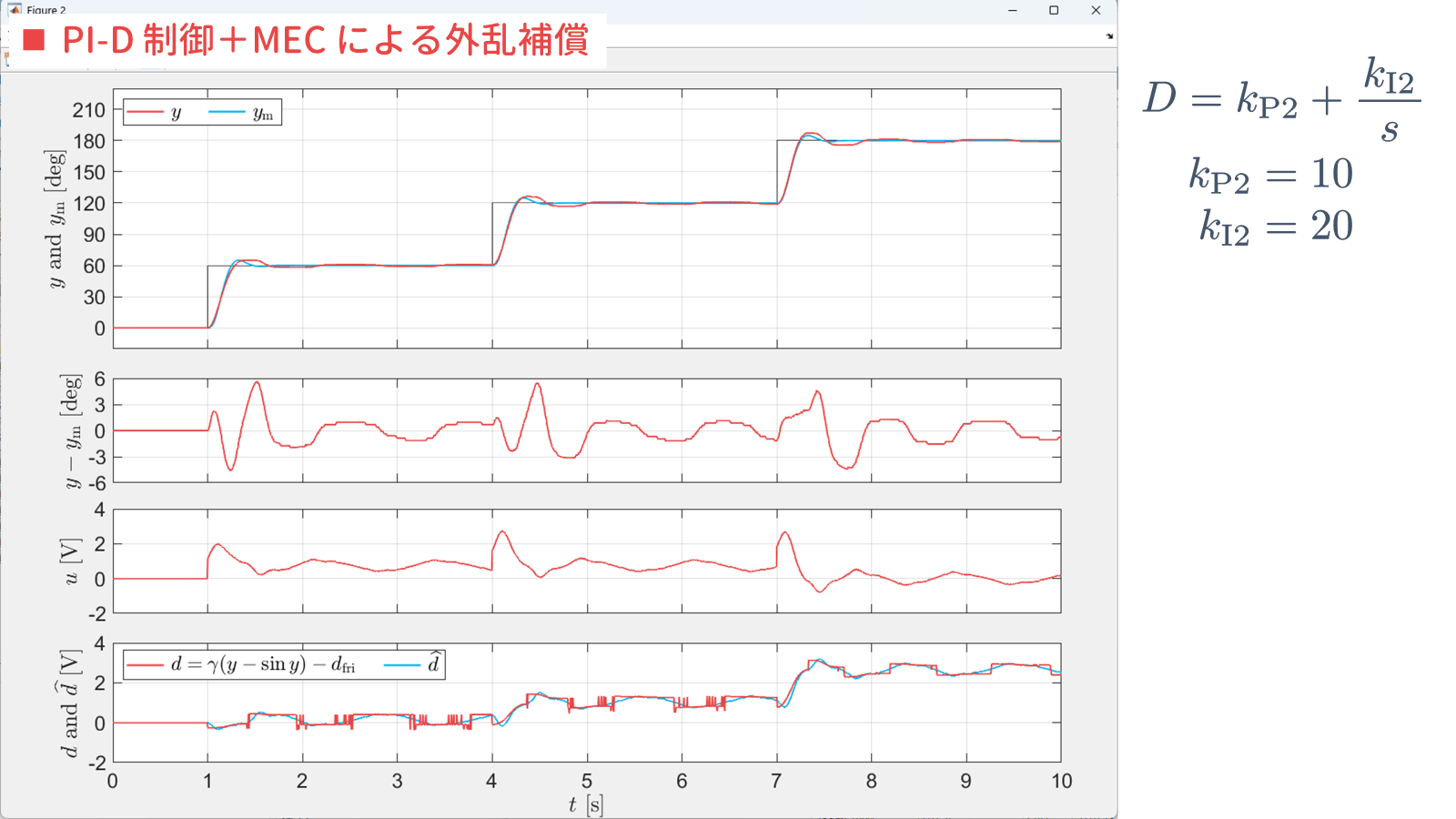
(a) 外乱補償を行わないときの非線形シミュレーション
外乱補償を行わないときの非線形シミュレーションを行うために,ブロック $\tt Manual\ Switch$ をダブルクリックして,上側($\tt Constant: 0$)に切り替えます.そして,シミュレーションを開始すると,以下のようになり,振動的な結果となります.
また,シミュレーション結果を描画するために,配布する M ファイル
close all
% -------------------------------------
figure(2)
set(gcf,'Position',[100 100 1200 800]) % [x0 y0 width height]
% グラフの配置 [left bottom width height]
position1 = [0.1 0.63 0.85 0.35]; % y
position2 = [0.1 0.45 0.85 0.14]; % y - ym
position3 = [0.1 0.275 0.85 0.14]; % u
position4 = [0.1 0.075 0.85 0.16]; % d_hat
% ***************
subplot('Position',position1)
plot([0 1 1 4 4 7 7 10],ref*[0 0 1 1 2 2 3 3],'k')
hold on
p2 = plot(t,rad2deg(ym),'LineWidth',1.5,'Color','#00B0F0');
p1 = plot(t,rad2deg(y), 'LineWidth',1.5,'Color','#E84746');
hold off
set(gca,'fontname','arial','FontSize',16)
ylabel('$y$ and ${y}_{\rm m}$ [deg]', 'interpreter','latex','FontSize',18)
ylim([-20 230])
set(gca,'YTick',0:30:300)
xlim([0 10])
set(gca,'XTick',0:1:10)
set(gca,'XTickLabel',{''})
grid on
legend([p1 p2],...
{'\hskip2pt $y\quad$',
'\hskip2pt ${y}_{\rm m}\hskip2pt$'}, ...
'interpreter','latex','FontSize',16,...
'Location','NorthWest','NumColumns',2)
% ***************
subplot('Position',position3) % [left bottom width height]
plot(t,u,'LineWidth',1.5,'Color','#E84746')
set(gca,'fontname','arial','FontSize',16)
ylabel('$u$ [V]', 'interpreter','latex','FontSize',18)
ylim([-2 4])
set(gca,'YTick',-2:2:4)
xlim([0 10])
set(gca,'XTickLabel',{''})
grid on
% ***************
subplot('Position',position2) % [left bottom width height]
plot(t, rad2deg(y-ym), 'LineWidth',1.5,'Color','#E84746');
set(gca,'fontname','arial','FontSize',16)
ylabel('$y - {y}_{\rm m}$ [deg]', 'interpreter','latex','FontSize',18)
ylim([-6 6])
set(gca,'YTick',-6:3:6)
set(gca,'XTick',0:1:10)
set(gca,'XTickLabel',{''})
grid on
% ***************
subplot('Position',position4) % [left bottom width height]
p3 = plot(t,d_hat,'LineWidth',1.5,'Color','#00B0F0');
hold on
p4 = plot(t, gamma*(y-sin(y)) - d_fri, 'LineWidth',1.5,'Color','#E84746');
hold off
set(gca,'fontname','arial','FontSize',16)
xlabel('$t$ [s]', 'interpreter', 'latex','FontSize',18)
ylabel('$d$ and $\widehat{d}$ [V]', 'interpreter', 'latex','FontSize',18)
ylim([-2 4])
set(gca,'YTick',-10:2:10)
xlim([0 10])
grid on
legend([p4 p3],...
{'\hskip2pt $d = \gamma(y - \sin{y}) - d_{\rm fri}\quad$',
'\hskip2pt $\widehat{d}\hskip2pt$'}, ...
'interpreter','latex','FontSize',16,...
'Location','NorthWest','NumColumns',2)
を実行します.M ファイル "plot_data.m" の実行結果を以下に示します.
(b) MEC により外乱補償を行ったときの非線形シミュレーション
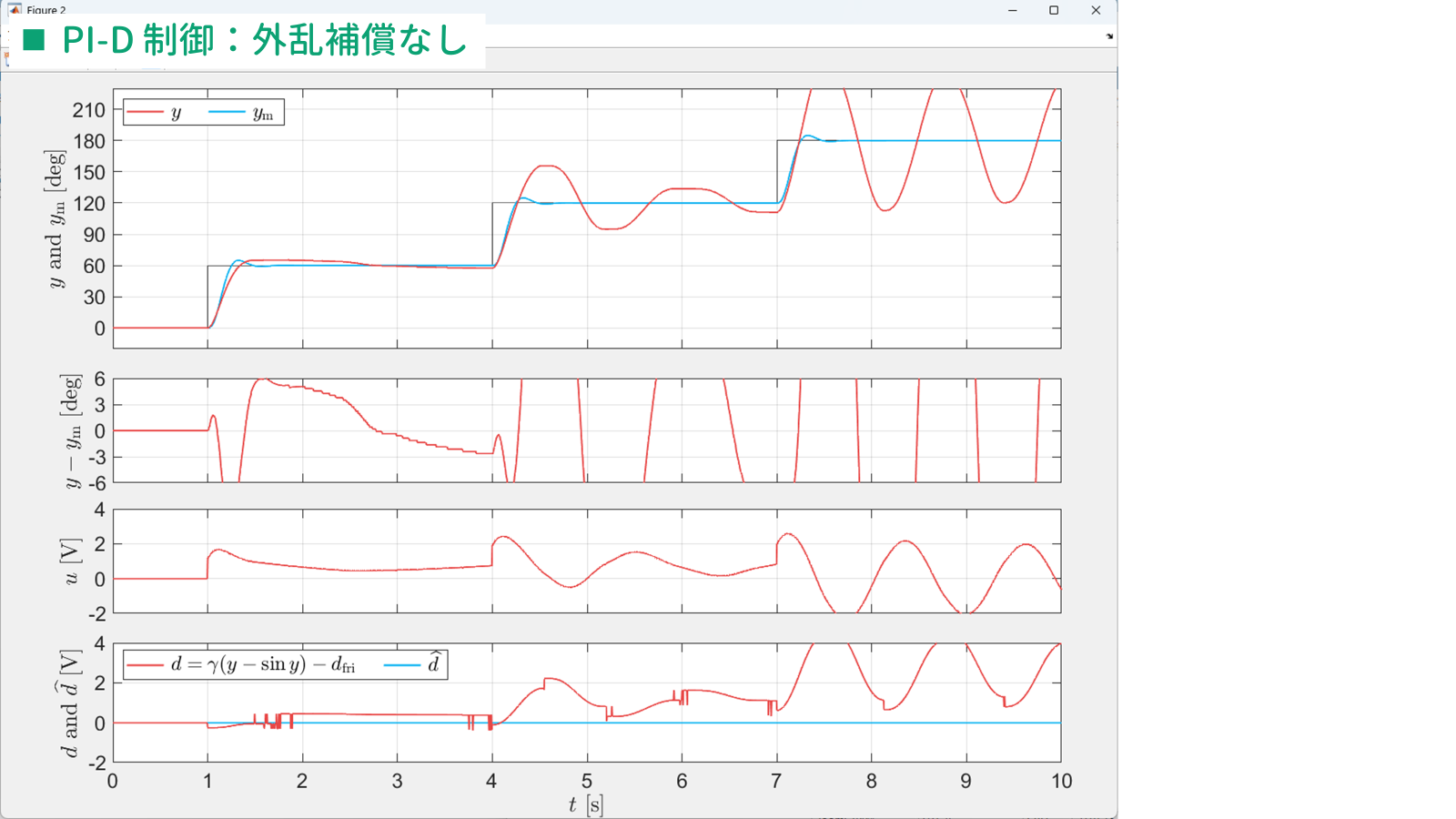
外乱補償を行ったときの非線形シミュレーションを行うために,ブロック $\tt Manual\ Switch$ をダブルクリックして,下側($k_{\rm P2} = 50$, $k_{\rm I2} = 100$ とした誤差補償器 $D$)に切り替えます.そして,シミュレーションを開始すると,以下のようになります.
また,シミュレーション結果を描画するために,配布する M ファイル "plot_data.m" を実行すると,以下のグラフが表示されます.
これらの結果より,MEC により適切に外乱が推定されており,うまく外乱を除去できていることが確認できます.また,誤差補償器を PI 型としているため,量子化誤差に対して過敏に反応しておらず,チャタリングを生じていないことが確認できます.実際に実験した結果を以下に示します.
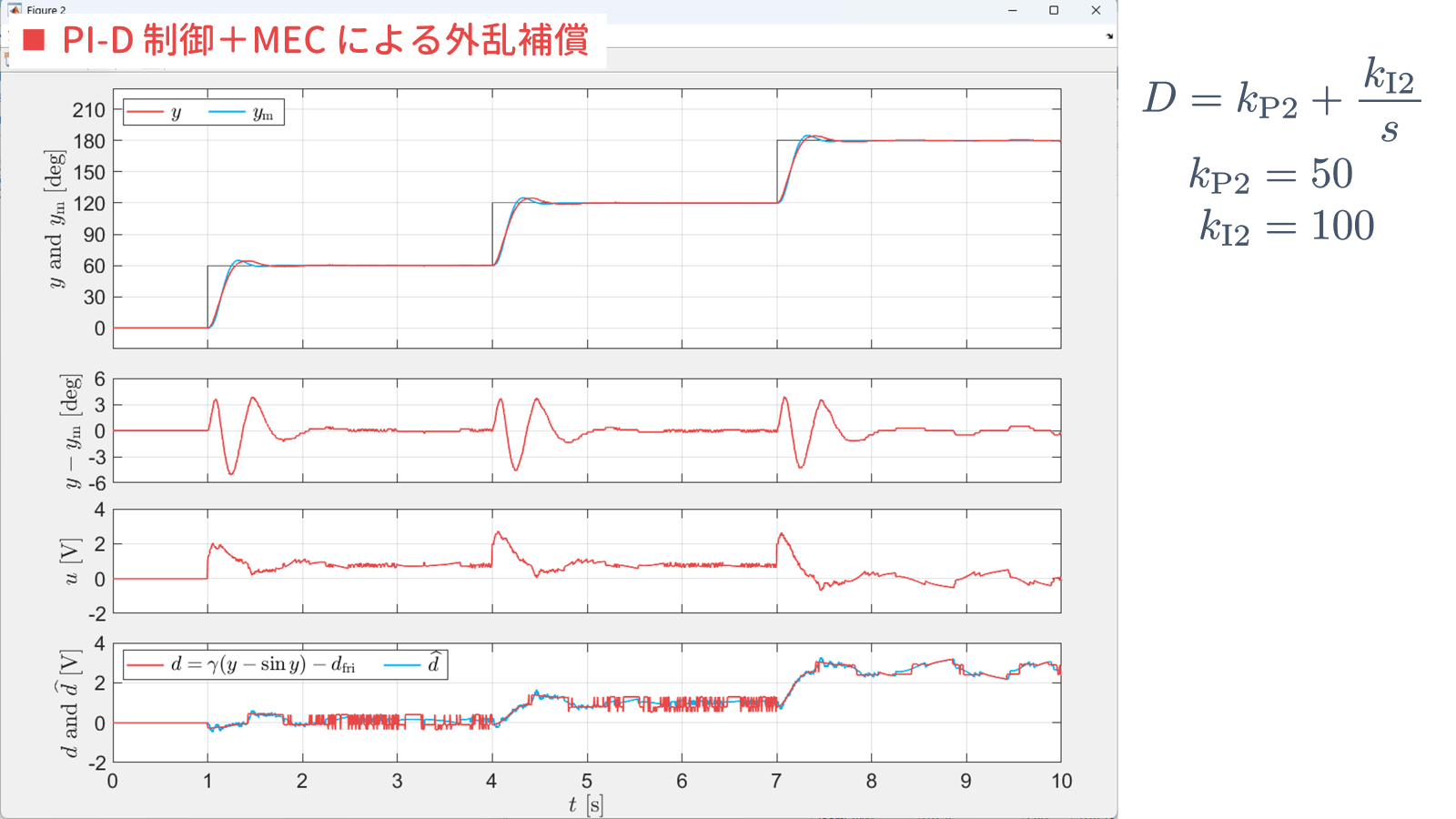
一方で,誤差補償器 $D$ のゲインを $k_{\rm P2} = 10$, $k_{\rm I2} = 20$ のように小さくすると,すなわち,M ファイル "design_pi_d_cont_mm3rd_MEC.m" の 63, 64 行目を,
kP2 = 10;
kI2 = 20;
のように書き換えて実行すると,
>> design_pi_d_cont_mm3rd_MEC
=========================
部分的モデルマッチング法
wm = 1.5000e+01
am2 = 2.0000e+00
am1 = 2.0000e+00
-------------------------
kI = 6.3751e+00
kP = 1.0999e+00
kD = -4.4386e-02
=========================
MEC による誤差補償器
kI2 = 2.0000e+01
kP2 = 1.0000e+01
=========================
ローパスフィルタ Gf
sysGf =
857.2 s + 1714
--------------------------------
s^3 + 21.23 s^2 + 930.1 s + 1714
連続時間の伝達関数です。
モデル プロパティ
=========================
となります.また,非線形シミュレーションを行うと以下の結果が得られ,追従性が不十分であることを確認できます.
6.3 PI-D 制御系に外乱オブザーバを付加したときの非線形シミュレーション
配布する M ファイル
clear
format compact
ref = 60;
% ===================================================
% アーム系のパラメータ
% ===================================================
alpha = 1.1666e-02;
beta = 2.4771e-01;
gamma = 8.5001e-01;
b = 1/alpha;
a1 = beta/alpha;
a0 = gamma/alpha;
% -----------------------------------------
ds = 0.5; % 最大静止摩擦
dk = 0.25; % 動摩擦
eps = 0.005; % Karnopp 摩擦モデル
% ===================================================
% 部分的モデルマッチング法による PI-D コントローラ設計
% ===================================================
wm = 15;
% Butterworth
am2 = 2;
am1 = 2;
% binomial
% am2 = 3;
% am1 = 3;
% ITAE
% am2 = 1.75;
% am1 = 2.15;
% -----------------------------------------
gamma1 = am1/wm;
gamma2 = am2/wm^2;
gamma3 = 1/wm^3;
% -----------------------------------------
kI = a0/(b*gamma1);
kP = (1/b - gamma3*kI)/gamma2;
kD = gamma2*kI + (1/b)*(a0*kP/kI - a1);
fprintf('========================= \n')
fprintf('部分的モデルマッチング法 \n')
fprintf('wm = %5.4e\n',wm)
fprintf('am2 = %5.4e\n',am2)
fprintf('am1 = %5.4e\n',am1)
fprintf('~~~~~~~~~~~~~~~~~~~~~~~~~ \n')
fprintf('kI = %5.4e\n',kI)
fprintf('kP = %5.4e\n',kP)
fprintf('kD = %5.4e\n',kD)
% ===================================================
% 外乱オブザーバによる設計
% ===================================================
wc = 250; % 2 次のバターワースフィルタ
fprintf('========================= \n')
fprintf('2次のバターワースフィルタ \n')
fprintf('wc = %5.4e\n',wc)
fprintf('~~~~~~~~~~~~~~~~~~~~~~~~~ \n')
s = tf('s');
sysGf = wc^2/(s^2 + sqrt(2)*wc*s + wc^2)
fprintf('ノミナルモデル Pn \n')
sysPn = b/(s^2 + a1*s + a0)
sysGf_invPn = sysGf/sysPn;
sysGf_invPn = tf(zpk(sysGf_invPn));
% -----------------------------------------
Tf2 = 1/(sqrt(2)*wc);
kI2 = wc/(sqrt(2)*b)*a0;
kP2 = wc/(sqrt(2)*b)*(a1 - a0/(sqrt(2)*b));
kD2 = wc/(sqrt(2)*b)*(1 - 1/(sqrt(2)*b)*(a1 - a0/(sqrt(2)*b)));
fprintf('========================= \n')
fprintf('外乱オブザーバによる誤差補償器 \n')
fprintf('wc = %5.4e\n',wc)
fprintf('~~~~~~~~~~~~~~~~~~~~~~~~~ \n')
fprintf('Tf2 = %5.4e\n',Tf2)
fprintf('kI2 = %5.4e\n',kI2)
fprintf('kP2 = %5.4e\n',kP2)
fprintf('kD2 = %5.4e\n',kD2)
fprintf('========================= \n')
を実行します.この M ファイルの実行結果は以下のようになります.
>> design_pi_d_cont_mm3rd_DOB
~~~~~~~~~~~~~~~~~~~~~~~~~
部分的モデルマッチング法
wm = 1.5000e+01
am2 = 2.0000e+00
am1 = 2.0000e+00
~~~~~~~~~~~~~~~~~~~~~~~~~
kI = 6.3751e+00
kP = 1.0999e+00
kD = -4.4386e-02
=========================
2次のバターワースフィルタ
wc = 2.5000e+02
~~~~~~~~~~~~~~~~~~~~~~~~~
sysGf =
62500
---------------------
s^2 + 353.6 s + 62500
連続時間の伝達関数です。
モデル プロパティ
~~~~~~~~~~~~~~~~~~~~~~~~~
ノミナルモデル Pn
sysPn =
85.72
---------------------
s^2 + 21.23 s + 72.86
連続時間の伝達関数です。
モデル プロパティ
=========================
外乱オブザーバによる誤差補償器
wc = 2.5000e+02
~~~~~~~~~~~~~~~~~~~~~~~~~
Tf2 = 2.8284e-03
kI2 = 1.5026e+02
kP2 = 4.2550e+01
kD2 = 1.7113e+00
=========================
つぎに,配布する Simulink モデル
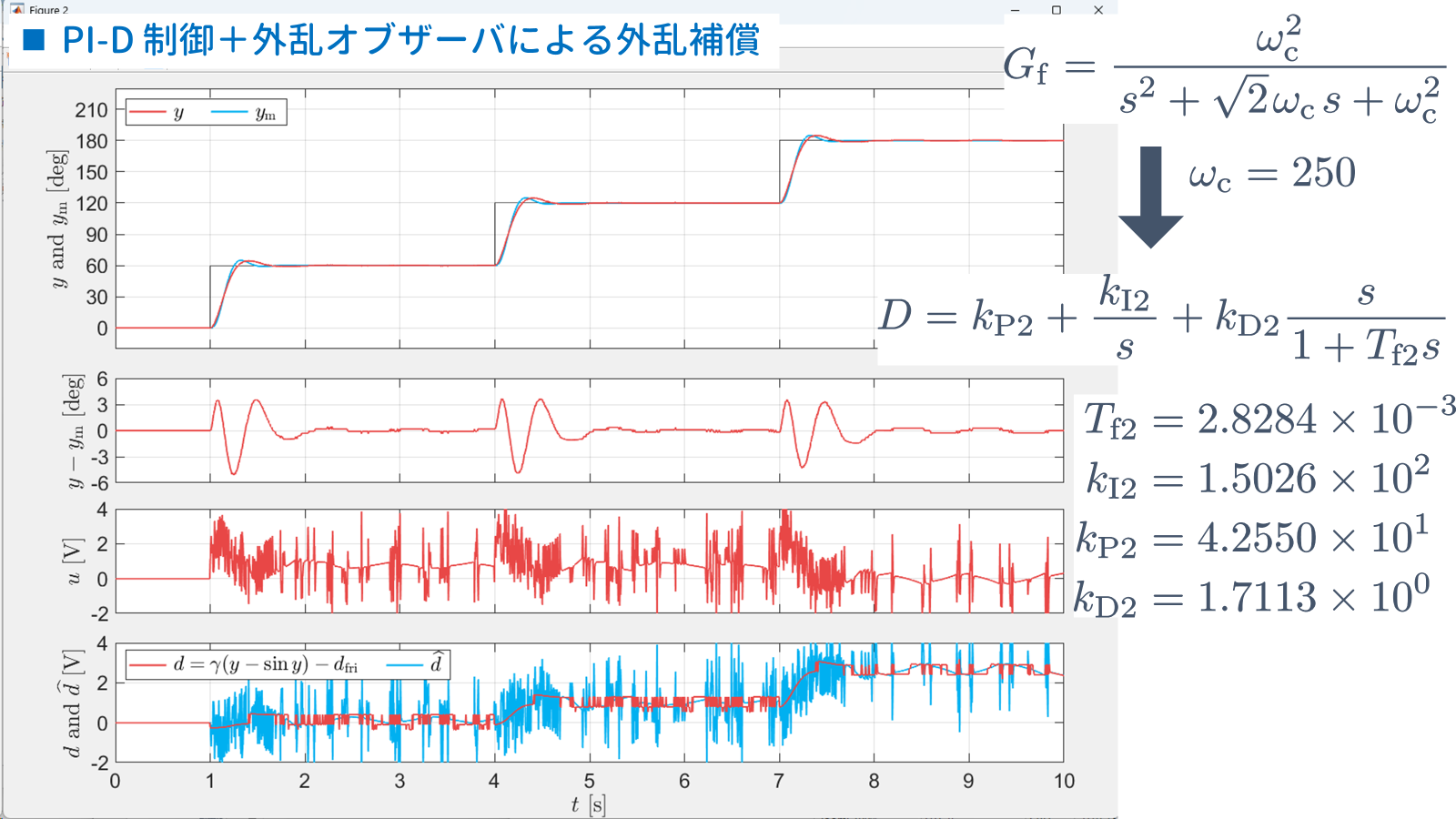
を開き,ブロック $\tt Manual\ Switch$ が下側であることを確認します.そして,実行を開始すると,以下の結果が表示されます.
また,シミュレーション結果を描画するために,配布する M ファイル "plot_data.m" を実行すると,以下のグラフが表示されます.
これらの結果より,外乱オブザーバにより,外乱を除去していることが確認できます.しかし,MEC と比べると,量子化誤差の影響が大きく,外乱の推定値 $\widehat{d}$ に高周波成分を多く含みます.その結果,制御入力 $u$ にも高周波成分が多く含まれますので,実際に実験を行うと,チャタリングが問題となります.
この動画より,チャタリングをしている音が確認できます.
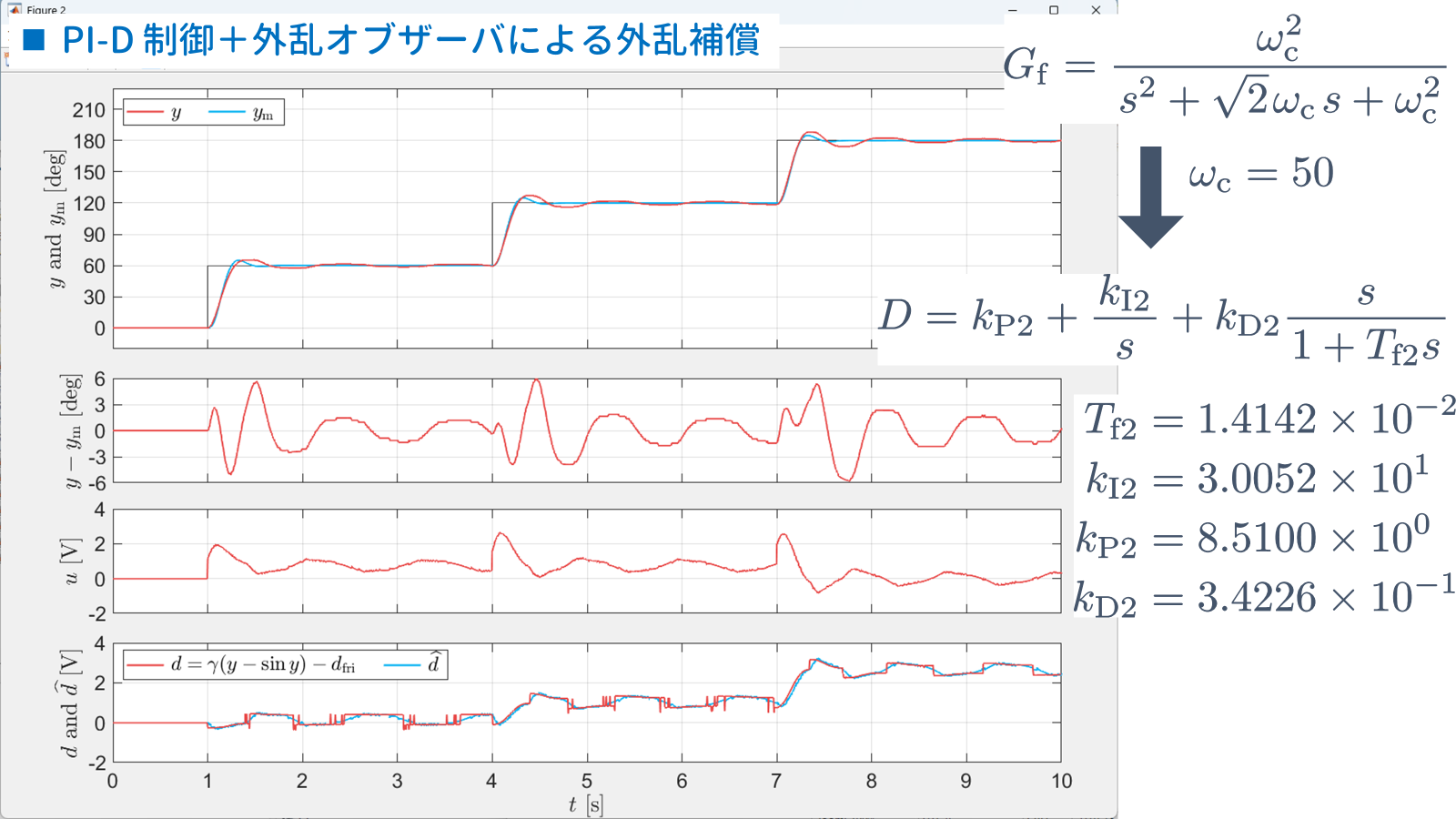
チャタリングに対処するためには,2 次のバターワースフィルタのカットオフ角周波数 $\omega_{\rm c}$ を小さくする必要があります.たとえば,$\omega_{\rm c} = 50$ のように小さくすると,すなわち,M ファイル "design_pi_d_cont_mm3rd_DOB.m" の 63 行目を,
wc = 50;
のように書き換えて実行すると,
>> design_pi_d_cont_mm3rd_DOB
~~~~~~~~~~~~~~~~~~~~~~~~~
部分的モデルマッチング法
wm = 1.5000e+01
am2 = 2.0000e+00
am1 = 2.0000e+00
~~~~~~~~~~~~~~~~~~~~~~~~~
kI = 6.3751e+00
kP = 1.0999e+00
kD = -4.4386e-02
=========================
2次のバターワースフィルタ
wc = 5.0000e+01
~~~~~~~~~~~~~~~~~~~~~~~~~
sysGf =
2500
--------------------
s^2 + 70.71 s + 2500
連続時間の伝達関数です。
モデル プロパティ
~~~~~~~~~~~~~~~~~~~~~~~~~
ノミナルモデル Pn
sysPn =
85.72
---------------------
s^2 + 21.23 s + 72.86
連続時間の伝達関数です。
モデル プロパティ
=========================
外乱オブザーバによる誤差補償器
wc = 5.0000e+01
~~~~~~~~~~~~~~~~~~~~~~~~~
Tf2 = 1.4142e-02
kI2 = 3.0052e+01
kP2 = 8.5100e+00
kD2 = 3.4226e-01
=========================
となります.また,非線形シミュレーションを行うと以下の結果が得られ,追従性が不十分であることを確認できます.
となります.このとき,チャタリングは軽減されますが,追従性は劣化していることが確認できます.
7. おわりに
今回もだらだらと書いてしまいました...
いろいろと思い違いしているかもしれませんので,お気づきのことがあればご指摘ください.