1. はじめに
「制御工学」で学習する 2 次遅れ系
\begin{align}
y(s) = P(s)u(s),\
P(s) = \dfrac{K{\omega}_{\rm n}^{2}}
{s^2 + 2\zeta{\omega}_{\rm n}s + {\omega}_{\rm n}^{2}}
\tag{1}
\end{align}
を考えます.ここで,
- $\zeta > 0$:減衰係数 $\cdots\cdots$ 安定度のパラメータ
- ${\omega}_{\rm n} > 0$:固有角周波数 $\cdots\cdots$ 速応性のパラメータ
- $K \neq 0$:ゲイン $\cdots\cdots$ 定常特性のパラメータ
です.また,信号 $u(t)$, $y(t)$ のラプラス変換を $u(s) = {\cal L}\bigl[u(t)\bigr]$, $y(s) = {\cal L}\bigl[y(t)\bigr]$ のように小文字で記述しています.
本記事では,$\zeta$, ${\omega}_{\rm n}$, $K$ を変化させたときに,$(1)$ 式の単位ステップ応答 $y(t)$ がどのように変化するのかを,Simulink で確認する例を説明します.
なお,Simulink モデルは GitHub で公開しています(R2023a, R2022a, R2020a 用).
2. 2 次遅れ系の Simulink での表現
単に,Simulink を利用して 2 次遅れ系のステップ応答を描画するのであれば,Simulink ブロック "$\tt Transfer\ Fcn$" を利用して
のようにすれば良いです.しかし,今回は,シミュレーションを行っている最中に $\zeta$, ${\omega}_{\rm n}$, $K$ の値を変化させて,その振る舞いの変化を確認することを目的としているために,
- 2 次遅れ系を微分方程式で書き換え,Simulink ブロック "$\tt Fcn$" で記述する
- Simulink ブロック "$\tt Fcn$" で微分方程式を記述する際にパラメータ $\zeta$, ${\omega}_{\rm n}$, $K$ を信号 $u(t)$, $y(t)$, $\dot{y}(t)$ と同様に変数として扱う
というアプローチを考えます.まぁ,大したことを行うわけではありません.
2 次遅れ系 $(1)$ 式を書き換えると,
\begin{align*}
&
(s^2 + 2\zeta{\omega}_{\rm n}s + {\omega}_{\rm n}^{2})y(s)
= K{\omega}_{\rm n}^{2}u(s)
\\
&\quad \Longrightarrow \quad
s^2y(s)
+ 2\zeta{\omega}_{\rm n}sy(s)
+ {\omega}_{\rm n}^{2}y(s)
= K{\omega}_{\rm n}^{2}u(s)
\tag{2}
\end{align*}
なので,$(1)$ 式は 2 階の線形微分方程式
\begin{align*}
&
\ddot{y}(t)
+ 2\zeta{\omega}_{\rm n}\dot{y}(t)
+ {\omega}_{\rm n}^{2}y(t)
= K{\omega}_{\rm n}^{2}u(t)
\\
&\quad \Longrightarrow \quad
\ddot{y}(t)
= K{\omega}_{\rm n}^{2}u(t)
- 2\zeta{\omega}_{\rm n}\dot{y}(t)
- {\omega}_{\rm n}^{2}y(t)
\tag{3}
\end{align*}
のように記述できます.そこで,Simulink ブロック "$\tt Fcn$" を利用して $(3)$ 式を表現します."$\tt Fcn$" の使い方については
で詳しく説明しています(R2020b から R2022b では "$\tt Fcn$" を Simulink ライブラリブラウザからは検索できませんので,上記の記事を参照して simulink3 から "$\tt Fcn$" を移動してください).
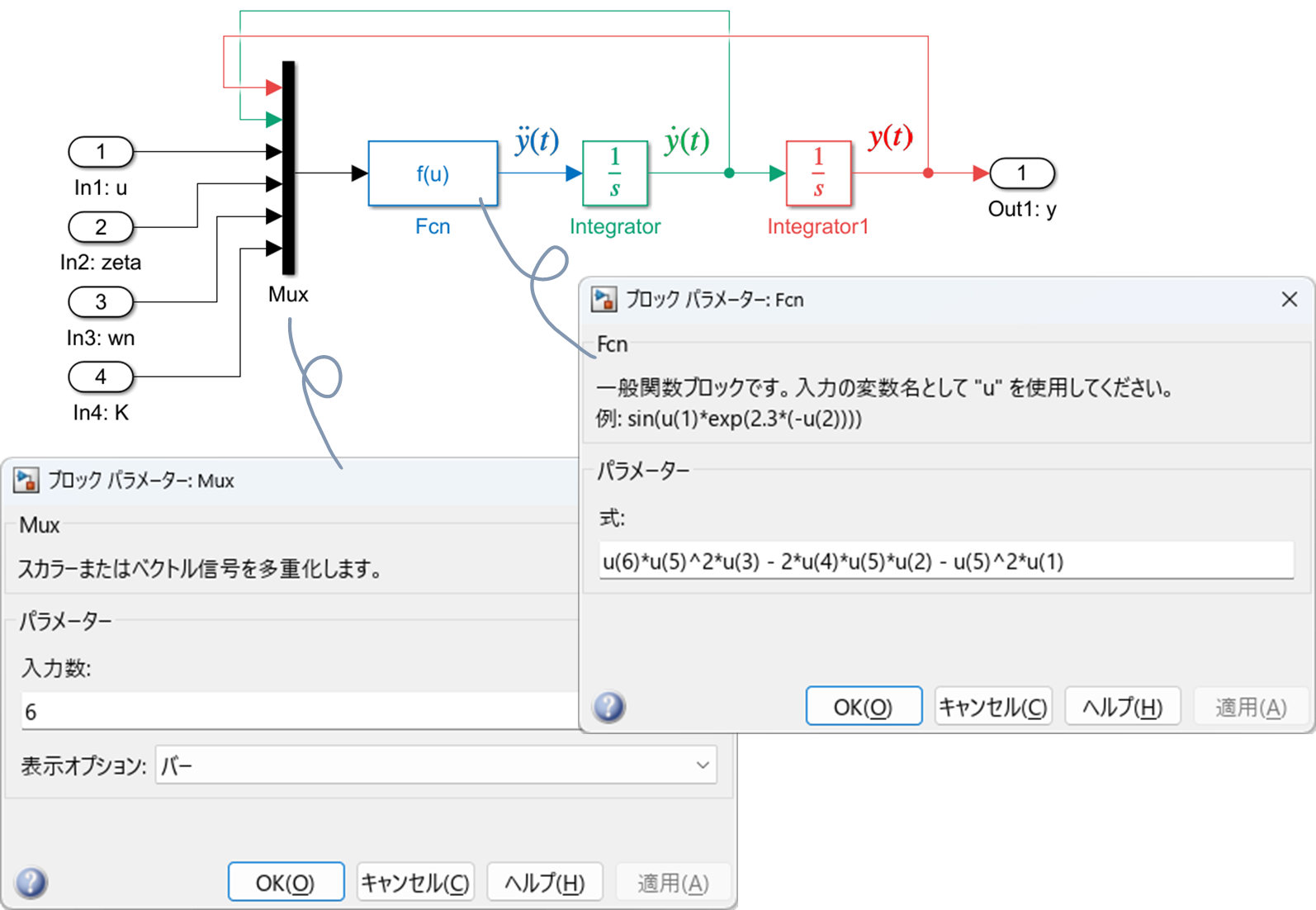
さて,"$\tt Subsystem$" の中に以下のように Simulink ブロックを配置し,パラメータや名前を設定した上で結線します.
"$\tt Fcn$" の入力は "$\tt Mux$" でベクトル化された信号であり,それぞれ
- $\tt u(1)$:$y(t)$
- $\tt u(2)$:$\dot{y}(t)$
- $\tt u(3)$:$u(t)$
- $\tt u(4)$:$\zeta$
- $\tt u(5)$:${\omega}_{\rm n}$
- $\tt u(6)$:$K$
を意味しています.そして,これらを用いて $(3)$ 式の右辺
\begin{align*}
K{\omega}_{\rm n}^{2}u(t)
- 2\zeta{\omega}_{\rm n}\dot{y}(t)
- {\omega}_{\rm n}^{2}y(t)
\end{align*}
を "$\tt Fcn$" では
\begin{align*}
\tt{
u(6)*u(5)^2*u(3) - 2*u(4)*u(5)*u(2) - u(5)^2*u(1)
}
\end{align*}
のように表現しています.したがって,"$\tt Fcn$" の出力は $\ddot{y}(t)$ となりますので,"$\tt Integrator$" を利用してこれを 1 回積分すると $\dot{y}(t)$,2 回積分すると $y(t)$ が得られます.これらをフィードバックして "$\tt Mux$" に入力しています.
以上で,2 次遅れ系を Simulink で表現することができました.
3. Simulink モデル
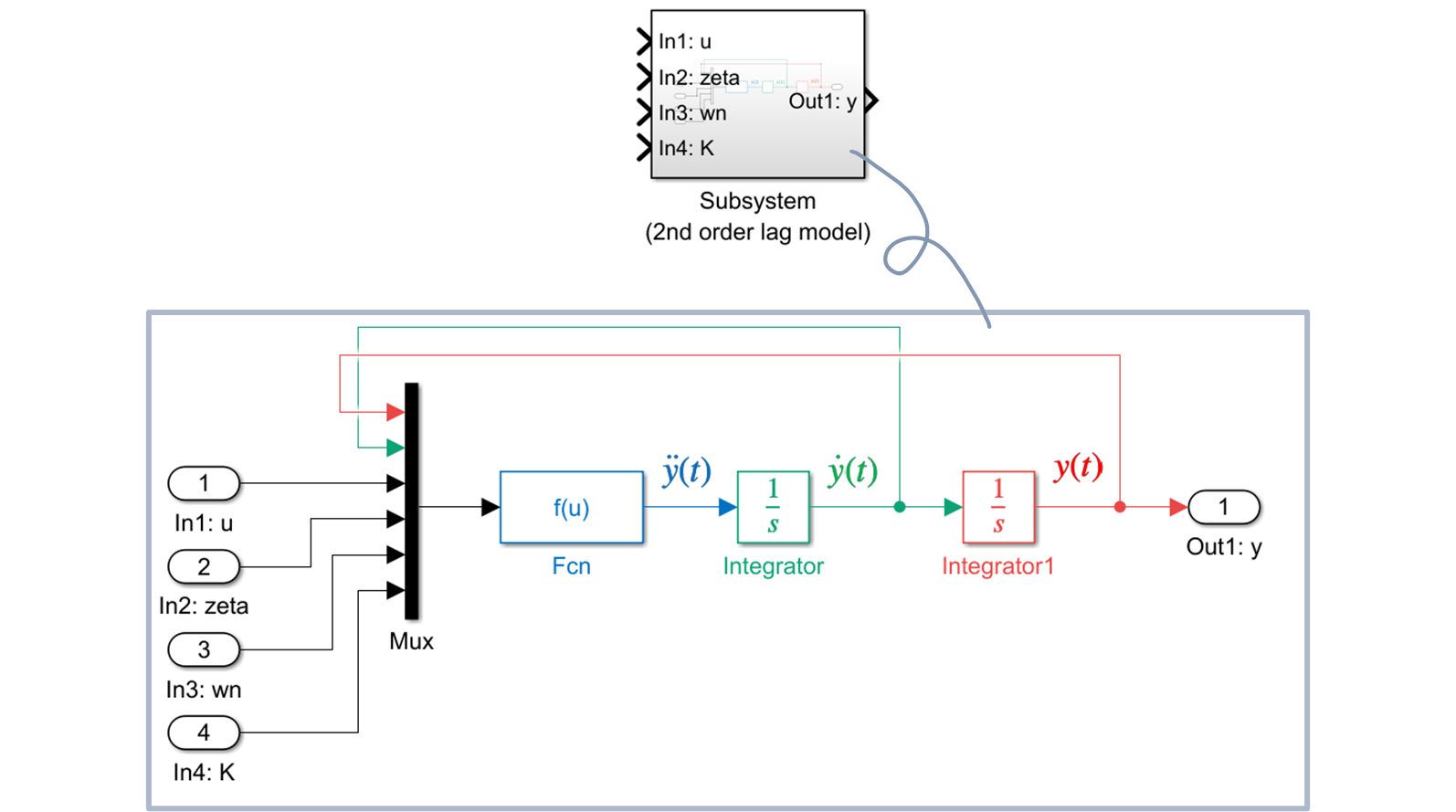
3.1 完成した Simulink モデル!!
配布する Simulink モデル "step_2nd_system.slx" を以下に示します.
3.2 Simulink ブロック の設定
3.2.1 Scope の設定
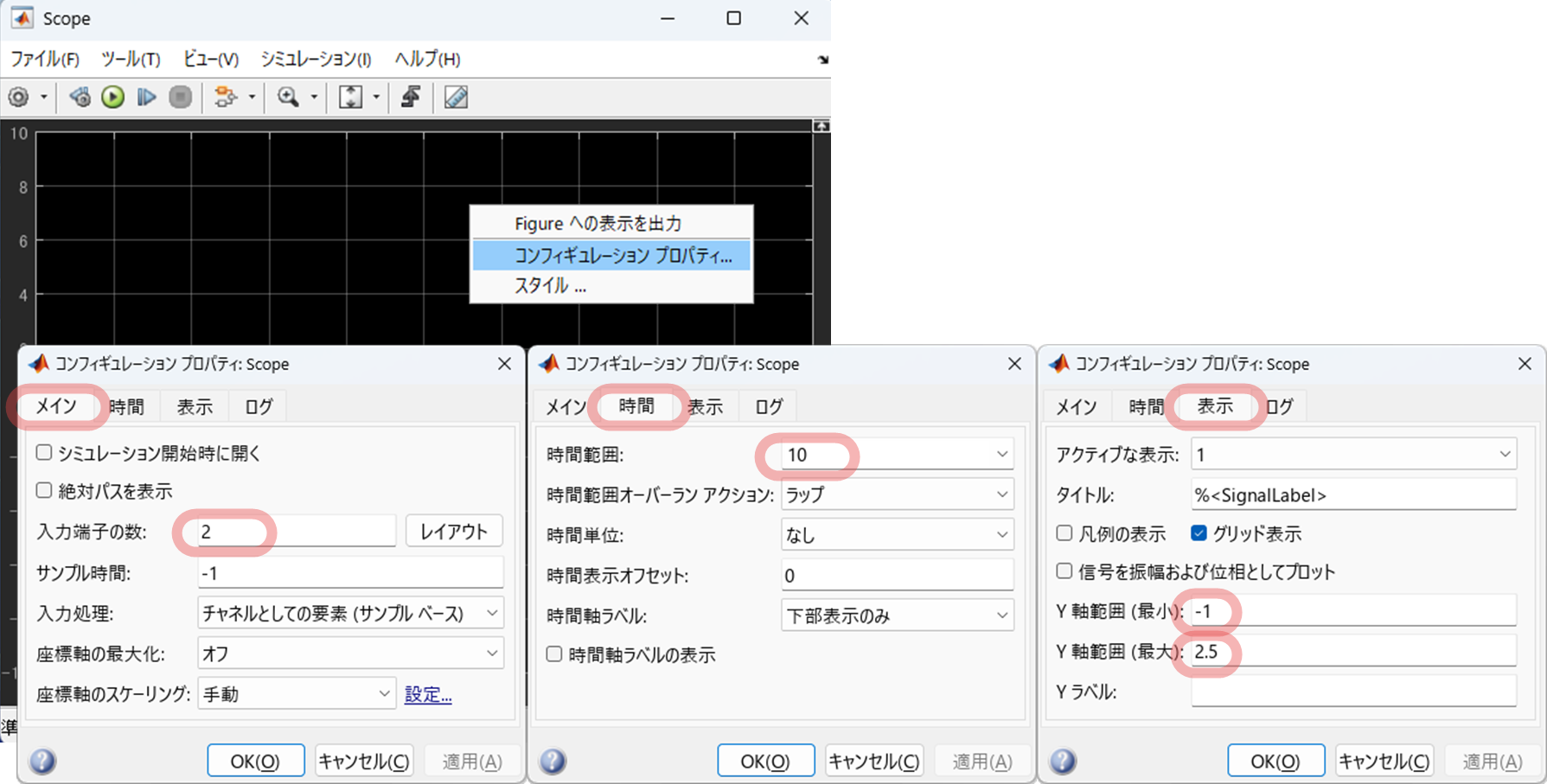
シミュレーションを行っている間,リアルタイムで信号を表示するために "$\tt Scope$" を利用します."$\tt Scope$" をダブルクリックするとウィンドウが起動しますので,マウスを右クリックすることで,コンフィギュレーションプロパティを
のように設定します.これにより,入力信号 $u(t)$ と出力信号 $y(t)$ を同じウィンドウに 10 秒ごとにリフレッシュしながら表示できるようになります.また,縦軸の範囲を $-1$ から $2.5$ に設定しています.
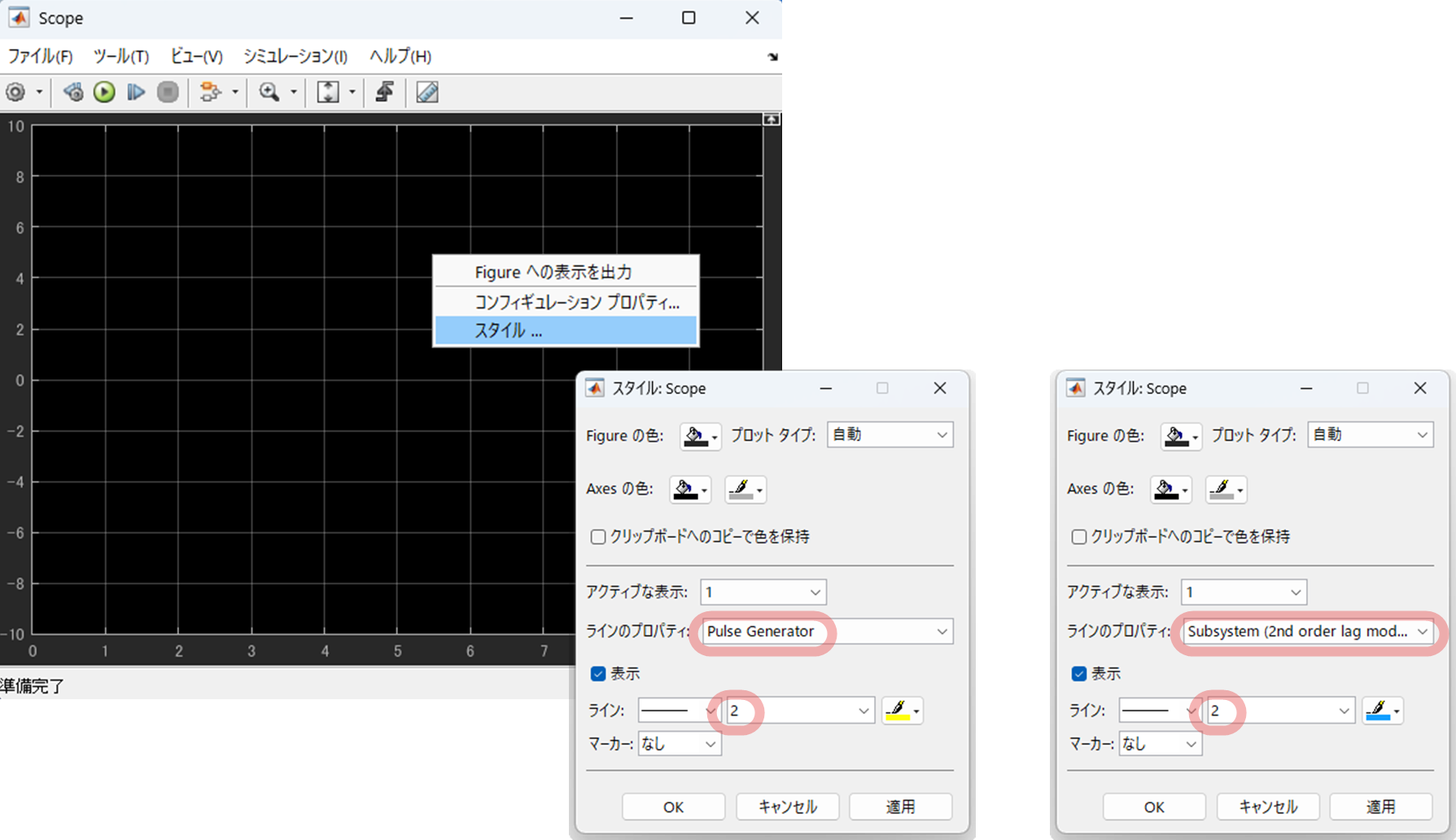
同様に,スタイルを
とし,入力信号 $u(t)$ と出力信号 $y(t)$ の描画の線の太さや色を設定しています.
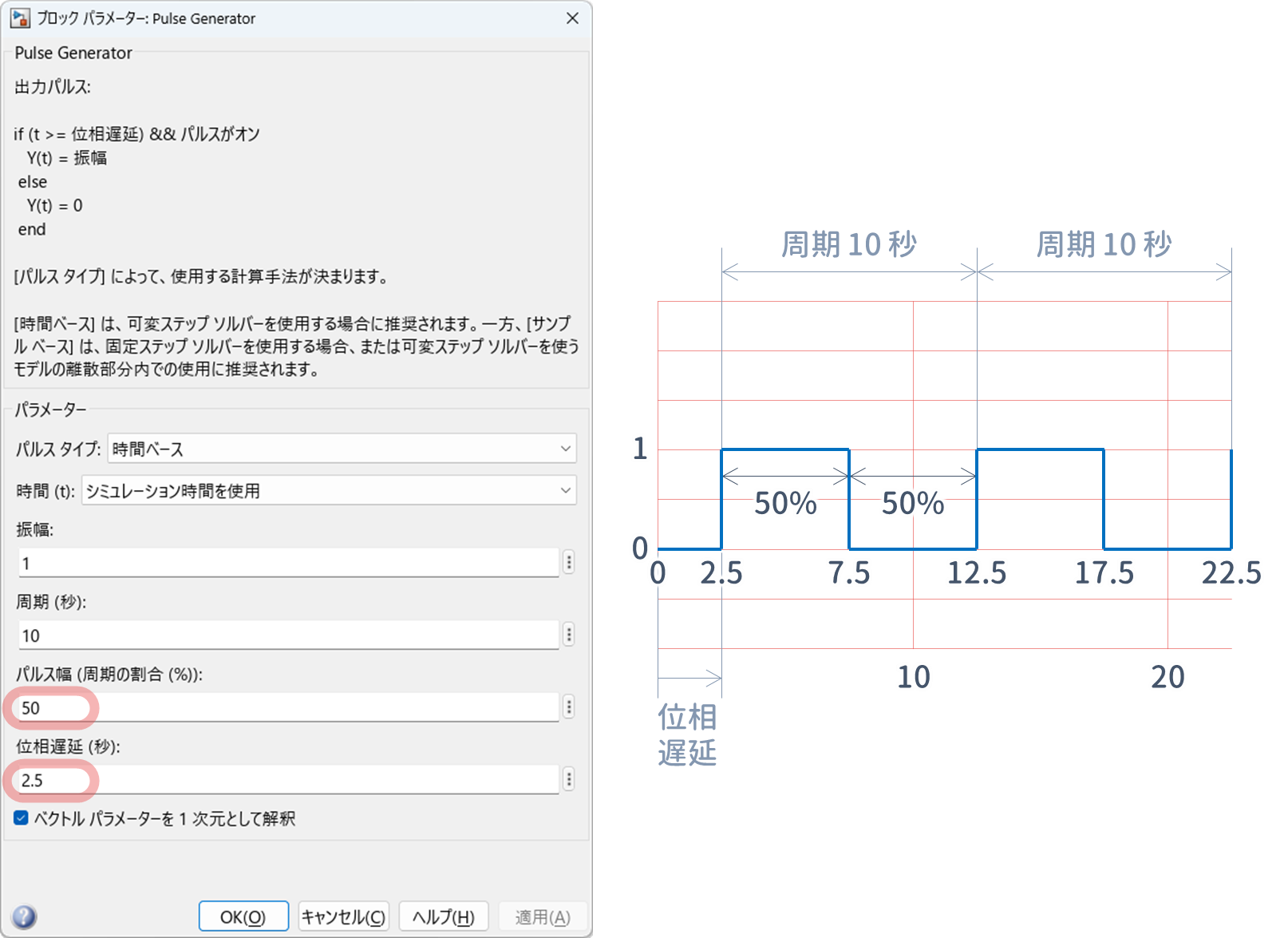
3.2.2 Pulse Generator の設定
入力信号を,10 秒ごとにステップ状に 0 と 1 の 2 値に変化させます.この 2 値の比は 50% です.また,2.5 秒ずらすことで,ステップ状に変化する "$\tt Scope$" での時間を 10 秒間のうちで 2.5 秒と 7.5 秒にします.
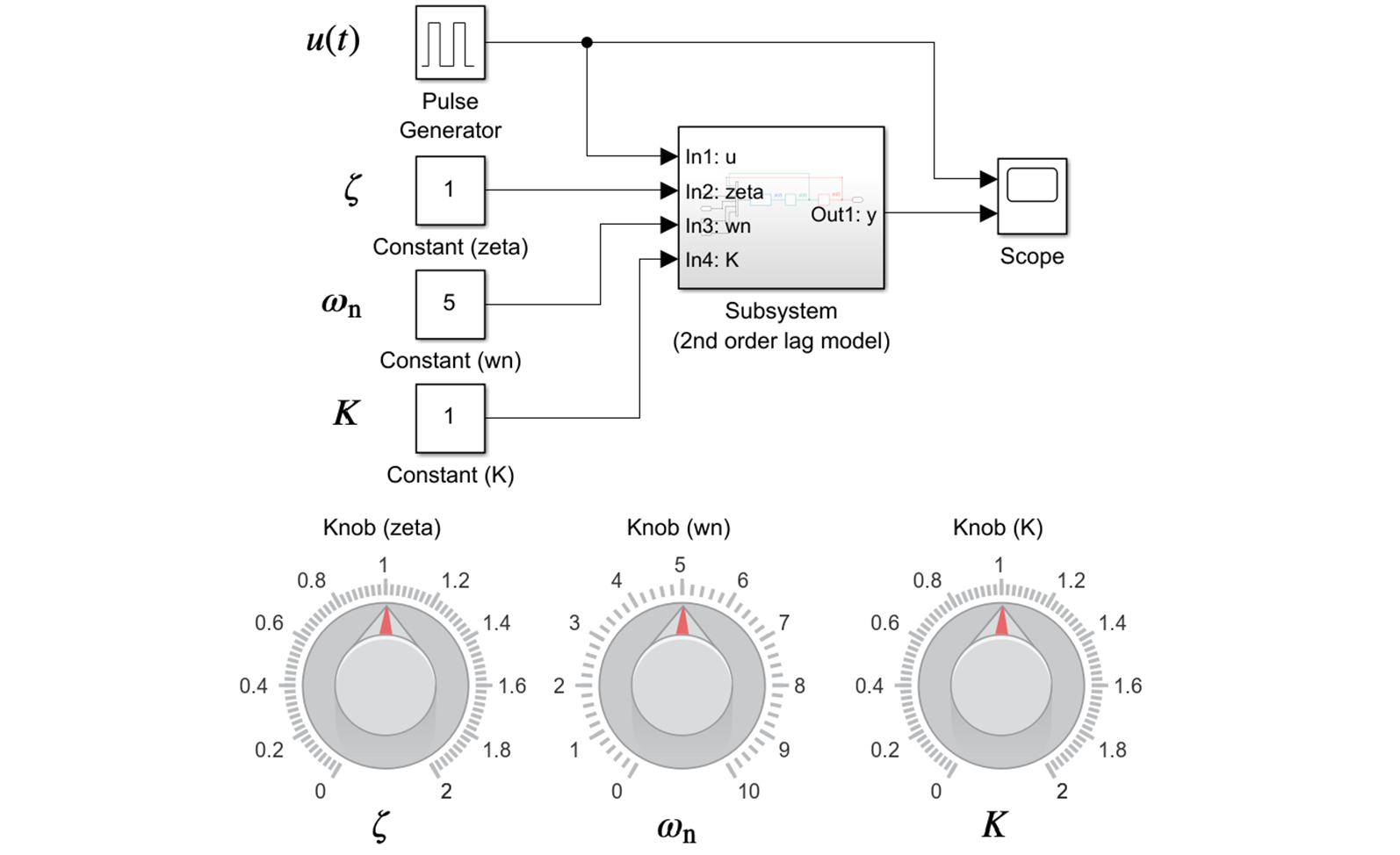
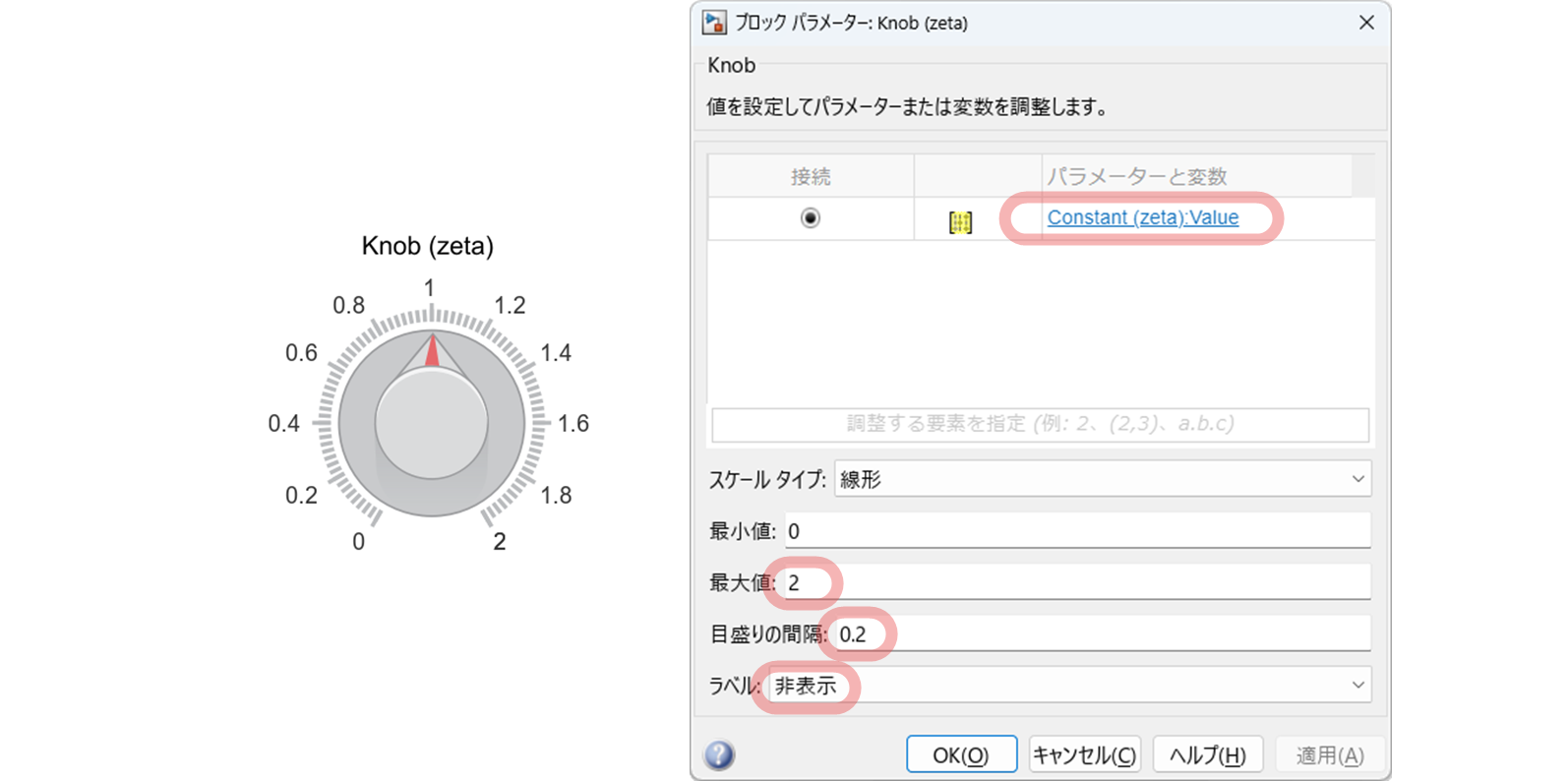
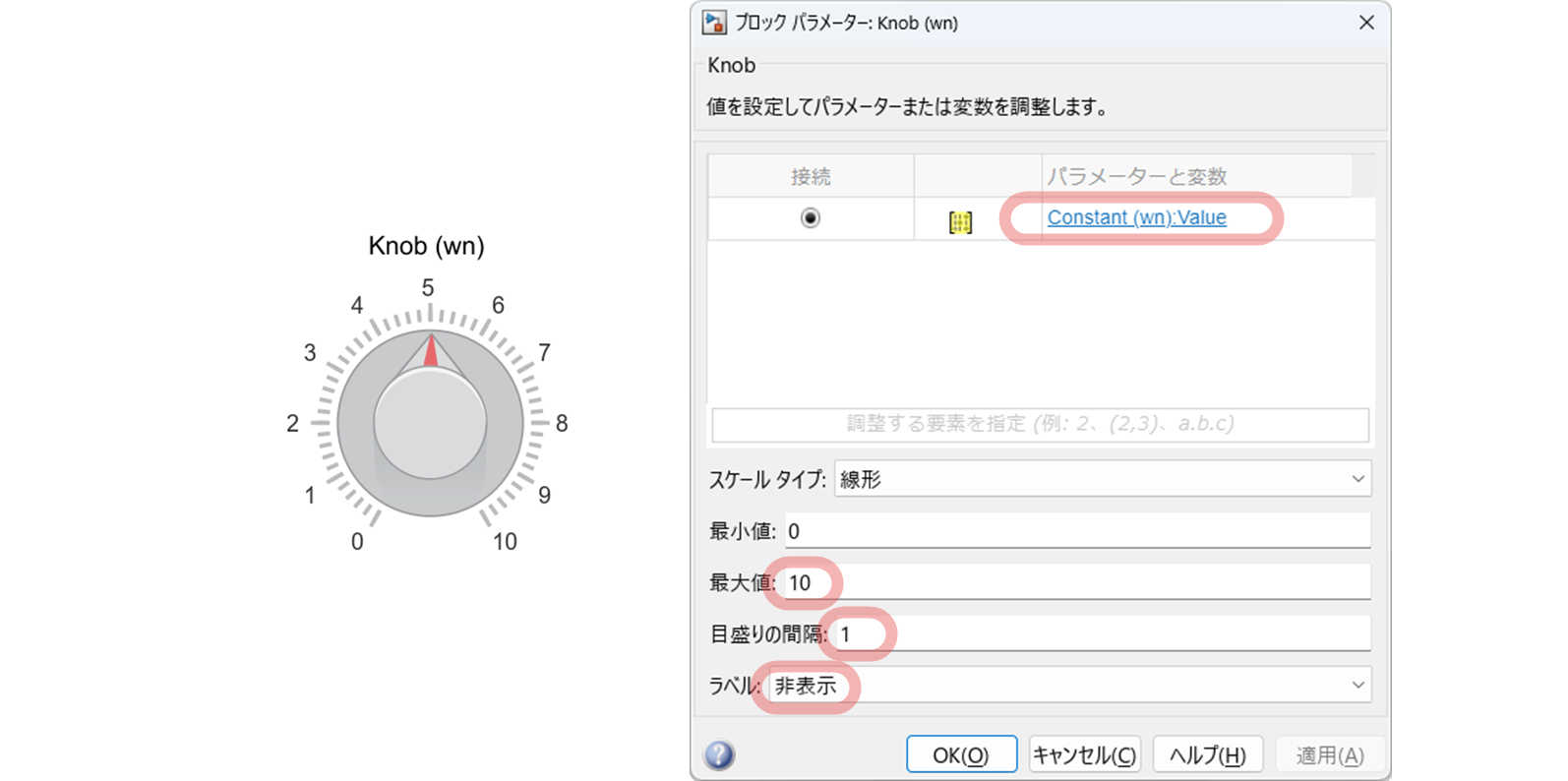
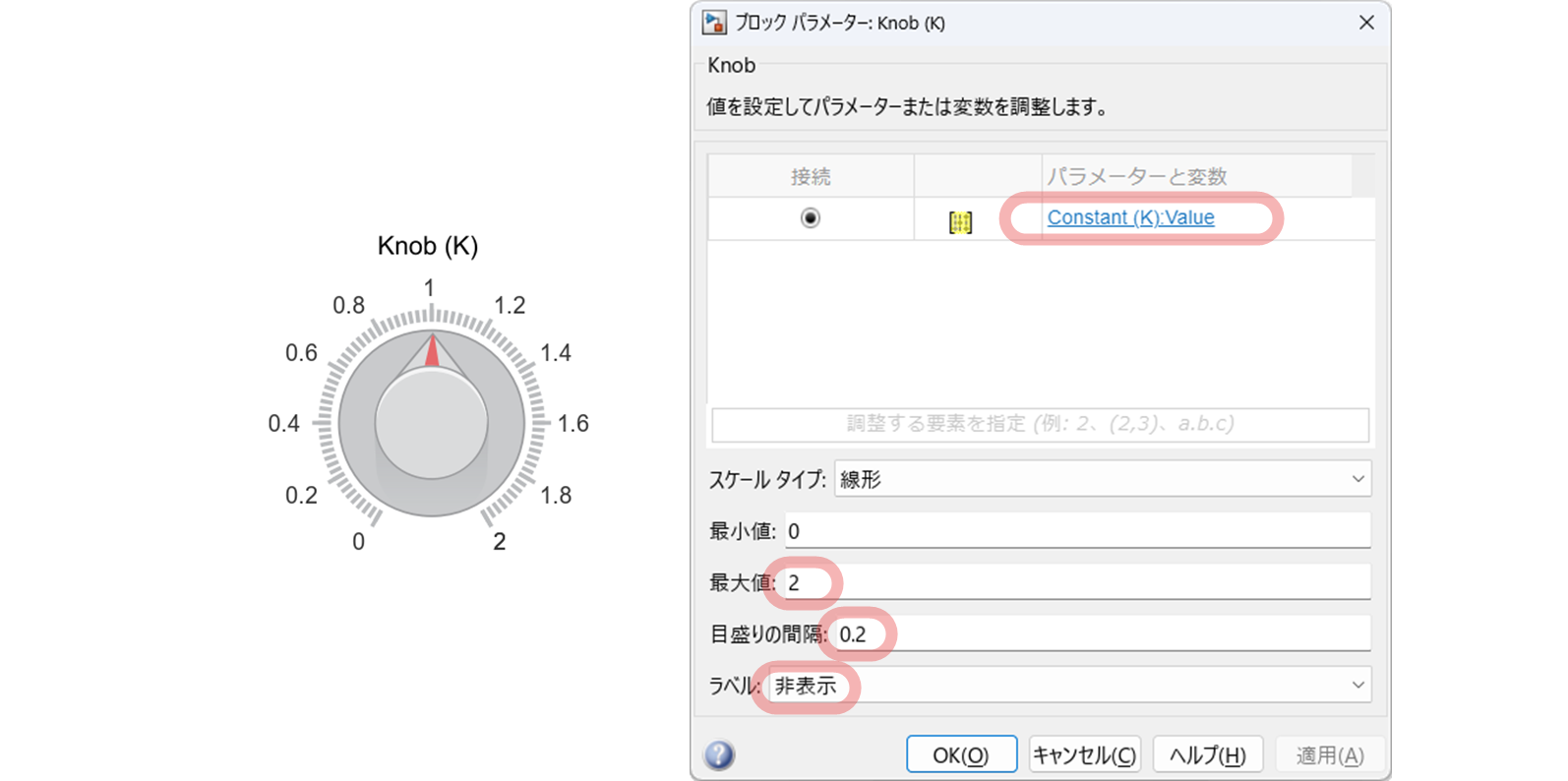
3.2.3 Knob の設定
"$\tt Knob$" はダイヤルでパラメータの値を調整するための Simulink ブロックです.今回は,シミュレーションを行っている最中に,"$\tt Knob$" のダイヤルををマウスで回転させることで $\zeta$, ${\omega}_{\rm n}$, $K$ の値を変化できるようにします.
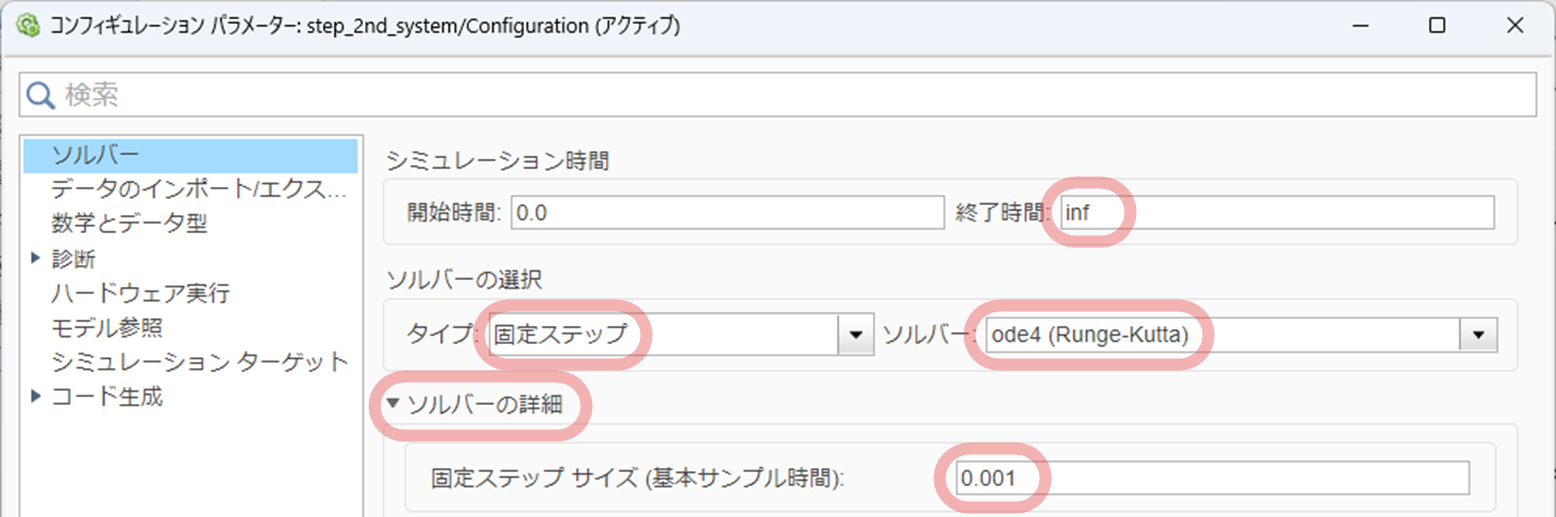
3.3 モデルコンフィギュレーションパラメータの設定
サンプリング周期を 0.001 [s] として $(3)$ 式で示した微分方程式を 4 次のルンゲ=クッタ法で数値的に解くため,以下のように設定します.
3.4 シミュレーションページングの設定
Simulink でシミュレーションをすると高速でグラフが描画がされてしまい,変化がわかりにくいです.そこで,シミュレーションページングを設定します.
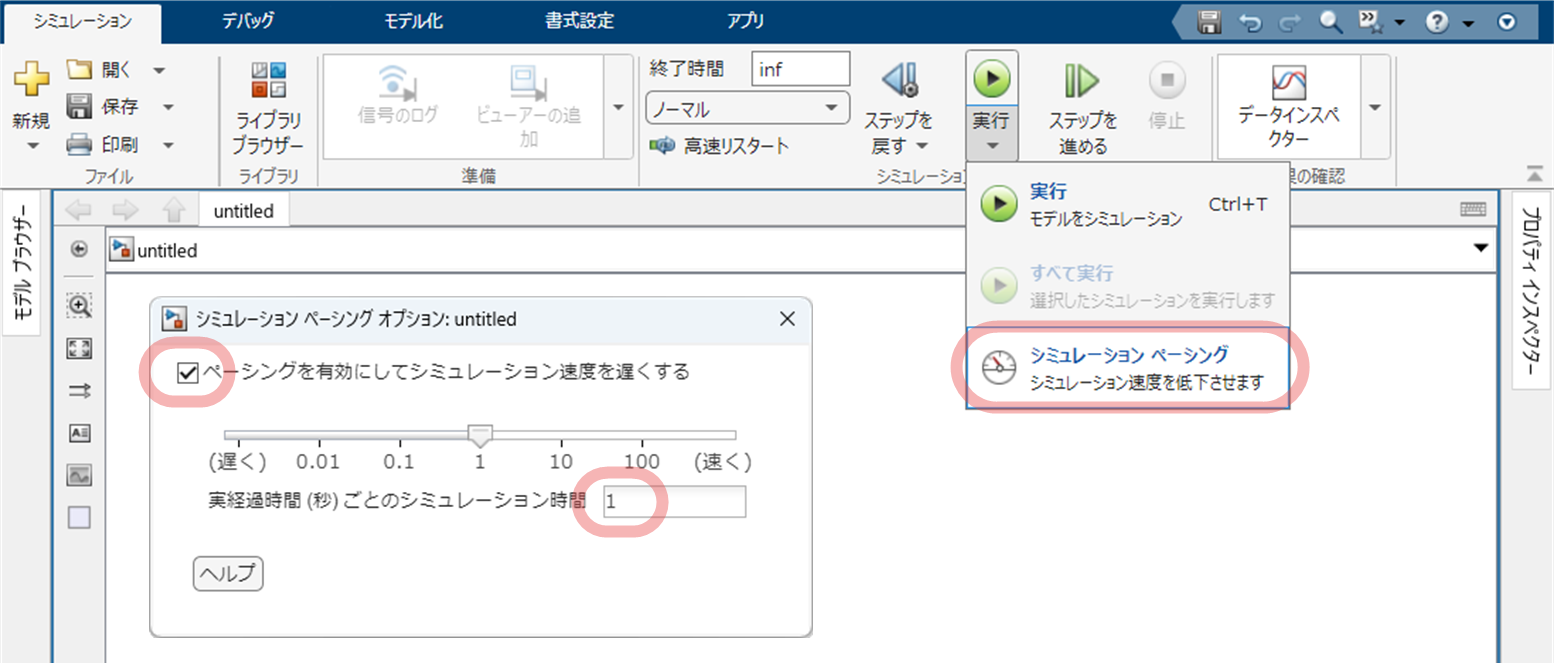
作成した Simulink モデルの「シミュレーション / 実行」で「シミュレーションページング」を選択すると,下図のウィンドウが開きますので,
- 「ページングを有効にしてシミュレーション速度を遅くする」をチェック
としてください.
このとき,標準では,
- 「実経過時間(秒)ごとのシミュレーション時間」が「1」
となっているので,1 秒間のシミュレーションが 1 秒で実行されます(1 倍速).
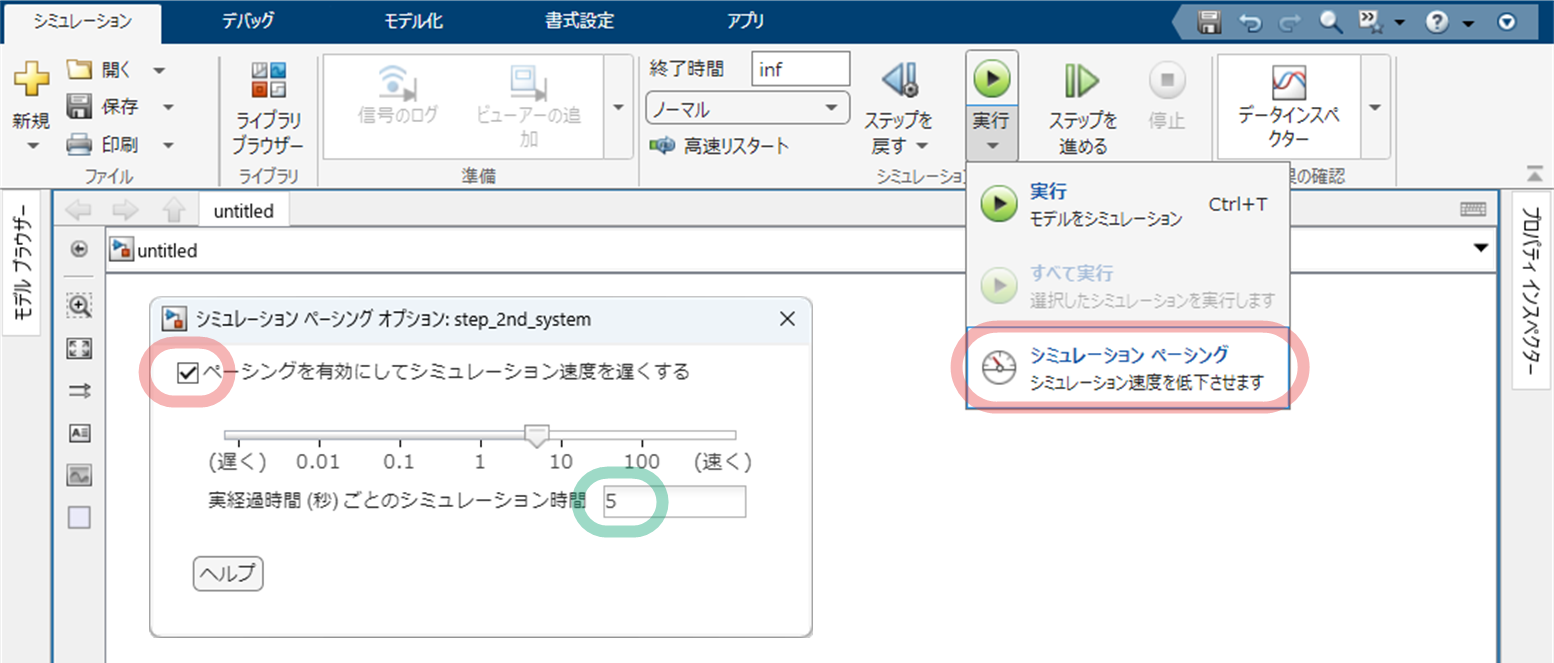
今回は,
- 「実経過時間(秒)ごとのシミュレーション時間」を「5」
に変更することで,5 秒間のシミュレーションが 1 秒で実行されるようにします(5 倍速).
4. 実行例
実行した様子の動画を YouTube にアップしていますので,確認してみてください.先に述べたように,実行速度は 5 倍速としています.マウスでダイヤルを回すと,2 次遅れ系の 3 つのパラメータ $\zeta$, ${\omega}_{\rm n}$, $K$ の役割が感じ取れるのではないでしょうか.
5. おわりに
ということで,もっと良い方法があるかもしれませんが,ダイヤルでパラメータ ${\omega}_{\rm n}$, $\zeta$, $K$ の値を変化させながら,シミュレーションで結果を確認できる Simulink モデルを作成してみました.
ちなみに,ここで紹介したした Simulink モデルは,PID 制御の目標値フィルタ($K = 1$ とした 2 次遅れ要素)のパラメータを実験しながら調整するために作成したものです.