Simulink を利用した非線形シミュレーション ー "Fcn", "User-defined Function", "MATLAB Function" の活用法！

0. 配布ファイル

　本記事で利用した MATLAB 関連ファイルは

• https://github.com/Prof-Carter/nonlinear_simulation

に公開していますので，ご自由にどうぞ！ R2018a 以降で利用できると思います．

なお，配布するファイル等の動作保証およびテクニカルサポート，発生した損害に対する責任は負いません．

1. はじめに

　はじめに言っておきますが，特に目新しいことは記述していません！ 忘備録のような感じですので，悪しからず．

　さて，制御屋さんは，通常，実験装置を動かす前に（実験装置を動かして壊してしまう前に），シミュレーションにより動作確認をします．たとえば，PI-D コントローラ（微分先行型 PID コントローラ）

\begin{align}
    u(t) = &\;{k}_{\rm P}e(t) 
         + {k}_{\rm I}\int_{0}^{t}e(t){\rm d}t 
         - {k}_{\rm D}\dot{y}(t),\quad
    e(t) = r(t) - y(t)
    \tag{1}
\end{align}

を利用して，鉛直面を回転するアーム系の角度制御を行うことを考えてみましょう．

鉛直面を回転するアーム系

　このアーム系の運動方程式は

\begin{align}
    J\ddot{y}(t) = u(t) - Mgl\sin{y}(t) - c\,\dot{y}(t)
    \tag{2}
\end{align}

となり，非線形微分方程式となります．ただし，$J$：アームの軸まわりの慣性モーメント，$M$：アームの質量，$l$：アームの軸から重心までの長さ，$c$：粘性摩擦係数，$g$：重力加速度です．

　モデルベースでコントローラを設計する際には，アームが $y(t) = 0$ 近傍で動作するとして，$(2)$ 式を

\begin{align}
    &
    J\ddot{y}(t) = u(t) - Mgl\,y(t) - c\,\dot{y}(t)
    \\
    &\Longrightarrow\quad
    y(s) = P(s)u(s),\ 
    P(s) = \dfrac{1}{J{s}^{2} + cs + Mgl}
    \tag{3}
\end{align}

のように線形化することが多いですが，制御性能を検証するシミュレーションは，実験装置の動作に近い状況で行う方が良いでしょう．そのために，制御対象のモデルを線形化した $(3)$ 式ではなく，非線形項を含む $(2)$ 式としてシミュレーションを行います．

　MATLAB 関数 "ode45" を利用してゴリゴリとプログラミングして非線形微分方程式 $(2)$ 式を解き，シミュレーションを行う人もいると思います．でも，ブロック線図で記述してシミュレーションした方がわかりやすいですよね．そこで，本記事では，視覚的にわかりやすい Simulink を利用して非線形微分方程式 $(2)$ 式を記述し，シミュレーションを行う方法について説明します．個人的には，Simulink が使えることが MATLAB の最大のメリットだと考えています．

　ちなみに，私が初めて MATLAB/Simulink を利用したのは 1992 年のときでして，修士課程 1 年の学生でした．当時はもっぱら MS-DOS 上で C 言語によりルンゲ・クッタ (Runge–Kutta) 法のプログラムを記述してシミュレーションを行い，グラフを描画していましたので，Simulink の登場はなかなか衝撃的でした．Simulink を使えば，Macintosh (Mac) 上でブロック線図を並べるだけでシミュレーションが行えて，グラフの描画も驚くほど簡単なんです！　なお，当時は Simulink ではなく Simulab という名前でした（このことを覚えている人は MATLAB 黎明期を過ごした方でしょう）．Wikipedia によると，私が最初に利用したのは Ver.4 だったようです．1994 年には Macintosh の OS (System 7) だけでなく Windows 3.1 にも対応した伝説の Ver.4.2c が販売され，広く普及したように思います．当時の Macintosh はユーザインタフェースは素晴らしかったのですが，なにせ実行速度が遅いうえに，恐怖の爆弾マークが出現する品物でしたので…　

　脱線してしまいました．話を元に戻しましょう．

　さて，非線形微分方程式 $(2)$ 式を Simulink で記述する方法として，たとえば，以下のようなものがあります．

• 方法 0："Sin", "Gain", "Sum" などといった基本的な数学関数の Simulink ブロックを組み合わせる
• 方法 1："Fcn" を利用する　$\cdots\cdots$ MATLAB R2020b で廃止されましたが，まだ利用することができます！
• 方法 2："User-defined Functions" を利用する
• 方法 3："MATLAB Function" を利用する

これらの方法を順に説明しましょう．

2. 基本的な数学関数の Simulink ブロックを組み合わせてみよう！

　この方法では，基本的な数学関数の Simulink ブロックを組み合わせて，アーム系の非線形微分方程式 $(2)$ 式を表現します．このとき，アーム系の PI-D 制御の非線形シミュレーションを行うための Simulink モデルは以下のようになります．

基本的な数学関数の Simulink ブロック "arm_nonlinear_sim_pi_d_cont_basic.slx"

　アーム系の場合，非線形微分方程式は $(2)$ 式のように，比較的単純なので，このように簡単に表現できますが，複雑な非線形項を持つ場合，ブロックの組み合わせや結線が煩わしくなるという欠点があります．

3. ひとつの Simulink ブロックにより非線形微分方程式を記述してみよう！

　上記の欠点に対処するために，$(2)$ 式を

\begin{align}
    \ddot{y}(t) = \dfrac{u(t) - Mgl\sin{y}(t) - c\,\dot{y}(t)}{J}
    \tag{4}
\end{align}

と書き換え，$(4)$ 式の右辺をひとつの Simulink ブロックで記述します．このことを実現可能な Simulink ブロックとしては

• Simulink ブロック "Fcn"
• Simulink ブロック "Interpreted MATLAB Function"
• Simulink ブロック "MATLAB Function"

があります．アーム系の場合，これらの Simulink ブロックには 3 つの信号

• u(1)：$y(t)$
• u(2)：$\dot{y}(t)$
• u(3)：$u(t)$

が入力され，$(4)$ 式の右辺を

(u(1) - M*g*l*sin(u(2)) - c*u(3))/J

のように記述します．そして，Simulink ブロックの出力は $(4)$ 式の左辺 $\ddot{y}(t)$ となります．

　ここで説明する Simulink ブロックの特徴を以下に示します．

Simulink ブロック	実行速度	記述の容易さ	コード生成	拡張性
"Fcn"	速い	容易	対応
"Interpreted MATLAB Function"	遅い	容易	非対応
"MATLAB Function"	そこそこ速い	複雑	対応

4. Simulink ブロック "Fcn" を使ってみる！

4.1　Simulink ブロック "Fcn" って R2020b 以降でも使えるの？

(2023/07/01 追記）

R2023a では Simulink ブロック "Fcn" が復活していました！

　MATLAB R2020b 以降では，下図に示すとおり，非線形項を式で記述するための Simulink ブロック "Fcn" が Simulink ブロックライブラリ "User-defined Functions" から削除されています．理由は不明ですが… 便利だったのに…

　R2020b 以降のバージョンでは，表向き，Simulink ブロック "Fcn" はないように見えます（マスワークスさんが隠してしまいました…）．

　たとえば，R2020a では，

>> doc fcn

と入力すると，Simulink ブロック "Fcn" のドキュメンテーションが

R2020a での "Fcn" のドキュメンテーション

のように出力されます．一方，R2020b では，

>> doc fcn

と入力すると，

R2020b での "Fcn" の検索結果

となり，Simulink ブロック "Fcn" のドキュメンテーションは表示されません．

　でも，安心してください．実は R2020b 以降でも（少なくとも本記事を執筆している時点での最新バージョン R2022b でも）Simulink ブロック "Fcn" を利用することができます！ そのために，

>> simulink3

と入力してください．そうすると，Simulink Block Library 5.0 のウィンドウが立ち上がります．

Simulink Block Library 5.0

そして，ライブラリ "Functions & Tables" を開くと，Simulink ブロック "Fcn" が見つかります！

Simulink ライブラリ "Functions & Tables"

　ちなみに，R2020b での Simulink ブロック "Fcn" のドキュメンテーションは，ライブラリ "Functions & Tables" にある "Fcn" をダブルクリックした後，ヘルプをクリックすることで表示することができます．

R2020b 以降での "Fcn" のドキュメンテーション

R2020b 以降では，このように，

Fcn は推奨されません。さらに複雑な式には MATLAB Function ブロックを使用します。それほど複雑でない式には、同じ動作をモデル化するブロックでの置き換えを検討してください。

という表示がされるようになりましたが，無視して使っちゃいましょう！

4.2　Simulink ブロック "Fcn" の使い方は超簡単！

　Simulink ブロック "Fcn" を利用すると，アーム系の PI-D 制御の非線形シミュレーションを行うための Simulink モデルは以下のようになります．

PI-D 制御の非線形シミュレーションを行うための Simulink モデル "arm_nonlinear_sim_pi_d_cont.slx"

　また，線形化された伝達関数表現 $(3)$ 式に基づいて，PI-D 制御の線形シミュレーションを行うための Simulink モデルは，以下のようになります．

PI-D 制御の線形シミュレーションを行うための Simulink モデル "arm_linear_sim_pi_d_cont.slx"

　線形シミュレーションと非線形シミュレーションを比較するための M ファイルを以下に示します．なお，PI-D コントローラのゲインの設計については，付録で説明しています．

M ファイル "arm_pi_d_simulation.m"

close all
clear
format compact

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' 制御対象 P(s)')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

l = 2.04e-01;
M = 3.90e-01;
J = 7.12e-02;
c = 6.95e-01;
g = 9.81e+00;

% --------------------
a0 = M*g*l/J;
a1 = c/J;
b0 = 1/J;

% --------------------
s = tf('s');

sysP = b0/(s^2 + a1*s + a0)

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' 規範モデル M2(s)')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

wm     = 6;
alpha1 = 1.4;

sysM2 = wm^2/(s^2 + alpha1*wm*s + wm^2)

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' コントローラのゲイン')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

kI = (a0*wm)/(alpha1*b0)
kP = wm^2/b0
kD = (alpha1^2*wm^2 - a1*alpha1*wm + a0)/(alpha1*b0*wm)

sysC1 = kP + kI/s + kD*s;
sysC2 = kP + kI/s;

disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp(' 目標値 r(s) から制御出力 y(s) への伝達関数 Gyr(s)')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++++')

sysGyr = minreal(sysP*sysC2/(1 + sysP*sysC1))

num = 0;
for rc_deg = [30 60 120 240]   % 目標値 (deg)
    num = num + 1;

    % --------------------    
    rc = deg2rad(rc_deg);  % 目標値 (rad)
    dc = 0;                % 外乱
    
    sim('arm_linear_sim_pi_d_cont')     % 線形シミュレーション
    y_linear = y;
    
    sim('arm_nonlinear_sim_pi_d_cont')  % 非線形シミュレーション
    
    % --------------------
    figure(num)
    subplot('Position',[0.15 0.15 0.775 0.775])
    
    plot(t,rad2deg(y_linear),'LineWidth',1.5)
    hold on
    plot(t,rad2deg(y),'LineWidth',1.5)
    hold off
    
    set(gca,'FontName','Arial','FontSize',14)
    
    xlabel('$t$ [s]','Interpreter','latex','FontSize',16)
    ylabel('$y(t)$ [deg]','Interpreter','latex','FontSize',16)
    
    legend({'Linear Simulation',...
            'Nonlinear Simulation'},...,
            'Interpreter','latex','FontSize',16,...
            'Location','SouthEast')
    
    ylim([0 rc_deg*6/4])
    set(gca,'YTick',0:rc_deg/4:rc_deg*6/4)
    
    grid on
end

figure(1); movegui('northwest')
figure(2); movegui('northeast')
figure(3); movegui('southwest')
figure(4); movegui('southeast')

M ファイル "arm_pi_d_simulation.m" の実行結果を以下に示します．

M ファイル "arm_pi_d_simulation.m" の実行結果

>> arm_pi_d_simulation
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 制御対象 P(s)
+++++++++++++++++++++++++++++++++++++++++++++++++++++++

sysP =
 
          14.04
  ---------------------
  s^2 + 9.761 s + 10.96
 
連続時間の伝達関数です。

+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 規範モデル M(s)
+++++++++++++++++++++++++++++++++++++++++++++++++++++++

sysM =
 
         36
  ----------------
  s^2 + 8.4 s + 36
 
連続時間の伝達関数です。

+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 コントローラのゲイン
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
kI =
    3.3449
kP =
    2.5632
kD =
   -0.0040
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 目標値 r(s) から制御出力 y(s) への伝達関数 Gyr(s)
+++++++++++++++++++++++++++++++++++++++++++++++++++++++

sysGyr =
 
         36
  ----------------
  s^2 + 8.4 s + 36
 
連続時間の伝達関数です。

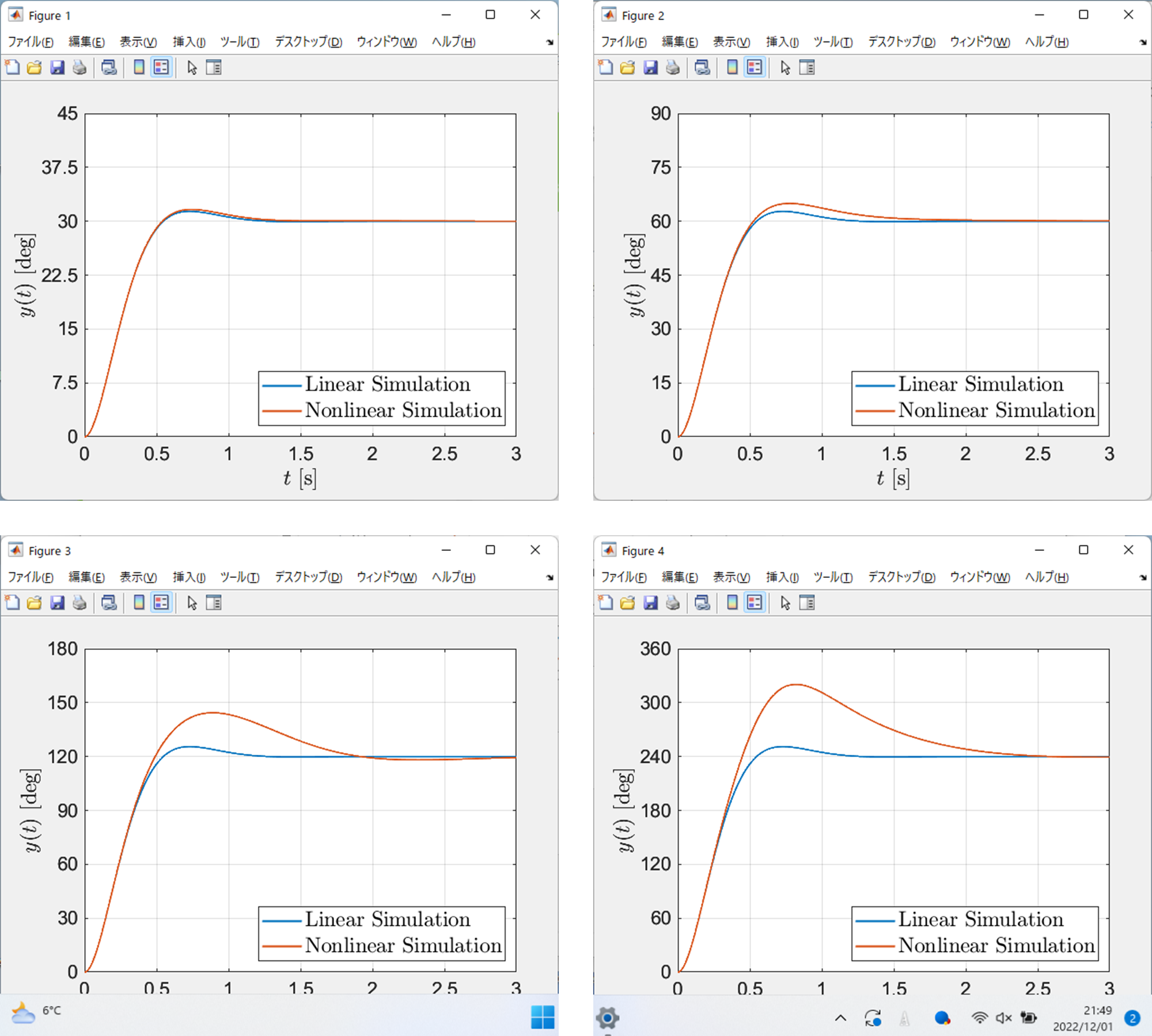
このように，目標角度が大きくなると，線形化誤差の影響が大きくなることが確認できます．

5. Simulink ブロック "Interpreted MATLAB Function" を使ってみる！

　非線形シミュレーションを行うだけであれば，Simulink ブロック "Fcn" の代わりに Simulink ブロック "Interpreted MATLAB Function" を利用することも可能です．

Simulink ブロック "Interpreted MATLAB Function"

　"Interpreted MATLAB Function" の使用方法は "Fcn" と同じですので，"Fcn" に使い慣れた人にはオススメかもしれません．PI-D 制御の非線形シミュレーションを行うための Simulink モデルを以下に示します．

PI-D 制御の非線形シミュレーションを行うための Simulink モデル "arm_nonlinear_sim_pi_d_cont_Interpreted_MATLAB_Function.slx"

　"Interpreted MATLAB Function" を使用する場合，以下の問題があることに注意する必要があります．

• "Interpreted MATLAB Function" のシミュレーションの実行速度は "Fcn" より遅くなります．アーム系の PI-D 制御の非線形シミュレーションの場合，おおよそ 3 倍程度の時間がかかります．
• "Interpreted MATLAB Function" は，実機実験を行う（Simulink モデルからコード生成を行う）ことに対応していません．

　M ファイル "arm_pi_d_simulation_Interpreted_MATLAB_Function.m" を実行すると，非線形シミュレーションの結果が表示されます．

6. Simulink ブロック "MATLAB Function" を使ってみる！

　実機実験を行う（Simulink モデルからコード生成を行う）ことに対応した Simulink ブロックとして，"MATLAB Function" があります．その使い方は少々，癖がありますが，慣れれば問題ない…

6.1　"MATLAB Function" の使い方をマスターしよう！

　"MATLAB Function" の使い方については，遠藤さんの解説に詳しく書かれています．

Simulink ブロック "MATLAB Function"

．PI-D 制御の非線形シミュレーションを行うための Simulink モデルを以下に示します．

PI-D 制御の非線形シミュレーションを行うための Simulink モデル "arm_nonlinear_sim_pi_d_cont_MATLAB_Function.slx"

　"MATLAB Function" の設定について説明します．"MATLAB Function" をダブルクリックすると，関数を記述するウィンドウに切り替わりますので，

"MATLAB Function" による関数作成

function ddy = fcn(u,M,g,l,c,J)

ddy = (u(3) - M*g*l*sin(u(1)) - c*u(2))/J;

と入力してください．このように，関数の入力引数には，3 次元の入力信号 u (すなわち，$[y(t) \ \ \dot{y}(t) \ \ u(t)]$) だけでなく，関数内で使用されているパラメータ M, g, l, c, J (すなわち，$M$, $g$, $l$, $c$, $J$） も含まれていることに注意してください．

　つぎに，入力引数が入力信号なのか，パラメータなのかを設定します．そのために，関数を記述するウィンドウで「データの編集」を選択してください．なお，MATLAB のバージョンによって「データの編集」の場所が違うので，注意してください（このあたりのユーザインタフェースは継承してほしいものです）．そして，以下に示すように，Scope（スコープ）のプロパティを設定します．

"MATLAB Function" のプロパティの設定 (R2022b)
入力信号の設定
出力信号の設定
パラメータの設定

【注意】
MATLAB のバージョンによっては（確認した R2018a および R2020a～R2022b のなかでは，R2021a, R2020b, R2020a が相当），

のような警告が出ますが，ちゃんと動作はします（警告が出る理由は私にはわかりませんでした… 要素はちゃんと 3 つあるのに…）．マスワークス社のサポート様に質問したところ，

利用のバージョンにより、MATLAB Function 内で入力信号 u のサイズが的確に内部で定義できないために生じている問題です．入力 u のサイズを継承の -1 から 3 に変更すると，エラーなく実行できます．

とのことでした．要は，u がベクトルであるとき，そのサイズを正しく認識できていないということです．たとえば，R2020a の場合，"MATLAB Function" をダブルクリックした後，以下のように変更し，手動で u のサイズを指定します．

そして，M ファイル "arm_pi_d_simulation_MATLAB_Function.m" を実行すると，非線形シミュレーションの結果が表示されます．

6.2　Simulink ブロック "MATLAB Function" を使う利点

　このように，"MATLAB Function" を利用する場合は，他の方法に比べて操作が面倒です．しかし，様々な MATLAB 関数の利用がサポートされているので，いろいろと高機能なことができます．

6.2.1　アニメーション表示

　以下の Simulink モデル "arm_nonlinear_sim_pi_d_cont_MATLAB_Function_animation.slx" を利用すると，アニメーションを表示させることができます．

PI-D 制御のアニメーション表示をするための Simulink モデル "arm_nonlinear_sim_pi_d_cont_MATLAB_Function_animation.slx"

MATLAB Function（アニメーション表示）

function fcn(t,y,r)

if mod(t*1000,25) == 0
    L = 0.4;

    figure(10); clf;
    axis off
    set(gcf,'Color','w')

    plot([-0.55 -0.55 0.55 0.55 -0.55],[-0.55 0.55 0.55 -0.55 -0.55],'Color',[1 1 1],'LineWidth',2)
    hold on
    axis('square')
    axis([-0.55 0.55 -0.55 0.55]);
    set(gca,'FontSize',12,'FontName','Arial')
    set(gca,'XTick',[])        % 横軸の目盛
	set(gca,'XTickLabel',[])   % 横軸の目盛のラベル
	set(gca,'YTick',[])        % 縦軸の目盛
	set(gca,'YTickLabel',[])   % 縦軸の目盛のラベル
    
    % アーム取り付け台
    plot([-0.05 0.05],[0 0],'Color',[0.8 0.8 0.8],'LineWidth',25)
    
    % 足
    plot([-0.125 -0.125],[-0.1 -0.015],'k','LineWidth',4)
    plot([ 0.125  0.125],[-0.1 -0.015],'k','LineWidth',4)

    plot([-0.15 -0.1],[-0.095 -0.095],'k','LineWidth',4)
    plot([ 0.15  0.1],[-0.095 -0.095],'k','LineWidth',4)

    % 台
    plot([-0.175 0.175],[-0.06 -0.06],'Color',[0.6 0.6 0.6],'LineWidth',5)

    % 地面
    plot([-0.55 0.55],[-0.325 -0.325],'Color',[205 161 111]/255,'LineWidth',105)

    % アーム
    plot([0 -L*sin(y)],[0 -L*cos(y)],'Color',[0 112 192]/255,'LineWidth',12.5);

    % 初期値，目標値
    plot([0 0],[0 -2*L],'--','Color',[232 71 70]/255)
    plot([0 -2*L*sin(r)],[0 -2*L*cos(r)],'--','Color',[232 71 70]/255)
    
    % 時間表示
    text(0.5,0.5,sprintf('%2.1f [s]',t),'FontSize',12,'FontName','Arial')
    
    % 目標値表示
    text(0.5,0.55,sprintf('r = %4.0f [deg]',r*180/pi),'FontSize',12,'FontName','Arial')
       
    hold off
end

Simulink モデルを実行する前に，

M ファイル "***.m" の実行

>> arm_pi_d_simulation_MATLAB_Function

＜略＞

+++++++++++++++++++++++++++++++++++++++++++++++++++++++
 コントローラのゲイン
+++++++++++++++++++++++++++++++++++++++++++++++++++++++
kI =
    3.3449
kP =
    2.5632
kD =
   -0.0040
＜略＞

>> close(1:3)
>> rc_deg = 240;
>> rc = deg2rad(rc_deg);
>> dc = 0;

と入力してから，Simulink モデル "arm_nonlinear_sim_pi_d_cont_MATLAB_Function_animation.slx" を実行してください．そうすると，以下のようにアニメーションが表示されます．

6.2.2　Symbolic Math Toolbox との連携

　MATLAB/Simulink Advent Calendar 2022 の 9 日目の WandererEng さんの記事

では，Symbolic Math Toolbox を利用して非線形微分方程式を導出し，それを "MATLAB Function" で自動的に記述する方法が紹介されています！

　この結果をアーム系に適用してみます．ここで，

• th：アーム角度 $y(t) = \theta(t)$
• dth：アーム角速度 $\dot{y}(t) = \dot{\theta}(t)$
• ddth：アーム角加速度 $\ddot{y}(t) = \ddot{\theta}(t)$
• tau：入力トルク $u(t) = \tau(t)$

です．配布する M ファイル

M ファイル "building_MATLAB_Function.m"

clear
format compact

syms M g l J Jg c real
syms th dth ddth tau real

q   = th;       % 角度　　　：q = θ
dq  = dth;      % 角速度　　：ω = dθ/dt
ddq = ddth;     % 角加速度　：dω/dt
u   = tau;      % 入力トルク：τ

% ------------------------------------------------------
disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 重心座標 (px, py)')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

px = - l*sin(q)
py = - l*cos(q)

disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ d(px)/dt')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

dpx = diff(px,q)*dq

disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ d(py)/dt')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

dpy = diff(py,q)*dq

% ------------------------------------------------------
disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 運動エネルギー K')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

K = (1/2)*M*dpx^2 + (1/2)*M*dpy^2 + (1/2)*Jg*dq^2

disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 位置エネルギー U')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

U = M*g*py

disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 損失エネルギー D')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

D = (1/2)*c*dq^2

disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ ラグランジアン L = K- U')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

L = K - U

% ------------------------------------------------------
disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ L を dq/dt で偏微分')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

dLq  = diff(L,dq)

disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ L を dq/dt で偏微分したものを時間微分')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

ddLq = diff(dLq,dq)*ddq + diff(dLq,q)*dq

disp(' ')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ ラグランジュの運動方程式')
disp('++++++++++++++++++++++++++++++++++++++++++++++++++')

eq = ddLq - diff(L,q) + diff(D,dq) - u;
eq = subs(eq,Jg,J-M*l^2);
eq = simplify(eq');

ddtheta = solve(eq,ddth)

% ---------------------------------------------------------------
new_system('sim_hoge') 
open_system('sim_hoge')

matlabFunctionBlock('sim_hoge/arm_model',...
    ddtheta,...
    'vars',[th dth u J c M g l],...
    'outputs',{'ddth'})

を実行してください．その結果，

M ファイル "building_MATLAB_Function.m" の実行結果

>> building_MATLAB_Function

++++++++++++++++++++++++++++++++++++++++++++++++++
+ 重心座標 (px, py)
++++++++++++++++++++++++++++++++++++++++++++++++++
px =
-l*sin(th)
py =
-l*cos(th)
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ d(px)/dt
++++++++++++++++++++++++++++++++++++++++++++++++++
dpx =
-dth*l*cos(th)
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ d(py)/dt
++++++++++++++++++++++++++++++++++++++++++++++++++
dpy =
dth*l*sin(th)
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ 運動エネルギー K
++++++++++++++++++++++++++++++++++++++++++++++++++
K =
(Jg*dth^2)/2 + (M*dth^2*l^2*cos(th)^2)/2 + (M*dth^2*l^2*sin(th)^2)/2
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ 位置エネルギー U
++++++++++++++++++++++++++++++++++++++++++++++++++
U =
-M*g*l*cos(th)
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ 損失エネルギー D
++++++++++++++++++++++++++++++++++++++++++++++++++
D =
(c*dth^2)/2
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ ラグランジアン L = K- U
++++++++++++++++++++++++++++++++++++++++++++++++++
L =
(Jg*dth^2)/2 + M*g*l*cos(th) + (M*dth^2*l^2*cos(th)^2)/2 + (M*dth^2*l^2*sin(th)^2)/2
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ L を dq/dt で偏微分
++++++++++++++++++++++++++++++++++++++++++++++++++
dLq =
M*dth*l^2*cos(th)^2 + M*dth*l^2*sin(th)^2 + Jg*dth
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ L を dq/dt で偏微分したものを時間微分
++++++++++++++++++++++++++++++++++++++++++++++++++
ddLq =
ddth*(M*l^2*cos(th)^2 + M*l^2*sin(th)^2 + Jg)
 
++++++++++++++++++++++++++++++++++++++++++++++++++
+ ラグランジュの運動方程式
++++++++++++++++++++++++++++++++++++++++++++++++++
ddtheta =
-(c*dth - tau + M*g*l*sin(th))/J

と表示された後，Simulink モデル "sim_hoge.slx" のなかに "MATLAB Function" である "arm_model" が自動生成されます．

自動生成された "MATLAB Function"

これを利用して，Simulink モデルを作成すると，以下のようになります．

PI-D 制御の非線形シミュレーションを行うための Simulink モデル "arm_nonlinear_sim_pi_d_cont_Interpreted_MATLAB_Function_auto.slx"

【注意】
自動生成された "MATLAB Function" ("arm_model") では，8 つ入力引数が設定されています．最初の 3 つは，$y(t) = \theta(t)$ (th), $\dot{y}(t) = \dot{\theta}(t)$ (dth), $u(t) = \tau(t)$ (tau) ですので，問題ありません．一方，残りの 5 つ $J$ (J), $c$ (c), $M$ (M), $g$ (g), $l$ (l) は，本来，パラメータですので，ここでは，"Constant" により値を設定し，"MATLAB Function" ("arm_model") に入力しています．もちろん，先に説明したように，手動で Scope（スコープ）のプロパティを「Input（入力）」から「Parameter（パラメータ）」に変更してもかまいません．

そして，M ファイル "arm_pi_d_simulation_MATLAB_Function_auto.m" を実行すると，非線形シミュレーションの結果が表示されます．

7. 実行速度の比較

　アーム系の PI-D 制御の非線形シミュレーションを行い，実行時間の比較を行いました．パソコンのスペックは，以下のとおりです．

• PC: HP ENVY x360 13-ay1000 パフォーマンスモデルG2
• OS: Microsoft Windows 11 Home
• CPU: AMD Ryzen™ 7 5800U
• メモリ: 16GB

　シミュレーションの設定を上記のようにし，1000 回の実行時間を平均しました．そのために，Simulink モデルを開いていない状態で配布する M ファイル

• "tic_toc_Fcn.m"
• "tic_toc_Interpreted_MATLAB_Function.m"
• "tic_toc_MATLAB_Function.m"

を実行しました．得られた結果を以下に示します．Simulink ブロック "Fcn" が最も高速であることがわかります．

実行速度の比較

バージョン	"Fcn"	"Interpreted MATLAB Function"	"MATLAB Function"
R2022b	0.0815 [s]	0.2760 [s]	0.1619 [s]
R2022a	0.0814 [s]	0.2557 [s]	0.1721 [s]
R2018a	0.0379 [s]	0.2604 [s]	0.1251 [s]

8. おわりに

　本記事では，Simulink を利用した非線形シミュレーションの方法について説明しました．私の場合，昔からもっぱら "Fcn" を利用し続けています．"Fcn" は使い方が単純で，コード生成にも対応しているので，実機実験用の Simulink モデルにトレースするのが容易です．

　一方で，"MATLAB Function" では多くの MATLAB 関数を利用できますので，6.2 節で説明したように，Simulink を実行させながらアニメーション表示させたり，Symbolic Math Toolbox と連携ができたりします．

　用途によって，お好みの方法で非線形シミュレーションをしてはいかがでしょうか．

おまけ

　詳細は省略しますが，今回紹介した PI-D 制御ではなく，I-PD 制御（比例・微分先行型 PID 制御）により，実機実験を行ってみました．目標角度が大きいと重力項（非線形項）の線形化誤差の影響で，非線形シミュレーションや実機実験では，I-PD 制御の方が規範モデルよりもオーバーシュートが大きくなっていることがわかります．また，この非線形項をフィードバックで打ち消すような非線形補償を施すことで，理想的には，目標角度を大きくしても規範モデルの応答と一致させることが可能です．実機実験でもオーバーシュートを抑制できています．

参考文献 / 参考資料

1. 遠藤眞覇人：MATLAB Function ブロックを使いこなせ！
2. 川田昌克，西岡勝博：MATLAB/Simulink によるわかりやすい制御工学（第 2 版） (2022) $\cdots\cdots$ サポートページ
3. 川田昌克：MATLAB/Simulink による制御工学入門 (2020) $\cdots\cdots$ サポートページ

---

　

付録：鉛直面を回転するアーム系の PI-D 制御

　PI-D コントローラのゲインは，目標値応答に注目した部分的モデルマッチング法によって設計しています．詳細を知りたい方は文献 2 や文献 3 を参照してください．

　アーム系の伝達関数表現 $(3)$ 式を書き換えると，

\begin{align}
    &
    y(s) = P(s)u(s),\ 
    P(s) = \dfrac{{b}_{0}}{s^2 + {a}_{1}s + {a}_{0}}
    \tag{A.1}
    \\
    &\qquad
    {a}_{1} = \dfrac{Mgl}{J},\ 
    {a}_{0} = \dfrac{c}{J},\ 
    {b}_{0} = \dfrac{1}{J}
\end{align}

となります．一方，PI-D コントローラ $(1)$ 式をラプラス変換すると，

\begin{align}
    u(s) &= {k}_{\rm P}e(s) + \dfrac{{k}_{\rm I}}{s}e(s) - {k}_{\rm D}sy(s)
    \tag{A.2} \\
    &= {C}_{1}(s)r(s) - {C}_{1}(s)y(s),\ 
    \left\{\begin{array}{l}
        {C}_{1}(s) = {k}_{\rm P} + \dfrac{{k}_{\rm I}}{s} + {k}_{\rm D}
        \\
        {C}_{2}(s) = {k}_{\rm P} + \dfrac{{k}_{\rm I}}{s}
    \end{array}\right.
\end{align}

となります．PI-D コントローラは，微分先行型 PID コントローラとも呼ばれます．

　目標値 $r(s)$ から制御出力 $y(s)$ までの伝達関数は

\begin{align}
    {G}_{yr}(s) &= \dfrac{P(s){C}_{2}(s)}{1 + P(s){C}_{1}(s)}
    \\
    &= \dfrac{\dfrac{{b}_{0}}{s^2 + {a}_{1}s + {a}_{0}}
                \biggl({k}_{\rm P} + \dfrac{{k}_{\rm I}}{s}\biggr)}
             {1 + \dfrac{{b}_{0}}{s^2 + {a}_{1}s + {a}_{0}}
                \biggl({k}_{\rm P} + \dfrac{{k}_{\rm I}}{s} + {k}_{\rm D}s\biggr)}
    \\
    &= \dfrac{{b}_{0}{k}_{\rm P}s + {b}_{0}{k}_{\rm I}}
            {s^3 + ({a}_{1} + {b}_{0}{k}_{\rm D})s^2
                 + ({a}_{0} + {b}_{0}{k}_{\rm P})s
                 + {b}_{0}{k}_{\rm I}}
    \tag{A.3}
\end{align}

となります．一方，理想的な応答波形となる $2$ 次の規範モデルの伝達関数を

\begin{align}
    {M}_{2}(s) = \dfrac{{\omega}_{\rm m}^{2}}
            {s^2 + {\alpha}_{1}{\omega}_{\rm m}s + {\omega}_{\rm m}^{2}}
    \tag{A.4}
\end{align}

とします．このとき，${G}_{yr}(s)$ の逆数をマクローリン展開した

\begin{align}
    \dfrac{1}{{G}_{yr}(s)} = 1 + {\gamma}_{1}s
         + {\gamma}_{2}s^2
         + {\gamma}_{3}s^3
         + \cdots
    \tag{A.5}
\end{align}

と ${M}_{2}(s)$ の逆数

\begin{align}
    \dfrac{1}{{M}_{2}(s)} = 1 + \dfrac{{\alpha}_{1}}{{\omega}_{\rm m}}s
                        + \dfrac{1}{{\omega}_{\rm m}^{2}}s^2
                        + 0 \cdot s^3
    \tag{A.6}
\end{align}

が $3$ 次項まで一致するようにコントローラゲイン $k_{\rm P}$, $k_{\rm I}$, $k_{\rm D}$ を決定します．

　以上のことを行う M ファイルを以下に示します．

M ファイル "arm_pi_d_design.m"

clear
format compact

disp(' ')
disp('=====================================================')
disp(' 目標値応答に注目したアーム系の PI-D 制御')
disp('=====================================================')

syms s
syms a0 a1 b0 positive
syms kP kI kD positive
syms alpha1 wm positive

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 制御対象 y(s) = P(s)u(s)')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

P  = b0/(s^2 + a1*s + a0)   % P(s)

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ コントローラ u(s) = C2(s)r(s) - C1(s)y(s)')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

C1 = kP + kI/s + kD*s       % C1(s)
C2 = kP + kI/s              % C2(s)

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ Gyr(s) = P(s)*C2(s)/(1 + P(s)*C1(s))')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

Gyr = P*C2/(1 + P*C1);
Gyr = collect(Gyr,s)        % 降べきの順

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 1/Gyr(s) をマクローリン展開')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 1/Gyr(s) = gamma0 + gamma1*s ')
disp('+                   + gamma2*s^2 + gamma3*s^3 + ...  ')
disp('+ gamma = [ gamma0')
disp('+           gamma1')
disp('+           gamma2')
disp('+           gamma3 ] ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

inv_Gyr = taylor(1/Gyr,s,0,'Order',4)
gamma = coeffs(expand(inv_Gyr),s)';
gamma = gamma(1:4)

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 2 次の規範モデル')
disp('+                    wn^2          ')
disp('+ M2(s) = ------------------------')
disp('+          s^2 + alpha1*wn*s + wn^2')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

M2 = wm^2/(s^2 + alpha1*wm*s + wm^2)

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 逆数 1/M2(s)')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 1/M2(s) = gamma_m0 + gamma_m1*s  ')
disp('+                     + gamma_m2*s^2')
disp('+ gamma_m = [ gamma_m0')
disp('+             gamma_m1')
disp('+             gamma_m2')
disp('+             0        ] ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

gamma_m = coeffs(1/M2,s)';
gamma_m = [gamma_m; 0]

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 設計された PID パラメータ（gamma = gamma_m の解）')
disp('+ kP = sol_kP, kI = sol_kI, kD = sol_kD')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

sol = solve(gamma(2:4)-gamma_m(2:4),[kI kP kD], 'ReturnConditions', true);

sol_kI = sol.kI
sol_kP = sol.kP
sol_kD = sol.kD

% sol.conditions

disp(' ')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')
disp('+ 設計された PID パラメータを用いたときの Gyr(s)')
disp('+++++++++++++++++++++++++++++++++++++++++++++++++++++')

Gyr = subs(Gyr,[kI kP kD],[sol_kI sol_kP sol_kD]);
Gyr = collect(Gyr,s)

M ファイル "arm_pi_d_design.m" の実行結果を以下に示します．

M ファイル "arm_pi_d_design.m" の実行結果

>> arm_pi_d_design
 
=====================================================
 目標値応答に注目したアーム系の PI-D 制御
=====================================================
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 制御対象 y(s) = P(s)u(s)
+++++++++++++++++++++++++++++++++++++++++++++++++++++
P =
b0/(s^2 + a1*s + a0)
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ コントローラ u(s) = C2(s)r(s) - C1(s)y(s)
+++++++++++++++++++++++++++++++++++++++++++++++++++++
C1 =
kP + kD*s + kI/s
C2 =
kP + kI/s
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ Gyr(s) = P(s)*C2(s)/(1 + P(s)*C1(s))
+++++++++++++++++++++++++++++++++++++++++++++++++++++
Gyr =
(b0*kP*s + b0*kI)/(s^3 + (a1 + b0*kD)*s^2 + (a0 + b0*kP)*s + b0*kI)
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 1/Gyr(s) をマクローリン展開
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 1/Gyr(s) = gamma0 + gamma1*s 
+                   + gamma2*s^2 + gamma3*s^3 + ...  
+ gamma = [ gamma0
+           gamma1
+           gamma2
+           gamma3 ] 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
inv_Gyr =
(1/(b0*kI) - kP^3/kI^3 - (kP*(a1 + b0*kD))/(b0*kI^2) + (kP^2*(a0 + b0*kP))/(b0*kI^3))*s^3 + (kP^2/kI^2 + (a1 + b0*kD)/(b0*kI) - (kP*(a0 + b0*kP))/(b0*kI^2))*s^2 + ((a0 + b0*kP)/(b0*kI) - kP/kI)*s + 1
gamma =
                                                                 1
                                                        a0/(b0*kI)
                            kD/kI + a1/(b0*kI) - (a0*kP)/(b0*kI^2)
1/(b0*kI) - (kD*kP)/kI^2 + (a0*kP^2)/(b0*kI^3) - (a1*kP)/(b0*kI^2)
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 2 次の規範モデル
+                    wn^2          
+ M2(s) = ------------------------
+          s^2 + alpha1*wn*s + wn^2
+++++++++++++++++++++++++++++++++++++++++++++++++++++
M2 =
wm^2/(s^2 + alpha1*s*wm + wm^2)
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 逆数 1/M2(s)
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 1/M2(s) = gamma_m0 + gamma_m1*s  
+                     + gamma_m2*s^2
+ gamma_m = [ gamma_m0
+             gamma_m1
+             gamma_m2
+             0        ] 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
gamma_m =
        1
alpha1/wm
   1/wm^2
        0
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 設計された PID パラメータ（gamma = gamma_m の解）
+ kP = sol_kP, kI = sol_kI, kD = sol_kD
+++++++++++++++++++++++++++++++++++++++++++++++++++++
sol_kI =
(a0*wm)/(alpha1*b0)
sol_kP =
wm^2/b0
sol_kD =
(alpha1^2*wm^2 - a1*alpha1*wm + a0)/(alpha1*b0*wm)
 
+++++++++++++++++++++++++++++++++++++++++++++++++++++
+ 設計された PID パラメータを用いたときの Gyr(s)
+++++++++++++++++++++++++++++++++++++++++++++++++++++
Gyr =
wm^2/(s^2 + alpha1*s*wm + wm^2)

なお，このようにコントローラゲイン $k_{\rm P}$, $k_{\rm I}$, $k_{\rm D}$ を選ぶと，$G_{yr}(s)$ は極零相殺され，厳密に $M_{2}(s)$ と一致します．