【Python】なるべく短くベジェ曲線

ベジェ曲線の定義

制御点$P_0,...,P_{N-1}$が与えられたとき，

P(t)=\sum_{i=0}^{N-1}P_i\left(\begin{array}{c}n\\ i\\ \end{array}\right)t^i(1-t)^{n-i}\\
\mathrm{where} \quad t \in [0, 1]

簡単そう．

書く

import numpy as np

def Bezier(p, t):
    *_, n = p.shape
    J = np.vectorize(lambda i, t: (n/np.r_[1:i+1]-1).prod() * t**i * (1-t)**(n-1-i), signature='(),(m)->(m)')
    return p @ J(np.r_[:n], t)

書いた．

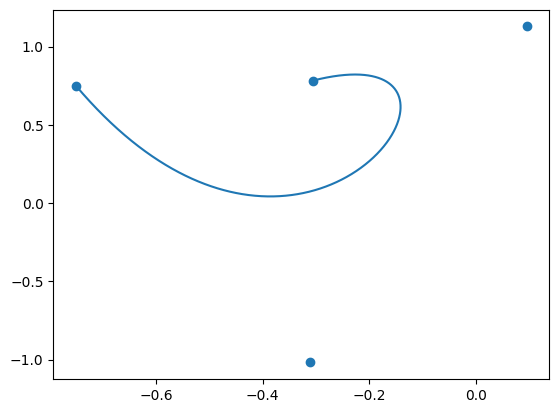
使ってみる

import matplotlib.pyplot as plt

n = 4 # 3次ベジェ曲線
t = np.linspace(0, 1, 1000)
p = np.random.randn(2, n).cumsum(0) # 制御点
plt.scatter(*p) # 制御点をプロット
plt.plot(*Bezier(p, t)) # ベジェ曲線をプロット
plt.show()

良さそう．

import matplotlib.pyplot as plt
fig, ax = plt.subplots(subplot_kw={'projection': '3d'})

n = 4 # 3次ベジェ曲線
t = np.linspace(0, 1, 1000)
p = np.random.randn(3, n).cumsum(0) # 制御点
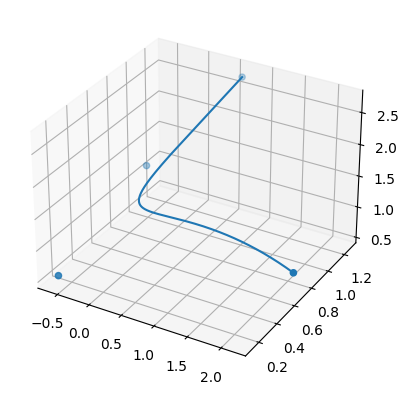
ax.scatter(*p) # 制御点をプロット
ax.plot(*Bezier(p, t)) # ベジェ曲線をプロット
plt.show()

次元上げても使えそう．

import matplotlib.pyplot as plt

n = 4 # 3次ベジェ曲線
num = 10 # 本数
t = np.linspace(0, 1, 1000)
p = np.random.randn(num, 2, n).cumsum(1) # 制御点
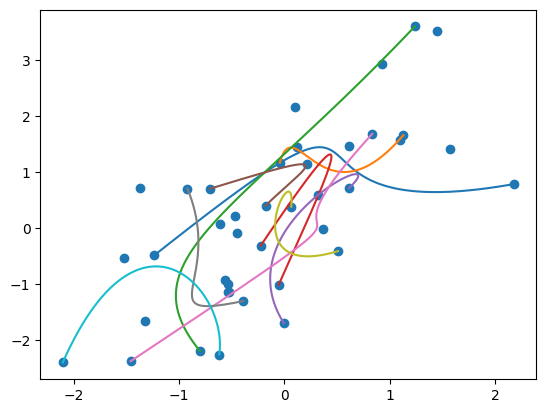
plt.scatter(*p.transpose(1, 2, 0)) # 制御点をプロット
plt.plot(*Bezier(p, t).transpose(1, 2, 0)) # ベジェ曲線をプロット
plt.show()

複数本同時でも．