【Python】格子ボルツマン法でカルマン渦を観察しよう。【流体シミュレーション】

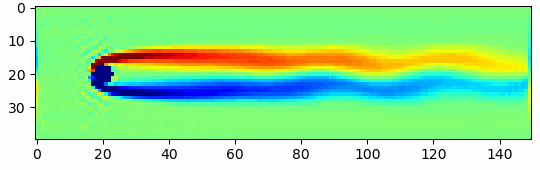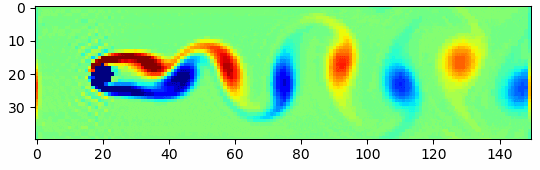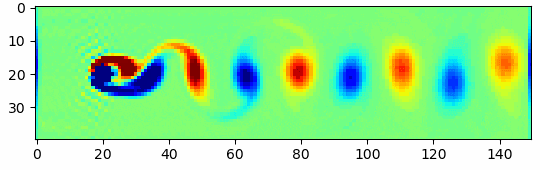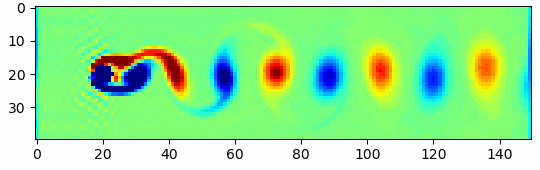
#はじめに

今回は格子ボルツマン法を用いて上のgifのような流体シミュレーションをしてみたいと思います。

**格子ボルツマン法とは**

>格子ボルツマン法（こうしボルツマンほう）とは、流体を多数の仮想粒子の集合体（格子気体モデル）で近似し、各粒子の衝突と並進とを粒子の速度分布関数を用いて逐次発展させることにより、そのモーメントを計算することによって、流体の熱流動場を求めるシミュレーション法のことである。　-Wikipedia

また、今回もできるだけ短くなるように書いたところ、案の定参考サイト（記事の最後にリンクあります）に載っているサンプルコードより遅くなりました。行列計算が早いNumpyといえど頼り過ぎはだめみたいです。

#方法
ここでは詳しい理論は省略して、実装に必要な内容を解説します。

計算する式を始めに示しておきます。

n_i'(r,t+1)=n_i(r+e_i,t)\tag{1}\\

n_i(r,t+1) = (1-\omega)n_i'(r,t+1)+\omega\bigg[\rho w_i(1+3\vec{e_i}\cdot\vec{u}+\frac{9}{2}(\vec{e_i}\cdot\vec{u})^2-\frac{3}{2}|\vec{u}|^2)\bigg] \tag{2}

ここで、\\
n_i は粒子分布関数の i 成分、\\
\vec{e_i} は i 番目の位置ベクトル、\\
w_i=\begin{cases}
    \frac{4}{9} & ( i = 0 ) \\
    \frac{1}{9} & ( 1\le i \le 4 )\\
    \frac{1}{36} & (5 \le i \le 8)
\end{cases}\\
\rho =\sum_{i} n_i(t)\\
\vec{u} は二次元の場合 x, y 2方向の速度ベクトル、\\
\omega = 1/\tau ， \tau は単一時間緩和係数です。

これを各 $i$ 、各地点について計算します。

まず、 $\vec e_i$ ですがこれは自分のマスを原点としたときの自分のマス＋隣接する8マスに向かう位置ベクトルで、
$i=0$ が自分のマス $\vec e_0=(0, 0)$、
$1\le i\le 4$ が上下左右 $\vec e_{1...4}=(0,1),(0,-1),(1,0),(-1,0)$、
$5\le i\le 8$ がナナメに隣り合っているマス $\vec e_{5...8}=(1,1),(-1,-1),(1,-1),(-1,1)$
を表します。
ですので、$(1)$式は隣接マスからの流入を表していると解釈できますね。

次に $\vec e_i \cdot \vec u$ です。
$\vec u=(u_x,u_y)$ ですので、例えば $i=7$ であれば、
$\vec e_7 \cdot \vec u = (1,-1)\cdot (u_x,u_y) = u_x-u_y$
となります。

最後に $|u|^2$ 、
これは$\vec u$ の長さの2乗ですので、
$|u|^2=u_x^2+u_y^2$ です。

#障害物の処理
ただ流れるだけではあまり面白くない上、本題のカルマン渦が発生しないので、障害物を設置した際の処理についても考えましょう。
ただ、これについては格子ボルツマン法の場合簡単で(ナヴィエ・ストークス方程式を近似計算したときは少し面倒だった気がする)、
もともと流入方向ごとに分けて計算しているので、障害物に当たったら流入方向と逆の成分に流してやれば済みます。

ではそろそろ実装と行きましょう。

#実装
###関数の定義

Lattice_Boltzmann_Method.py

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from ipywidgets import interact


w = np.array([4 / 9, 1 / 9, 1 / 9, 1 / 9, 1 / 9, 1 / 36, 1 / 36, 1 / 36, 1 / 36])
e = np.array([[0, 0], [0, 1], [0, -1], [1, 0], [-1, 0], [1, 1], [-1, -1],[1, -1], [-1, 1]])


def stream(): #(1)式＋障害物との衝突処理
    global n
    for i, axis in zip(range(1, 5),[[1, 1, 0, 1], [1, -1, 0, -1], [0, 1, 1, -1], [0, -1, 1, 1]]): #(1)式
        n[:, :, i] = np.roll(n[:, :, i], axis[1], axis=axis[0])
        n[:, :, i + 4] = np.roll(np.roll(n[:, :, i + 4], axis[1],axis=axis[0]),axis[3],axis=axis[2])
    for i in range(1, 9):
        n[:, :, i][barrier[:, :, i]] = n[:, :, i - (-1)**i][barrier[:, :, 0]] #衝突した分を逆向きの成分に流してます。


def collide(): #(2)式＋左端からの流入
    global n, u, u9
    rho = n.sum(axis=2).reshape(H, W, 1) #ρの計算
    u = (n @ e) / rho #(ux,uy)の計算
    n = (1 - om) * n + om * w * rho * (1 - 1.5 *(u**2).sum(axis=2).reshape(H, W, 1) +3 * (u @ e.T) + 4.5 * (u @ e.T)**2) #(2)式
    n[:, 0] = w * (1 - 1.5 * (u_o**2).sum(axis=1).reshape(H, 1) + 3 *(u_o @ e.T) + 4.5 * (u_o @ e.T)**2) #左端からの流入


def curl(): #プロットする際の色に関係してる関数
    return np.roll(u[:, :, 0], -1, axis=1) - np.roll(u[:, :, 0], 1, axis=1) - np.roll(u[:, :, 1], -1, axis=0) + np.roll(u[:, :, 1], 1, axis=0)


def mk_barrier(arr): #障害物を表現した配列を渡すと衝突時の跳ね返り先の対応関係などを計算してくれる子
    global barrier
    barrier = np.zeros((H, W, 9), bool)
    barrier[:, :, 0] = arr
    for i, axis in zip(range(1, 5),[[1, 1, 0, 1], [1, -1, 0, -1], [0, 1, 1, -1], [0, -1, 1, 1]]):
        barrier[:, :, i] = np.roll(barrier[:, :, 0], axis[1], axis=axis[0])
        barrier[:, :, i + 4] = np.roll(barrier[:, :, i], axis[3], axis=axis[2])

###パラメータの定義、初期化

Lattice_Boltzmann_Method.py

H, W = 40, 100 #タテ・ヨコ

viscosity = .005 #粘度
om = 1 / (3 * viscosity + 0.5) #参考サイトに倣ってこの計算になっています。粘度とωの関係式らしい。

u0 = [0, .12] #初速兼左端からの流入の速度ベクトル(-uy,ux)に対応
u = np.ones((H, W, 2)) * u0
u_o = np.ones((H, 2)) * u0
n = w * (1 - 1.5 * (u**2).sum(axis=2).reshape(H, W, 1) + 3 * (u @ e.T) + 4.5 * (u @ e.T)**2)

###障害物

Lattice_Boltzmann_Method.py

r = 3 #壁の長さとか円の半径とか

#壁
wall = np.zeros((H, W), bool)
wall[H // 2 - r:H // 2 + r, H // 2] = True

#円
x, y = np.meshgrid(np.arange(W), np.arange(H))
circle = ((x - H / 2)**2 + (y - H / 2)**2 <= r**2)

mk_barrier(circle)

###プロット

Lattice_Boltzmann_Method.py

def update(i):
    for t in range(10):
        stream()
        collide()
    im.set_array(curl() - barrier[:, :, 0])
    return im,

"""Jupyter用　インタラクティブになる
@interact(Viscosity=(0.05, 2.0, 0.01),v0=(0, 0.12, 0.01),Barrier=["circle", "wall"])
def a(Viscosity, v0, Barrier):
    global viscosity, om, u0, u_o
    viscosity = Viscosity * .1
    om = 1 / (3 * viscosity + 0.5)
    u0 = [0, v0]
    u_o = np.ones((H, 2)) * u0
    mk_barrier(eval(Barrier))
"""

fig = plt.figure()
stream()
collide()
im = plt.imshow(curl() - barrier[:, :, 0],cmap="jet",norm=plt.Normalize(-.1, .1))
anim = FuncAnimation(fig, update, interval=1, blit=True)
plt.show()

#結果
冒頭に示したものと同じですが、

#まとめ
自然現象を自分で書いたコードで再現できると感動しますよね。
皆さんも是非試してみてください。

全コードツナゲターノ

Lattice_Boltzmann_Method.py

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from ipywidgets import interact


w = np.array([4 / 9, 1 / 9, 1 / 9, 1 / 9, 1 / 9, 1 / 36, 1 / 36, 1 / 36, 1 / 36])
e = np.array([[0, 0], [0, 1], [0, -1], [1, 0], [-1, 0], [1, 1], [-1, -1],[1, -1], [-1, 1]])


def stream(): #(1)式＋障害物との衝突処理
    global n
    for i, axis in zip(range(1, 5),[[1, 1, 0, 1], [1, -1, 0, -1], [0, 1, 1, -1], [0, -1, 1, 1]]): #(1)式
        n[:, :, i] = np.roll(n[:, :, i], axis[1], axis=axis[0])
        n[:, :, i + 4] = np.roll(np.roll(n[:, :, i + 4], axis[1],axis=axis[0]),axis[3],axis=axis[2])
    for i in range(1, 9):
        n[:, :, i][barrier[:, :, i]] = n[:, :, i - (-1)**i][barrier[:, :, 0]] #衝突した分を逆向きの成分に流してます。


def collide(): #(2)式＋左端からの流入
    global n, u, u9
    rho = n.sum(axis=2).reshape(H, W, 1) #ρの計算
    u = (n @ e) / rho #(ux,uy)の計算
    n = (1 - om) * n + om * w * rho * (1 - 1.5 *(u**2).sum(axis=2).reshape(H, W, 1) +3 * (u @ e.T) + 4.5 * (u @ e.T)**2) #(2)式
    n[:, 0] = w * (1 - 1.5 * (u_o**2).sum(axis=1).reshape(H, 1) + 3 *(u_o @ e.T) + 4.5 * (u_o @ e.T)**2) #左端からの流入


def curl(): #プロットする際の色に関係してる関数
    return np.roll(u[:, :, 0], -1, axis=1) - np.roll(u[:, :, 0], 1, axis=1) - np.roll(u[:, :, 1], -1, axis=0) + np.roll(u[:, :, 1], 1, axis=0)


def mk_barrier(arr): #障害物を表現した配列を渡すと衝突時の跳ね返り先の対応関係などを計算してくれる子
    global barrier
    barrier = np.zeros((H, W, 9), bool)
    barrier[:, :, 0] = arr
    for i, axis in zip(range(1, 5),[[1, 1, 0, 1], [1, -1, 0, -1], [0, 1, 1, -1], [0, -1, 1, 1]]):
        barrier[:, :, i] = np.roll(barrier[:, :, 0], axis[1], axis=axis[0])
        barrier[:, :, i + 4] = np.roll(barrier[:, :, i], axis[3], axis=axis[2])


H, W = 40, 100 #タテ・ヨコ

viscosity = .005 #粘度
om = 1 / (3 * viscosity + 0.5) #参考サイトに倣ってこの計算になっています。粘度とωの関係式らしい。

u0 = [0, .12] #初速兼左端からの流入の速度ベクトル(-uy,ux)に対応
u = np.ones((H, W, 2)) * u0
u_o = np.ones((H, 2)) * u0
n = w * (1 - 1.5 * (u**2).sum(axis=2).reshape(H, W, 1) + 3 * (u @ e.T) + 4.5 * (u @ e.T)**2)


r = 3 #壁の長さとか円の半径とか

#壁
wall = np.zeros((H, W), bool)
wall[H // 2 - r:H // 2 + r, H // 2] = True

#円
x, y = np.meshgrid(np.arange(W), np.arange(H))
circle = ((x - H / 2)**2 + (y - H / 2)**2 <= r**2)

mk_barrier(circle)


def update(i):
    for t in range(10):
        stream()
        collide()
    im.set_array(curl() - barrier[:, :, 0])
    return im,

"""Jupyter用　インタラクティブになる
@interact(Viscosity=(0.05, 2.0, 0.01),v0=(0, 0.12, 0.01),Barrier=["circle", "wall"])
def a(Viscosity, v0, Barrier):
    global viscosity, om, u0, u_o
    viscosity = Viscosity * .1
    om = 1 / (3 * viscosity + 0.5)
    u0 = [0, v0]
    u_o = np.ones((H, 2)) * u0
    mk_barrier(eval(Barrier))
"""

fig = plt.figure()
stream()
collide()
im = plt.imshow(curl() - barrier[:, :, 0],cmap="jet",norm=plt.Normalize(-.1, .1))
anim = FuncAnimation(fig, update, interval=1, blit=True)
plt.show()

##参考 [Fluid Dynamics Simulation](http://physics.weber.edu/schroeder/fluids/)