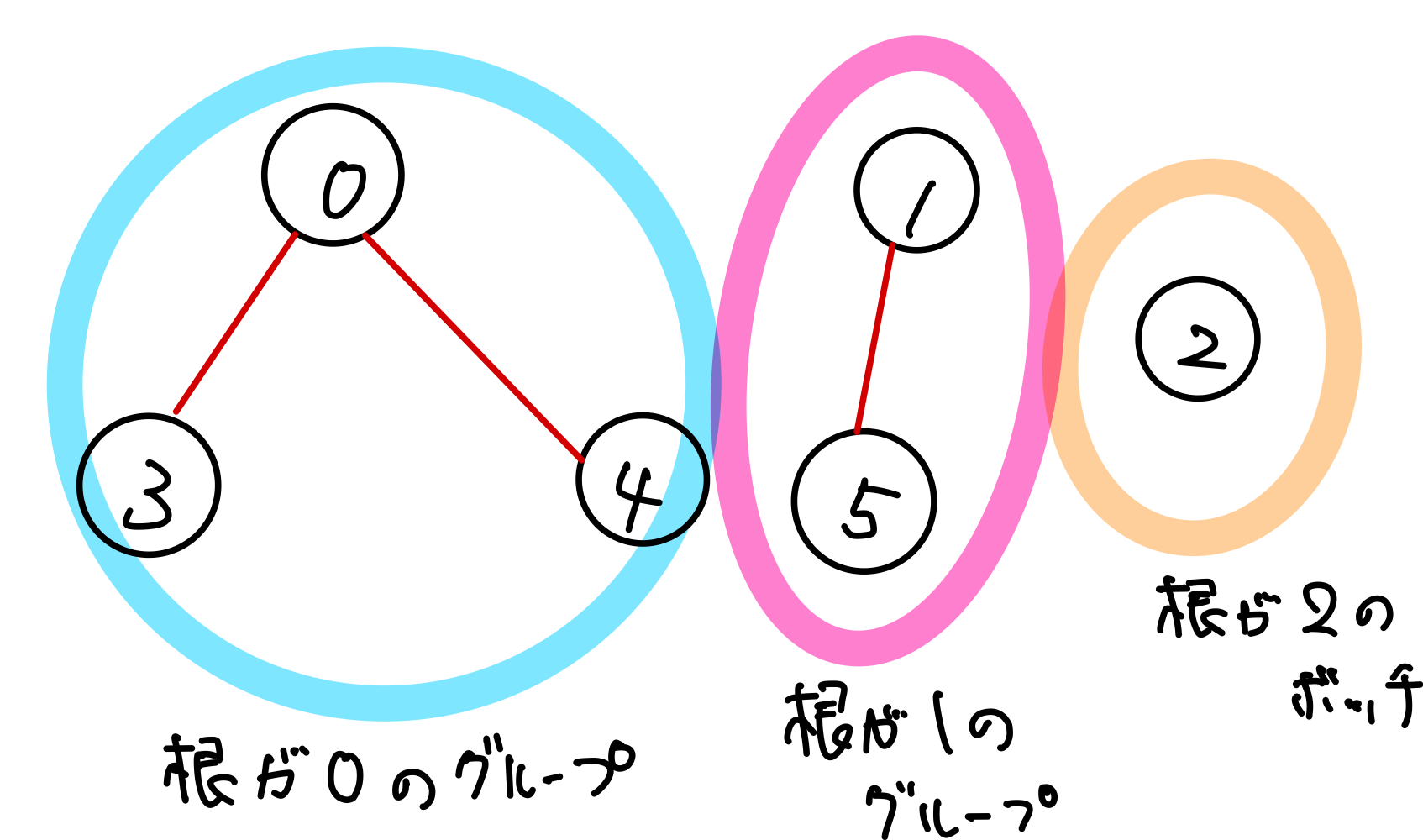Union-Find木
Atcoder典型90 問12の勉強中。解説記事や参考プログラムを参考にさせていただきました。
木構造の種類の1つでグループ分けに用いる
AさんとBさんが同じグループかどうかを高速で計算できる
pythonコード(コメント文なし)
class UnionFind():
def __init__(self, max_size:int):
self.parent = [i for i in range(max_size)]
def root(self, id):
if self.parent[id] == id:
return id
else:
self.parent[id] = self.root(self.parent[id])
return self.parent[id]
def linking(self, id1, id2):
if self.root(id1) == self.root(id2):
return
else:
self.parent[self.parent[id2]] = self.parent[id1]
def chk_link(self, id1, id2):
if self.root(id1) == self.root(id2):
return True
else:
return False
pythonコード(コメント文あり)
class UnionFind():
"""
parameter
max_size : 最大ノード数を指定
method
root : 自分の親ノードをたどって根を調べる。
このとき調べたノードは根が親になるようにつなぎなおす
linking : 2つのidが所属するグループを結合する
chk_link : 2つのidが同じグループに所属しているかをチェック
"""
def __init__(self, max_size:int):
# 各ノードの親を入れるリストを用意する
# 初期の親は自分自身になるように設定
self.parent = [i for i in range(max_size)]
# 自分の根が誰であるかをチェックするメソッド
def root(self, id):
# 自分の親が自分である場合は、自分自身のIDを返す
# ひとりボッチか、自分がみんなの親である場合がこれ
if self.parent[id] == id:
return id
# 親が自分自身でない場合は、親をたどって根を調べる
# この時再帰呼び出しを利用して、調べたノードの親が根になるように繋ぎなおす
# これで何度も何度も親をたどって根を調べる必要がなくなる
else:
self.parent[id] = self.root(self.parent[id])
return self.parent[id]
# 新たな結合を定義する
def linking(self, id1, id2):
# id1とid2の根が同じなら、繋ぎなおす必要がないので、終了
# self.rootを使って、id1, id2の根を調べることで、id1,id2の親が根になっている
if self.root(id1) == self.root(id2):
return
else:
# id2の根の親がid1の根になるように繋ぎなおす
# 根をつなぎ変えることで、子供たち全部の根が変わる
# if文はなくてもいいが、root()をしないと、グループ全体の繋ぎ変えにならないので注意
self.parent[self.parent[id2]] = self.parent[id1]
# 2つのIDが同じグループに入っているかを確認
def chk_link(self, id1, id2):
# id1, id2の根を調べて、一致していれば同じグループ
if self.root(id1) == self.root(id2):
return True
else:
return False
-
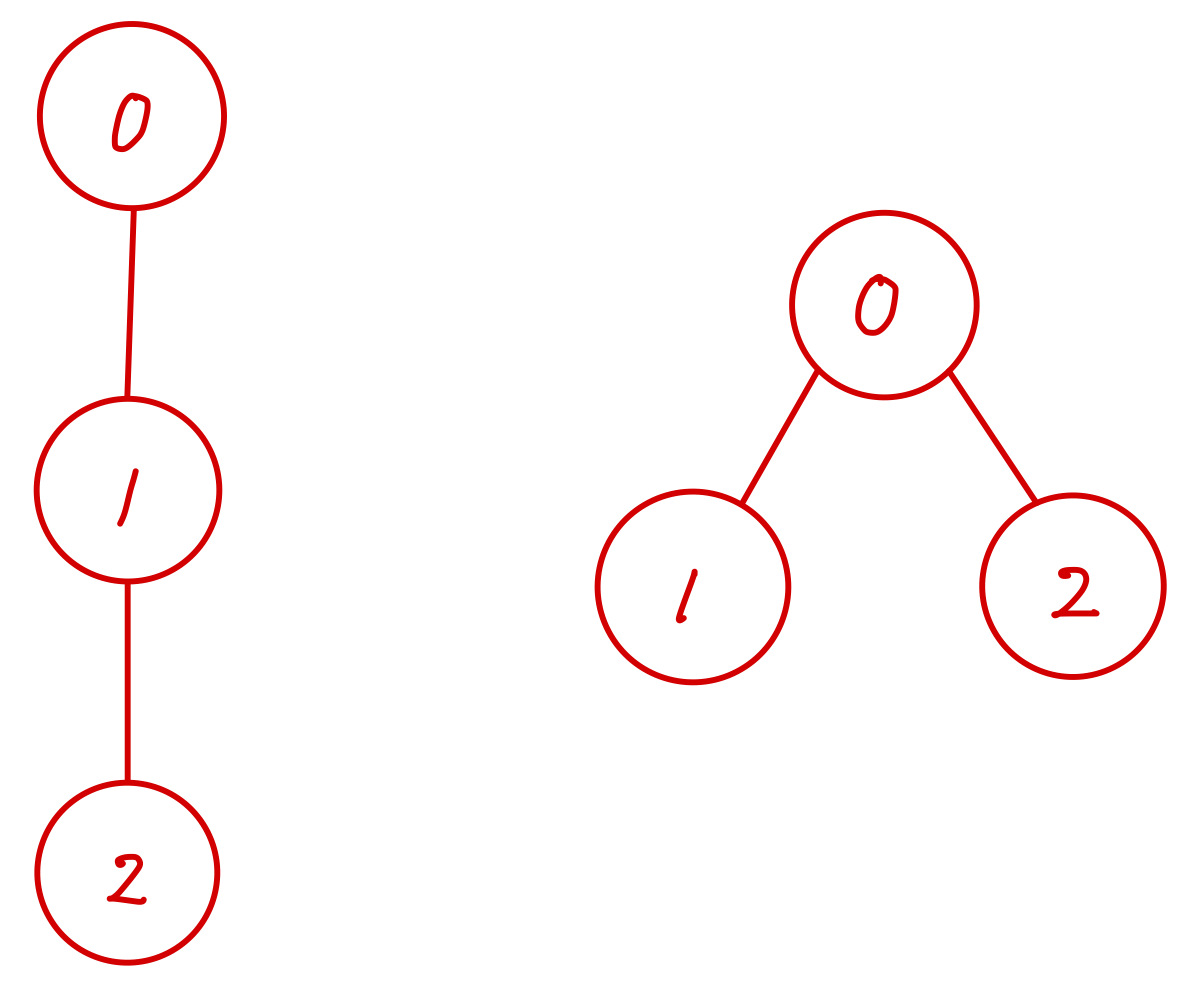
木構造が上図の左の形になっている場合
parent = [0, 0, 1] となっていて、root(2)を実行すると、- root(2)
parent[2] = 1 で 親が自分自身でないので、再度root()を呼び出すことになる。
この時引数は親である"1"になる - root(1)
parent[1] = 0 でも同様で、root(0)が呼び出される。 - root(0)
parent[0] = 0 で親が自分自身なので、自分のid=0を返す。👈このグループの根が0と分かる - root(1)に帰ってきて
parent[1] = 0(根) 親に根を設定 - root(2)に帰ってきて
parent[0] = 0(根) 親に根を設定
以上によって、各ノードの親が根になって、上図右のようになる。
- root(2)
-
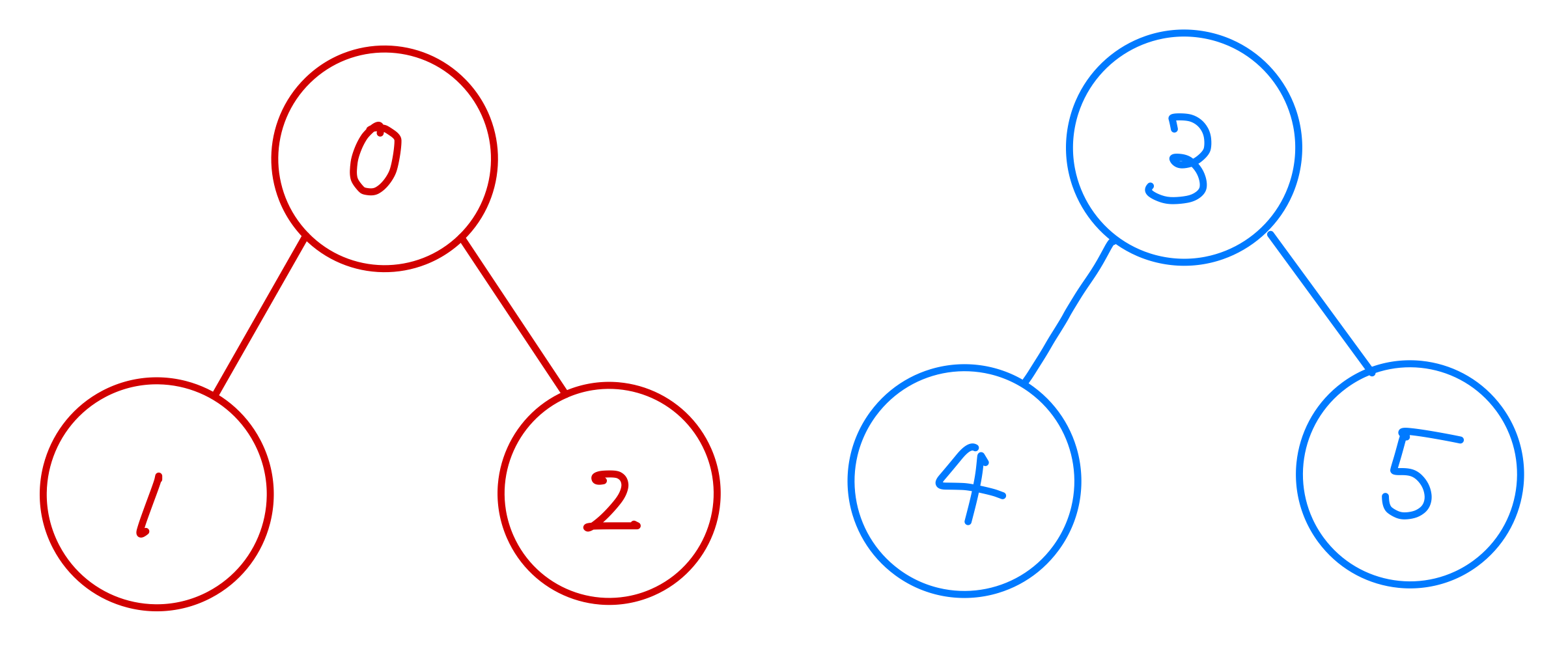
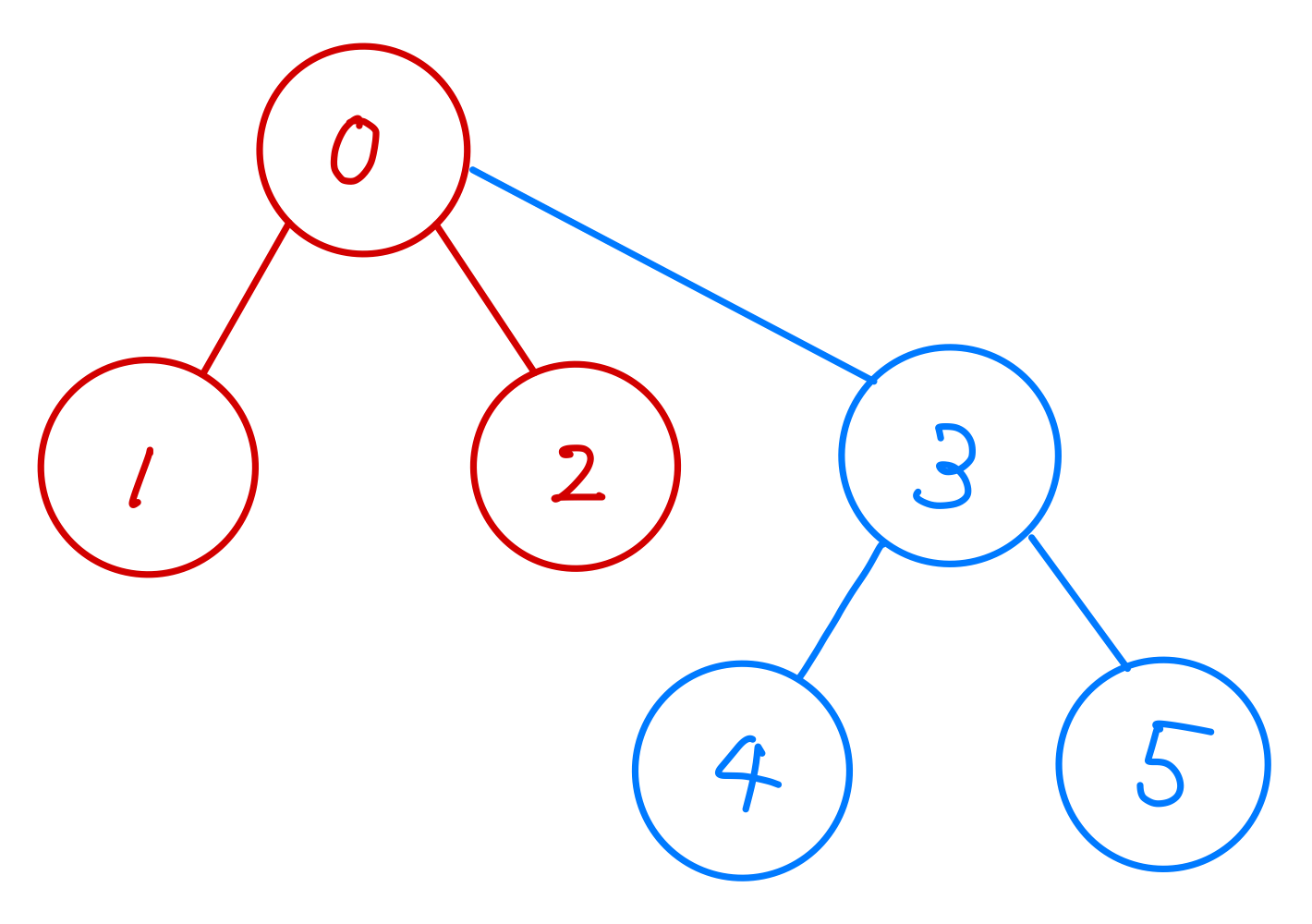
method : linking()
上図の状態でlinking(2, 4)が実行されたとする
もし、直接根に繋がってなかった場合も、if文のところでroot()をしているので、親が根になるように繋ぎ変えられる。
self.parent[self.parent[id2]] = self.parent[id1]
4の根の親(つまり3の親)が、2の根(つまり1)になるように書き換えることで、
下図のように繋ぎ変えられる。
使い方
linking()で順番に連結させ、chk_link()で2点間が結合しているかを確認する
>>> uf = UnionFind(6)
>>> uf.parent
[0, 1, 2, 3, 4, 5] <= 最初は自分自身が親
>>> uf.linking(1,2) <= 1,2を結合(赤色グループ)
>>> uf.linking(0,1) <= 0,1を結合(赤色グループ)
>>> uf.parent
[0, 0, 1, 3, 4, 5] <= 2の親は1, 1の親は0
>>> uf.root(2) <= 2の根を確認
0
>>> uf.parent
[0, 0, 0, 3, 4, 5] <= 2の親が"0"に変更される
>>> uf.parent
[0, 0, 0, 3, 4, 5]
>>> uf.linking(3,4) <= 3,4を結合(青色グループ)
>>> uf.linking(4,5) <= 4,5を結合(青色グループ)
>>> uf.parent
[0, 0, 0, 3, 3, 3]
>>> uf.chk_link(1,5)
False <= 1,5は別々のグループなのでFalse
>>> uf.linking(2,4) <= 赤グループの2と青グループの4を結合
>> uf.parent
[0, 0, 0, 0, 3, 3] <=4,5の親は3で、3の親は0になり、グループが結合された
>>> uf.chk_link(1,5)
True <= 1,5は直接結合していないが、同じグループなのでTrueになる
免責事項
コードのコピペは自由ですが、作者は損害等の一切の責任を負いません。