Atcoder ABC学習メモ (python)

• Atcoder ABC学習の自分用メモです。
• 限定公開で書いていましたが、モチベUpのため公開。お汚しすみません。

ABC225-D ~連結管理~

1. 1~Nの車両が存在する
2. Query1では車両xとyを連結、Query2では車両xとyを切り離す
3. Query3で指定された車両が含まれる連結された車両群の車両数と各車両を前から順に書き出す

point

• 各車両について、前後連結車両を管理してあげれば良い

N, Q = map(int, input().split())
qs = [list(map(int, input().split())) for _ in range(Q)]

# 自分のfront, rearの車両を管理するリスト。結合先がない場合は−1
front_car = [-1] * N
rear_car= [-1] * N

for q in qs:
    # x, yを取り出し 配列のIDは0スタートなので-1
    x = q[1] - 1 
    y = q[2] - 1 if len(q) == 3 else 0
  
    # q=1の場合、xのrearはy, yのfrontはx
    if q[0] == 1:
        rear_car[x] = y  
        front_car[y] = x
    # q=2の場合、xのrearとyのfrontを−1に初期化
    if q[0] == 2:
        rear_car[x] = -1
        front_car[y] = -1
    # q=3の場合、前と後ろをたどって車両情報を取得
    if q[0] == 3:
        # 前に辿って車両を調べる
        tmp = x     # 後でxは使うのでtmpに一旦格納   
        ans_f = []  # 前に辿っていった結果を格納
        while tmp > -1: # 連結先が−1つまり、連結されていない場合は終了
            ans_f.append(front_car[tmp]+1)
            tmp = front_car[tmp]
        # 後ろに辿って車両を調べる
        tmp = x
        ans_r = []
        while tmp > -1:
            ans_r.append(rear_car[tmp]+1)
            tmp = rear_car[tmp]
        # 最後の-1はいらないので取り除く
        ans_f = ans_f[:-1]
        ans_r = ans_r[:-1]
        # 前に辿った場合は順番が逆なので入れ替え
        ans_f = ans_f[::-1]
        # 前、自分、後ろを連結
        ans = ans_f + [x+1] + ans_r
        print(len(ans), *ans)

ABC224-D ~9スライドパズル~

1. 9頂点の無向グラフ。頂点は1〜9の数字
2. コマ1~8がどこかの頂点に置かれ、1箇所が空白
3. 空白と隣り合うコマを入れ替えることができる
4. 頂点の数字とコマの数字が同じ＆空白が頂点9にするまでの最小操作回数を答える
5. 答えが存在しない場合は”-1”

9つの数字をスライドするパズルゲームを一般化(入れ替えれる場所を指定)したゲーム

point

• 盤面の状態を頂点としたグラフの探索。最短経路なのでBFSすれば良い
• 訪れたかどうかは辞書型でもっておき、辞書に登録されていれば訪問済み
• 辞書のvalueに深さを設定しておき、辞書[goal]の値が最小操作回数

盤面の形を頂点としてグラフ探索。盤面の形はリストや文字列として定義しておく

"""
Input
5 edgeの数
1 2　edge
1 3
1 9
2 9
3 9
3 9 2 4 5 6 7 8  (コマjが頂点pjにある)
"""

from collections import deque

def main():
    # 読み込み
    M = int(input())
    uv = [list(map(int, input().split())) for _ in range(M)]
    p = list(map(int, input().split()))

    #current pazzle 現在の状態を設定。bが空白
    cp = ["b"]*9
    for i, pi in enumerate(p):
        cp[pi-1] = str(i)

    #edges
    edges = [[] for _ in range(9)]
    for ui, vi in uv:
        edges[ui-1].append(vi-1)
        edges[vi-1].append(ui-1)

    # 空白の場所を保管しておく
    blank_pos = [i for i, pi in enumerate(cp) if pi == "b"][0]

    # queue: 深さ、パズル状態、空白箇所
    queue = deque()
    queue.append((0, cp, blank_pos))

    # 各手順の深さを持つ辞書
    dic_dep = {}
    dic_dep["".join(cp)] = 0

    # BFSで全探索
    while queue:
        depth, cp, blank_pos = queue.popleft()
        for ni in edges[blank_pos]:
            # swap 空白と隣り合う場所を入れ替え
            np = cp.copy()
            np[blank_pos], np[ni] = np[ni], np[blank_pos]
            # 辞書に登録されていれば確認済み
            key = "".join(np)
            if key in dic_dep:
                continue
            # 辞書に深さを登録しqueueに追加
            dic_dep[key] = depth+1
            queue.append((depth+1, np, ni))
            
    GOAL = "01234567b"
    if GOAL in dic_dep:
        return dic_dep[GOAL]
    else:
        return -1

print(main())

ABC224-C ~三角形か直線かの判定~

1. 座標(xi, yi)の節点群が与えられる
2. 3点選んで三角形を作る場合に面積が正になる組み合わせがいくつあるか？
3. 座標は整数で全て異なる点が与えられる

point

• 3点が直線であるか否かを調べれば良い
• 直線である場合以下の式を満たす

dx_{ij} = x_j - x_i\\
dy_{ij} = y_j - y_i\\  
dx_{ik} = x_k - x_i\\  
dy_{ik} = y_k - x_i  

　　とすると傾きが一致していたら直線上にあるので

\frac{dy_{ij}}{dx_{ij}} = \frac{dy_{ik}}{dx_{ik}}\\  
dy_{ij}dx_{ik} = dy_{ik} dx_{ij}  

• ループ数が多いので関数化とPypyで速度改善が見られた
  python(2206ms) → 関数化def main(1364ms) → Pypy(129ms)

N = int(input())
XY = [list(map(int, input().split())) for _ in range(N)]

def main():
  cnt = 0
  #総当たり
  for i in range(N-2):                  #1点目ループ
      for j in range(i+1, N-1):         #2点目ループ
          dx1 = XY[i][0] - XY[j][0]     #1-2点目のxy変化量
          dy1 = XY[i][1] - XY[j][1]
          for k in range(j+1, N):       #3点目ループ
              dx2 = XY[k][0] - XY[j][0] #1-3点目のxy変化量
              dy2 = XY[k][1] - XY[j][1]
              if dx1 * dy2 != dy1 * dx2:#直線でないなら
                  cnt += 1              #cnt += 1
  return cnt
 
print(main())

ABC223-F ~正しい()列とセグメント木~

1. ((()())のような括弧列が与えられる。
2. 正しく開いて閉じていれば正しい括弧列とする。正しい(()), ()()、正しくない))((, ())(
3. L番目とR番目を入れ替えと、任意の区間での括弧列が正しいか否かのQueryが与えられる

point

• ( を +1、 ) を -1として、累積和が0かつ累積和の最小値が0なら正しい括弧列
• セグメント木で累積和と累積和の最小値を一緒に管理する
• セグメント木については、こちらの記事が分かりやすい

N, Q = map(int, input().split())
S = input()
Query = [list(map(int, input().split())) for _ in range(Q)]

# セグメント木
class SegmentTree():
    def __init__(self, n, func, ele, arr):
        """
        n : データ配列サイズ
        func : 演算子
        ele : 単位元
        arr : 初期配列
        """
        
        self.num_leaves = 2**len(bin(n-1)[2:])
        self.arr = [ele] * (self.num_leaves*2)
        self.func = func
        self.ele = ele
        for i in range(n):
            self.arr[self.num_leaves + i - 1] = arr[i]
        for i in range(self.num_leaves-2, 0, -1):
            self.arr[i] = self.func(self.arr[2*i+1], self.arr[2*i+2])
    
    def search(self, i):
        return self.arr[self.num_leaves + i -1]
    
    def update(self, i, val):
        nid = i + self.num_leaves - 1
        self.arr[nid] = val
        while nid:
            nid = (nid - 1) // 2
            cid = nid * 2 + 1
            self.arr[nid] = self.func(*self.arr[cid:cid+2])
    
    def get(self, q_l, q_r, nid=0, node_l=0, depth=0): 
        # nodeの区間を調べる
        node_width = self.num_leaves >> depth
        node_r = node_l + node_width - 1
        # nodeがqの外にあるなら単位元を返す
        if node_l > q_r or node_r < q_l: 
            return self.ele
        # node全体がqには入る場合はnodeの値を返す
        if q_l <= node_l and node_r <= q_r:
            return self.arr[nid]
        # nodeの一部がqに入っている場合は子を探索
        val_l = self.get(q_l, q_r, 2*nid+1, node_l, depth+1)
        val_r = self.get(q_l, q_r, 2*nid+2, node_l+node_width//2, depth+1)

        return self.func(val_l, val_r)
      
# 累積和と累積和の最小を返す関数
def func(a, b):
    # a,bは配列
    return a[0] + b[0], min(a[1], a[0] + b[1])

# ( を +1、) を -1にした配列
s = []
for i, si in enumerate(S):
    val = 1 if si == "(" else -1
    s.append([val, val])  # 二つ管理するのでリスト形式で与える

# セグメント木　累積和と累積和の最小値を管理させる
sg = SegmentTree(N, func, (0,0), s)

for flag, l, r in Query:    
    l -= 1
    r -= 1
    # flag=1なら入れ替え
    if flag == 1:
        s[l], s[r] = s[r], s[l]
        sg.update(l, s[l])
        sg.update(r, s[r])
    else:
        #累積和とその最小値のどちらも0であれば、正しい括弧列
        if sg.get(l, r) == (0, 0):
            print("Yes")
        else:
            print("No")

ABC223-D ~トポロジカルソート~

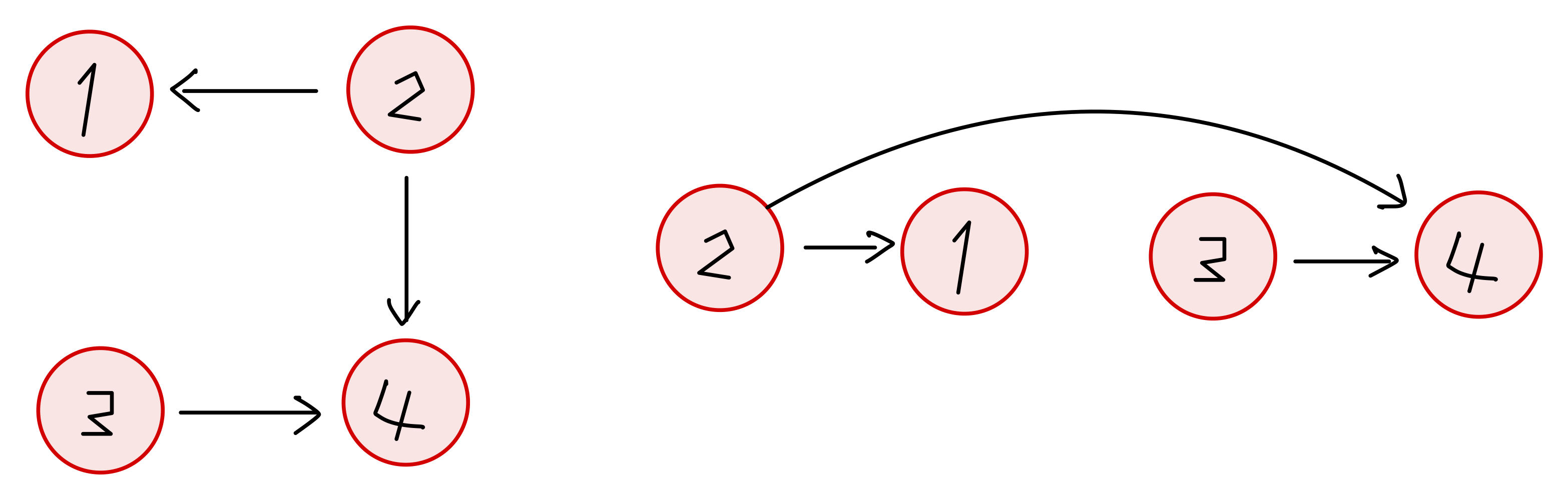
1. 節点ペアについての優先順が与えられる
2. 優先順を守って、辞書順で1番最初となる配列を答える
3. 存在しない場合は”-1”

point

• 各節点について、流入数と流出先をリスト形式で保持する
• 流入数が0つまり、先頭に来られる節点をリストで保持する。今回は辞書順にするためheapqで保持
• 流入数0の節点を一つ選んで確定し、流入数リストと流入数0のリストを更新する
• できたリストの長さを調べて、

# Input
# 4 3
# 2 1
# 3 4
# 2 4

from heapq import heapify, heappush, heappop

N, M = map(int, input().split())
AB = [list(map(int, input().split())) for _ in range(M)]

# 流入数
n_in_num = [0] * N
# 流出先
n_out = [[] for _ in range(N)]

for a, b in AB:
    n_in_num[b-1] += 1
    n_out[a-1].append(b-1)
  
# free node : 流入のない点
free_n = [i for i, num in enumerate(n_in_num) if num == 0]
heapify(free_n)
topo_sort = []
while free_n:
    n = heappop(free_n)
    topo_sort.append(n)
    for m in n_out[n]:
      n_in_num[m] -= 1
      if n_in_num[m] == 0:
        heappush(free_n, m)

if len(topo_sort) == N:
    print(*[i+1 for i in topo_sort])
else:
    print(-1)

ABC219-D ~3次元配列DP~

1. たこ焼きがA個、たい焼きがB個　入ったお弁当がN個ある
2. たこ焼きをX個、たい焼きをY個　食べるには何個最低何個お弁当がいるか？
3. N個全部買っても個数が届かない場合は-1

Point

• ナップサック問題的にDPで解く
• DP[買うか検討したお弁当の個数][たこ焼き数][たい焼き数]
• たこ焼き数はX以上はX、たい焼きはY以上はYとする

# 入力
N = int(input())
X, Y = map(int, input().split())
AB = [list(map(int, input().split())) for _ in range(N)]
AB.sort()

# DP配列作成　お弁当の最小個数が値。途中でminをとるので、初期値は大きな値を入れる。
dp = [[[999]*(Y+1) for _ in range(X+1)] for _ in range(N+1)]

# 3重ループ(今回の問題はN,X,Y ≦ 300)
for ni in range(N):
  a, b = AB[ni]                             # 検討するお弁当の情報
  a, b = min(X, a), min(Y, b)               # XYが上限値
  dp[ni+1][a][b] = 1                        # そのお弁当が1個目の場合
  for xi in range(1, X+1):
    for yi in range(1, Y+1):
      if dp[ni][xi][yi] != 999:             # 初期値でない＝その組み合わせがありうる場合
        na, nb = min(X, xi+a), min(Y, yi+b) # XYが上限値
        dp[ni+1][na][nb] = min(dp[ni+1][na][nb], dp[ni][xi][yi]+1)    # ni番目のお弁当をとる場合
        dp[ni+1][xi][yi] = min(dp[ni+1][xi][yi], dp[ni][xi][yi])      # ni番目のお弁当を取らない場合 
        
ans = dp[-1][-1][-1]   #最後（お弁当全部について検討して、たこたい焼きの個数がXY以上）が答え
if ans == 999:
  print(-1)    # 初期値の場合は達成できないということなので-1
else:
  print(ans)   # 初期値でない場合はその個数を回答

ABC218-E ~最小全域木~

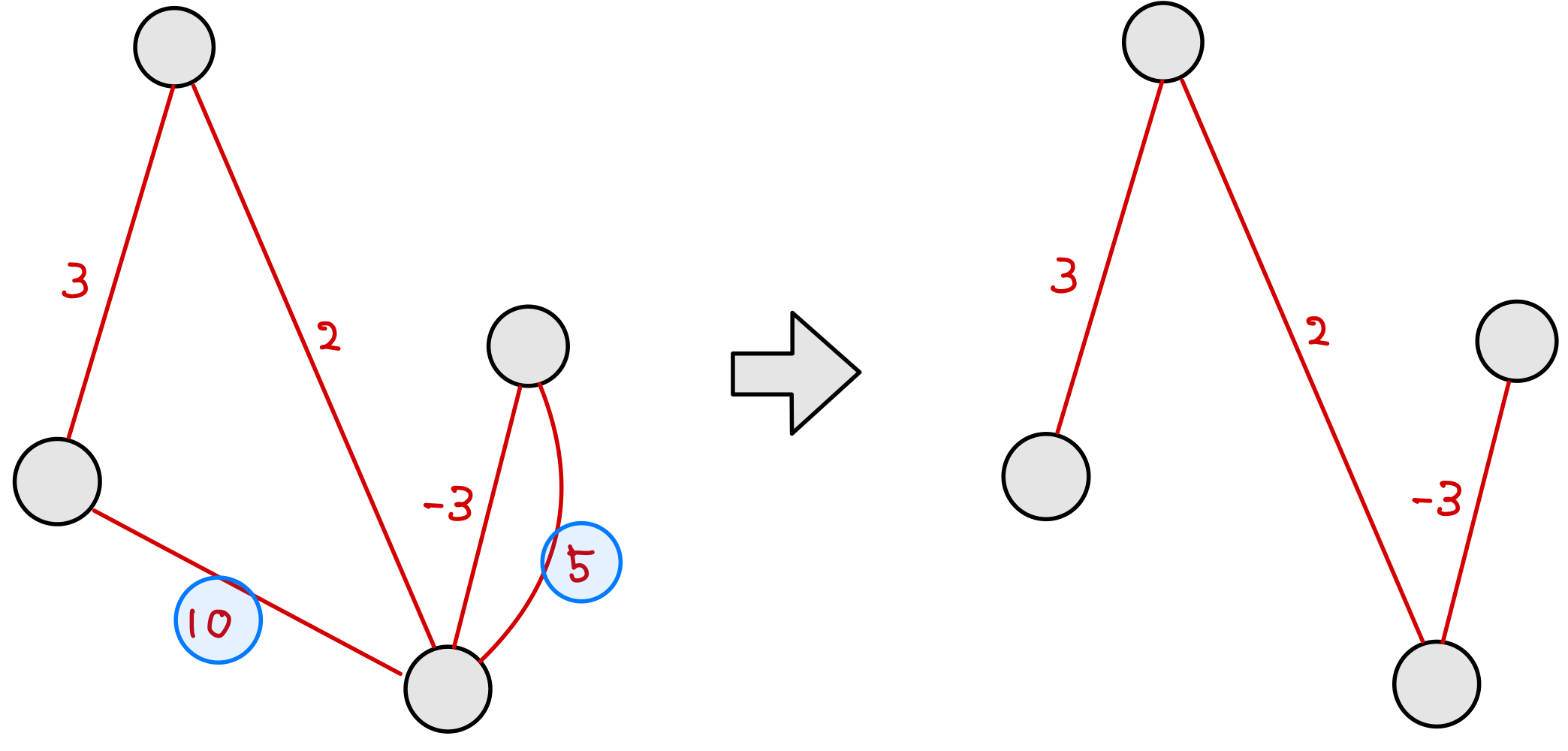
1. 連結グラフから辺を取り去ると、報酬Ciが貰える
2. 連結が切れたらだめ。
3. 報酬Ciはマイナスの場合もある

Point

• 取り去るのではなく、最小全域木になるよう必要な辺を加える
• 報酬小さい順に貪欲に加える
• 報酬がマイナスの辺は最初に全部つなぐ
• 最小全域木は、すでに連結済みかをUnionFindで確認して、連結してない場合のみつなぐことで得られる

UnionFindは以前自分で書いたのを用いたが、TLEしてしまったので一部修正

連結時に集団の大きい方が親になるようすることでAC
こちらを参考にさせて戴きました。

import sys
sys.setrecursionlimit(2000000)

N, M = map(int, input().split())
# 順番を入れ替えて、Cが頭に来る様に読み込み
CBA = [list(map(int, input().split()))[::-1] for _ in range(M)]
# Cの大きさ順にソート
CBA.sort()

# UnionFind
class UnionFind():
    def __init__(self, max_size:int):
        #self.parent = [i for i in range(max_size)]
        self.parent = [-1]*N

    def root(self, id):
        if self.parent[id] < 0:
            return id
        else:
            self.parent[id] = self.root(self.parent[id])
            return self.parent[id]

    def linking(self, id1, id2):
        # 元のままだとTLEになるので、大きな集団が親になる様に修正
        
        id1 = self.root(id1)
        id2 = self.root(id2)
        if id1 == id2:
            return
          
        if self.parent[id1] > self.parent[id2]:
            id1, id2 = id2, id1
        self.parent[id1] += self.parent[id2]
        self.parent[id2] = id1
             
    def chk_link(self, id1, id2):
        if self.root(id1) == self.root(id2):
            return True
        else:
            return False

uf = UnionFind(N)
gain = 0

for c, b, a in CBA:
    #cが負の場合は繋いだ方がお得なので繋ぐ
    if c <= 0:
        uf.linking(b-1, a-1)
        continue
    # すでに連結されているなら繋がずに報酬を得る、繋がってないなら繋ぐ
    if uf.chk_link(b-1, a-1):
        gain += c
    else:
        uf.linking(b-1, a-1)
print(gain)

ABC218-D ~長方形が何個作れるか~

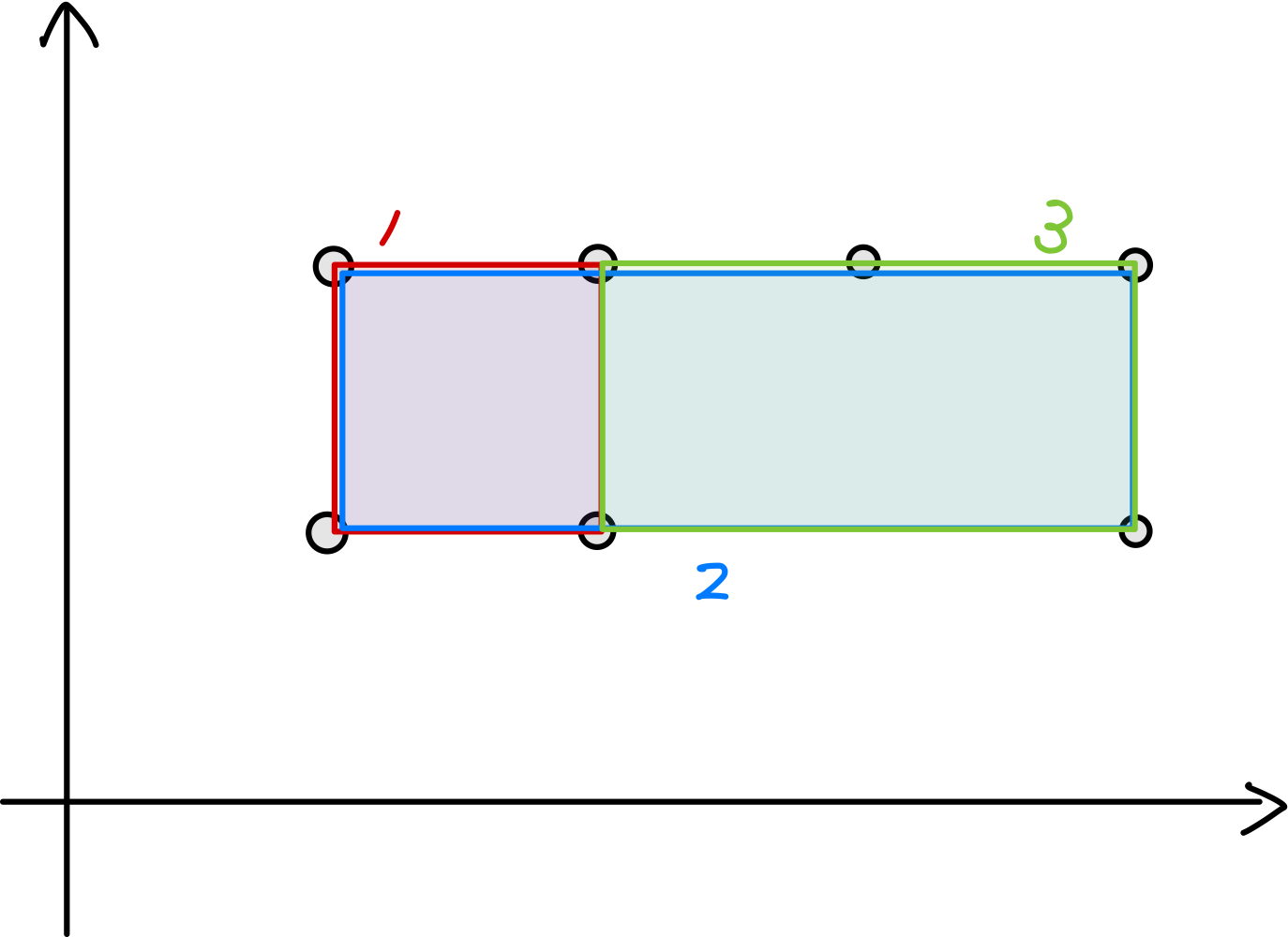
1. 与えられた節点座標を繋いで作れる長方形は何個あるか？
   長方形の各辺はxy軸と平行。下図の場合は3つ作れる

Point

• 各xy座標上にある点のxy座標を辞書型で持っておき、自分の横にある点と上にある点について、総当たりで正方形を作れる点があるかを調べる。
  ①点(xi,yi)について横にいる点（緑枠yj）と上下にいる点（青枠xj）の点の座標を辞書で調べる。
  ②総当たりで、xtoy[xj]にyjが含まれるかを調べる。(点(xj,yj)があるかを調べる)
  ③重複しているので、最後に節点数で割ることに注意

N = int(input())
XY = [list(map(int, input().split())) for _ in range(N)]

# xtoy : x=xi上にある点のy座標リストを返す辞書
# ytox : y=yi上にある点のx座標リストを返す辞書
xtoy, ytox = {}, {}

# 辞書作成
for xi, yi in XY:
    if xi in xtoy:
        xtoy[xi].append(yi)
    else:
        xtoy[xi] = [yi]
    if yi in ytox:
        ytox[yi].append(xi)
    else:
        ytox[yi] = [xi]

cnt = 0
for xi, yi in XY:  #全部の点について順番に考える
    for xj in ytox[yi]: # 自分の横にいる点たちについて総当たり
        if xj == xi: continue #xj=xiは自分自身なのでパス
        for yj in xtoy[xi]: #自分の上にいる点たちについて総当たり
            if yi == yj: continue #yj=yiは自分自身
            if yj in xtoy[xj]: #(xj, yj)の座標があれば長方形が作れる
                    cnt += 1

print(cnt//4) # 重複して数えているので、長方形の節点数4で割る

ABC218-C ~移動と回転で一致 その2~

1. “#”で示された図形が90度ずつ回転と平行移動で一致するかどうか

<形状S>    <形状T>
.....      .....
..#..      ....#
.###.      ...##
.....      ....#

Point

• ABC207-Dを少し改良すれば流用可能。
  　コンテスト中は間違って重心移動を消してしまい、ACできなかった。
  　ちゃんと理解して（復習して思い出して）使い回さないとだめ。
  　戒めのためにここに記録。
• 90度回転だけなので、2次元リストを回転させて調べるのが想定解法と思われる。
  2次元配列のリストは次の式で回転できる（公式解説）。

S = list(zip(*S))

import math

def main(S,T):
  N = len(S)
  
  if len(S) != len(T):   # 数が違えばNo
    print("No")
    return
  
  if len(S) ==  1:
    print("Yes")
    return

  # 重心を原点に移動
  s_mean = sum(S)
  t_mean = sum(T)
  S = [si*N - s_mean for si in S]
  T = [ti*N - t_mean for ti in T]
  
  # sから基準にする点を1点選ぶ。原点だと角度が分からないので、0でない点
  for s_base in S:
    if s_base:
      break

  # s基準がどのTに相当するかは総当たり
  for ii, t_base in enumerate(T):
    if abs(s_base) == abs(t_base): # 重心を0に移動しているので、距離が異なる場合はベースでない
      # 回転角度が90度刻みかどうかのチェック。なくてもACだった
      sr = math.atan2(s_base.imag, s_base.real)
      tr = math.atan2(t_base.imag, t_base.real)
      if (sr - tr) % (math.pi/2) < 0.001:
        # sをt_baseでtをs_baseで回転させる
        s_rot = [si*t_base for si in S]
        t_rot = [ti*s_base for ti in T]
        # 集合にする
        s_set, t_set = set(s_rot), set(t_rot)
        # 差集合の大きさを確認
        if not s_set - t_set:
          print("Yes")
          return

  print("No")
  return

N = int(input())
S = [input() for _ in range(N)]
T = [input() for _ in range(N)]

# 形状を座標情報に変換
s = []
t = []
for i in range(N):
  for j in range(N):
    if S[i][j] == "#":
      s.append(complex(i, j))
    if T[i][j] == "#":
      t.append(complex(i, j))

main(s,t)

ABC217-D ~arrayとbisect~

1. 長さLの棒を左端からxの位置でカットしていく
2. 左端から長さiの位置の切れ端の長さは？

Point

• 挿入はbisect.insort、位置確認はbisect.bisect_left(right)
• 配列は型が決まっているならarrayを使うと高速化できる

コンテスト中はarrayを知らなかったので、[0,L//2+1][L//2, L]で
リストを分割して高速化したが、arrayを用いれば間に合った。

import bisect
import array

L, Q = map(int, input().split())
cxes = [list(map(int, input().split())) for _ in range(Q)]

cutting_list = array.array("i",[0, L])

for c, x in cxes:
    if c == 1:
        bisect.insort(cutting_list, x)
    else:
        i = bisect.bisect_left(cutting_list, x)

        print(cutting_list[i] - cutting_list[i-1])

ABC214-D ~UnionFind~

重み付きの木について、最短経路中での最大の重みを求め、全経路について和をとる

point

• その重み経路を通らないといけない経路数はいくつか？に問題を読み変える
• UnionFindを利用してその経路によって新たにできる組み合わせ数を数え上げる

UnionFindは以前に自分で作成したコード↓をベースとして、力技で組み合わせ計算を追加

import sys
sys.setrecursionlimit(2000000)
input = sys.stdin.readline

N = int(input())
UVW = [list(map(int, input().split())) for _ in range(N-1)]

class UnionFind():
    def __init__(self, max_size:int):
        self.parent = [i for i in range(max_size)]
        self.size = [1] * max_size                     # グループのサイズリスト
        self.comb = 0                                  # 今回の問題用の変数。できる組み合わせ数。本来はClassに入れるべきで無い？               
        
    def root(self, id):
        if self.parent[id] == id:
            return id
        else:
            self.parent[id] = self.root(self.parent[id])
            return self.parent[id]

    def linking(self, id1, id2):
        if self.root(id1) == self.root(id2):
            return
        else:
            # 結合前グループの数を掛け合わせることで、できる組み合わせ数をカウント
            self.comb = self.size[self.root(id1)] * self.size[self.root(id2)]
            self.size[self.root(id1)] += self.size[self.root(id2)]
            self.parent[self.parent[id2]] = self.parent[id1]
            
    def chk_link(self, id1, id2):
        if self.root(id1) == self.root(id2):
            return True
        else:
            return False

uf = UnionFind(N)
wuv = [[w, u-1, v-1] for u,v,w in UVW]
wuv = sorted(wuv)

ans = 0
for w, u, v in wuv:
  uf.linking(u,v)
  ans += w * (uf.comb)
print(ans)

ABC213-E ~01BFS~

移動の最短コストを算出
壁はコスト1で2*2マスを破壊できる

point

• 壁がある場合の移動コスト最小は01BFS
• 2*2マスの壁を壊せるので、壁を壊す場合と壊さない場合で異なるloopを使用する

01BFSの概要は↓が分かりやすい

"""
H, W (行数、列数）
..#..
..#..
### ..
.....
"."が道で"#"が壁
コスト1で壁を2×2マス破壊できる
"""

from collections import deque
import sys
input = sys.stdin.readline
sys.setrecursionlimit(10**8)

# input 普通に読み込んでいいが、#を使うのが気持ち悪いので道を0,壁を1にして読み込み
H, W = map(int, input().split())
S = [[0 if s == "." else 1 for s in input()] for _ in range(H)]

INF = 10 ** 10
dxs = [1,0,-1,0]
dys = [0,1,0,-1]

conf = [[False]*W for _ in range(H)]    # 移動済み confirmed 
costs = [[INF]*W for _ in range(H)]     # 移動コスト
costs[0][0] = 0
queue = deque()                         # 両端から追加するのでdequeを使用
queue.append(0)

while queue:
  cid = queue.popleft()                 # cid : current id
  cx = cid % W                          # IDを行列番号に変換
  cy = cid // W                         # cx,cy : current x,y
  
  if not conf[cy][cx]:                  # 確定済みでないなら実行
    conf[cy][cx] = True
    
    # 道がつながっている場合。1マスずつ移動。queueの最初に追加
    for dx, dy in zip(dxs, dys):
      nx, ny = cx + dx, cy + dy                      # nx,ny = next x,y
      if 0 <= nx and nx < W and 0 <= ny and ny < H:  # 枠内チェック
        if S[ny][nx] == 0:                           # 道がつながっているかチェック
          if costs[ny][nx] > costs[cy][cx]:          # 移動先コストが今より高いなら
            costs[ny][nx] = costs[cy][cx]            # コストを更新して
            queue.appendleft(ny * W + nx)            # queueの最初についか

    # 道がつながっていない場合。2マス先まで移動可能。queueの最後に追加
    for nx in range(cx-2, cx+3):                     # xy2マス先まで2重ループ
      for ny in range(cy-2, cy+3):
        if (abs(nx - cx) + abs(ny - cy) == 4): continue # 斜めに2マス移動はダメ
        if 0 <= nx and nx < W and 0 <= ny and ny < H:
          if costs[ny][nx] > costs[cy][cx] + 1:      # 移動先コストが今＋1より高い場合
            costs[ny][nx] = costs[cy][cx] + 1        # コストを更新して
            queue.append(ny * W + nx)                # queueの最後に追加

# 右下への移動コストを出力
print(costs[H-1][W-1])

# for cost in costs:
#  print(cost)

ABC213-D ~オイラーツアー~

経路を記録しながら深さ優先探索

point

• 訪れた節点情報の書き出しタイミングに注意

import sys
sys.setrecursionlimit(500000)
input = sys.stdin.readline

N = int(input())
roads = [[] for _ in range(N)]
for id in range(N-1):
  A, B = map(int, input().split())
  roads[A-1].append(B-1)
  roads[B-1].append(A-1)
  
route = []
def dfs(id, p=-1):       # 親情報も受け渡す
  route.append(id+1)     # 訪れたタイミングでルートに追加
  queue = sorted(roads[id])
  for nid in queue:
    if nid != p:         # 親は訪問済みなので行かない
      dfs(nid, id)
      route.append(id+1) # 一度戻って新しい設定にいくのでここでも追加

dfs(0)
print(*route)

ABC213-C ~座標圧縮~

数値が存在しない行列を飛ばす

point

• 辞書{古い行列番号：新しい行列番号}を作る
• 重複はややこしいのでset型に一度変換してなくしておく

"""
H, W, N (H行W列N点）
a1 b1 (点1がa1行b1列に存在する）
a2 b2
"""

from sys import stdin
input = stdin.readline

H, W, N = map(int, input().split())
row, col = [], []
for id in range(N):
  a, b = map(int, input().split())
  row.append(a)
  col.append(b)

# 前から順番に新しい番号を振るためソート。重複がややこしいので一度setにする
row_s = list(sorted(set(row)))
col_s = list(sorted(set(col)))
# 最初の行列番号:新しい番号の辞書
dic_r = {ri:id+1 for id, ri in enumerate(row_s)}
dic_c = {ci:id+1 for id, ci in enumerate(col_s)}

# 新しい行列番号に変更して書き出し
for ri, ci in zip(row, col):
  print(dic_r[ri], dic_c[ci])

ABC213-A ~ビット演算~

A xor C = B, A,BからCを求める

• ビット演算で検索すれば色々出てくる
  簡単な例を↓に記載

# input
A = 0b1010
B = 0b1100
print("A = {0:2d} = 0b{0:04b}, B = {1:2d} = 0b{1:04b}".format(A, B))

print("A and B = A & B = {0:2d} = 0b{0:04b}".format(A & B)) 
print("A or  B = A | B = {0:2d} = 0b{0:04b}".format(A | B)) 
print("A xor B = A ^ B = {0:2d} = 0b{0:04b}".format(A ^ B)) 

print("A and C = A -> C = 0b1111 = {0:2d} = 0b{0:04b}".format(0b1111))
print("A & 0b1111 =", A & 0b1111)
print("A xor C = B -> C = A ^ B = {0:2d} = 0b{0:04b}".format(A ^ B))
print("A xor (A xor B) = A ^ A ^ B =", A ^ A ^ B)

A = 10 = 0b1010, B = 12 = 0b1100
A and B = A & B = 8 = 0b1000
A or B = A | B = 14 = 0b1110
A xor B = A ^ B = 6 = 0b0110
A and C = A -> C = 0b1111 = 15 = 0b1111
A & 0b1111 = 10
A xor C = B -> C = A ^ B = 6 = 0b0110
A xor (A xor B) = A ^ A ^ B = 12

ABC212-D ~数列の最小値取出しと足し算~

次の操作を任意の順に任意回実施。

1. 数列に数字を追加
2. 数列の各値にaを加える
3. 最小値を取り出す

point

• 足し算は加えたことにして取り出す前後に操作する
• 数列の順番操作はheapqが早い
  Heapqの基本形はこちらが参考になる

“””
Input例
5
1 2
2 2
3
1 3
3
“””

import heapq

def main():
  Q = int(input())
  h = []
  ad = 0

  for _ in range(Q):
    qi = list(map(int, input().split()))
    if qi[0] == 1:
      heapq.heappush(h, qi[1]-ad)
    elif qi[0] == 2:
      ad += qi[1]
    else:
      print(heapq.heappop(h) + ad)
   
main()

ABC211-D ~BFSで最短経路と経路数dp~

無向グラフで頂点0からNに移動する場合の最短経路とその経路数合計
最短経路はBFS、経路数は深さ順にDP

import sys
sys.setrecursionlimit(1000000)

# 読み込み
N, M = map(int, input().split())
AB = [list(map(int, input().split())) for _ in range(M)]
route = [[] for _ in range(N)]

for a, b in AB:
  route[a-1].append(b-1)
  route[b-1].append(a-1)

# BFS
depth = [-1] * N
depth[0] = 0
queue = [[0,0]]
for myid, pid in queue:
  depth[myid] = depth[pid] + 1
  for nextid in route[myid]:
    if depth[nextid] == -1:
      queue.append([nextid, myid])
      depth[nextid] = 0

mod = 10**9+7
dp = [0]*N
dp[0] = 1

for myid, _ in queue:
  for nextid in route[myid]:
    if depth[nextid] == depth[myid] + 1:
      dp[nextid] += dp[myid] % mod
      
print(dp[-1] % mod)

ABC211-C ~作れる文字列の種類数dp~

任意の文字列から単語を抜き出してtarget文字列を作る
単語の順番入れ替えは不可とした場合に、通り数を数える

S = input()
target = "chokudai"
mod = 10**9 + 7

S = [s for s in S if s in target]
tl = len(target)
sl = len(S)

# dp[tl+1][sl+1] 1枠大きく作って初期値を入れる
dp = [[1]+[0]*tl for _ in range(sl+1)]
  
# dp計算
for sid, s in enumerate(S):
  for tid, t in enumerate(target):
    if s == t:
      dp[sid+1][tid+1] = (dp[sid][tid] + dp[sid][tid+1]) % mod
    else:
      dp[sid+1][tid+1] = (dp[sid][tid+1]) % mod

print(dp[-1][-1])

# ABC210-C ~辞書を利用したカウント~

長さNの数列から長さKの数列を取り出した時に、含まれる数字の種類の最大値

- from collections import defaultdict  
  辞書に未登録のkeyでもErrorにならない
 
  Collectionsはこちらが詳しい

https://qiita.com/apollo_program/items/165fb01b52702274936c

```python

from collections import defaultdict

N, K  = map(int, input().split())
C = list(map(int, input().split()))

col_dict = defaultdict(int)
ans = 0
for id, ci in enumerate(C):
  col_dict[ci] += 1
  if id >= K:
    col_dict[C[id-K]] -= 1
    if col_dict[C[id-K]] == 0:
      del col_dict[C[id-K]]
  ans = max(ans, len(col_dict)) 
               
print(ans)

ABC208-D ~warshall-Floyd法~

一方通行の道。全ての節点候補間移動にかかる最短時間。
通れる接点の制限あり

Point

• warshall-Floyd法で3回ループを繰り返すことで全ての最短経路が求められる
  考え方は↓が参考になる

N, M = map(int, input().split())
paths = [[1000000000] * N for _ in range(N)]
for _ in range(M):
  a,b,c = map(int, input().split())
  paths[a-1][b-1] = c
  
def warshall_floyd():
  total = 0
  for k in range(N):
    for i in range(N):
      for j in range(N):
        if i == j:
          continue
        paths[i][j] = min(paths[i][j], paths[i][k]+paths[k][j])
        if paths[i][j] < 1000000000:
          total += paths[i][j]
  return total

print(warshall_floyd())

ABC207-D ~平行移動と回転移動による一致~

2次元平面上の点群たちが平行移動と回転移動だけで一致させられるか？

point

• 回転は複素数型を使うのが便利
  complex(a, b)

• 基準ペアを1つ決めると移動量が、2点決めると移動と回転を定められる。　　
  重心を調べれば、基準点を決めなくても移動量が分かる

• setは引き算で差集合を求められる。
  もちろん==で一致を調べてもOK

def main():

  N = int(input())
  S = [complex(*map(int, input().split())) for _ in range(N)]
  T = [complex(*map(int, input().split())) for _ in range(N)]

  # N=1ならyesで終了
  if N == 1:
    print("Yes")
    return 0
  
  # 重心を原点に移動
  s_mean = sum(S)
  t_mean = sum(T)
  S = [si*N - s_mean for si in S]
  T = [ti*N - t_mean for ti in T]

  # sから基準にする点を1点選ぶ。原点だと角度が分からないので、0でない点
  for s_base in S:
    if s_base:
      break

  # s基準がどのTに相当するかは総当たり
  for t_base in T:
    if abs(s_base) == abs(t_base):
      # sをt_baseでtをs_baseで回転させる
      s_rot = [si*t_base for si in S]
      t_rot = [ti*s_base for ti in T]
      # 集合にする
      s_set, t_set = set(s_rot), set(t_rot)
            
      # 差集合の大きさを確認
      if not s_set - t_set:
        print("Yes")
        return
  
  print("No")
  return 0

main()