Machines Learning 学习笔记(Week4&5)

##Neural Networks

1. Concept

$a_i^{(j)}$ = "activation" of unit $i$ in layer $j$
$Θ^{(j)}$ = matrix of weights controlling function mapping from layer $j$ to layer $j+1$

2. Model Representation
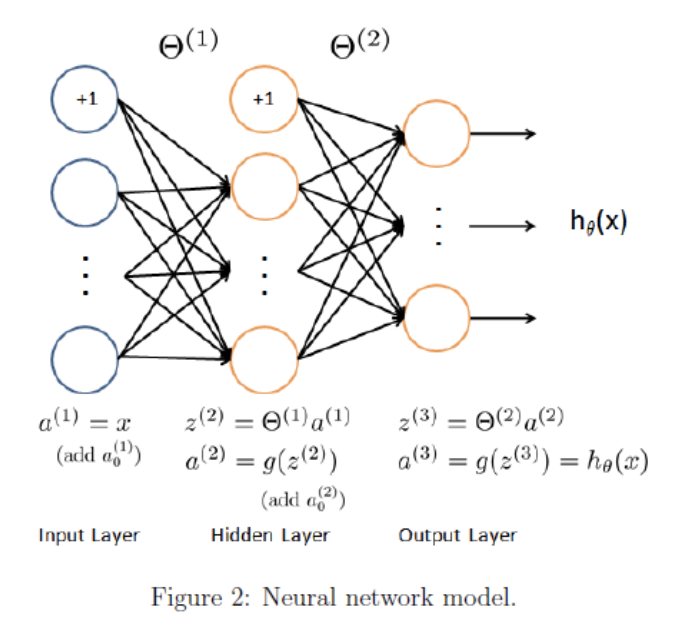
set $x=a^{(1)}$,

$z^{(j)} = Θ^{(j-1)}a^{(j-1)}$
$\searrow$
$a^{(j)} = g(z^{(j)})$
$\swarrow$
$z^{(j+1)}= Θ^{(j)}a^{(j)}$
$\searrow$
$h_Θ(x) = a^{(j+1)} = g(z^{(j+1)})$

3. Application Example

4. Feedforward Propagation Computation Example

5. Cost Function

J(Θ) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K
\Biggl[y_k^{(i)}log\Bigl( \bigl(h_Θ(x^{(i)})\bigr)_k\Bigr)
+ (1-y_k^{(i)})log\Bigl(1- \bigl(h_Θ(x^{(i)})\bigr)_k\Bigr)\Biggr]
+ \frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{S_l} \sum_{j=1}^{S_l+1}
(Θ_{j,i}^{(l)})^2

• $L$ = total number of layers in the network
• $S_l$ = number of units (not counting the bias unit) in layer l
• $K$ = number of output units/classes

• the double sum simply adds up the logistic regression costs calculated for each cell in the output layer
• the triple sum simply adds up the squares of all the individual Θs in the entire network
• the i in the triple sum does NOT refer to training example i

5. Back propagation
For training example t=1 to m:

1. Set $a^{(1)} := x^{(t)}$

2. Perform forward propagation to compute $a^{(l)}$for l=2,3,...,L
   

3. Using $y^{(t)},compute , \delta^{(L)} = a^{(L)} - y^{(t)} $

4. Compute $\delta^{(L-1)}, \delta^{(L-2)},...,\delta^{2} , using , \delta^{(t)} = \bigl( (Θ^{(l)})^T\delta^{(l+1)}\bigr).*a^{(l)}. *(1-a^{(l)})$
   *note: $(a^{(l)}. *(1-a^{(l)}) = g^{'}(z^{(l)}) ,\leftarrow (g-prime)$

5. $ Δ^{(l)} := Δ^{(l)} + a_j^{(l)} \delta_i^{(l+1)}$
   or with verctorization: $ Δ^{(l)} := Δ^{(l)} + \delta^{(l+1)} (a^{(l)})^T$
   Hence we update our new Δ matrix.

• $D_{i,j}^{(l)} := \frac{1}{m} (Δ_{i,j}^{(l)} + \lambda Θ^{(l)}),, if , j \neq 0. $
• $D_{i,j}^{(l)} := \frac{1}{m} Δ_{i,j}^{(l)},, if , j = 0. $

6. Putting It Together: Training a Neural Network

1. Randomly initialize the weights
2. Implement forward propagation to get $h_Θ(x^{(i)}) ,for ,any ,x^{(i)}$
3. Implement the cost function
4. Implement backpropagation to compute partial derivatives
5. Use gradient checking to confirm that your backpropagation works. then disable gradient checking
6. Use gradient descent or a built-in optimization function to minimize the cost function with the weights in theta

When we perform forward and back propagation, we loop on every training example:

for i = 1:m,
   Perform forward propagation and backpropagation using example (x(i),y(i))
   (Get activations a(l) and delta terms d(l) for l = 2,...,L