【SWAT】感度解析と不確実性解析

はじめに

この記事ではSoil and Water Assessment Tool（SWAT），特にSWAT+におけるパラメータの感度解析，不確実性解析について解説します。SWATplusRを使用することを想定してRを用いてコードを実装しました。
ご意見、改善点等あれば是非よろしくお願いいたします。

感度解析

感度解析とは

感度解析とはパラメータがモデルに与える影響を調べるための解析です。
SWATは必要なデータを入力した後に，SWAT内部のパラメータを様々に変更することでモデルによって得られる推定値を実測値へと近づけます（キャリブレーション）。ただ，SWATは多くのパラメータを保有しており，その全てのパラメータを変更しながらモデルのキャリブレーションを行うとなると非常に多くの計算を必要とします。
そのため，感度解析ではSWATのシミュレーションに大きな影響を及ぼすパラメータを特定し，感度が低いと識別されたパラメーターを排除することにより，その後のキャリブレーションで用いるパラメータの数を限定し，そのモデルのシミュレーションにおける重要なプロセスの特定することができます。
以下ではローカル感度解析，グローバル感度解析の2種類の感度解析について紹介します。

ローカル感度解析

ローカル感度解析とは1つのパラメータのみを変更し，その他のパラメータは一定の値に保ったままモデルを複数回実行することで，そのパラメータがモデルに及ぼす影響を特定する方法です。この場合，それぞれのパラメータについて3-5回のモデル実行で十分だそうです。私は普段15回くらい実行しています。

利点：簡単で迅速

欠点：変更するパラメータの感度が他のパラメータの値に依存することが多く，パラメータがどの程度影響するかその精度は不明瞭

実際に動かしてみる

実測値のデータ形式

observed.csvには以下の形式でデータが格納しています。
日付の形式が日本では一般的でない形になっていることに注意して下さい。

date	Flow
29/11/1999	0.21
30/11/1999	0.30
1/12/1999	0.22

出力結果

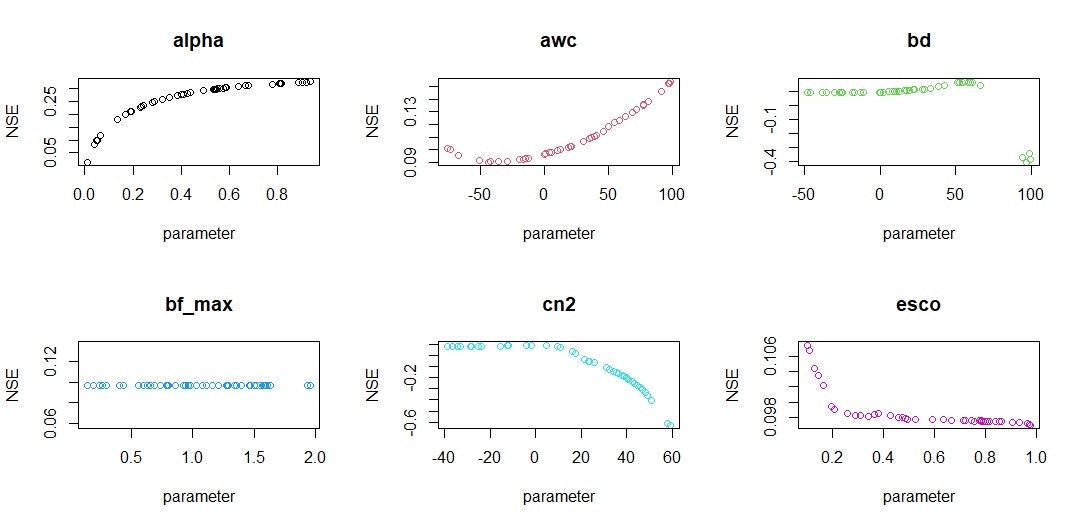
以下のグラフの様な形式でパラメータとナッシュサトクリフ係数（NSE）の関係を表現することができます。

ソースコード

    library(SWATplusR)
    library(tidyverse)
    library(dplyr)
    library(ggplot2)
    library(hydroGOF)

    ModelRun <- function(){
        q_sim <- run_swatplus(project_path = path_plus,
                    output = list(Flow_Sim = define_output(file = "channel_sd",
                                                            variable = "flo_out",
                                                            unit = 5)),
                    parameter = par_set,
                    output_interval = "d",
                    n_thread = 22,
                    start_date  = "1999-11-01",
                    end_date = "2005-10-31",
                    years_skip = 1,
                    revision = 60.5)
        return(q_sim)
    }

    # モデル出力結果のNSEを計算
    Evaluate <- function(x){
        # 実測値データの読み込み
        obs <- read_csv(path_obs_flow)
        names <- c()
        nse <- c()
        # 実測値の日付をdate型に変換(obs$dateはobsのdate列を意味する)
        obs$date = as.Date(strptime(as.character(obs$date), format = '%d/%m/%Y'))
        # 推定値と実測値の存在している期間についてのみ処理，NAの存在する行を削除
        obs_sim_lst = drop_na(inner_join(obs, x$simulation$Flow_Sim, by='date'))
        lst_length <- length(obs_sim_lst)
        for (i in 3:lst_length){
            sim <- obs_sim_lst[i]
            obs <- obs_sim_lst[2]
            name <- paste("run_", i-2, sep = "")
            n <- NSE(sim, obs)
            nse = append(nse,n,after = i)
            names = append(names,name,after = i)
        }
        score <- data.frame(
        Name = names,
        NSE = nse
        )
        score <- mutate(.data = score,x$parameter$value)
        return(score)
    }

    # ローカル感度分析で変更させるパラメータとその範囲を入力
    values = c(c("alpha","aqu","absval",0,1), c("k","sol","pctchg",-50,500))
    # TxtInOutのpath
    path_plus <- "D:/User/TxtInOut"
    # 実測値のpath
    path_obs_flow <- "D:/User/observed.csv"
    # それぞれのパラメータでのモデル実行回数
    times = 15
    # 図示するグラフを設定
    split.screen(c(ceiling(length(values)/5/3),3))

    for(i in 1:(length(values)/5)){
        # valuesのデータを成形
        parameter_name = paste(values[1+5*(i-1)],".",values[2+5*(i-1)]," | change = ",values[3+5*(i-1)],sep = "")
        parameter_min = as.numeric(values[4+5*(i-1)])
        parameter_max = as.numeric(values[5*i])
        par_set <-  data.frame(runif(times, parameter_min, parameter_max))
        names(par_set) <- parameter_name
        # モデルの実行
        q_sim <- ModelRun()
        # パフォーマンス評価
        score <- Evaluate(q_sim)
        # グラフへの貼り付け
        screen(i)
        plot(
            # x軸：パラメータの値
            x = eval(parse(text = paste("score$",values[1+5*(i-1)],sep = ""))),
            # y軸：NSE
            y = score$NSE,
            #色の決定
            col = i,
            #ラベルの変更
            main = values[1+5*(i-1)],
            xlab = "parameter",
            ylab = "NSE"
            )
    }

グローバル感度解析

グローバル感度解析とは全てのパラメータを変化させ，モデルを実行することで，それぞれのパラメータがモデルに及ぼす影響を相対的に評価する方法です。この場合，500-1000回のモデル実行が必要です。
このグローバル感度解析は一度に多くのパラメータを変更させることから，パラメータを多数保有するSWATではこの方法が感度解析に適していると言えます。
代表的なグローバル分析方法には，Morris'Elementaly Effects Screening Method，sobol分析，フーリエ振幅感度検定 (FAST)，および拡張フーリエ振幅感度検定 (EFAST)があります。
それぞれ計算方法は異なり，これら4つの分析を比較した研究の結果では特にMorris法がその他の方法と異なる結果を示していました。

利点：パラメータの感度を互いに比較可能（相対値）

欠点（限界?）：計算量が多く，パラメーターの範囲と実行回数がパラメーターの相対的な感度に影響する。

実際に動かしてみる

NSEに関してFAST法を用いた感度解析を実装しました。
observed.csvはローカル感度分析と同じです。

出力結果

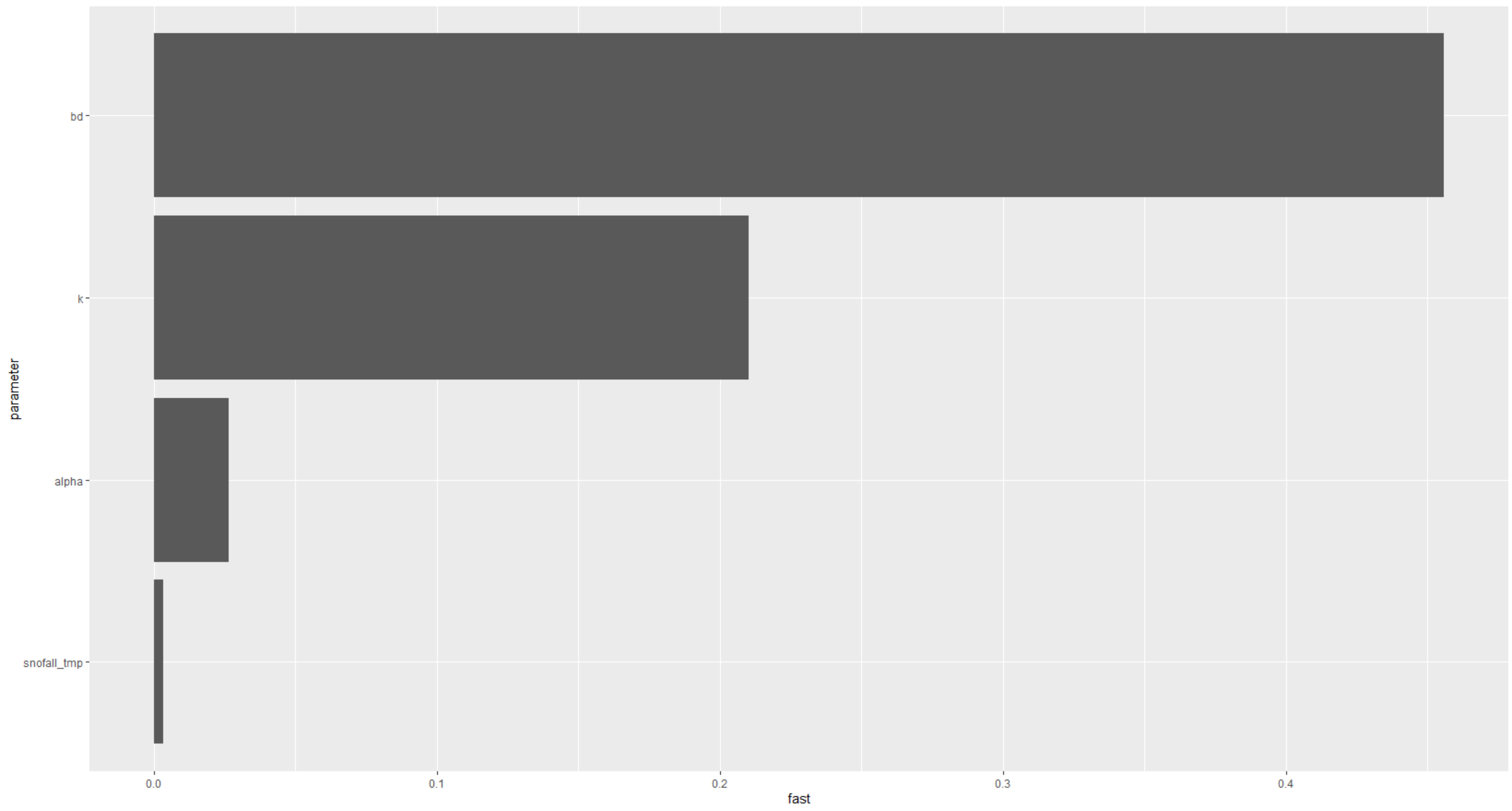
それぞれのパラメータにおける相対的な感度を棒グラフで示しています。値が大きいとそのパラメータがモデルに与える影響が大きいということです。

ソースコード

       library(SWATplusR)
       library(tidyverse)
       library(lubridate)
       library(forcats)
       library(lhs)
       library(fast)
       library(sensitivity)
       library(hydroGOF)
       library(ggplot2)

       # モデル実行
       ModelRun <- function(par_set){
       q_sim <- run_swatplus(project_path = path_plus,
                     output = list(Flow_Sim = define_output(file = "channel_sd",
                                                               variable = "flo_out",
                                                               unit = 5)),
                     parameter = par_set,
                     output_interval = "d",
                     n_thread = 22,
                     start_date  = "1999-11-01",
                     end_date = "2005-10-31",
                     years_skip = 1,
                     revision = 60.5)
       return(q_sim)
       }

       # パラメータの変動作成（Latin Hypercube Sampling）
       MakeFastTable <- function(lst){
              min_lst <- c()
              max_lst <- c()
              name_lst <- c()
              for (i in 1:(length(lst)/5)){
              parameter_min = as.numeric(lst[4+5*(i-1)])
              parameter_max = as.numeric(lst[5*i])
              parameter_name = paste(lst[1+5*(i-1)],".",lst[2+5*(i-1)]," | change = ",values[3+5*(i-1)],sep = "")
              min_lst = append(min_lst, parameter_min, after=i)
              max_lst = append(max_lst, parameter_max, after=i)
              name_lst = append(name_lst, parameter_name, after=i)
              }
              ret <- fast_parameters(minimum = min_lst,
                                          maximum = max_lst,
                                          names = name_lst)
              return(ret)
       }

       # NSE計算
       Evaluate <- function(x){
       # 実測値データの読み込み
       obs <- read_csv(path_obs_flow)
       names <- c()
       nse <- c()
       # 実測値の日付をdate型に変換(obs$dateはobsのdate列を意味する)
       obs$date = as.Date(strptime(as.character(obs$date), format = '%d/%m/%Y'))
       # 推定値と実測値の存在している期間についてのみ処理，NAの存在する行を削除
       obs_sim_lst = drop_na(inner_join(obs, x$simulation$Flow_Sim, by='date'))
       lst_length <- length(obs_sim_lst)
       print(100)
       for (i in 3:lst_length){
              sim <- obs_sim_lst[i]
              obs <- obs_sim_lst[2]
              name <- paste("run_", i-2, sep = "")
              n <- NSE(sim, obs)
              nse = append(nse,n,after = i)
              names = append(names,name,after = i)
       }
       score <- data.frame(
       Name = names,
       NSE = nse
       )
       score <- mutate(.data = score,x$parameter$value)
       return(score)
       }

       # TxtInOutのpath
       path_plus <- "D:/User/TxtInOut"
       # 実測値のpath
       path_obs_flow <- "D:/User/observed.csv
       # ローカル感度分析で変更させるパラメータとその範囲を入力（パラメータは3つ以上設定）
       # シミュレーション実行回数はパラメータ数によって自動で決定
       values = c(c("alpha","aqu","absval",0.1,0.5), c("k","sol","pctchg",-50,50), c("bd","sol","pctchg",0,100), c("snofall_tmp","hru","absval",-5,5))

       # パラメータ作成
       par_fast <- MakeFastTable(values)
       # モデル実行
       q_fast <- ModelRun(par_fast)

       # 実測値読み込み
       q_obs <- read_csv(path_obs_flow,show_col_types = FALSE)
       # NSE計算
       nse_fast <- Evaluate(q_fast)

       # フーリエ変換的な処理
       sens_fast <- sensitivity(nse_fast$NSE, length(values)/5)
       # グラフ整形
       result_fast <- tibble(parameter = q_fast$parameter$definition$par_name,
                            fast = sens_fast) %>%
                            mutate(parameter = factor(parameter) %>% fct_reorder(., fast))
       ggplot(result_fast,
              aes(x = fast, y = parameter)) +
       geom_col()

不確実性解析

不確実性解析とは

不確実性解析とは，モデルの単純化によるプロセスの省略や，点データを広域に適用することによる入力データの誤差などによって発生する出力結果の不確実性を評価する解析です。解析には95%区間(95PPU)，モデル評価のためのp-factor，r-factorを用います( Abbaspour et al., 2004、Abbaspour et al., 2007 )。

95PPU（95 Percent Prediction Uncertainly）

Latin Hypercube Samplingによって決定したパラメータで実行した結果の累積分布における2.5%から97.5%の95%区間(95PPU)です。図はここより拝借。

正規分布における95%信頼区間ではなく，累積分布における95%区間であることに注意。

p-factor

全ての実測値のうち，95PPUバンド内に存在する実測値の割合（0-1）を表しています。実測値の質が高ければ0.8以上，質が低ければ（多くの外れ値が含まれている可能性があれば）0.5以上が望ましい値です。0.7または0.75以上が適切な値だと書いている論文もあります。

r-factor

d-factorと述べている論文もあります。95PPUバンドの厚さの指標。95PPUのバンド厚さの平均を実測値の標準偏差で割ったものとして計算。1.5未満の値が適切です。

実際に動かしてみる

observed.csvはローカル感度分析と同じ。

ソースコードではパラメータを様々に変化させ，モデルの実行結果を95PPUで表すものを作成した。
実際に使用する際は，まず実測値が95PPUの範囲内に収まるように設定し，その後p-factor，r-factorを確認しながらパラメータ変動範囲を狭めていくこととなる（変動幅を狭める方法に関しては実装していません）。

出力結果

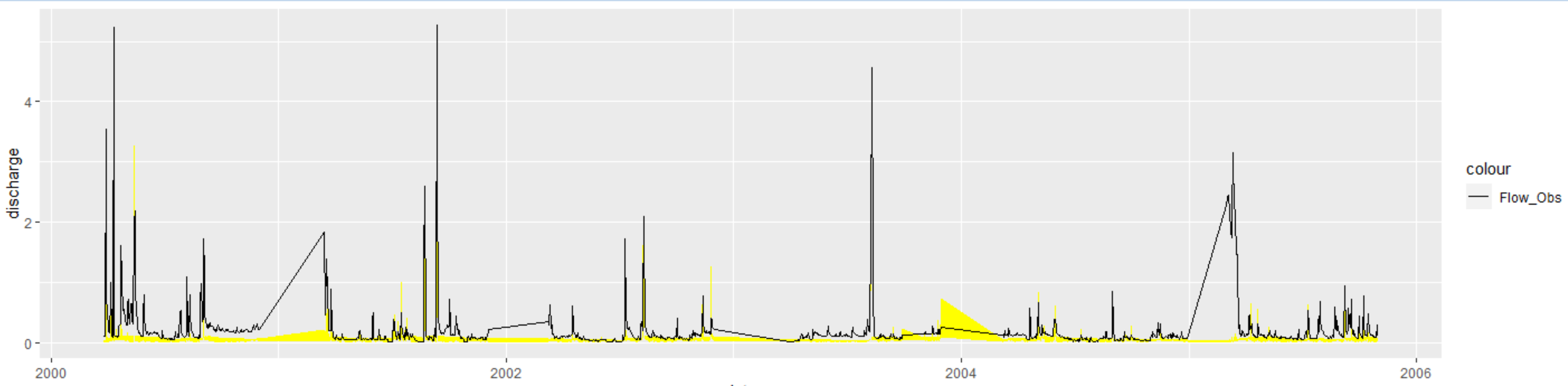
グラフが少し歪ですが，それは期間が跳び跳びなのが原因です。
黄色の帯が95PPU（推定値の変動幅），黒線が実測値です。
このときのp-factorは0.301，r-facorは0.239でした（非常に悪いですね）。

ソースコード

    library(SWATplusR)
    library(tidyverse)
    library(lubridate)
    library(forcats)
    library(lhs)
    library(fast)
    library(sensitivity)
    library(hydroGOF)
    library(ggplot2)
    library(openxlsx)

    # モデル実行
    ModelRun <- function(par_set){
        q_sim <- run_swatplus(project_path = path_plus,
                    output = list(Flow_Sim = define_output(file = "channel_sd",
                                                                variable = "flo_out",
                                                                unit = 5)),
                    parameter = par_set,
                    output_interval = "d",
                    n_thread = 22,
                    start_date  = "1999-11-01",
                    end_date = "2005-10-31",
                    years_skip = 1,
                    revision = 60.5)
        return(q_sim)
    }

    # パラメータの変動作成（Latin Hypercube Sampling）
    MakeFastTable <- function(ary){
        min_vctr <- c()
        max_vctr <- c()
        name_vctr <- c()
        for (i in 1:(length(ary)/5)){
        parameter_min = as.numeric(ary[4+5*(i-1)])
        parameter_max = as.numeric(ary[5*i])
        parameter_name = paste(ary[1+5*(i-1)],".",ary[2+5*(i-1)]," | change = ",values[3+5*(i-1)],sep = "")
        min_vctr = append(min_vctr, parameter_min, after=i)
        max_vctr = append(max_vctr, parameter_max, after=i)
        name_vctr = append(name_vctr, parameter_name, after=i)
        }
        ret <- fast_parameters(minimum = min_vctr,
                                    maximum = max_vctr,
                                    names = name_vctr)
        return(ret)
    }

    # 出力流量データの転置(日付が列名)
    transpose_tbl <- function(df) {
        df_ = select(df,  -date)
        # 転置したtibble作成
        t_df <- data.table::transpose(df_)
        #列名を日付に
        colnames(t_df) <- df$date
        # 一旦データフレーム経由
        t_df <- t_df %>%
        # 列名を表に入れる
        tibble::rownames_to_column(.data = .) %>%
        tibble::as_tibble(.) %>%
        select(-rowname)
        return(t_df)
    }

    # 95PPUの計算
    Calculate95PPU <- function(vctr){
        length_vector = length(vctr)
        # 昇順にソート
        vctr = sort(vctr)
        # 2.5%がリストの何番目なのか（負の値を取らないためにモデル実行回数は40以上が望ましい）
        L_95PPU_num = length_vector * 0.025
        L_95PPU_floor = floor(L_95PPU_num)
        L_95PPU_ceiling = ceiling(L_95PPU_num)
        # 97.5%がリストの何番目なのか
        U_95PPU_num = length_vector * 0.975
        U_95PPU_floor = floor(U_95PPU_num)
        U_95PPU_ceiling = ceiling(U_95PPU_num)

        # indexエラーを避ける（モデル実行回数が40以上なら問題ない）
        if (L_95PPU_floor < 1){
            L_95PPU_floor = 1
        }
        if(U_95PPU_ceiling > length_vector - 1){
            U_95PPU_ceiling = length_vector
        }
        
        # 2.5%の値および, 97.5%の値取得(線形を仮定)，内分点の公式
        # 分母0の処理をelseに示す
        if ((L_95PPU_ceiling - L_95PPU_floor)>0){
            L_95PPU = (vctr[L_95PPU_floor]*(L_95PPU_ceiling - L_95PPU_num) + vctr[L_95PPU_ceiling]*(L_95PPU_num - L_95PPU_floor))/((L_95PPU_ceiling - L_95PPU_floor))
        } else {
            L_95PPU = vctr[L_95PPU_floor]
        }
        if ((U_95PPU_ceiling - U_95PPU_floor)>0){
            U_95PPU = (vctr[U_95PPU_floor]*(U_95PPU_ceiling - U_95PPU_num) + vctr[U_95PPU_ceiling]*(U_95PPU_num - U_95PPU_floor))/((U_95PPU_ceiling - U_95PPU_floor))
        } else {
            U_95PPU = vctr[U_95PPU_floor]
        }    

        #引き算(d求めるのに使用)
        band = U_95PPU - L_95PPU

        return(list("L_95PPU"=L_95PPU, "U_95PPU"=U_95PPU, "band"=band))
    }

    # 95PPUを実測値データと結合
    CombineToObs <- function(path_obs_flow, PPU_tbl){
        obs <- read_csv(path_obs_flow)
        # 実測値の日付をdate型に変換(obs$dateはobsのdate列を意味する)
        obs$date = as.Date(strptime(as.character(obs$date), format = '%d/%m/%Y'))
        # 推定値と実測値の存在している期間についてのみ処理，NAの存在する行を削除
        obs_sim_tbl = drop_na(inner_join(obs, PPU_tbl, by='date'))
        return(obs_sim_tbl)
    }

    # TxtInOutのpath
    path_plus <- "D:/User/TxtInOut"
    # 実測値のpath
    path_obs_flow <- "D:/User/observed.csv"
    # シミュレーション実行回数はパラメータ数によって自動で決定
    values = c(c("alpha","aqu","absval",0.1,0.5), c("k","sol","pctchg",-50,50), c("bd","sol","pctchg",0,100), c("snofall_tmp","hru","absval",-5,5), c("snomelt_min","hru","absval",0,10))

    # パラメータ作成（Latin Hypercube Sampling）
    par_fast <- MakeFastTable(values)
    # モデル実行
    q_sim <- ModelRun(par_fast)
    # 転置
    flow_sim_tbl = transpose_tbl(q_sim$simulation$Flow_Sim)

    # 95PPUのリスト作成
    L_95PPU_vctr = c()
    U_95PPU_vctr = c()
    band_vctr = c()
    # 日付のリスト作成
    date_vctr = as.Date(names(flow_sim_tbl))


    for (i in 1:length(flow_sim_tbl)){
        # 1列毎に抽出，ベクトルに変換
        flow_vctr = as.vector(t(flow_sim_tbl[i]))
        # 95PPU計算
        rets = Calculate95PPU(flow_vctr)

        L_95PPU = rets$L_95PPU
        U_95PPU = rets$U_95PPU
        band = rets$band
        L_95PPU_vctr = append(L_95PPU_vctr, L_95PPU)
        U_95PPU_vctr = append(U_95PPU_vctr, U_95PPU)
        band_vctr = append(band_vctr, band)
    }

    # 95PPUのtibble作成
    PPU_tbl = tibble("date" = date_vctr,
                    "L_95PPU" = L_95PPU_vctr,
                    "U_95PPU" = U_95PPU_vctr,
                    "band" = band_vctr)

    # 実測値と結合（NAを含む列を削除）
    combinedTbl = CombineToObs(path_obs_flow, PPU_tbl)

    # p-factorの計算
    count_in = 0
    count_all = 0
    for (i in 1: length(combinedTbl$Flow)){
        if((combinedTbl$U_95PPU[i] >= combinedTbl$Flow[i]) && (combinedTbl$Flow[i] > combinedTbl$L_95PPU[i])){
            count_in = count_in + 1
        }
        count_all = count_all + 1
    }
    p_factor = count_in/count_all

    # r-factorの計算
    r_factor = mean(combinedTbl$band)/sd(combinedTbl$Flow)

    # 結果出力
    print(paste("p-factor: ",p_factor,",r-factor: ",r_factor, sep = ""))

    # グラフ作成
    graph = ggplot(data = combinedTbl, aes(date)) +
            geom_ribbon(aes(ymin = L_95PPU, ymax = U_95PPU), 
                            fill = "yellow") +
            geom_line(aes(y = Flow, colour = "Flow_Obs")) +
            scale_color_manual(values = c("1e1e1e")) +
            ylab("discharge")

    print(graph)

おわりに

コードは適宜変更していいかんじに使ってください。

参考文献