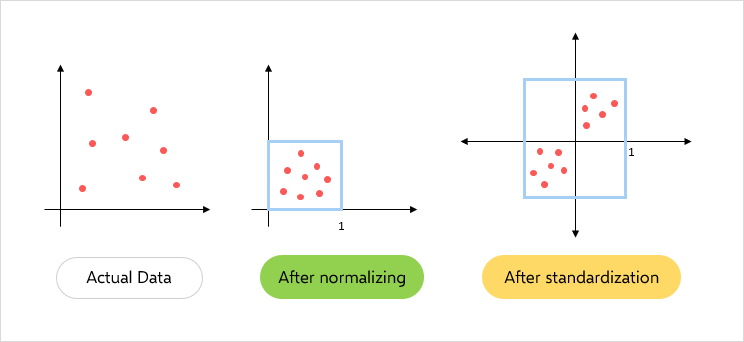
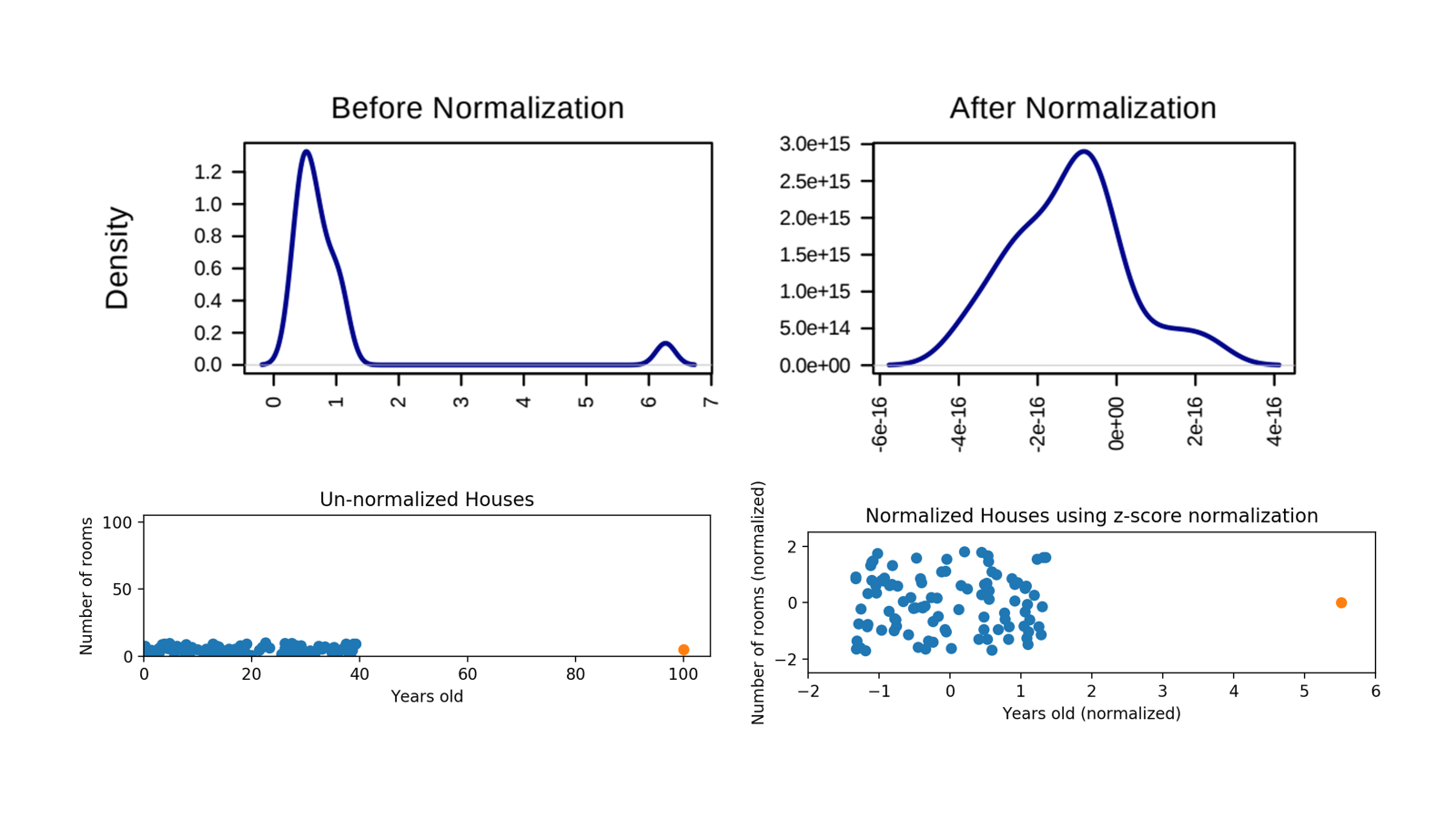
最近悩んでいることの一つであるデータ処理・補正...
実験データって、そのまま使えることは少ないですよね?
「何のデータか」にもよりますが、多くの場合、補正や処理を行った後に、可視化や解析を行います。
補正する方法って、例えば、内部標準物質で補正したり、中央値をそろえたり、スケーリングしたり(また何種類かもあるし)、総量で補正したり、log使ったり、QCで補正したりなど...
え~無理 ![]() どんだけやればいいの? 何がゴールなの??
どんだけやればいいの? 何がゴールなの??
という質問に、今回の記事で答えられたらと思います!
(ps.「質量分析のデータを扱う上で」という前提の文章が多いかもしれません)
そもそもなんで補正するん?
実験を行う上で、データが1つしかない場合は、結果が良くても悪くても「本当なの?」と確信できないということが多いので、少なくとも 複数のレプリケート(繰り返しデータ) を取得します。レプリケートが多くなればなるほどサンプル間の差が生じやすく、その差を補正するため、つまり、手技的な差やデータの偏りを補うためにやるものが「補正」。
例えば:
・同じサンプルでも測定条件の微妙なズレや機器の感度差で数値が異なる。
・細胞数が異なると、サンプル間の絶対値に差が出る。
・バッチ間で測定日の違いが誤差を生む。
これらの偏りや誤差を補正して、データの「信頼性」を高めます。
どうやって選ぶの?
選ぶには、自分がどのようなデータを用いていて、どこで誤差が出やすいかというのが大きく関係します。簡単に言えば、目的に応じて。。。
例えば、細胞のデータならサンプル間の細胞数が多少異なるため、目的に応じて細胞数や含まれるタンパク質か脂質の量で補正したり、内部標準物質の強度か面積で補正したり、解析時のバッチ補正にQCを使ったりすると思います。
補正方法は「どのデータを使っているか」「どこで誤差が出やすいか」によって異なります。
例えば:
目的: サンプルごとの総量差を補う。
方法: 脂質のデータなら、各サンプルの総脂質量で補正。
目的: 機器や手技の影響を補正。
方法: 測定時に添加した内部標準物質の強度を基準に補正。
目的: 測定値のばらつきをそろえる。
方法: 各サンプルの値を中央値で正規化する。
目的: 異なるスケールのデータを比較可能にする。
方法: zスコア(平均0、標準偏差1)やlog変換。
目的: バッチ間や経時変化の補正。
方法: 質量分析データでQCサンプルを使い、補正曲線を作成。
でもでも、分かっていて、分かっているものでやっても 「これでいいの?」 というのが出てこないです?![]()
どこが目標なの?何が補正できているのかの基準?
一番大事な部分の気がします!!というか今までずっと悩んでいた部分、、
ある程度見るものが決まっていて、そのための手技で実験していれば、特に必要がないと思いますが、それ以外の場合、つまり、色々みたい!というときにはデータをどう補正するかによって見え方がめちゃくちゃ変わるー!
なんでかというと、
データって多くなればなるほど分散するより、偏ってしまうケースも多いし、ものによって比較しづらかったりします。例えば、二種類のものをそのまま比較しようとすれば、スケールが異なるかも、そもそもめちゃくちゃあるものがめちゃくちゃ変化しているのに、それが少しだけあって、少しだけ変化していないものと同じく見えちゃうかもということです。
なので、データの偏りを補正するという意味で、データができるだけ分散するようにスケーリングなどで補正します。
具体例: データの偏りの補正
例えば、以下の2つの成分を比較するとします:
| 成分 | 量の変化 | 測定結果 |
|---|---|---|
| 成分A(多い) | 大きく変化 | 100 → 150 |
| 成分B(少ない) | 小さく変化 | 5 → 6 |
補正前のデータだと、成分Aの変化が圧倒的に目立ちます。
しかし、データのスケールが異なるため、成分Bの変化も重要な意味を持つかもしれません。
補正方法:スケーリング
データをスケーリング(例: zスコアやlog変換)すると、成分Bの変化も適切に反映され、比較がしやすくなります。
データ補正のまとめ:正確で効率的な解析のために
データの補正は、手技や測定の誤差を最小限に抑え、正しく比較・解析するために行います。
目的に応じた補正手法を選ぶ(総量、内部標準、QC補正など)。
データの偏りやばらつきを適切に補正することで、「正しい解釈」 と 「効率的な解析」 が可能になると思います。
豆知識になればうれしいです!
** Holly, jolly, merry christmas! And wish you all the best in 2025! <3 **