Python でグラデーション中の色を求める

たとえ車輪の再発明だとしても¹、私は Python でグラデーションの色を得る関数を書きたいと思った。

実装

以下に実装を示す。

import colorsys
import math

def gradation(position, *, start, stop):
    start_hls = colorsys.rgb_to_hls(*start)
    stop_hls = colorsys.rgb_to_hls(*stop)

    delta = [j - i for (i,j,) in zip(start_hls, stop_hls)]
    delta[0] = (delta[0] + 0.5) - math.floor(delta[0] + 0.5) - 0.5

    hls = [i + position * j for (i,j,) in zip(start_hls, delta)]
    return colorsys.hls_to_rgb(*hls)

Numpy を利用する場合

import colorsys
import math

import numpy as np

def gradation(position, *, start, stop):
    start_hls = np.array(colorsys.rgb_to_hls(*start))
    stop_hls = np.array(colorsys.rgb_to_hls(*stop))
    
    delta = stop_hls - start_hls
    delta[0] = (delta[0] + 0.5) - math.floor(delta[0] + 0.5) - 0.5
    
    hls = start_hls + position * delta
    return colorsys.hls_to_rgb(*hls)

startは開始色、stopは終了色であり、どちらも $[0, 1]$ の領域で示される RGB のタプルである。

positionは $[0, 1]$ の範囲の浮動小数点数で、position=0.のとき返却値はstartに等しく、position=1.のとき返却値はstopに等しい。

一見して意図を理解しづらい部分はdelta[0] = (delta[0] + 0.5) - math.floor(delta[0] + 0.5) - 0.5の部分だろう。

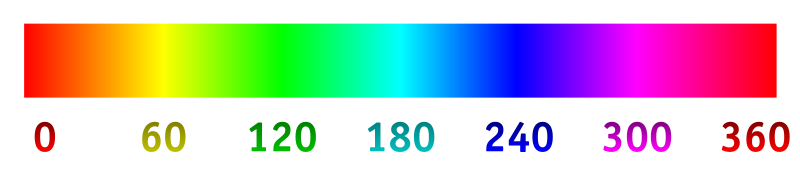
前提として、この関数では色情報を一度 RGB 色空間から HLS 色空間に変換している(この理由については後述する)。 ここで、色相(H)は、$[0, 1)$ の領域で示されているが、実際には 0 と 1 が重なる循環した数構造である。 これゆえに色相環と呼ぶ。

これがある問題を引き起こす。 すなわち、一般の数のように直線状に色相を配置したとき、ピンクと黄色は大きく離れた色のように見える。

しかし、実態に近い円環状に配置された図では、この 2 色は極めて近いことがわかる。

つまり、2 色の色相の差を単純にとったとき、その絶対値が 0.5 を超えているならば、それは「遠回り」をした結果なのである。 0.5 を超えたとき、より短い経路を取る必要がある。 右回りに 0.8 した色は左回りに 0.2 した色に同じなのだから、0.8 を渡して -0.2 が返却される函数が好ましい。 しかし、0.3 に対してはそのまま 0.3 を返却してほしい。

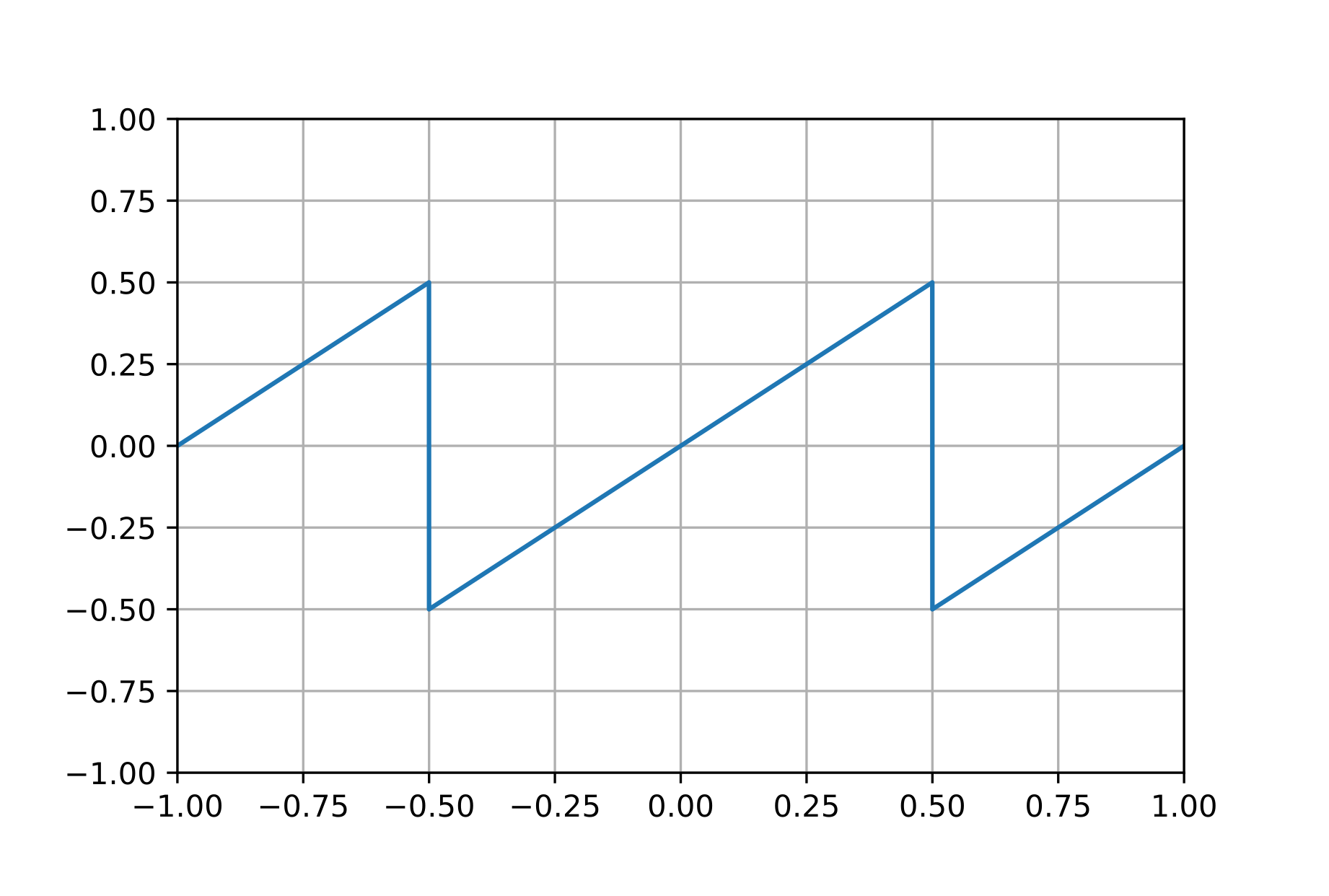
先程挙げた $y = (x + 0.5) - \lfloor x + 0.5 \rfloor - 0.5$ は、その式の見た目からはあまり想像しづらいが、以下のようなのこぎり波を示す。 これは今回の目的にちょうどフィットしているというわけだ。

使った例

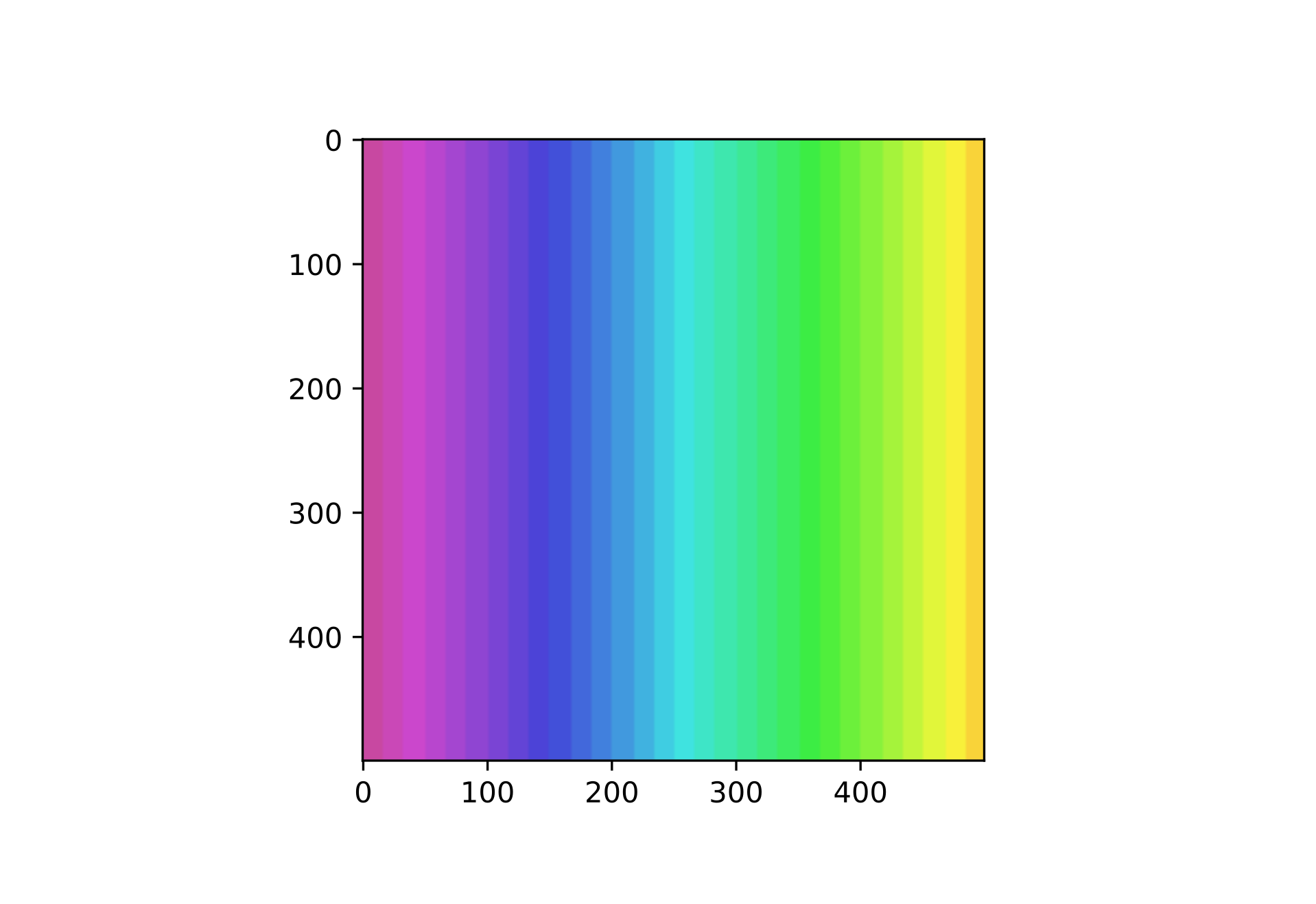
こんな感じで使える。

# import cv2
# import numpy as np
# import matplotlib.pyplot as plt

start = (0.788,0.286,0.635,)
stop = (0.980,0.831,0.227,)
img = np.zeros((500,500,3))
grad_num = 30
shift = 4
for i in range(grad_num):
    color = gradation(i / (grad_num - 1), start=start, stop=stop) # ここ
    width = img.shape[0] / grad_num
    pt1 = (width * i, 0)
    pt2 = (width * (i + 1), img.shape[1])
    pt1 = tuple(np.rint(np.array(pt1) * 2 ** shift).astype(int))
    pt2 = tuple(np.rint(np.array(pt2) * 2 ** shift).astype(int))
    cv2.rectangle(img, pt1, pt2, color=color, thickness=-1, lineType=cv2.LINE_AA, shift=shift)
plt.imshow(img)
plt.show()

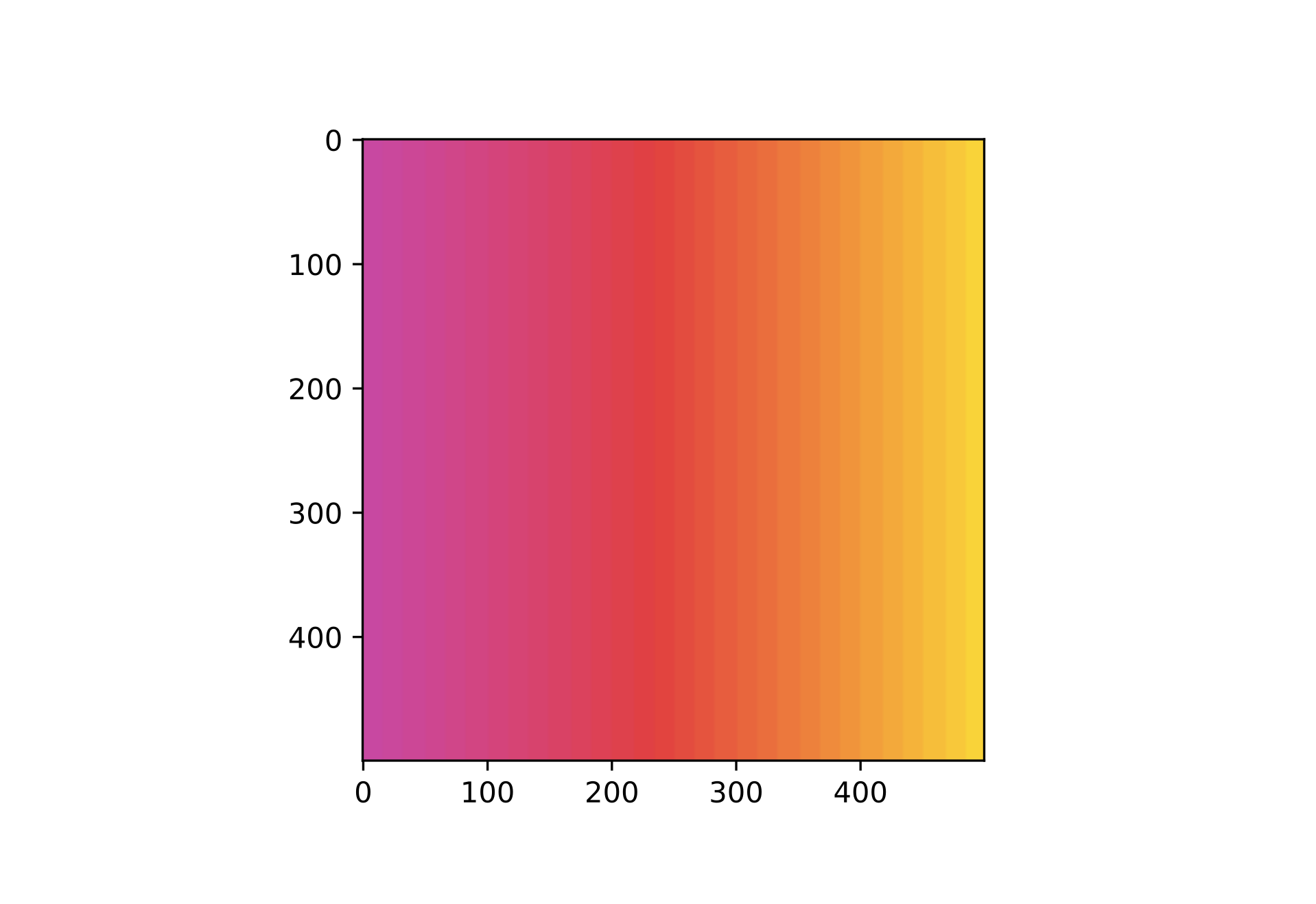
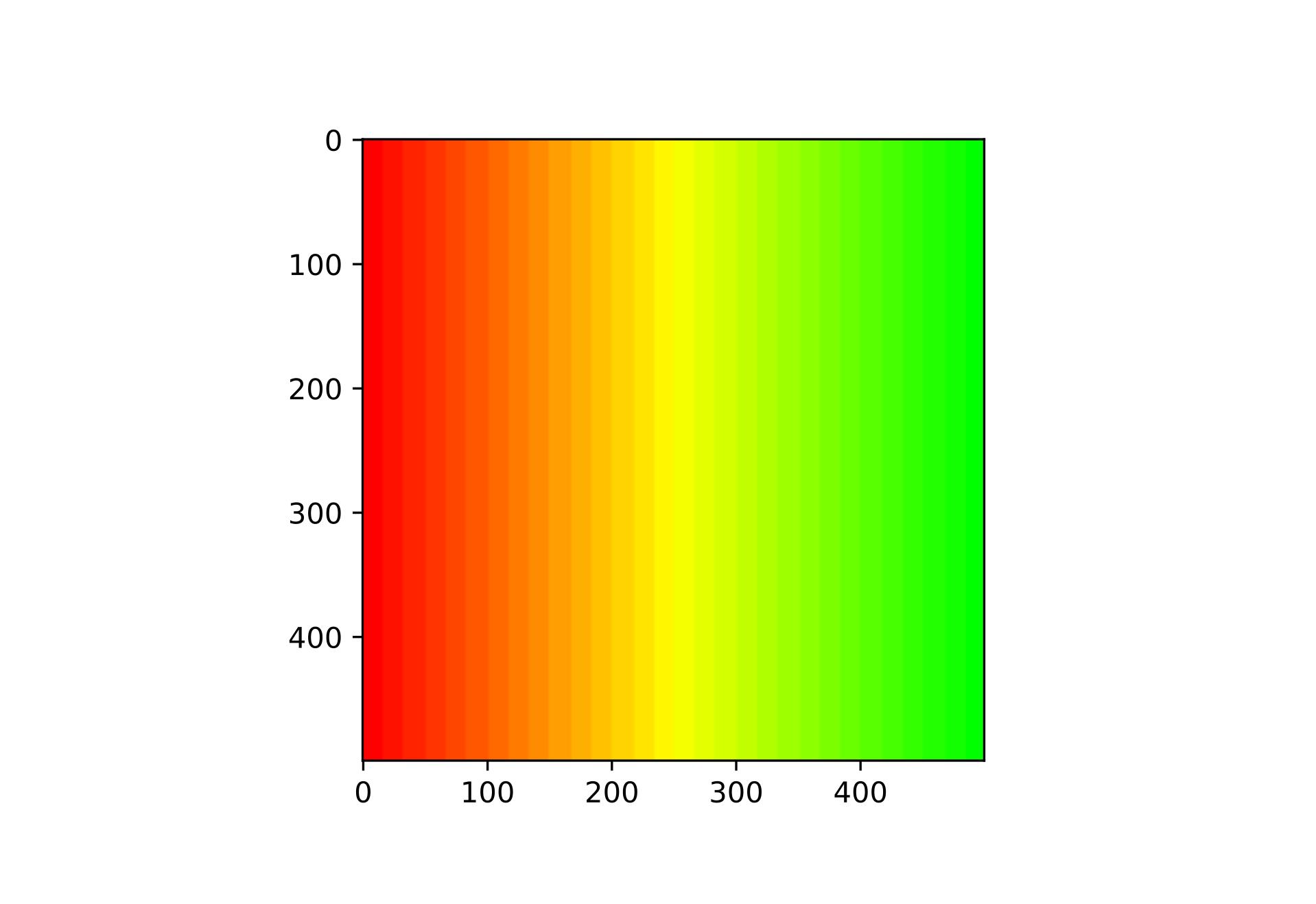
さきほどののこぎり波の部分をコメントアウトするとこうなる。

これはこれできれいだが、ピックした 2 色によって遠回りしたりしなかったり安定しないので、いずれにせよ使い物にはならない。

余談: なぜ HLS なのか

知っている人にはそもそも「なぜ HSV ではなく HLS なのか」と言われそうだが、これに関しては私の好みとしか言いようがない。 もちろん HSV でもいいと思う。

さて、本題の「なぜ RGB ではなく HLS なのか」に関して説明する。

RGB とは赤、緑、青のそれぞれの光の成分の強さによって色を表現する空間である。 この空間でグラデーションをすると困ったことが起こる。 光の成分が違いすぎる二色を選んだとき、途中で光が弱くなりすぎるのだ。

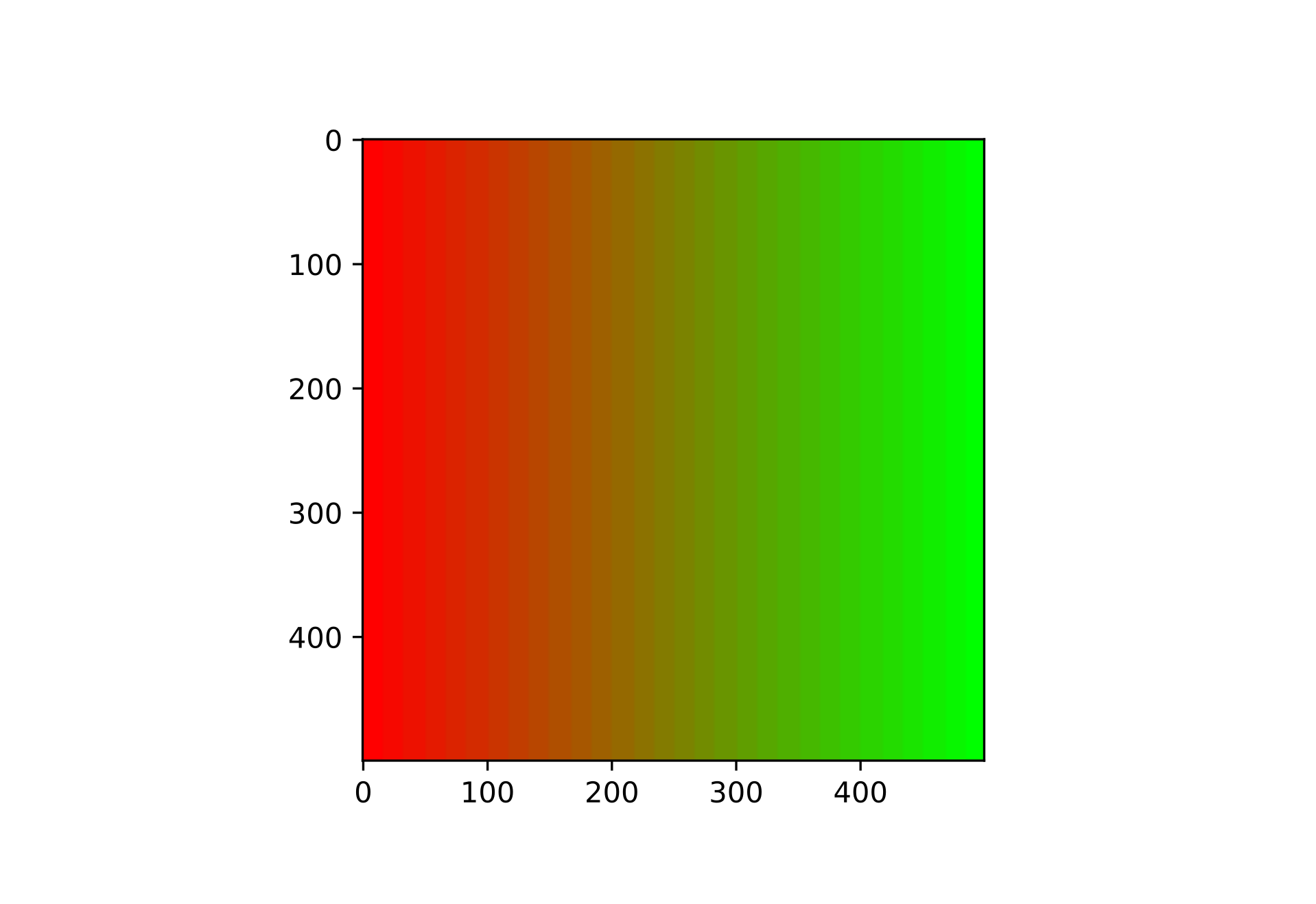
実例を見てみよう。 下は純色の赤から純色の緑までを RGB 色空間で移動させた図である。

赤は当然、赤の成分がマックスで他の光はない。 緑は緑の成分がマックスで他の光がない。 その結果、中間点では赤の弱々しい光と緑の弱々しい光によって非常にくすんだ色合いになってしまうのだ。

HLS(や HSV)色空間では、「どんな色か」「明るいか暗いか」「鮮やかかくすんでいるか」によって色を表現する。 そのため、このような場合でも「どんな色か」の部分のみが変わるのみで、鮮やかなまま色の移動が行えるというわけだ。

1. 実際のところ私の目的を達するよく利用されるライブラリがあるかどうかは知らない。 でも別にいいじゃん ↩