Abstract
この記事は, 数値計算 Advent Calendar 2018 の13日目のコンテンツです. 航空力学や破壊力学などに現われる Carleman 型特異積分方程式の数値解を構成する手順を紹介します.
Introduction
区間 $-1 < x < +1$ において, $\lambda$ を既知定数, $a, f$ を既知の関数とし, Carleman 型特異積分方程式
$$
a(x) u(x) - \lambda \int_{-1}^{+1} \frac{u(\xi)}{\xi - x} \frac{d\xi}{\pi} = f(x)
$$
を考えます. ここで, 積分は Cauchy の主値
$$
\int_{-1}^{+1} \frac{u(\xi)}{\xi - x} \frac{d\xi}{\pi} = \lim_{\epsilon \to 0}
\left(
\int_{-1}^{x-\epsilon}
- \int_{x+\epsilon}^{+1}
\right)
\frac{u(\xi)}{\xi - x} \frac{d\xi}{\pi}
$$
の意味で定義され, これを (Cauchy 型の, あるいは Cauchy 型積分核を持つ) 特異積分と呼ぶことにします. また, この積分変換は有限 Hilbert 変換とも呼ばれます.
この積分方程式は2次元の連続体力学において重要です. 中でも単純な $a \equiv 0$ の場合は, 航空力学において翼の上下の圧力差と揚力とのバランスを表わし, Airfoil 方程式1と呼ばれます. また線形弾性破壊力学では, 2次元弾性体中の直線亀裂に沿う開口あるいは滑りに伴なう亀裂面上の応力変化が摩擦力などと釣り合う様子を記述します. これらの対応について以下の表に纏めます. 航空力学については私の専門外なので, 左辺第一項の物理的意味がわかりませんでしたがご容赦ください.
| 数学的表現 | 航空力学 | 破壊力学 |
|---|---|---|
| 積分区間 $-1 < x < +1$ | 翼が占める領域 | 亀裂が占める領域 |
| 未知関数 $u$ | 翼に沿う渦度分布 | 亀裂両側の変位差(=開口or滑り)分布の微分 |
| 特異積分 $\lambda \int \frac{u(\xi)}{\xi - x} \frac{d\xi}{\pi}$ | 翼の上下の圧力差 | 開口or滑りによる亀裂面上の応力変化 |
| 非斉次項 $f$ | 翼に生じる揚力 | 亀裂面に作用する力(摩擦など)の, 亀裂が生じる前後での差 |
| 関数 $a$ | ? | 摩擦係数の空間分布に比例, ただし亀裂両側の物性が等しい場合はゼロ |
| 左辺第一項$a(x) u(x)$ | ? | $a \ne 0$ のときは, 滑りに伴う摩擦力変化 |
また, 破壊力学における Airfoil 方程式の導出については後の Appendix 1 をご覧ください.
さて, あらかじめ注意しておくべきことは, 有限 Hilbert 変換が
$$
\int_{-1}^{+1} \frac{1}{(\xi - x) \sqrt{1 - \xi^2}} \frac{d\xi}{\pi} = 0
$$
という性質を持つことです(証明は $\xi = \cos{\theta}$, $t = \tan{\frac{\theta}{2}}$ という2段階の置換積分による…のですが, より簡単な方法があれば教えて下さい). この性質により, 特に $a \equiv 0$ の場合にはいかなる解 $u$ についても任意定数 $C$ を用いて
$$
u + \frac{C}{\sqrt{1 - x^2}}
$$
もまた解になってしまい, 従って $C$ を決めるための境界条件が別途必要です. 後に出てくるように, $a \ne 0$ の場合にも類似の性質があり, やはり境界条件を要します.
1. Airfoil 方程式の場合
まずは未知関数 $u$ についての簡単な Airfoil 方程式からいきましょう. ただし上表および Appendix 1 にあるように, 破壊力学では亀裂での変位不連続分布の微分について成り立つ式なので, $u$ の代わりに $u'$ を用いて
$$
\int_{-1}^{+1} \frac{u'(\xi)}{\xi - x} \frac{d\xi}{\pi} = f(x) \quad (-1 < x < +1)
$$
が成り立っているものとします. なおここでは $- \lambda = 1$ としました. この方程式の解は, 有限 Hilbert 変換の反転公式
$$
u'(x) = \displaystyle \int_{-1}^{+1} \sqrt{\frac{1-\xi^2}{1-x^2}} \frac{f(\xi)}{(\xi - x)} \frac{d\xi}{\pi} + \frac{C}{\sqrt{1-x^2}}
$$
により得られます2. この解を数値的に構成する方法の一つは, この積分を数値的に直接評価することです. ただしこれを実践するには, 被積分関数が端点近傍で特異性を持つことに注意する必要があります. Simpson 公式のような単純な数値積分では, この特異性を十分な精度で評価できないことが問題です3. そこで端点に特異性を有する被積分関数を高精度に取り扱い可能な二重指数関数型数値積分公式 (Double Exponential formula=DE 法) を利用するという解決策があります4.
一方, この解の公式を利用せず, 元の特異積分方程式を直接離散化して線形方程式ソルバに渡す境界積分方程式法(Boundary Integral Equation Method=BIEM)という方法もあり, 今回はこれを採用したいと思います. 一般に積分方程式
$$
\int K(x, \xi) u'(\xi) d\xi = f(x)
$$
を数値的に解くための最も簡単な方法は, 積分区間を幅 $\Delta$ ずつ等間隔に $N$ 分割 (つまり $\Delta = 2 / N$, ただし 2 は今回の積分区間の長さ ) し, 近似的に
$$
\sum_{j = 1}^n K\left(x_i, \xi_j\right) u'\left(\xi_j\right) \Delta = f\left(x_i\right)
$$
が成立するとしてベクトル $u'\left(\xi_j\right)$ を求めることですが, 今回は明らかに $K\left( x_i, x_j \right) = \infty$ $(i = j)$ という問題があるので, $x$ と $\xi$ についての評価点をずらす必要があります. このとき, 下図(図1とします)
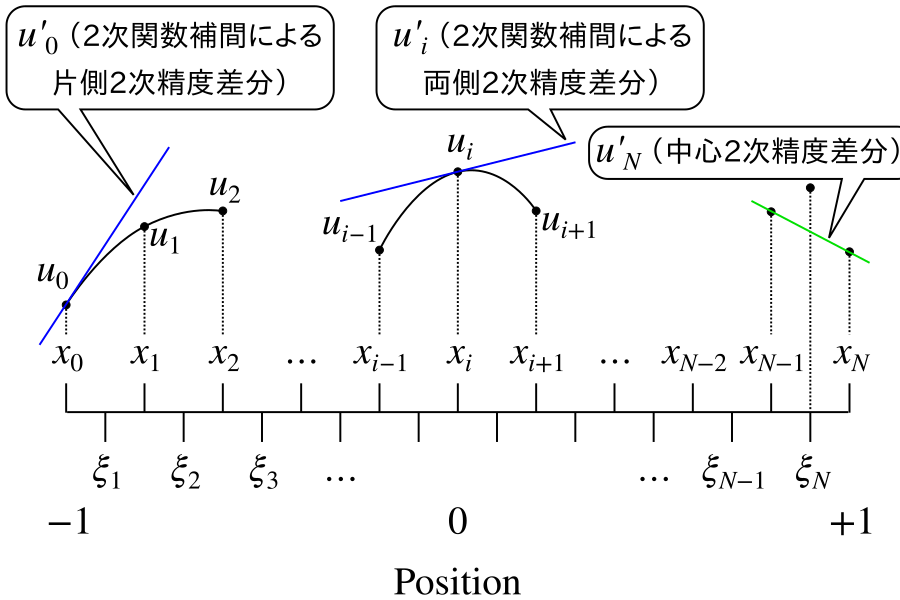
のように分割を対称にしようとすると
\begin{align}
\begin{cases}
x_i = -1 + \frac{2 i}{N}, \, (i = 0, 1, ..., N) \\
\xi_i = \frac{x_{i-1} + x_{i}}{2}, \, (i = 1, 2, ..., N )
\end{cases}
\end{align}
という具合に行列 $K$ が矩形になってしまい, 過剰決定問題となってしまいます. しかしここでは図中右側にある $u'_N$ (緑色直線) のように $u'(\xi_j)$ を中心差分で評価すると,
\begin{align}
\sum_{j=1}^{N} K\left(x_i, \xi_j\right) u'\left(\xi_j\right) \Delta
= & \sum_{j=1}^{N} K\left(x_i, \xi_j\right) \frac{u\left(x_j\right) - u\left(x_{j-1}\right)}{\Delta} \Delta \\
= & - K\left(x_i, \xi_1 \right) u\left(x_0\right) + \sum_{j=1}^{N-1} \left[ K\left(x_i, \xi_j\right) - K\left(x_i, \xi_{j+1}\right) \right] u\left(x_j\right) + K\left(x_i, \xi_N\right) u\left(x_N\right)
\end{align}
が得られ, 評価点 $x_i$ の上でベクトル $f(x_i)$ が与えられた時, 同じ評価点の上でベクトル $u(x_i)$ を求める問題に帰着できました. 後はこれを解くだけですが, 先述の任意定数 $C$ を決めるため, 問題に応じて物理的に境界条件が要請される場合があります. 例えば Appendix 1 で紹介するように, 両端が閉じた亀裂の場合には $u(\pm) = 0$ であり, あるいは別の問題では $u(-1) = 0, u(+1) = 1$ という状況もあり得ますが, 今回は前者の場合を考えます. すると $x_0 = -1$, $x_N = +1$ より結局, $i, j = 1, 2, ..., N-1$ に対し
\begin{align}
f_i := & f\left(x_i\right), \\
u_j := & u\left(x_j\right), \\
A_{ij} := & K\left(x_i, \xi_j\right) - K\left(x_i, \xi_{j+1}\right), \\
K_{ij} := & \frac{\lambda}{\pi} \frac{1}{\xi_j - x_i}
\end{align}
として,
$$
\sum_{j = 1}^{N-1} A_{ij} u_j = f_i
$$
という密行列 $A_{ij}$ を伴う線形方程式をソルバに渡すことになります.
さて, 数値解を構成する目処はついたのですが, このままでは解の精度が低いことは明らかです. というのも, 微分を中央差分で近似する操作は2次精度ですが, そもそも積分を長方形近似しているので, 全体としては長方形近似による1次精度しか期待できないからです. これを補うために, 積分区間を非等間隔にすることを考えます. 解の積分表現によれば, Airfoil 方程式の解 (ここでは $u'$) は一般に端点近傍で $r^{-1/2}$ のオーダーの特異性を持つことでしょう5. ただしここで $r ( \ll 1)$ は端点からの距離です. つまりこれを積分した $u$ は $r^{1/2}$ の特異性を持つことが期待されます. そこで, 分割幅が端点近傍で $r^{1/2}$ に近づくように設定します. 具体的には
\begin{align}
\begin{cases}
x_i = -\cos\left(\frac{i}{n} \pi\right), \, (i = 0, 1, ..., N) \\
\xi_i = -\cos\left(\frac{i-0.5}{n} \pi\right), \, (i = 1, 2, ..., N )
\end{cases}
\end{align}
を採用し, 数値計算の精度を調べます. 誤差評価のため, 今回は最も単純な場合
$$
f(x) = -1
$$
を考えます. これを解の公式に代入して計算すると, 厳密解として
$$
u = \sqrt{1 - x^2}
$$
を得ることができます. そこで数値計算結果をこの曲線と比較し, 相対誤差
$$
e := \max_{1 \le i \le n-1} \frac{ \left| u_\textrm{numerical}(x_i) - u_\textrm{exact}(x_i) \right| }{ u_\textrm{exact}(x_i) }
$$
が $N$ の増大と共にどのように減ってゆくかを調べることにします. 等分割の場合には先ほど考えたように, 分子の絶対誤差は $O\left(N^{-1}\right)$ である一方, 分母は端点で $O\left(N^{-1/2}\right)$ ですから,
$$
e \sim O\left(N^{-1/2}\right)
$$
が予想されますが, 非等分割の場合にはこれがどの程度改善するかを確認しましょう.
下図(図2とします)の左は $N=32$ の非等分割における数値解と厳密解との比較です. 見た目には十分に厳密解が近似できていることが確認できます. また端点近傍ほど分割が細かくなっている様子もわかるでしょう.
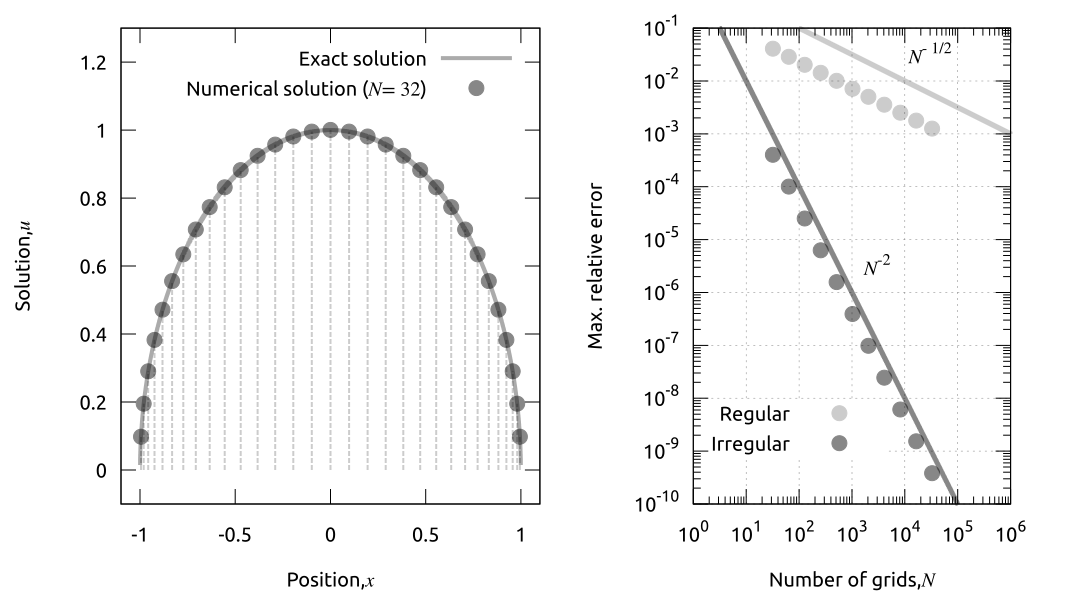
図2の右は等分割と非等分割それぞれの場合に $N$ を増やして相対誤差の変化を見たものです. 等分割については予想通りのオーダーで, 非常に収束が悪いことがわかりますが, 非等分割では2次のオーダーで収束しているようです. 言語は Fortran 2008, コンパイルには ifort v.18.0.2 を用い, DGESV で線形方程式を倍精度で解いていますが, $N = 32,768$ まで増やした時点でメモリ使用量が20GBを超えるくらいになったので, それ以上は試していません. そんなにメモリを使っておいて単精度+2桁くらいしか出ていないというのも情けないので, いずれは数値微積分の離散化に高精度な手法を用いて収束レートを改善するなどしたいところです.
2. Carleman 型方程式の場合
続いては Carleman 型方程式を扱いますが, 先ほど同様, $u$ ではなく $u'$ を未知関数とし,
$$
a(x) u'(x) - \lambda \int_{-1}^{+1} \frac{u'(\xi)}{\xi - x} \frac{d\xi}{\pi} = f(x)
$$
を考えます. この方程式の解は複雑ながら,
\begin{align}
u'(x) = & \frac{f(x)}{a(x)} \cos{\theta(x)} \\
& + \frac{e^{\tau(x)} \sin{\theta(x)}}{\lambda} \int_{-1}^{+1} \frac{\sin{\theta(\xi)}}{e^{\tau(\xi)}} \frac{f(\xi)}{\xi -x} \frac{d\xi}{\pi} \\
& + C \frac{e^{\tau(x)} \cos{\theta(x)}}{1-x}
\end{align}
と求めることができ2, ここで $\theta$, $\tau$ はそれぞれ
\begin{align}
\theta(x) := & \arctan{\frac{\lambda}{a(x)}}, \, (0 < \theta < \pi) \\
\tau(x) :=& \int_{-1}^{+1} \frac{\theta(\xi)}{\xi - x} \frac{\xi}{\pi}
\end{align}
という関数, $C$ は任意定数です6. この積分表現を数値的に直接評価しようとすると, やはり先程のように DE 法などが必要になりますが, 被積分関数に含まれる $\tau(x)$ もまた積分で書かれているので, DE 法の分点上での $\tau$ の値を求めるためにまた DE 法を使う…という2段階の手間がかかります7. 流石に扱いに困るので, やはり最も簡単な場合として $a \equiv 1$, $f \equiv 1$ とすると,
$$
u'(x) - \lambda \int_{-1}^{+1} \frac{u'(\xi)}{\xi - x} \frac{d\xi}{\pi} = 1
$$
の解として
$$
u'(x) = \sin{(\pi \alpha)} \frac{1 - 2 \alpha - x}{(1-x)^{1-\alpha} (1+x)^{\alpha}}
$$
およびその積分 $u(x) := \int_{-1}^x u'(\xi) d\xi$ により
$$
u(x) = 2 \sin{(\pi \alpha)} \left[ B\left(\frac{1+x}{2};1-\alpha,1+\alpha\right) - \alpha B\left(\frac{1+x}{2};1-\alpha,\alpha\right) \right]
$$
を得ます. ただしここで
\begin{align}
\alpha = & \frac{1}{\pi} \arctan{\lambda}, \\
B(x;a,b) = & \int_0^x t^{a-1} (1-t)^{b-1} dt, \textrm{(不完全 beta 関数)}
\end{align}
であり, 定数 $C$ の任意性は, 先ほど同様 $u(\pm 1) = 0$ を満たすように定めました. 実際, (完全) beta 関数を用いて
$$
u(+1) = 2 \sin{(\pi \alpha)} \left[ B(1-\alpha,1+\alpha) - \alpha B(1-\alpha,\alpha) \right]
$$
と書くことができ, (完全) beta 関数の漸化式
$$
(x+y) B(x,y+1) = y B(x,y)
$$
を用いると $u(+1) = 0$ が分かります.
前半に紹介した有限 Hilbert 変換の反転公式を含め, これらの厳密解を得るには積分区間を複素平面上の分岐切断と見做し, 複素関数が分岐切断の両側で不連続な値を取ると考えて, この不連続分布を解に対応させます. そしてこの分岐切断が亀裂, あるいは翼に相当するというわけです. このような特異積分方程式論的アプローチは Muskhelishvili や Tricomi の教科書2に詳しく纏まっており, いずれもこの分野のバイブルといった趣ですが, 日本語の文献や最近書かれた文献は乏しく, 今ではかなりマイナーな理論です. Qiita 向きの話題かどうかはわかりませんが, 私の最も好きな数学理論なので, いずれどこかで紹介したいと思います.
さて, ここからは積分方程式を直接離散化して数値解を構成します. 特異積分項の離散化は既に先ほど行なったので, 1階微分作用素を行列形式で書くことができれば, これを $D$ として線形方程式
$$
\sum_{j = 1}^{N-1} \left(D_{ij} - A_{ij}\right) u_j = f_i
$$
を解くだけです. ただし, 先ほどは $u'$ を離散化するにあたり, 点列 $\xi_j$ と $x_i$ が互い違いになっていることから, $x_{j-1}$ と $x_j$ で定義された $u$ を用いて $\xi_j$ で定義された微分 $u'$ を中央差分近似しました. しかし行列 $D$ は点列 $x_j$ で定義された $u_j$ から, 同じく点列 $x_i$ で定義される $u_i'$ を生成しないといけません. しかもせっかく特異積分項が2次精度で近似出来るのですから, 端点の処理も含め, $D$ も2次精度が欲しいところです. そこで 点 $x_i$ における微分係数 $u_i'$ を近似するために, 図1の青線のように3点 $(x_{i-1}, u_{i-1}), (x_i, u_i), (x_{i+1},
u_{i+1})$ を通る2次関数を求め, この2次関数の $x = x_i$ における微分係数を $u_i'$ とします. ただし端点では, $u_1'$ を決めるために $x_1, x_2, x_3$ での値を補間する2次関数の $x = x_1$ における微分係数を, $u_{N-1}'$ を決めるために $x_{N-3}, x_{N-2}, x_{N-1}$ での値を補間する2次関数の $x = x_{N-1}$ における微分係数を, それぞれ採用します. 積分点が等間隔でないことを考慮して, 若干面倒ですが計算して実装したものが, Appendix 2 に示す Fortran コードのうち, generateDiffMatrix サブルーチンです. グローバル変数 N は分割数で, 分点座標の配列 x(0:N) は生成済みとします. もうちょっとスマートに書きたいものですが…
そしてそのコードを用いた数値計算結果の紹介です. 下図を図3とします.
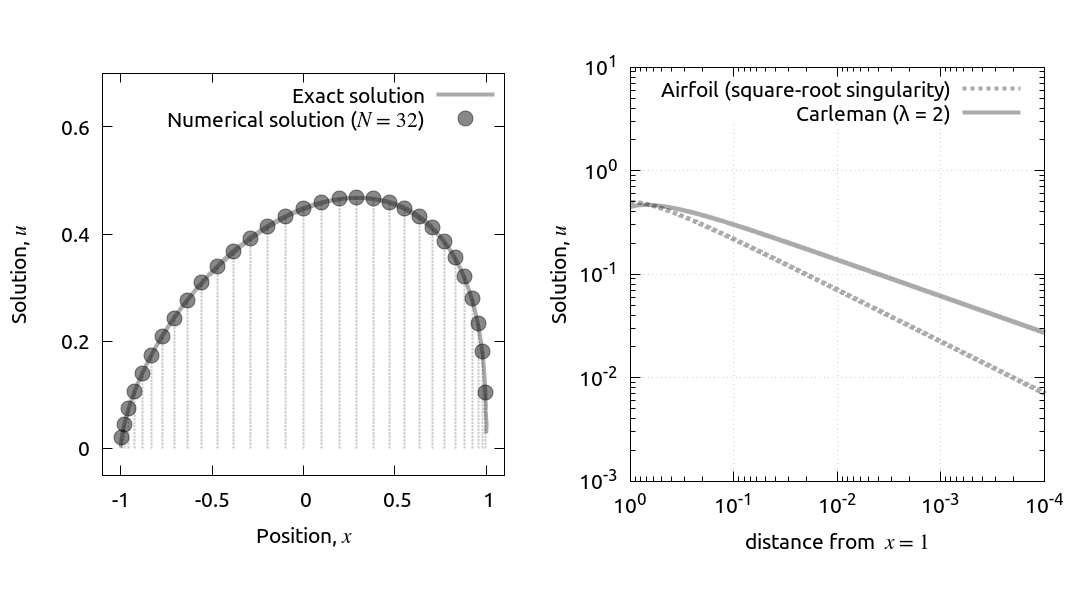
$\lambda = 2.0$ の場合を仮定してみましたが, 厳密解と数値解は$N = 32$ でもよく一致しているように見えます. Airfoil 方程式とは異なる特徴として, 解が左右非対称である様子がわかります. ここで, 厳密解は Gnuplot で関数
lambda = 2.0
a = atan(lambda)/pi
B(p,q,x) = gamma(p)*gamma(q)/gamma(p+q)*ibeta(p,q,(1+x)/2)
u(x) = 2*sin(pi*a)*(B(1-a,1+a,x) - a*B(1-a,a,x))
を定義してプロットしました. gamma 関数が登場するのは, Gnuplot の不完全 beta 関数 ibeta が0から1の範囲に規格化されており, 従って振幅を与えなければいけないことと, そのための完全 beta 関数が用意されていないことによるものです. しかし厄介なことに, Gnuplot で計算可能な gamma 関数およびそれを用いた上記関数は, どの程度の数値精度を有するのかよくわかりません. 実際, 以前別の研究テーマで beta 関数を計算していたとき, けっこうあっさりと発散する領域が見えていました. 従って, 本当はここでも先ほど同様に誤差の評価をすべきところですが, そのためには不完全 beta 関数を高精度に計算するためのコーディングが必要になるので諦めます. ただし先ほど評価点を Airfoil 方程式の解の端点における特異性から決めたので, これが変わってしまった以上は精度が落ちていることは間違いありません.
代わりと言ってはなんですが, ここでは(精度を疑ったくせに)厳密解を用いて, 領域右端$x = +1$ からの距離に応じた $u$ の値を両対数グラフにしてみました(図3右). グラフの右に行くほど距離も振幅も小さくなります. ここで先程の Airfoil 方程式の解(点線)と比べると, 端点近傍の振る舞いが大きく異なることがわかります. 領域端において, Airfoil 方程式の解の特異性は$r^{1/2}$ ですが, Carleman 型方程式の解の特異性は 右端では $r^{\alpha}$, 左端では$r^{1-\alpha}$ であることがわかっています. これは非常に興味深い振る舞いで, 破壊力学では亀裂端での解の特異性が応力の強さを決めますが, この特異性が $1/2$ である通常の亀裂と異なり, 両側の物性が異なるせん断亀裂8では, 一方の端で強い応力集中が生じ, 他方では弱い応力集中しか生じないということが, このような解析から指摘されています.
終わりに
1次元の有界区間における特異積分方程式の例として, Airfoil 方程式, および Carleman 型方程式の数値解を構成しました. 厳密解との比較のため, 非斉次項 $f$ や係数関数 $a$ が定数である場合しか扱いませんでしたが, これらが関数であっても, 積分区間内に悪さをする特異点がないものであれば問題なく数値解が計算できます. 実際の研究では, 亀裂端で応力が発散するのを回避するような $a$ や$f$ を見つけるなどの工夫が要求される場合もあります.
Appendix 1. 2次元静弾性体内の亀裂による Airfoil 方程式の導出
最後にかいつまんで, Airfoil 方程式の導出を紹介しておきます. と言っても線形弾性破壊力学の知識は必ずしもメジャーではないため, 簡単な場合として, ここでは2次元 $x$-$y$ 平面についての静的面外変形を題材にします. 静的というのは運動方程式の慣性項を無視するという意味で, 面外変形というのは, この平面に直交する $z$ 方向の変位だけを考えるという意味です.これは3次元弾性体の運動方程式である Navier の式
$$
\rho \partial_t^2 \boldsymbol{u} = \left( \lambda + 2 \mu \right) \nabla \left( \nabla \cdot \boldsymbol{u} \right) - \mu \nabla \times \left( \nabla \times \boldsymbol{u} \right)
$$
において,
$$
\partial_t^2 \boldsymbol{u} = 0, \
\partial_z \boldsymbol{u} = 0
$$
と仮定することで, 変位ベクトル $\boldsymbol{u}$ の $z$ 成分 $u_z$ について得られる2次元 Laplace 方程式
$$
\Delta u_z = 0 , \left(ただし \Delta = \partial_x^2 + \partial_y^2 \right)
$$
によって記述される問題なので, 他の物理現象でもよく知られたモデルに見えます. しかし独自の境界条件により, 領域内部で同様の方程式を満たす, 例えば静電場や静磁場とは異なる基本解を持つという特徴があります. 今, 原点 $\left(x, y\right) = 0$ において, $x$ 軸に沿う無限小の亀裂があるとします. 亀裂の定義を「両側で変位に食い違いのある面」とすると, このことは先の方程式と境界条件とを併せて
\begin{align}
\begin{cases}
\Delta u_z = 0, & (x,y) \ne 0 \\
\lim_{y \downarrow 0} u_z - \lim_{y \uparrow 0} u_z = \delta(x), & y = 0 \\
\lim_{y \downarrow 0} \mu \partial_y u_z - \lim_{y \uparrow 0} \mu \partial_y u_z = 0, & y = 0 \\
u_z \to 0, & \left| (x,y) \right| \to \infty
\end{cases}
\end{align}
(ただし $\mu$ は剛性率) と書くことができます. ここで第2式が原点に局在する単位量の変位食い違いを表わし, 第3式は「亀裂があってもなくても(特に力源は無いので) $x$ 軸を挟んで応力は連続」の意味, 第4式は亀裂の影響が無限遠に及ばないことを表わします. さてここで $x$ 方向の Fourier 変換を
$$
\widehat{u}(k) := \int_{-\infty}^{+\infty} u(x) , e^{i k x} , dx
$$
で定め, これを先の方程式に施せば,
\begin{align}
\begin{cases}
\partial_y^2 \widehat{u}_z = \xi^2 \widehat{u}_z, & y \ne 0 \\
\lim_{y \downarrow 0} \widehat{u}_z - \lim_{y \uparrow 0} \widehat{u}_z = 1, & y = 0 \\
\lim_{y \downarrow 0} \partial_y \widehat{u}_z - \lim_{y \uparrow 0} \partial_y \widehat{u}_z = 0, & y = 0 \\
\widehat{u}_z \to 0, & \left| (k,y) \right| \to \infty
\end{cases}
\end{align}
が得られ, 第1式と第4式より常微分方程式の解
$$
\widehat{u}_z = A^\pm e^{- | k | | y |},
$$
を得ます. ただし $A^\pm$ は $y$ の符号に応じた量です. 一般には $A^\pm$ は $k$ の関数であっても良いのですが, 上式の第2および3式より,
$$
A^+ = +\frac12, \quad A^- = -\frac12
$$
であることがわかります. これに Fourier 逆変換
$$
u(x) = \frac{1}{2 \pi} \int_{-\infty}^{+\infty} \widehat{u}(k) , e^{- i x k} , dk
$$
を施して, 変位場の解
$$
u_z = \frac{y}{2 \pi \left( x^2 + y^2 \right)},
$$
そしてここから, $y \to 0$ におけるせん断応力の $xz$ 成分
$$
\lim_{y \to 0} \mu \partial_y u_z = \frac{\mu}{2 \pi x^2}
$$
を得ます. 線形弾性破壊力学というのは, この点亀裂の線形な重ね合わせにより任意の長さ・形状を持つ亀裂による変形と応力が表現できるという立場です. したがって, $-1 < x < +1$ の範囲に亀裂が存在し, その上の変位食い違い量が $D(x)$ という分布を持つとき, $x$ 軸上のせん断応力分布は
$$
\sigma_{xz}(x) = \frac{\mu}{2} \int_{-1}^{+1} \frac{D(\xi)}{\left( \xi - x \right)^2} \frac{d\xi}{\pi}
$$
と書けると考えます. ここで問題になるのは, 右辺の積分核が $x^{-2}$ のオーダーを持っており, 一見すると主値を考慮しても積分が存在しないことです. これは, そもそも積分核が Dirac の $\delta$ 関数を含む偏微分方程式の基本解であり, 従って通常の意味の関数とは異なる Schwartz 超関数であることと深く関係します. Schwartz 超関数論については様々な入門書があるのでそちらを参照して頂くとして, 超関数については自然な微分の定義があり, それは要するに
$$
\int_{-1}^{+1} \frac{D(\xi)}{\left( \xi - x \right)^2} \frac{d\xi}{\pi} = - \int_{-1}^{+1} \frac{D'(\xi)}{\xi - x} \frac{d\xi}{\pi}
$$
と部分積分してしまえばいいでしょう, というものです. これで静弾性の面外方程式から, Airfoil 方程式
$$
\sigma_{xz}(x) = - \frac{\mu}{2} \int_{-\infty}^{+\infty} \frac{D'(\xi)}{\xi - x} \frac{d\xi}{\pi}
$$
が得られたことになります.
Appendix 2. Fortran ソースコード
以下に示すコードのうち, サブルーチン solveLinearEquation は別ファイルのモジュール wrapper_DGESV 内で記述されているのですが, これは単に Intel MKL から利用可能な DGESV の引数を隠蔽して簡潔にするためだけのラッパーです.
module parameters
implicit none
double precision, parameter :: pi = acos(-1d0)
! Number of grids
integer, parameter :: n = 2**5
double precision, parameter :: lambda = 2d0
! .true. gives simple regular grids, while .false. results in an accurate numerical solution.
logical, parameter :: isRegularInterval = .false.
end module parameters
program main
use parameters
use wrapper_DGESV
implicit none
integer :: i
double precision :: x(0:n), &
& A(1:n-1,1:n-1), &
& u(1:n-1), &
& f(1:n-1), &
& D(1:n-1,1:n-1)
call calcKernel(x,A)
! In the following, x(0) and x(n) are eliminated because u'(0) and u'(n) diverge therein.
call generateDiffMatrix(D,x(1:n-1))
! Give an arbitrary distribution if the inhomogeneous term f is not a constant.
f = 1d0
! Solving f=(D-A)u w.r.t. u
call solveLinearEquation(f,D-A,u)
open(00,file="u_Carleman.dat")
write(00,'(2e25.15e3)') ( (x(i), u(i)), i = 1,n-1 )
close(00)
stop
contains
subroutine calcKernel(x,A)
double precision, intent(out) :: x(0:n), &
& A(1:n-1,1:n-1)
double precision :: xi(1:n), &
& K(1:n-1,1:n)
integer :: i, j
if (isRegularInterval) then
forall(i=0:n) x(i) = 2d0*dble(i)/dble(n)-1d0
forall(i=1:n) xi(i) = ( x(i-1) + x(i) ) / 2d0
else
forall(i=0:n) x(i) = -cos(pi*dble(i)/dble(n))
forall(i=1:n) xi(i) = -cos(pi*(dble(i)-0.5d0)/dble(n))
end if
forall(i=1:n-1, j=1:n) K(i,j) = 1d0/(xi(j)-x(i))
forall(i=1:n-1, j=1:n-1) A(i,j) = K(i,j)-K(i,j+1)
A = lambda/pi*A
return
end subroutine calcKernel
subroutine generateDiffMatrix(D,x)
double precision,intent(out) :: D(:,:)
double precision,intent(in) :: x(:)
double precision :: h(0:2)
integer::i, m
m = size(x)
! 2nd order forward difference in the left edge
h(0:2) = L(x,2)
D(1,1:3) = (/ -h(2)-h(0), +h(0)+h(1), -h(1)+h(2) /)
! 2nd order central difference for internal points
do i = 2, m-1
h(0:2) = L(x,i)
D(i,i-1:i+1) = (/ h(2)-h(0), h(0)-h(1), h(1)-h(2) /)
end do
! 2nd order backward difference in the right edge
h(0:2) = L(x,m-1)
D(m,m-2:m) = (/ h(0)-h(2), -h(0)-h(1), h(1)+h(2) /)
return
end subroutine generateDiffMatrix
function L(x,i)
double precision,intent(in) :: x(:)
integer,intent(in) :: i
double precision :: L(0:2)
L(0) = 1d0 / ( x(i) - x(i-1) )
L(1) = 1d0 / ( x(i+1) - x(i) )
L(2) = 1d0 / ( x(i+1) - x(i-1) )
return
end function L
end program main
余談ですが, Fortran コードにおいて, グリッド座標配列 x(0:n) は一度定義したら変更しないので, 冒頭の変数定義 module で
double precision, parameter :: x(0:n) = (/ (dble(2*i)/dble(n)-1d0, i=0,n) /)
とし, グローバル変数としたい…と思っていたのですが, ifort では n の値が数万くらいからコンパイル時間が非線形に増大するので諦めました. gfortran ではそこまで問題ではないのですが, 何故…
-
日本語訳不明. "Airfoil equation" でも Google ヒット数3千件未満で, しかも今世紀の文献は希少. 物理的導出については Airfoil - Wikipedia ↩
-
包括的な数学理論は Muskhelishvili, N.I. (1953), Singular Integral Equations に纏められており, Airfoil 方程式や Carleman 型方程式についての実軸上の具体的な解の構成は Tricomi, F.G. (1957), Integral Equations に詳しいのですが, 忘れられつつある理論です. ↩ ↩2 ↩3 ↩4
-
例えば端点の特異性だけを取り出して, 積分 $\int_0^1 \sqrt{x} dx = \frac32$ を Simpson 公式などで数値的に実行してみるとすぐにわかります. 一般に Newton-Cotes の公式による数値積分の誤差評価には被積分関数の微分が影響しますが, これが発散していることに難があります. ↩
-
Takahasi, H., and Mori, M (1974), Double exponential formulas for numerical integration, Publ. Res. Inst. Math. Sci. 9, 721–741. / 日本語による解説は シキノート ↩
-
破壊力学では Square-root singularity と呼ばれ, 亀裂先端で応力が発散する強さを表わしています. 実際には無限大の応力に耐える物質は無いはずで, 特異点近傍では塑性化などの非弾性変形が生じていると考えるべきですが, その領域が十分小さいとみなすのが線形弾性破壊力学です. なお応力は無限大でも, 亀裂が単位長さ伸展する際に弾性体から解放されるポテンシャルエネルギーはちゃんと有界であることが示されます. そのための積分を J-integral と呼びます. ↩
-
DE 法は特異点を原点に平行移動して持ってこないといけないという制約があります. 件の積分は積分区間の両端が特異点なので, 積分を2つに分割してそれぞれ別個に評価するとか, $\tau(x)$ を求めるのに $\xi = x$ での扱いに工夫がいるとか…昔論文で実行したことがありますが, とにかく地味に手間のかかる計算です. ↩
-
開口ではなく滑りを伴なう亀裂, 例えば地震を引き起こす地下の断層運動など. ↩