Pythonでベイズ線形回帰を実装してみた

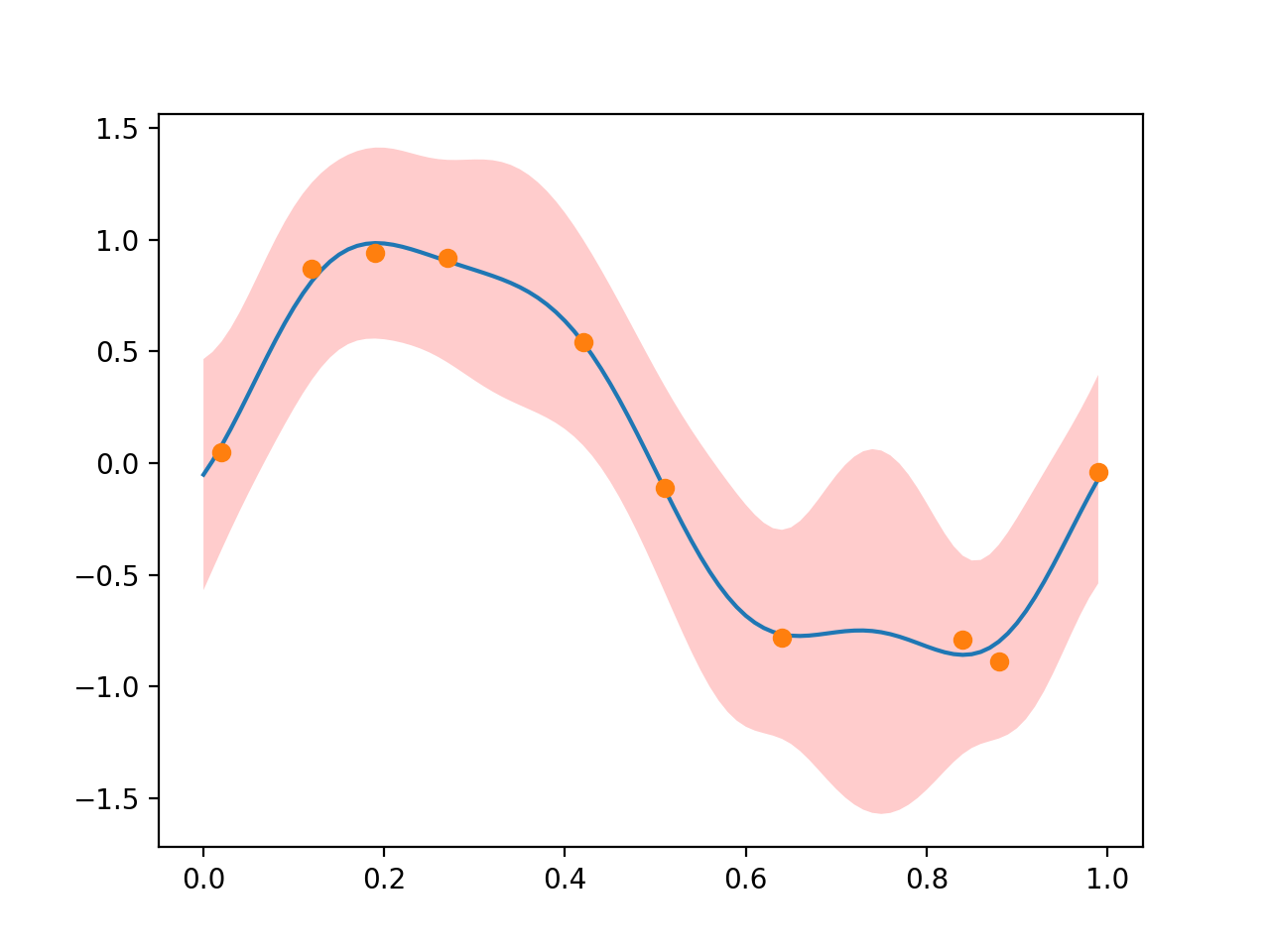
#ベイズ線形回帰の目的
前回の記事（ベイズ線形回帰）でベイズ線形回帰の概略をざっくりまとめたのだが、今回は実際にその過程をPythonで実装してみたのでこれまたざっくりまとめてみようと思う。
線形回帰の目的というのが、入力xに対して出力yが
$$y=x^Tw+\epsilon$$
という形でモデリングされるという仮定に基づき、新たな入力に対応する尤もらしい出力を返せるようなwを推定したいというものだ。
ここで自分が一つ勘違いしてたことがあった。
線形回帰というものは今まで入力xに対して線形だと思っていたのだが正しくはパラメータwに対して線形だということを最近知った。
つまり入力xに基底関数を噛ませて非線形にしても、wの一次線形和（この言い方で合ってる？）であれば線形回帰と呼ぶのだろう。
このwの値を直接求めるのが普通の線形回帰、一方のベイズ線形回帰はwが従う確率分布を推定する。そのために訓練データが得られる前のwの事前分布を$N(0,\Sigma_p)$定め、そこから訓練データが得られた後の事後確率を求める。
その結果
$$w|y,X \ \~ N\left(\frac{1}{\sigma_n^2}\left(\frac{1}{\sigma_n^2}XX^T+\Sigma_p^{-1} \right)Xy,\frac{1}{\sigma_n^2}XX^T+\Sigma_p^{-1} \right)$$
$\sigma_n^2$はノイズの分散である。
また今回は基底関数としてガウス関数を用いた。ガウス関数の式は以下の通りである。
$$\Phi(x) = exp\left(-\frac{(x - s)^2}{2s^2} \right)$$

#コード

import numpy as np
import matplotlib.pyplot as plt

X = np.array([0.02, 0.12, 0.19, 0.27, 0.42, 0.51, 0.64, 0.84, 0.88, 0.99])
y = np.array([0.05, 0.87, 0.94, 0.92, 0.54, -0.11, -0.78, -0.79, -0.89, -0.04])

#基底関数 ガウス関数
def phi(x):
    #ガウス関数のバンド幅
    s = 0.1
    return np.append(1,np.exp(-(x - np.arange(0,1+s,s))**2/(2 * s * s)))

PhiX = np.array([phi(x) for x in X])

#1/sigma_n^2 = alpha
alpha = 9.0
#Sigma_p^-1 = beta * I
beta = 0.1

#p
A = alpha * np.dot(PhiX.T,PhiX) + beta * np.identity(PhiX.shape[1])
w_bar = alpha * np.dot(np.dot(np.linalg.inv(A),PhiX.T),y)

xlist = np.arange(0,1,0.01)
ylist = [np.dot(w_bar,phi(x)) for x in xlist]
#予測分布の分散
s_2 = [1.0/alpha + np.dot(np.dot(phi(x),np.linalg.inv(A)),phi(x).T) for x in xlist]

s = np.sqrt(s_2)
predict_upper = ylist + s
predict_lower = ylist - s
plt.plot(xlist,ylist)
plt.plot(X,y,'o')
plt.fill_between(xlist,predict_upper,predict_lower,facecolor='r',alpha=0.2)
plt.show()

#実行結果