概要
ニューラルネットワークを学ぶ第一歩として、パーセプトロンの仕組みと実装を簡潔に解説します。
Elixir と Nx を使って、LiveBook 上で動かせるコードとともに進めていきます。
本記事は以下の書籍を参考にしています。
LiveBook 上で 実装を行いますが、セットアップ方法については、公式サイトをご参照ください。
また、Nxの関数の詳細な説明は省略します。
環境
本記事の内容は、以下の環境で動作確認をしています。
- macOS Sequoia 15.5
- Livebook v0.16.1
リポジトリ
この記事で紹介したコードは、以下の LiveBook ファイルで試せます。
本題
ニューラルネットワークについてGoogle 画像検索で検索すると、入力層、中間層、出力層という単語が載っている画像がヒットします。(ここでは載せませんが)
画像内の⚪︎はニューロンとかノードと呼ばれます。
どの画像もニューロンから伸びた矢印が、中間層の別のニューロンを指しており、最終的に出力層のニューロンに集約するのがわかるかと思います。
入力層のニューロンが中間層のニューロンを指すとき、パーセプトロンという関数を実行した値がその中間層のパーセプトロンが後続の層のニューロンに入力する値となります。
パーセプトロンとは
パーセプトロンとは、入力を受け取って出力するかしないかを決める関数のことです。
計算には入力、重み、バイアスを使用します。
入力と重みを乗算して、バイアスを総和したものが 0 を超えた時に1を出力し、超えない時に0を出力します。
このように 1 を出力することを 発火 と呼び、重みとバイアスを調整することで発火をコントロールできます。
以下に、単純な論理回路を実装する例を示します。
関数の実装
以下はANDゲートという論理回路を実装したものになります。
def and_gate(x1, x2) do
x = Nx.tensor([x1, x2])
w = Nx.tensor([0.5, 0.5])
b = Nx.tensor(-0.7)
temp = Nx.add(Nx.dot(x, w), b)
if Nx.to_number(temp) > 0 do
1
else
0
end
end
ここでは、重みとバイアスはそれぞれ以下のようになっています。
- 重みは、
[0.5, 0.5] - バイアスを
-0.7
この関数に引数として 1, 1 を渡した時、重みと乗算(Nx.dot/2)して、バイアスを足した(Nx.add/2)とき、結果は以下のようになります。
temp = Nx.add(Nx.dot(x, w), b)
IO.inspect(temp)
#Nx.Tensor<
f32
0.30000001192092896
>
0 を超えるので発火するため、1 を出力することになります。
IO.puts Gate.and_gate(1,1)
1
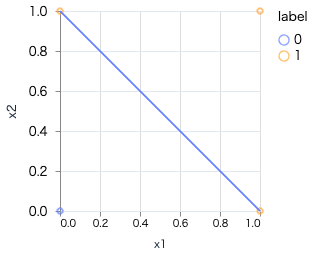
線形図に表すと以下のようになります。

出力のコントロールの例
先ほどの関数において、重みとバイアスと変更してみます。
ここでは、重みを[-0.5, -0.5]、バイアスを0.7に設定しました。
def nand_gate(x1,x2) do
x = Nx.tensor([x1, x2])
w = Nx.tensor([-0.5, -0.5])
b = Nx.tensor(0.7)
temp = Nx.add(Nx.dot(x, w), b)
if Nx.to_number(temp) > 0 do
1
else
0
end
end
すると先ほどは違う出力になりました。
IO.puts Gate.nand_gate(1,1)
0
このように出力を調整することで、NANDゲートが完成しました。
まとめ
パーセプトロンでは、上記のほかORを加えた3つの論理回路が実装できます。
defmodule Gate do
def and_gate(x1, x2) do
x = Nx.tensor([x1, x2])
w = Nx.tensor([0.5, 0.5])
b = Nx.tensor(-0.7)
temp = Nx.add(Nx.dot(x, w), b)
if Nx.to_number(temp) > 0 do
1
else
0
end
end
def or_gate(x1,x2) do
x = Nx.tensor([x1, x2])
w = Nx.tensor([0.5, 0.5])
b = Nx.tensor(-0.3)
temp = Nx.add(Nx.dot(x, w), b)
if Nx.to_number(temp) > 0 do
1
else
0
end
end
def nand_gate(x1,x2) do
x = Nx.tensor([x1, x2])
w = Nx.tensor([-0.5, -0.5])
b = Nx.tensor(0.7)
temp = Nx.add(Nx.dot(x, w), b)
if Nx.to_number(temp) > 0 do
1
else
0
end
end
end
ANDの真理値表は以下のようになります。
| x1 | x2 | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
これらの論理回路は、1つの発火で表現できるものになり、線形で表現できるものになります。(AND, OR, NAND)


多層パーセプトロン
多層パーセプトロンとは、先ほどのパーセプトロンを重ねたものを指します。
以下に、XORの論理回路を実装し、多層パーセプトロンの具体的な構造を解説します
XORの実装
XORは、単層のパーセプトロンでは表現できない非線形な論理です。
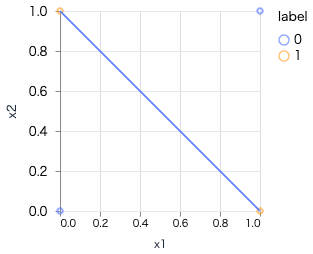
しかし、パーセプトロンを重ねる(多層にする) ことで、XOR を実現することが可能になります。
具体的には、前述の NAND、OR、AND を組み合わせることで、XOR を構築できます。
def xor_gate(x1, x2) do
s1 = Gate.nand_gate(x1, x2)
s2 = Gate.or_gate(x1, x2)
Gate.and_gate(s1, s2)
end
図で表すと、次のように2層構造のパーセプトロンになります。

このように、パーセプトロンを多層に重ねることで、より複雑な論理や関数を表現できるようになります。
まとめ
本記事ではニューラルネットワークの基礎となる、パーセプトロンについて、Elixir の Nx を使って、実装しながら解説しました。
パーセプトロンの要点を以下のようにまとめました。
- パーセプトロンは「入力を受けて発火するか決める関数」
- 重み・バイアスを使って出力を制御する
- 適切な重み・バイアスでAND・OR・NANDが実装可能
- 線形分離できないXORは、多層パーセプトロンで実装できる
今回はパーセプトロンの仕組みを深く理解するため、Axonは使用せず、Nxを使って細部まで実装を行いました。
次回は活性化関数について解説しつつ、ここからはAxonを用いた実装に移行していく予定です。