始めまして。Blitzです。
MATLABには潮流解析機能もあるらしいと聞いて、試しに使ってみました。
潮流解析問題とは
潮流解析問題とは、ある地点とある地点（例えば、発電設備と受電設備など）が接続されているときの電圧・位相・有効電力・無効電力を算出する問題です。これらの4変数のうち2変数が分かれば、残りの2変数も解けるという仕組みになります。
詳細な理屈は省略します（というより私自身も理解していない）が、ポイントは以下のところかと思います。
・各地点のパラメータを用いて、行列の方程式を作る。
・方程式は非線形方程式であり、厳密解を求めることはほぼ不可能。
・近似計算を行う。ニュートン・ラフソン法が一般的に利用される。
対象とする問題
対象とする潮流解析問題は令和元年の電験2種の試験、電力管理の問題2の問にします。系統から送電線を介して負荷に電力が供給されている状態です。
送電端は母線電圧が$V_s$であり、相差角が$\delta$で運転しています。受電端は母線電圧が$V_r$であり、相差角が0で運転しているとします（基準電圧ベクトルを受電端とします。）。送電端と受電端はインダクタンス$jX$の送電線で接続されているとします。負荷は有効電力$P$、無効電力$Q$を消費しているとします。
具体的なパラメータとして送電端電圧$V_s$ = 1.0pu、負荷有効電力$P$ = 0.5pu、負荷無効電力$Q$ = 0pu、送電線インピーダンス$X$ = 0.5puを与え、受電端電圧$V_r$および相差角$\delta$を求めることとします。
図1 対象とする潮流計算問題
一般式による解法（文字式）
ここからは、手計算をする場合にどのような手順で解くかを示します。
まず、送電線の電圧降下に注目します。電圧降下は以下の(1)式で表されます。ここで、$\dot{A}$のようなマークは複素数表示を表すこととします。
$\dot{V_s} －\dot{V_r} =\dot{I}×jX （1）$
ただし、相差角を考慮すると、(2), (3)式の関係があります。
$\dot{V_s} =V_s \cos{\delta} +j V_s \sin{\delta} (2)$
$\dot{V_r} =V_r (3)$
したがって、(1)式は(4)式のように展開できます。
$\dot{I} =\frac{\dot{V_s}－\dot{V_r}}{jX}=\frac{V_s \cos{\delta} +j V_s \sin{\delta} -V_r}{jX} (4)$
次に、受電端を考えます。受電端での皮相電力は以下の(5)式で表されます。ここで$\bar{A}$ のようなマークは複素数表示の複素共役を表すこととします。
$S =\bar{\dot{I}} ×\dot{V_r} (5)$
先ほどの(4)式から(6)式のように展開できます。
$S=\bar{\dot{I}} ×\dot{V_r} =\frac{V_s \cos{\delta} -j V_s \sin{\delta} -V_r}{-jX}V_r
= \frac{V_sV_r}{X}\sin{\delta} +j\frac{V_s V_r \cos{\delta} - V_r^2}{X} (6)$
したがって有効電力$P$と無効電力$Q$は以下の(7),(8)式で表されます。
$P = Re{(S)} =\frac{V_s V_r}{X}\sin{\delta} (7)$
$Q =Im{(S)} = \frac{V_s V_r \cos{\delta} - V_r^2}{X} (8)$
このように、電気回路理論を活用することで、送電端電圧$V_s$、受電端電圧$V_r$、相差角$\delta$から受電端の有効電力$P$および無効電力$Q$を計算することができます。
一般式による解法（具体的値の代入）
次に、(7),(8)式に具体的な値を代入することで、問題を解くことができます。
$0.5 = \frac{1× V_r}{0.5}\sin{\delta}$ ⇒ $Vr =\frac{1}{4 \sin{\delta}}$
$0 =\frac{1× V_r \cos{\delta} - V_r^2}{ 0.5}$ ⇒ $Vr =cosδ （V_r≠0のため）$
まずは、$V_r$を消去し、$\delta$を算出します。
$4\sin{\delta}\cos{\delta} = 1$ ⇒ $2\sin{2\delta} = 1$ ⇒ $\sin{2\delta} = 0.5$
⇒ $\delta$ = $\frac{π}{12}$ = $0.2618 [rad]= 15.000 [deg] $
次に、$\delta$に値を代入し、$V_r$を算出します。
$V_r = \cos{\frac{π}{12}} =\sqrt{\frac{1+\cos{\frac{π}{6}}}{2}}=0.96593[pu]$
このように、比較的簡単な潮流計算問題は手計算で求めることが可能です。
MATLAB/Simulinkでの解析
理論的な話は解説したので、次はMATLAB/Simulinkを用いて問題を解いていきます。
先ほどの問題は、単位法を用いた問題であり、あらゆる電圧で活用できる解になります。一方、MATLABは具体的な系統の問題を解くので、具体例を与えてあげる必要があります。
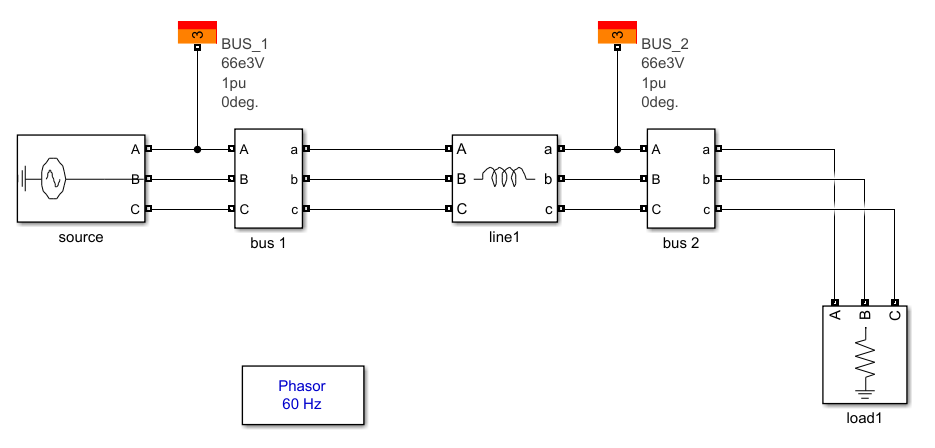
ここでは、シミュレーションモデルを図2のとおりとし、パラメータとしては以下の表1,2のようなモデルを検討します。
図2 MATLAB/Simulinkの解析モデル
表1 基準電圧と基準電力
| 単位法 | 非単位法 | |
|---|---|---|
| 基準電圧 Vb | 1.0pu | 66kV |
| 基準電力 Sb | 1.0pu | 100MVA |
表2 その他各種パラメータ
| 単位法 | 非単位法 | |
|---|---|---|
| 電源電圧 Vs | 1.0pu | 66kV |
| 電源周波数 f | 60Hz | |
| 送電線リアクタンスX | 0.5pu | 21.78Ω |
| 送電線インダクタンスL | 57.775mH | |
| 受電端有効電力 | 0.5pu | 50MW |
| 受電端無効電力 | 0pu | 0Var |
解析結果
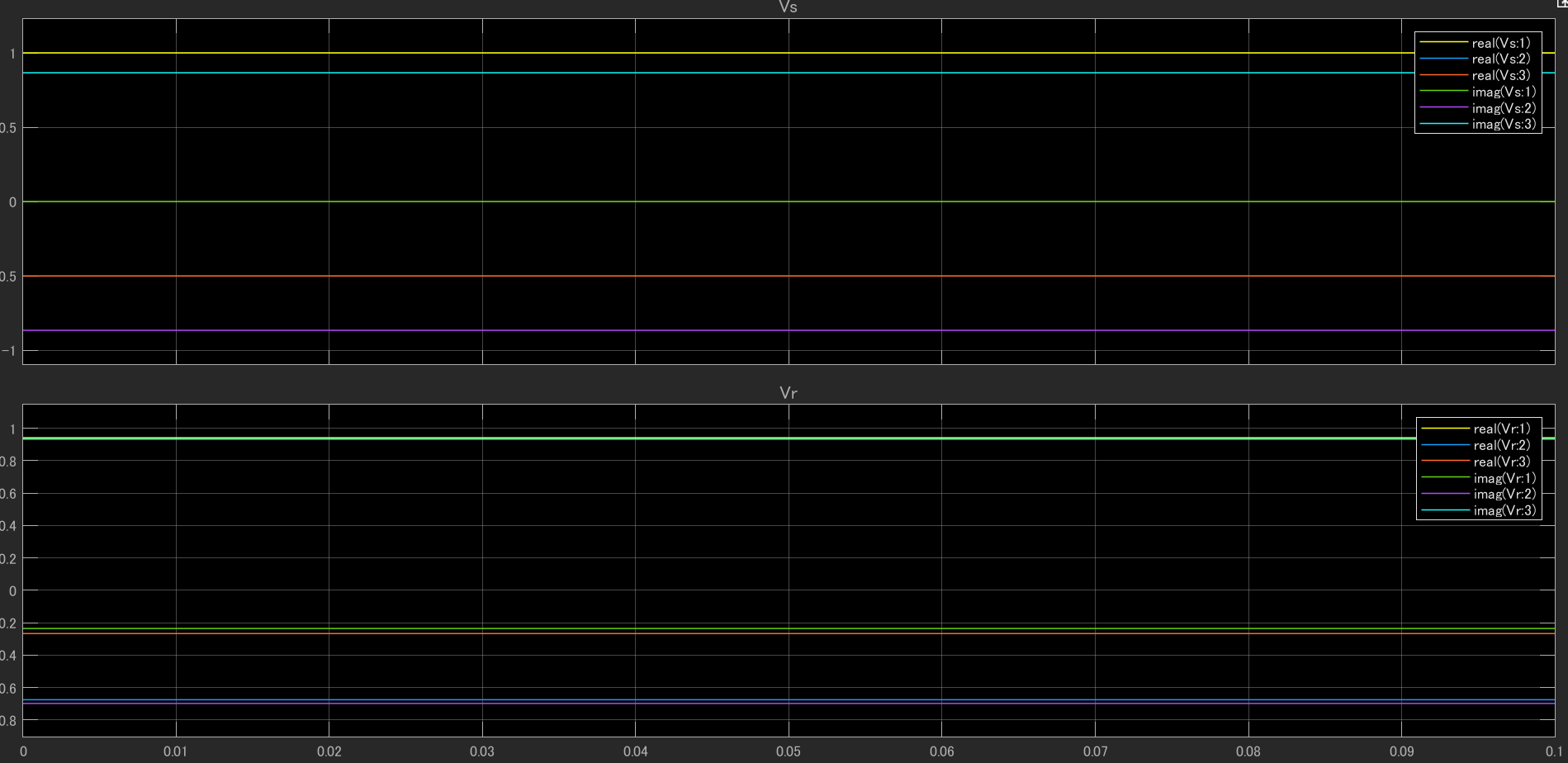
本解析をした場合の、電圧の時間変化をシミュレーションしました。図3は送電端の電圧と受電端の電圧をScopeにて測定した波形になります。3相交流電源の実数部と虚数部に分かれて、電圧がプロットされます。イメージは図4のようなものでしょうか。
図3 送電端電圧と受電端電圧の経時変化
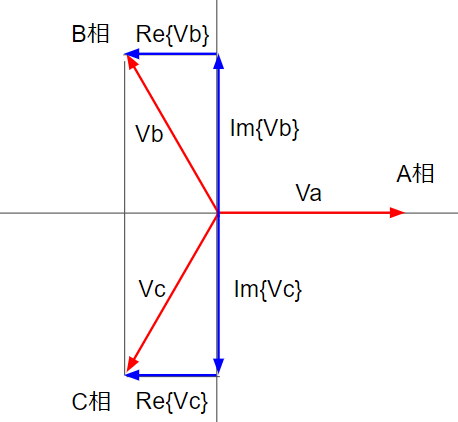
図4 Scopeに表示されているパラメータのベクトル図
潮流解析を行うには、PowerGuiの中のLoad Flow Analyzerを活用する必要があります。図5,6にLoad Flow Analyzerの様子を示します。Load Flow Analyzerを開いた時には、演算がされていないので、潮流計算結果を得たい場合にはComputeを実行しましょう。
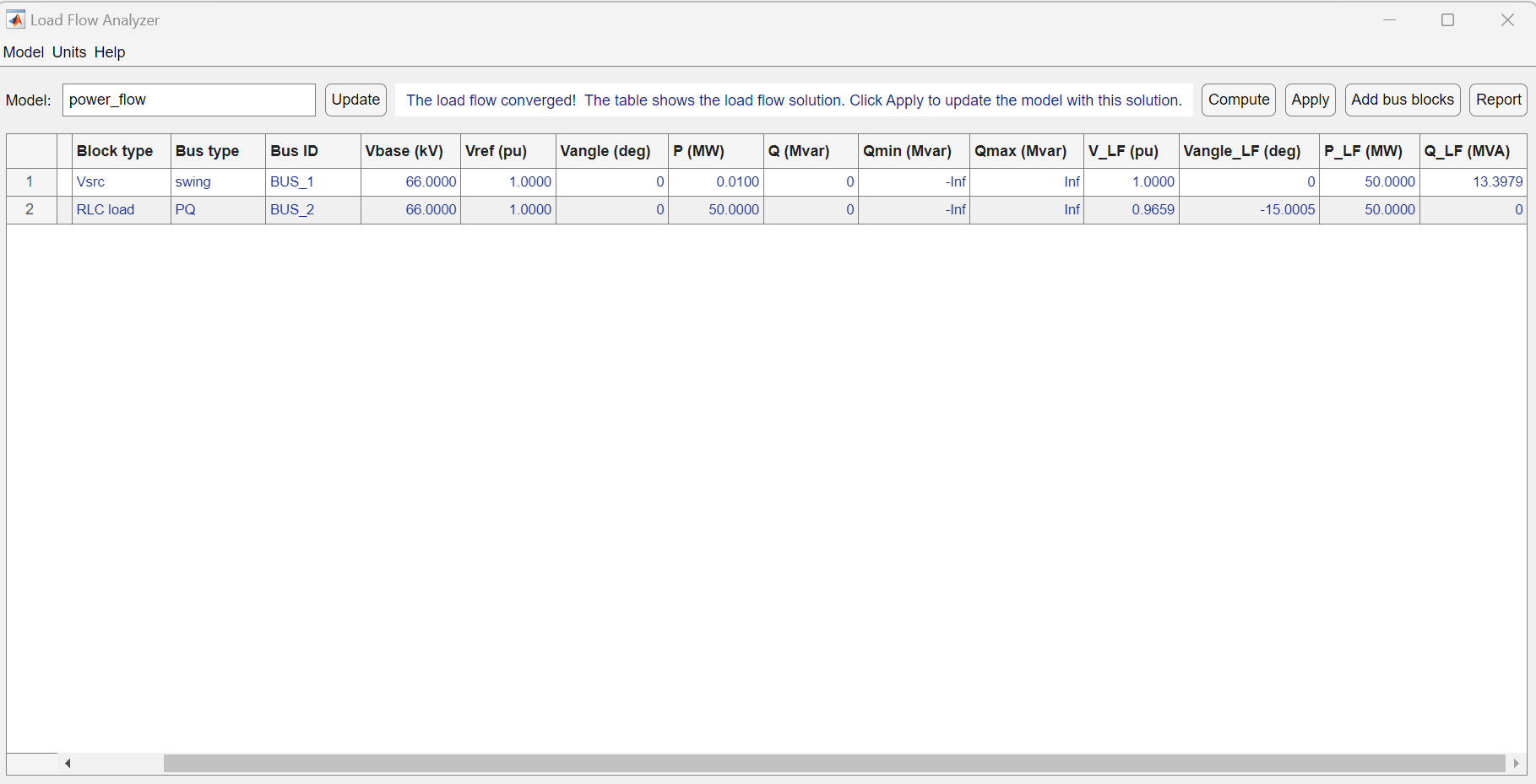
Commputeを実行した結果を図7に示します。潮流計算結果を表3のとおり整理します。本シミュレーションでは電圧位相が送電端基準になっています。また、受電端電圧と相差角について、MATLAB/Simulinkで計算結果が、先ほどの計算結果とほぼ一致していることがわかるかと思います。若干の誤差が発生していますが、この原因については私はよくわかっていません。有識者がいましたら、教えてください。
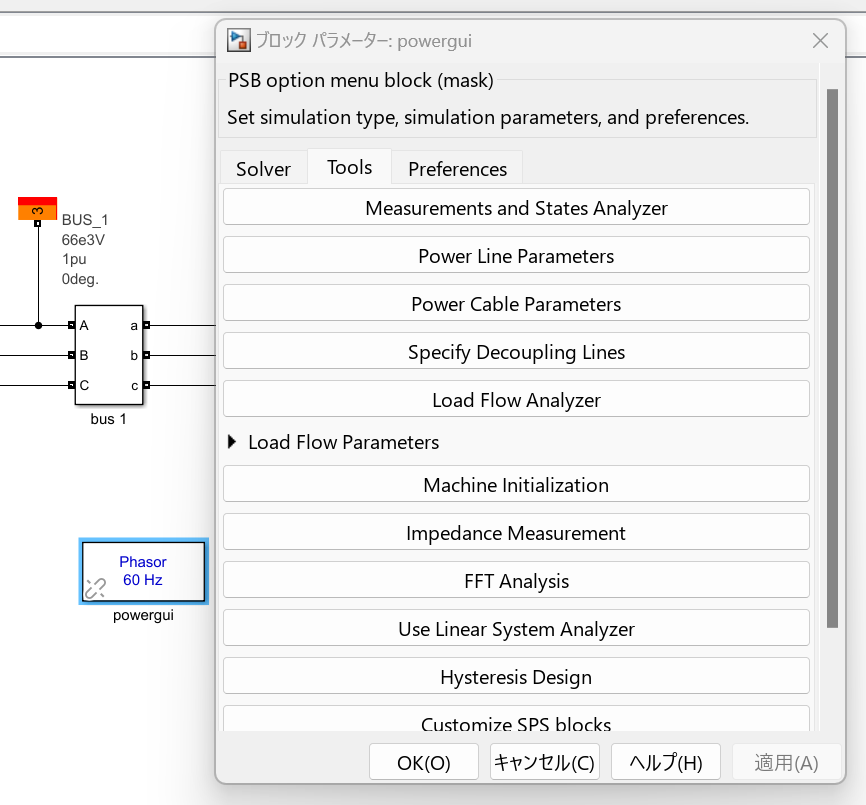
図5 Power GuiからLoad Flow Analyzerを呼び出す。
図6 Load Flow Analyzer の画面
図7 潮流計算結果
表3 潮流計算結果の整理
| 送電端 | 受電端 | |
|---|---|---|
| 電圧 pu | 1.0000 | 0.9659⇒一致 |
| 電圧位相 deg | 0 | -15.0005⇒一致 |
| 有効電力 MW | 50 | 50 |
| 無効電力 Mvar | 13.3979 | 0 |
まとめ
本記事では、電力系統の潮流計算をしてみました。電気回路的な解とMATLAB/Simulinkによる解が無事一致したことを確認しました。私見ですが、潮流計算をしてみようと思っても、簡単にできる資料がないと感じています。本記事を参考に、実装してみていただければと思います。
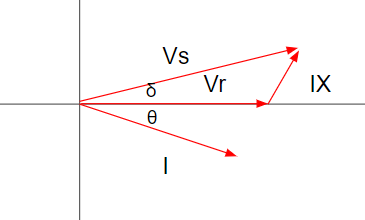
（参考）フェーザ図
この項目も書いてしまったので、残しておきます。
ベクトル図として、送電端電圧、受電端電圧、電流、力率、相差角などの関係性を表したものが以下の図8になります。実数軸と虚数軸について方程式を立てることで、よって以下の式を得ることができます。
実数軸 $V_s \cos{\delta} = V_r + IX\sin{\theta}$
虚数軸 $V_s \sinδ = IX\cos{\theta}$
図8 送電端と受電端のフェーザ図