はじめまして。Blitz1127です。
MATLAB/Simscape Electricalで電気回路をいじろうということで、メジャーなRLC直列回路を解析していこうと思います。
対象とする回路
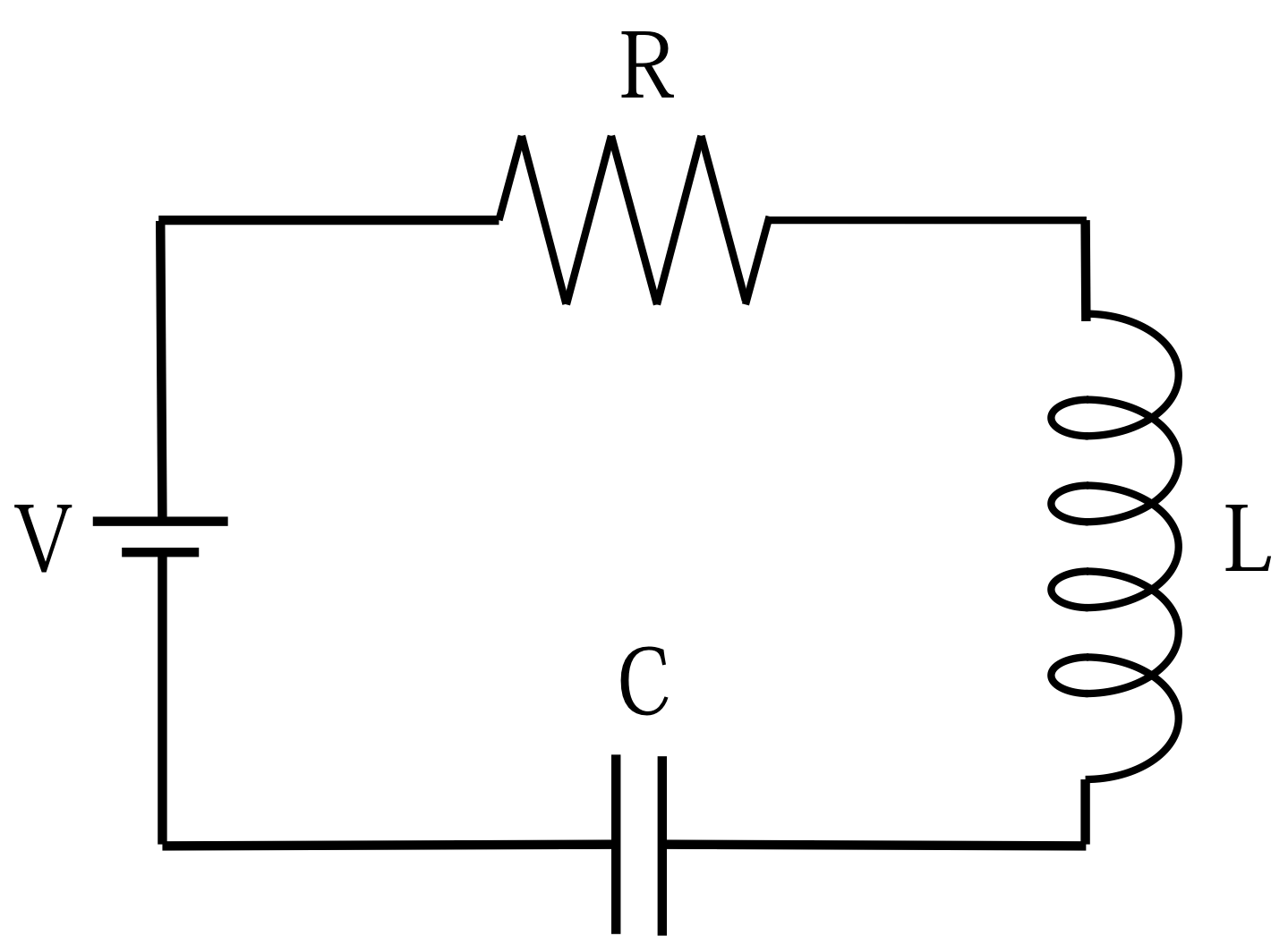
対象は図1のような、RLC直列回路とします。初期充電や初期電流がない状態でこのような回路が形成されたとします。
図1 RLC直列回路の例
電気回路理論による電流過渡応答の算出
RLC直列回路について、キルヒホッフの電圧則を使います。まずは、各回路素子の電圧を算出します。電源電圧$V_{source}$、抵抗電圧$V_r$、インダクタ電圧$V_l$、キャパシタ電圧$V_c$は以下のとおりです。
$V_{source}$=$V_{dc}$
$V_r(t)=RI(t)$
$V_l(t)=L\frac{dI(t)}{dt}$
$V_c(t)=\frac{Q(t)}{C}=\frac{\int{Itdt}}{C}$
従って、キルヒホッフの法則(電圧ループ則)を考えると以下の式になります。
$V_{source}=V_r+V_c+V_l$
$V_{dc}=RI(t)+\frac{\int{I(t)dt}}{C}+L \frac{dI(t)}{dt}$
この式をtについて微分することにより、次の微分方程式を得ることができます。
$L \frac{d^2I(t)}{dt^2}+R\frac{dI(t)}{dt}+\frac{I(t)}{C}=0$
この2階の微分方程式について、ラプラス変換をすると次の式になります。
$s^2+\frac{R}{L}s+\frac{1}{LC}=0$
ここで、判別式Dを用います。
$D = (\frac{R}{L})^2-\frac{4}{LC}$
この判別式を利用することで、3種類のパターンに判別することができます。
1)$(\frac{R}{2L})^2-\frac{1}{LC}>0$のとき、過制動となります。
このときの電流は、初期条件も考慮すると次の式で表せます。
$ I(t)=\frac{Vdc}{2L\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}} e^{(-\frac{R}{2L}+\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}})t}-\frac{Vdc}{2L\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}}} e^{(-\frac{R}{2L}-\sqrt{(\frac{R}{2L})^2-\frac{1}{LC}})t}$
2)$(\frac{R}{2L})^2-\frac{1}{LC}=0$のとき、臨界制動となります。
このときの電流は、初期条件も考慮すると次の式で表せます。
$I(t)=\frac{V_{dc}}{L} e^{-\frac{R}{2L}t}t$
3)$(\frac{R}{2L})^2-\frac{1}{LC}<0$のとき、減衰振動となります。
このときの電流は、初期条件も考慮すると次の式で表せます。
$I(t)=\frac{Vdc}{\frac{1}{LC} -(\frac{R}{2L})^2}e^{-\frac{R}{2L}t}\sin{(\frac{1}{LC} -(\frac{R}{2L})^2)t}$
MATLAB/Simscape Electricalを用いた解析モデル
先ほどは電気回路理論から微分方程式を算出し、その解から波形を得るということを実施しました。この手法は理論的であり、誤りがありません。しかしながら、より回路が複雑になった場合に、同様な手法で解が求められるでしょうか?例えば、LEDのような非線形素子が回路にあった場合、先程のような解き方で解を得られるとは限りません。そこで、MATLAB/Simscape Electricalのようなシミュレーションが役に立ってきます。
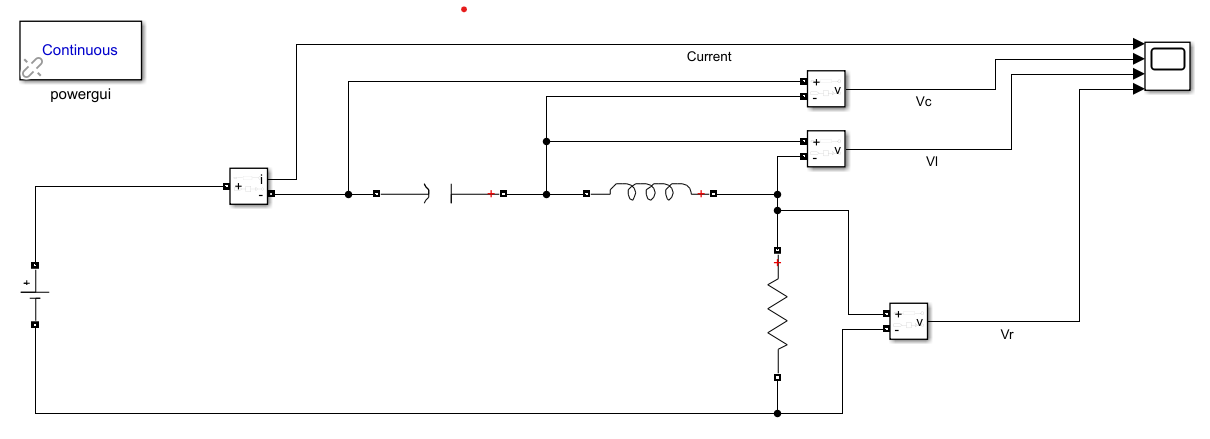
MATLAB/Simscape Electricalでのモデルを図2のとおりとします。RLCを直列に接続します。回路のパラメータとしては、表1のとおり与えます。
図2 RLC直列回路のMATLAB/Simscape Electricalモデル
表1 回路パラメータリスト
| 条件 | 過制動 | 臨界制動 | 減衰振動 |
|---|---|---|---|
| 電源電圧 | 1V | 1V | 1V |
| キャパシタ | 1uF | 1uF | 1uF |
| インダクタ | 1mH | 1mH | 1mH |
| 抵抗 | 300Ω | 63.24555Ω | 10Ω |
注意)数値シミュレーションは計算時間を指定することができます。一方、世の中にはサンプリング定理なるものが存在しており、波形の2倍の周波数以上の周波数で測定を行わなければ正しく測定できません、そのため、シミュレーションのサンプリング時間は波形の振動速度を考慮したうえで設定する必要が出てきます。
MATLAB/Simscape Electricalを用いた計算結果と理論式の計算結果の比較
モデルの構築もできたので、MATLAB/Simscape Electricalを用いた計算結果と理論式から計算した計算結果を比較しましょう。
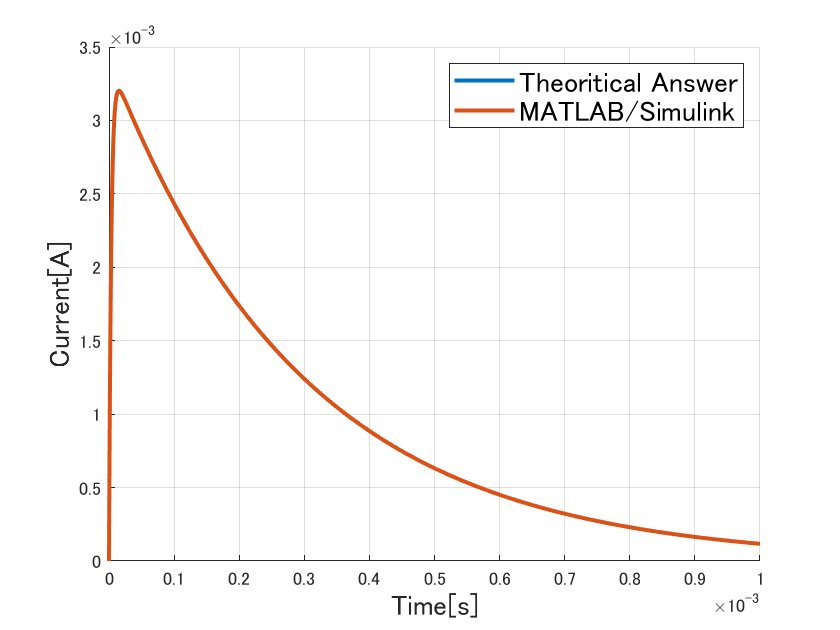
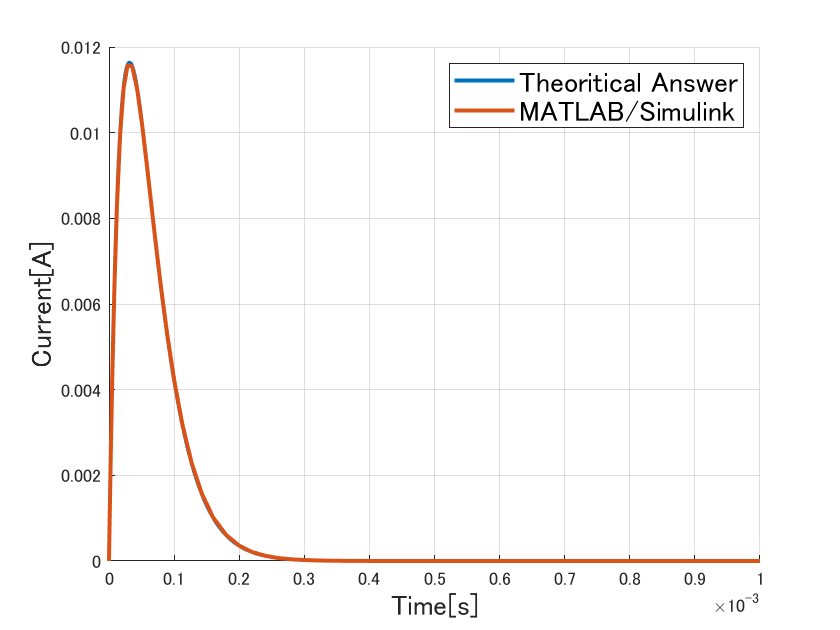
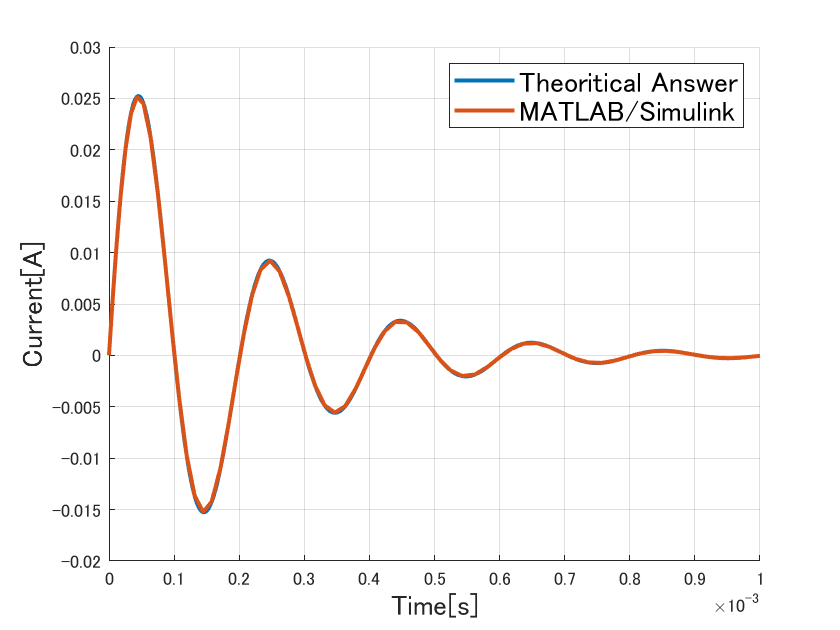
図3~5が比較した計算結果になっています。青線が理論式から計算した結果を、朱線がMATLAB/Simscape Electricalを用いた計算結果を示しています。2つの計算方法で計算結果が一致していることがわかります。なお、ピーク値付近で多少のズレがありますが、サンプリング点数の問題です。より詳細に解析を行えば、MATLAB/Simscape Electricalの値は理論式の計算結果と一致していきます。
図3 過制動時の解析結果比較
図5 減衰振動時の解析結果比較
まとめ
本記事ではRLC直列回路を用いて、理論式とMATLAB/Simscape Electricalの計算結果を比較しました。RLC直列回路は電気系の学生やエンジニアであれば見たことがある回路かと思います。初記事ということもあり、誰もが知っている回路でのシミュレーションを紹介しました。
理論式は、回路が複雑になっていくと計算が困難になるという課題がありますが、MATLAB/Simulinkの解析はそのような課題がありません。MATLAB/Simulinkは楽しいので、どんどん触っていきたいです。