はじめに
乱数を発生させて円周率を計算できるというのを知っていましたが、初めて実装しました。新規性も何もないですが、matlabでの実装法を知りたい人は御覧ください。
円周率を計算する方法
まず、どのように円周率を計算するか説明します。
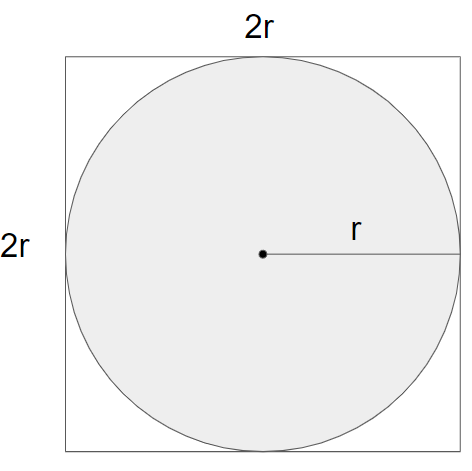
ある正方形に円が内接している場合を考えます。円の面積は次のとおりです
S_{circle} = \pi r^2
次に正方形の面積は次のとおりです。
S_{square} = 4 \times r^2
したがって、正方形における円の面積比率は次のとおりです。
S_{rate} = S_{circle} / S_{square} = \pi/4
つまり、正方形型の乱数を発生させ、円の中に入る確率が$\pi/4$となります。
実装
それでは、matlabを使用して円周率を計算します。
今回は乱数を-1~1で発生させます。内接する円は(0,0)を中心とした半径1の円です。
正方形の乱数を発生させる
まずは正方形の乱数を100個発生させます。
N = 100
x = 2*rand(N,1)-1;
y = 2*rand(N,1)-1;
円を定義し、確認する
この項目は必須ではないですが、円を定義し、乱数との関係を整理します。
cx = 0; cy = 0; % 中心
r = 1; % 半径
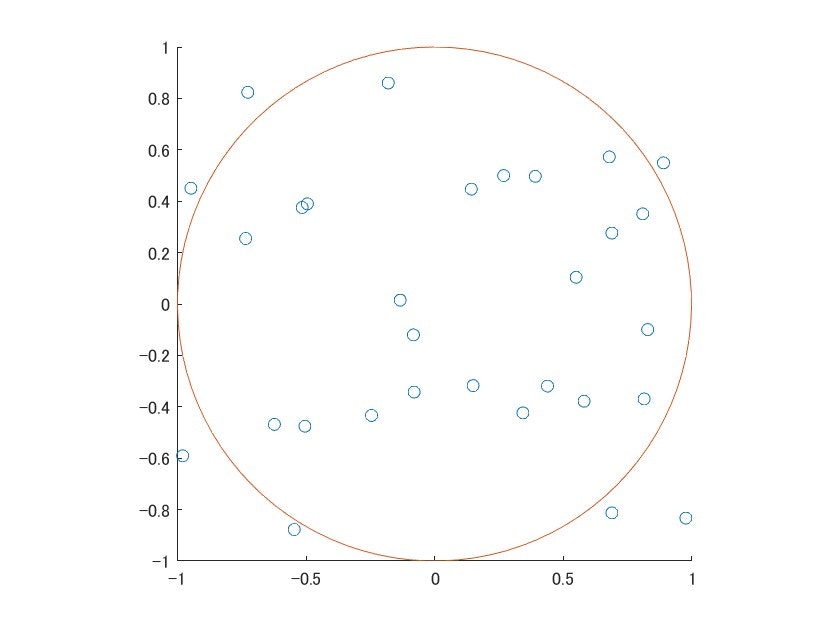
hold on
scatter(x(1:30),y(1:30));
t = linspace(0,2*pi,100);
plot(r*sin(t)+cx,r*cos(t)+cy)
axis square
このコードを実行すると次のような図が出てきます。乱数が円の中に入っていたり入っていなかったりします。
円に入っているか判別し、数を数える
円の中心からの距離を求め、その距離が半径より小さい場合は円の中に入っていると考えます。
dist = sqrt((x-cx).^2 + (y-cy).^2);
n = length(find(dist<r));
円の中に入っている数を計算し、円周率を求める
ここまでで、円の中に入っている乱数の数がわかりました。
ここから、円周率を求めます。
calc_pi = n/N * 4
結果
計算したところ次のようになりました。
N=100のとき3.52
N=1000のとき3.156
N=10000のとき3.13
N=100000のとき3.1427
このように乱数の数が増えていくにつれて真の値(3.1415…)に近づくことがわかりました。なお、乱数ですので、上記値は演算を行うたびに変わります。この値がどのような散らばりを持つかなどは統計学を学ぶ必要があります。
感想
初めて乱数を用いた計算をしてみました。乱数はこのようにとにかく数をこなしてみるという活用がありそうです。つまり、平均がどこに収束するか、乱数によりどれくらい値がばらつくかなどを評価できそうです。