※ 2022年2月27日 回転行列の誤植を修正しました.
はじめに
最近趣味のロボットで順運動学を求めるのにDH法を使ってみたのですが,授業で昔教わったきりの曖昧な理解と記憶と思い込みで計算していたところ大ハマリしました.具体的には,「線形代数で習ったベクトルの回転行列みたいにどんどん左にかけていけばいいんだろ」をやり,一向に計算が合わないなどしました.そこで,同次変換行列について勉強し直した内容を基に,なぜ左にかけていかないのか定性的な解釈を書き添えながらまとめていきます.
本稿では,まず僕のしていた思い込みの内容を通じて2次元平面上で列ベクトルに作用させる回転行列とその性質を示し,それを拡張する形で列ベクトルに作用させる同次変換行列を求めます.その後,2つの座標系の関係を表現するために,同時変換行列を座標系に作用させた場合について述べます.これらを対比させることで,なぜDH法の同次変換行列は左にかけていかないのかを解釈していきます.
理詰めから定性的な解釈を得ようとしたところ,思ったよりボリュームが大きくなってしまいました.DH法や座標系間の同次変換行列だけでなく,線形代数で習うようなベクトル(が指し示す点)に対する同次変換についての内容を知りたい方にも是非読んで頂きたい内容です.
端的な結論
この先長々と行列の話をするのですが,読み進める前に結論を知りたい!という方のために端的に述べておきます.二言でまとめると「同次変換行列をベクトルに作用させて点を移すことと,同次変換行列を座標系間の関係を表すのに用いることは別物なので同じ性質とは限らないから」,「行列の掛け算の定義上,左から掛けると『回転と並進は変換を作用させられる側の座標系を基準とする』というルールを満たせないから」ということになります.同じような行列演算なのですが,その解釈の仕方が異なるのです.何がどう違うのか,そのルールはどこから来たのか,という話をこの先で述べます.
どんな思い込みをしていたか
「変換行列の掛け算で連続した座標変換を表せる」ということだけ覚えていた僕は,真っ先に回転行列を思い出しました.

この図において,回転行列には次のような関係が成り立ちます.
\begin{align}
\boldsymbol{p}_2 &= \boldsymbol{R}(\theta_1)\boldsymbol{p}_{1} \\
\boldsymbol{p}_3 &= \boldsymbol{R}(\theta_2)\boldsymbol{p}_{2} \\
&= \boldsymbol{R}(\theta_2)\boldsymbol{R}(\theta_1)\boldsymbol{p}_{1}
\end{align}\\
ただし,$\boldsymbol{R}(\theta)$は回転行列でその中身は
\boldsymbol{R}(\theta) =
\begin{bmatrix}
\cos(\theta) & -\sin(\theta) \\
\sin(\theta) & \cos(\theta) \\
\end{bmatrix}
です.
実際に計算してみると,
\begin{align}
p_2 &=
\begin{bmatrix}
\cos(\pi/2) & -\sin(\pi/2) \\
\sin(\pi/2) & \cos(\pi/2) \\
\end{bmatrix}
\begin{bmatrix}
3\\
0\\
\end{bmatrix}\\
&=
\begin{bmatrix}
\frac{1}{\sqrt2} & -\frac{1}{\sqrt2} \\
\frac{1}{\sqrt2} & \frac{1}{\sqrt2} \\
\end{bmatrix}
\begin{bmatrix}
3\\
0\\
\end{bmatrix}\\
&=
\begin{bmatrix}
\frac{3\sqrt2}{2} \\
\frac{3\sqrt2}{2}\\
\end{bmatrix}\\
p_3 &=
\begin{bmatrix}
\cos(\pi/2) & -\sin(\pi/2) \\
\sin(\pi/2) & \cos(\pi/2) \\
\end{bmatrix}
\begin{bmatrix}
\frac{3\sqrt2}{2} \\
\frac{3\sqrt2}{2}\\
\end{bmatrix}\\
&=
\begin{bmatrix}
0 \\
3\\
\end{bmatrix}\\
\end{align}
ちゃんと図の通りになりますね.要するに何が言いたいかというと,
「列ベクトル$\boldsymbol{p_1}$に対し連続して作用させる回転変換$\boldsymbol{R}(\theta_1), \boldsymbol{R}(\theta_2)$は,$\boldsymbol{p}_3 = \boldsymbol{R}(\theta_2)\boldsymbol{R}(\theta_1)\boldsymbol{p_1}$のように変換行列を『左から』次々に乗じていくことで計算できる」
ということです.
僕はこの性質が座標系間の関係を表す同次変換行列でも同じように適用される(同次変換$\boldsymbol{T}$も左からかけていけば良いんだ!)と思い込んでしまいました.思い込んでいた,というからには実際にはそうではなく,これが諸悪の根源だったわけです.
僕のぽんこつを具体的に示したところで,次節から「同次変換行列とはそもそも何か」という話を基に,なぜ同じ性質にはならないのかを考えていきます.
列ベクトルに作用させる同次変換行列
そもそも同次変換行列とは
さて,前節ではベクトルの回転を行列の掛け算で表現できるという計算を示したわけですが,こうなると「回転が表現できるなら並進も扱いたい」と思い始めます.人間は強欲な生き物で,更に贅沢を言って「でも掛け算と足し算が両方出てくるのは扱いが悪い.回転から並進まで含めて一個の行列を乗じるだけで表現したい」と言い始めます.このモチベーションから生まれた変換こそ同次変換行列です.
2次元平面における同次変換行列を求める
いきなり3次元で話をすると非常に難しくなるので,前節の話を拡張して次図のような2次元平面での回転・並進を考えてみます.
 前節の問題では2個目の変換が$\theta_2$に関する回転だったものを,$y$方向に$+2$並進するという変換に置き換えました.列ベクトルの回転と並進を考えるとき,次の関係が成り立ちます.
前節の問題では2個目の変換が$\theta_2$に関する回転だったものを,$y$方向に$+2$並進するという変換に置き換えました.列ベクトルの回転と並進を考えるとき,次の関係が成り立ちます.
\begin{align}
\boldsymbol{p}_2 &= \boldsymbol{R}(\theta_1)\boldsymbol{p}_{1} \\
\boldsymbol{p}_3 &= \boldsymbol{p}_{2} + \boldsymbol{r}_{\rm shift}\\
&= \boldsymbol{R}(\theta_1)\boldsymbol{p_1} + \boldsymbol{r}_{\rm shift}
\end{align}\\
ただし,
\begin{align}
\boldsymbol{R}(\theta) &=
\begin{bmatrix}
\cos(\theta) & -\sin(\theta) \\
\sin(\theta) & \cos(\theta) \\
\end{bmatrix}\\
\boldsymbol{r}_{\rm shift} &=
\begin{bmatrix}
x_{\rm shift} \\
y_{\rm shift} \\
\end{bmatrix}
\end{align}
です.$\boldsymbol r_{\rm shift}$は並進を表す列ベクトルで,図の例では$\boldsymbol r_{\rm shift}=[0 2]^T$ということになります.$\boldsymbol{R} (\theta)$は前と同様に回転行列です.
実際に計算してみると,
\begin{align}
p_2 &=
\begin{bmatrix}
\cos(\pi/2) & -\sin(\pi/2) \\
\sin(\pi/2) & \cos(\pi/2) \\
\end{bmatrix}
\begin{bmatrix}
3\\
0\\
\end{bmatrix}\\
&=
\begin{bmatrix}
\frac{1}{\sqrt2} & -\frac{1}{\sqrt2} \\
\frac{1}{\sqrt2} & \frac{1}{\sqrt2} \\
\end{bmatrix}
\begin{bmatrix}
3\\
0\\
\end{bmatrix}\\
&=
\begin{bmatrix}
\frac{3\sqrt2}{2} \\
\frac{3\sqrt2}{2}\\
\end{bmatrix}\\
p_3 &=
\begin{bmatrix}
\frac{3\sqrt2}{2} \\
\frac{3\sqrt2}{2}\\
\end{bmatrix}
+
\begin{bmatrix}
0 \\
2\\
\end{bmatrix}\\
&=
\begin{bmatrix}
\frac{3\sqrt2}{2} \\
\frac{3\sqrt2}{2} + 2\\
\end{bmatrix}
\end{align}
はい.ちゃんと図と一緒になりました.
ここから先程述べた「並進も乗算一回にまとめたい」を実現するために,$+\boldsymbol r_{\rm shift}$の項をどうにか掛け算の中に収めます.行列の掛け算をするときは,要素同士を乗じたものを(左の行列の行方向に)足し上げるじゃないか,ということを上手く利用するとなんと乗算一個に書き換えられるのです.
まず,変換前の列ベクトル$\boldsymbol{p}$,変換後の列ベクトル$\boldsymbol{p}'$,回転行列$\boldsymbol{R}(\theta)$,並進成分の列ベクトル$\boldsymbol{r}_{\rm shift}$の中身を次式のように定めます.
\begin{align}
\boldsymbol{p} &=
\begin{bmatrix}
p_x\\
p_y\\
\end{bmatrix}\\
\boldsymbol{p}' &=
\begin{bmatrix}
p'_x\\
p'_y\\
\end{bmatrix}\\
\boldsymbol{R}(\theta) &=
\begin{bmatrix}
\cos(\theta) & -\sin(\theta) \\
\sin(\theta) & \cos(\theta) \\
\end{bmatrix}\\
\boldsymbol{r}_{\rm shift} &=
\begin{bmatrix}
x_{\rm shift} \\
y_{\rm shift} \\
\end{bmatrix}
\end{align}
これらを用いて,「$\boldsymbol{p}$をその場で回転させ,それを$\boldsymbol{r}_{\rm shift}$だけ並進させたものを$\boldsymbol{p}'$とする」という一連の変換を表すと,
\begin{align}
\boldsymbol{p}' &= \boldsymbol{R}(\theta)\boldsymbol{p} + \boldsymbol{r}_{\rm shift} \\
\begin{bmatrix}
p'_x\\
p'_y\\
\end{bmatrix}
&=
\begin{bmatrix}
\cos(\theta) & -\sin(\theta) \\
\sin(\theta) & \cos(\theta) \\
\end{bmatrix}
\begin{bmatrix}
p_x\\
p_y\\
\end{bmatrix}
+
\begin{bmatrix}
x_{\rm shift} \\
y_{\rm shift} \\
\end{bmatrix}\\
&=
\begin{bmatrix}
\cos(\theta) p_x -\sin(\theta) p_y \\
\sin(\theta) p_x +\cos(\theta) p_y\\
\end{bmatrix}
+
\begin{bmatrix}
x_{\rm shift} \\
y_{\rm shift} \\
\end{bmatrix}\\
&=
\begin{bmatrix}
\cos(\theta) p_x -\sin(\theta) p_y + x_{\rm shift} \\
\sin(\theta) p_x +\cos(\theta) p_y + y_{\rm shift} \\
\end{bmatrix}
\end{align}
となります.ここまでは代入と掛け算と足し算なので普通ですが,ここで一工夫加えて次のように書き換えます.
\begin{align}
\begin{bmatrix}
p'_x\\
p'_y\\
1 \\
\end{bmatrix}
&=
\begin{bmatrix}
\cos(\theta) p_x -\sin(\theta) p_y + x_{\rm shift} \\
\sin(\theta) p_x +\cos(\theta) p_y + y_{\rm shift} \\
0 + 0 + 1
\end{bmatrix}
\end{align}
両辺の一番下の行に$1$と$0$を無理やり付け加えました.これの何が嬉しいかといえば,こうすることで次のように一回の乗算へ変形できるのです!!
\begin{align}
\begin{bmatrix}
p'_x\\
p'_y\\
1 \\
\end{bmatrix}
&=
\begin{bmatrix}
\cos(\theta) p_x -\sin(\theta) p_y + x_{\rm shift} \\
\sin(\theta) p_x +\cos(\theta) p_y + y_{\rm shift} \\
0 + 0 + 1
\end{bmatrix}\\
&=
\begin{bmatrix}
\cos(\theta) \cdot p_x -\sin(\theta) \cdot p_y + x_{\rm shift} \cdot 1 \\
\sin(\theta) \cdot p_x +\cos(\theta) \cdot p_y + y_{\rm shift} \cdot 1 \\
0 \cdot p_x + 0 \cdot p_y + 1 \cdot 1
\end{bmatrix}\\
&=
\begin{bmatrix}
\cos(\theta) & -\sin(\theta) & x_{\rm shift} \\
\sin(\theta) & \cos(\theta) & y_{\rm shift} \\
0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
p_x \\
p_y \\
1
\end{bmatrix}\\
\end{align}
はい.「回転と並進の要素からできる行列」と「変換前のベクトルからできる列ベクトル」を一回掛け算するだけで,回転と並進を含む変換を列ベクトルへ一気に作用させられるようになりました.この$3\times3$の行列こそが同次変換行列なのです!余談ですが,この同次変換行列は3次元空間で考えると$4\times4$の行列になります.
座標系に作用させる同次変換行列
さて,前節で無事に同次変換行列を求められたわけですが,あそこで考えていた問題は「列ベクトル(が指し示す点)を回転・並進移動させる」ことでした.しかし,マニピュレータやロボットの脚を制御する際に考えたいのは***「各関節に定めた座標系同士の関係はどのように表現できるか」***ということです.別に列ベクトルをくるくる回したいわけではありません.そこで本節では,同次変換行列を「座標系$\Sigma_0$から座標系$\Sigma_1$への変換に用いたらどうなるのか」という内容について考えます.
はじめにや節タイトルで「列ベクトルに作用させる同次変換行列」「座標系に作用させる同次変換行列」と,さも別物のように扱っていますが行列自体は同じものです.想定している使い方が違うから定性的な解釈も変わってくるはずだよね,くらいの感覚で区別しています.
2次元平面上の座標系に同次変換を作用させてみる
まず,前節で行った回転・並進を座標系に作用させることを考えます.
前節では列ベクトルを,
- 原点を中心に$\pi/4$ rad回す.
- $y$軸方向に$+2$並進させる.
という処理を行い,同次変換行列で表現してみたのでした.本節ではこれを座標系に対して行うのですが,座標系を変換して座標系を作り出すと,2つの座標系が混在し話が難しいことになります.そこで,変換前の座標系を基準座標系$\Sigma_0$,変換後に作られた座標系を$\Sigma_1$と呼ぶことにします.更に,どちらの座標系に基づいて回転や移動を行っているのかを明確にするために,2つの処理を次のように書き改めます.
- 基準座標系$\Sigma_0$の原点を中心に,$\pi/4$ rad回転する
- 1.で回転させたものを,基準座標系$\Sigma_0$の$y$軸に沿って$+2$並進させた座標系を$\Sigma_1$とする.
どうでしょう.何やら細かい表現が増えましたが,主張している内容は以前と全く一緒です.文字だけで書くとわかりにくいので図で描いてみます.

文字だけよりもかなり分かりやすくなってのではないでしょうか.この図のポイントは,回転も並進も基準座標系$\Sigma_0$に対して行われているところです.すなわち,「変換を作用させられた側の座標系を基準として,回転と並進が計算される」ということになります.このポイントが次節で述べる比較において重要になってきます.
右からかけたものと左からかけたものを比べる
本節では2つの同次変換行列$\boldsymbol T_1, \boldsymbol T_2$を用意して,$\boldsymbol T_1$に対して$\boldsymbol T_2$を右からかけたものと左からかけたものを比較してみます.この比較を通じて,「変換を作用させられた側の座標系を基準として,回転と並進が計算される」というポイントを満たすには左右どちらからかけるべきなのかを確認していきます.
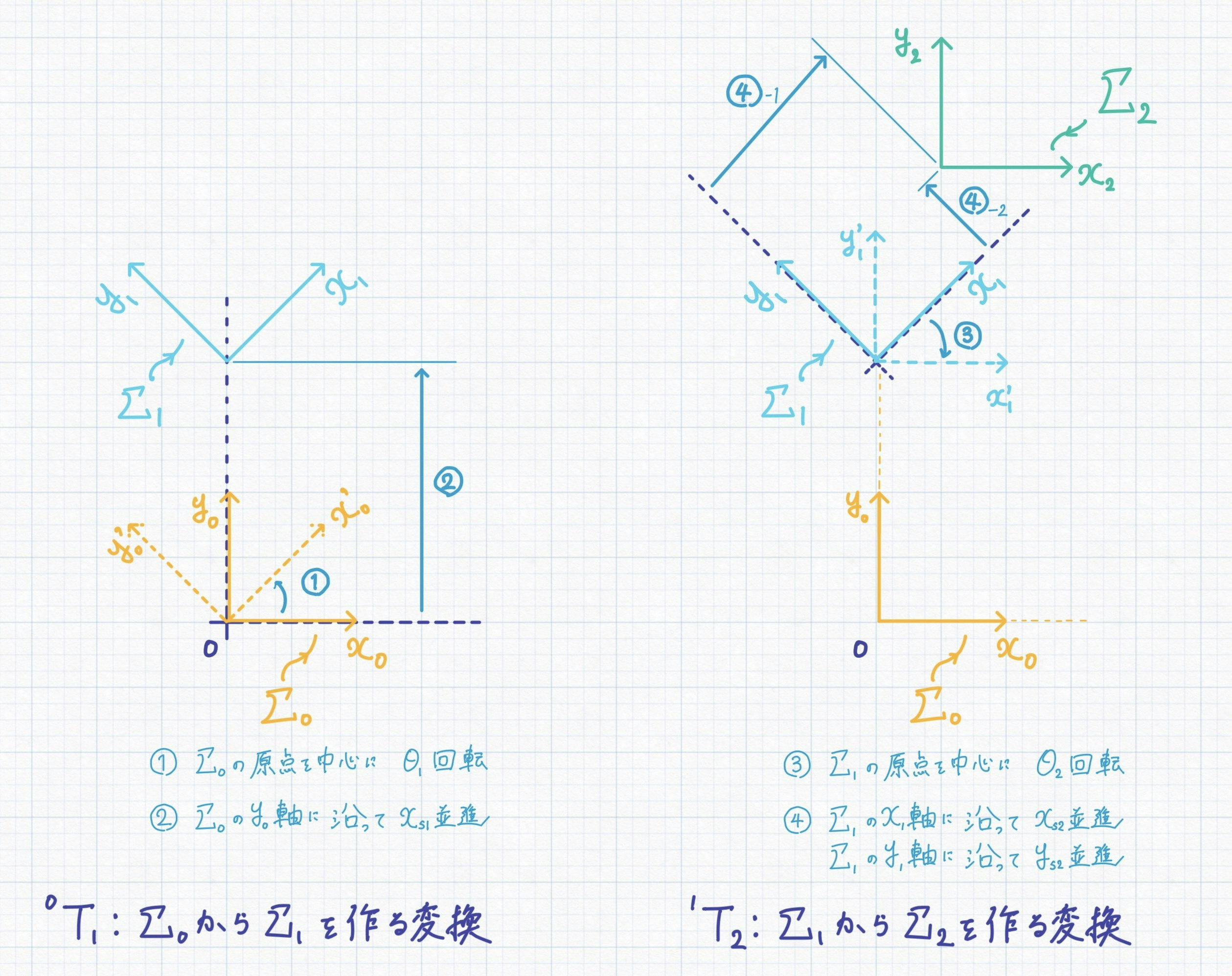
ここでは,基準座標系$\Sigma_0$に対して2つの同次変換行列$\boldsymbol T_1, \boldsymbol T_2$を順番に作用させていくことを考えます.すなわち,ここで行いたい操作は,
- $\Sigma_0$に$\boldsymbol T_1$を作用させて$\Sigma_1$を作る.
- $\Sigma_1$に$\boldsymbol T_2$を作用させて$\Sigma_2$を作る.
この図では1個目の同次変換で$y$方向にしか並進しなかったり,1個目と2個目の回転を逆向きにしたりしていますが,作図を楽にするためにそうしているだけであり,特別な意味はありません.厳密な証明は省きますが,当然このような制約がなくても「左右どちらからかけるか」という問題の結論は変わりません.
先に結論を述べると,左からかけたものは「変換を作用させられた側の座標系を基準として,回転と並進が計算される」という操作を実現できません.
何が起きるのかというと,本来このような連続した変換を考えるとき$\boldsymbol T_2$による回転と移動は,変換を「作用させられた側の座標系」である$\Sigma_1$を基準とした操作にならなくてはいけません.しかし$\boldsymbol T_2$を$\boldsymbol T_1$に左からかけると,$\boldsymbol T_2$の並進成分が$\Sigma_0$を基準に計算されてしまうのです.これがなぜ起きるか,まで突き詰めると「行列の掛け算の定義上そのような式が表れてしまう」としか言えないのですが,どんな式が表れるのか実際に見てみましょう.
まずは$\boldsymbol T_1, \boldsymbol T_2$をこのように定めます.添字のshiftは長くて見づらいのでsに略しました.
\begin{align}
\boldsymbol T_1
&=
\begin{bmatrix}
\cos(\theta_1) & -\sin(\theta_1) & x_{\rm s1} \\
\sin(\theta_1) & \cos(\theta_1) & y_{\rm s1} \\
0 & 0 & 1\\
\end{bmatrix}\\
\boldsymbol T_2
&=
\begin{bmatrix}
\cos(\theta_2) & -\sin(\theta_2) & x_{\rm s2} \\
\sin(\theta_2) & \cos(\theta_2) & y_{\rm s2} \\
0 & 0 & 1\\
\end{bmatrix}\\
\end{align}
これらをそれぞれ右からと左から掛け合わせると,次式を得ます.
\begin{align}
\boldsymbol T_1 \boldsymbol T_2
&=
\begin{bmatrix}
\cos(\theta_1 + \theta_2) & -\sin(\theta_1 + \theta_2)& 0 & x_{\rm s1} + x_{\rm s2} \cos(\theta_1) - y_{\rm s2} \sin(\theta_1)\\
\sin(\theta_1 + \theta_2) & \cos(\theta_1 + \theta_2) & 0 & y_{\rm s1} + y_{\rm s2} \cos(\theta_1) + x_{\rm s2} \sin(\theta_1)\\
0 & 0 & 1& 0\\
0 & 0 & 0& 1\\
\end{bmatrix}\\
\boldsymbol T_2 \boldsymbol T_1
&=
\begin{bmatrix}
\cos(\theta_1 + \theta_2) & -\sin(\theta_1 + \theta_2)& 0 & x_{\rm s2} + x_{\rm s1} \cos(\theta_2) - y_{\rm s1} \sin(\theta_2)\\
\sin(\theta_1 + \theta2) & \cos(\theta_1 + \theta_2) & 0 & y_{\rm s2} + y_{\rm s1} \cos(\theta_2) + x_{\rm s1} \sin(\theta_2)\\
0 & 0 & 1& 0\\
0 & 0 & 0& 1\\
\end{bmatrix}\\
\end{align}
掛け算の途中計算はあまりに長くて読みにくくなるので省きました.掛け算した直後は両方とも左上の回転行列が加法定理で展開されたような式になります.
これらの式を見てわかるように,回転に関する成分は同じものが表れます.一方で,一番右の行の並進に関する成分は,それぞれ$x_{s1}$と$x_{s2}$を入れ替えたような形になっています.
さて,$\boldsymbol T_1 \boldsymbol T_2$の$x$方向の並進に注目してみましょう.$x_{\rm s1} + x_{\rm s2} \cos(\theta_1) - y_{\rm s2} \sin(\theta_1)$となっています.これは,基準座標系$\Sigma_0$対する$\Sigma_2$の最終的な並進成分が,「$\boldsymbol T_1$が$\Sigma_0$に対して並進する$x_1$と,$\boldsymbol T_2$が$\Sigma_1$に対して持つ並進成分を$\theta_1$を使って$\boldsymbol T_0$基準に直したものの和」であると解釈できます.やはり文字で書くと分かりにくいので,これを図に表してみます.

この図を使って$\Sigma_0$を$\Sigma_2$にするような変換の並進成分を確認してみましょう.$\Sigma_2$の原点を$\Sigma_0$の各軸に射影したもの,すなわち$\Sigma_2$の原点が$\Sigma_0$の座標系においてどこに位置しているのか,を$p_x, p_y$として図に描き入れました.
まず,$x$成分ですが,$\boldsymbol T_1$による並進の$x$成分は0です.そして,$\boldsymbol T_2$による並進の$x$成分は,図から$x_{s2} \cos(\theta_1) - y_{s2} \sin(\theta)$であるとわかります.よって,$p_x$は,
\begin{align}
p_x &= 0 + x_{s2} \cos(\theta_1) - y_{s2} \sin(\theta)\\
&= x_{s2} \cos(\theta_1) - y_{s2} \sin(\theta)
\end{align}
となります.
同様に$y$成分も求めると,
\begin{align}
p_y &= y_{s1} + y_{s2} \cos(\theta) + x_{s1} \sin(\theta_1) \\
\end{align}
はい.$\boldsymbol T_1 \boldsymbol T_2$の並進成分と同じになりました.この図のような順番,すなわち最初に設定した順番で座標系を変換していくためには,右からかけていかないと計算がおかしくなるということが何となく分かったかと思います.図をよく照らすとわかりますが,$x_{s1}, y_{s1}$と$x_{s2}, y_{s2}$が,$\theta_1$と$\theta_2$が入れ替わってしまうことは,変換を作用させる順番が入れ替わるのと同義です.掛け算の順番を入れ替えているので当たり前と言われればそれまでなのですが,行列の中身からも同じことが示せました.
ちなみに$p_x$の式に$x_{s1}$の項がありませんが,これは今回設定した例で$x_{s1}=0$になっているためです.本質とはあまり関係ありません.
おわりに
ここまで,長々と行列計算を交えながら同次変換行列を左に掛けていかない理由を考えました.要点をまとめると,
- 同次変換行列は列ベクトルに対し「原点周りの回転と基準となる座標系に沿った並進を与える」処理であった
- これを座標系に作用させるよう考えると「作用させられる側の座標系を基準に」回転や並進を行うことになる
- 「作用させられる側の座標系を基準に」を行列計算で行おうとすると,行列の積の定義上の都合で右から掛けないといけない.
ということでした.拙い説明を最後までお読み頂きありがとうございました.気になる点や誤りなどがありましたら,是非コメントなどでお知らせください.それでは.