メリークリスマスイブの投稿
Advent Calendar24日目の投稿になります。
https://qiita.com/advent-calendar/2018/quantum2
なぜ、この日なのかということは気にしないでおいてください。
ということで、筆者からのクリスマスプレゼントです。
めり～くりすます！
今回も初心者向けの内容になっています。
Hello Quantumとは
量子コンピューターの操作イメージをスマホ/タブレット上でパズル感覚で遊べるアプリです。
https://helloquantum.mybluemix.net/
この記事を書くにあたって、全ての内容をやりきりましたが、１時間もあれば終わるぐらいの分量なので、気軽に遊んでみてください。
実はIBMが提供しています。IBMは、ついにスマホアプリまで公開するようになったんですね！もっというと、IBM Researchというガチンコの研究所が作成しているようです。
Hello Quantumの画面上での操作
では実際の画面を見てみましょう。
スタート画面
起動するとこんな画面な画面が出てきます。
How to Playを読んでみる
次にHow to Playを眺めてみましょう。チュートリアルのようなものを期待します。
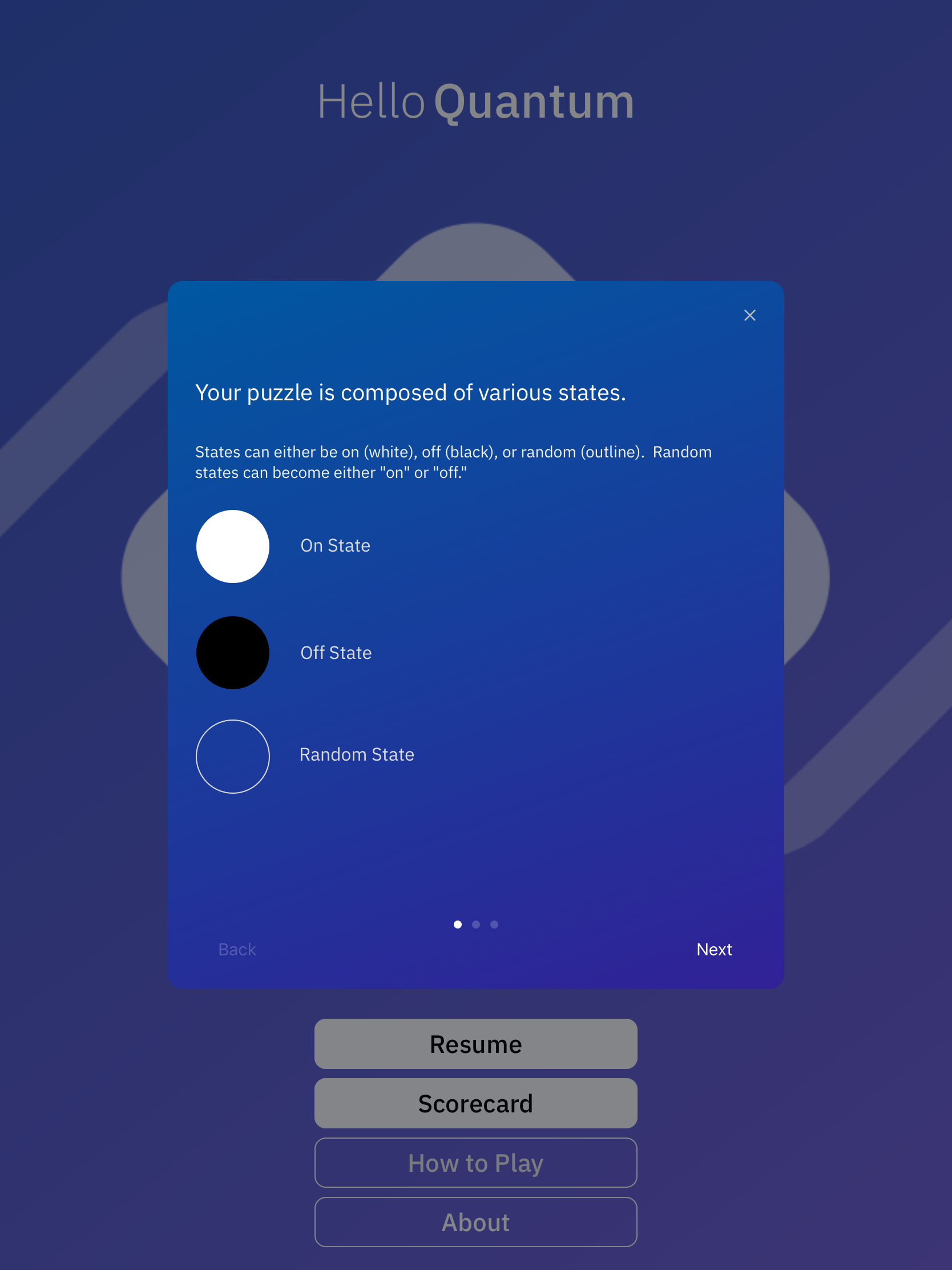
量子状態をオセロのように表現しているようですね。
白がonで|1>、黒がoffが|0>、灰色がramdomなので重ね合わせの状態を表現しているのでしょう。
ここまでは直感的です。
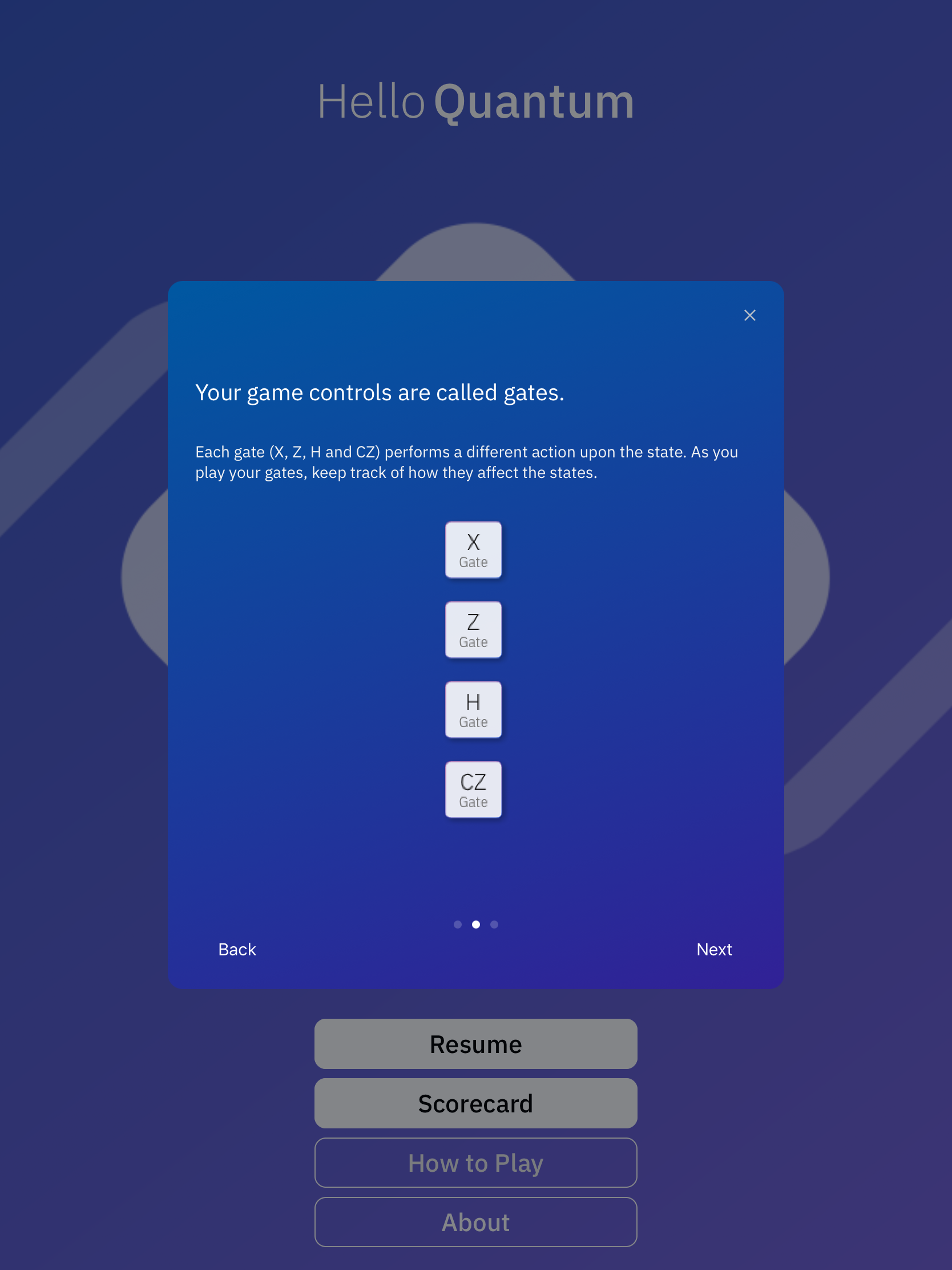ゲートは４種類で、X、Z、H、CZ（Controlled-Z）という、比較的基本的なゲートだけに絞っているようですね。
位相ゲートは表現しづらかったり、初学者にはわかりにくこともあり削ったのかもしれませんね。
これがゲーム画面のようです。それぞれが何を表すかはこれだけではわかりませんが、「target」となる状態に遷移させることがゲームの目的です。
実際のゲーム画面
実際にゲームを始めるとこんな画面が出てきます。
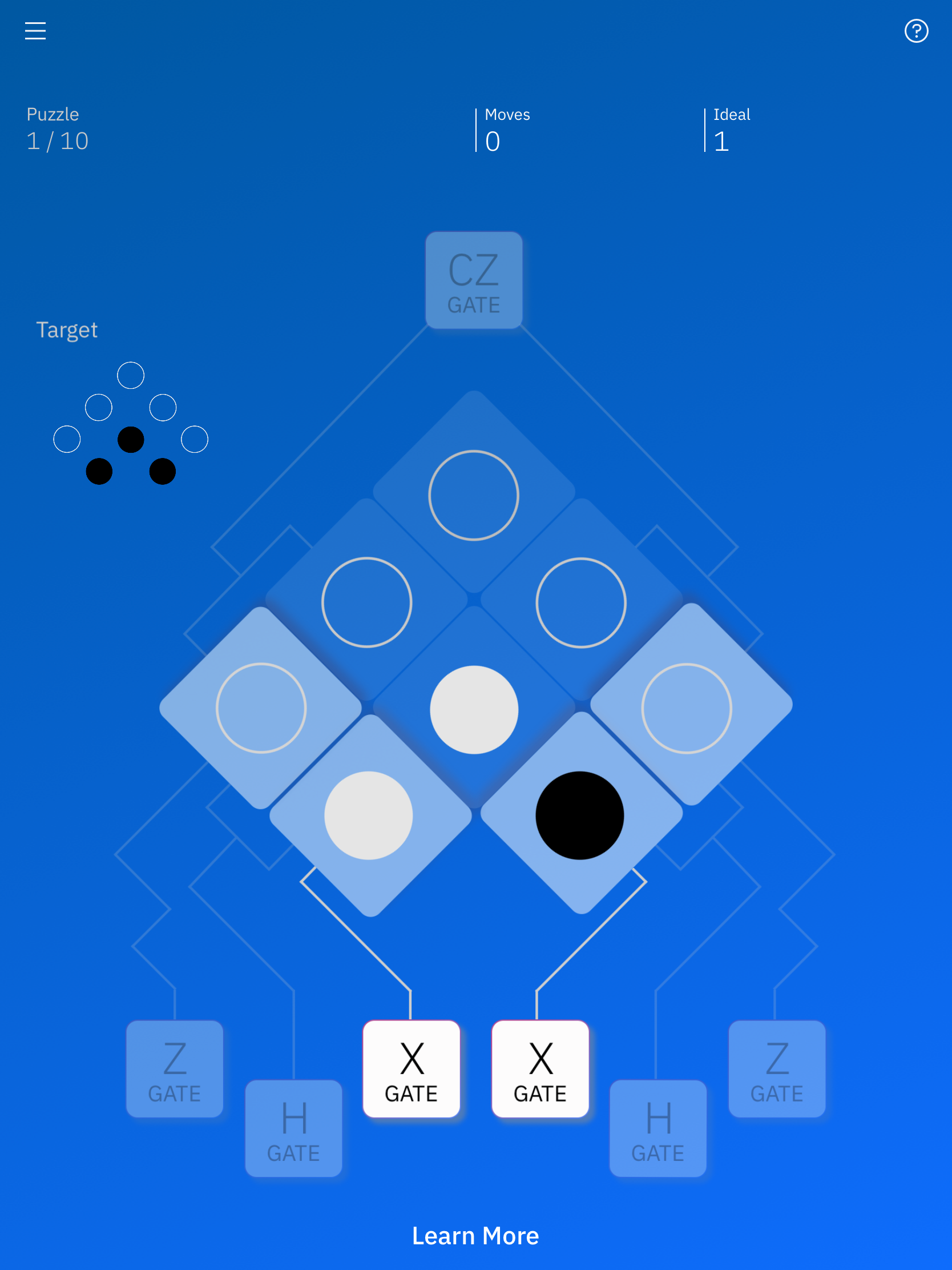
これでやっと見方がわかってきた気がしました。
まず、使えるゲートは限られているようです。この状態ではXゲートだけですね。
では、それをやってみましょう。
Xゲート
Xゲートがon ⇔ offと変換できることを考えると、オセロの白と黒を入れるかだけの操作ということになりますね。
とりあえず、左側のXゲートを押してみます。
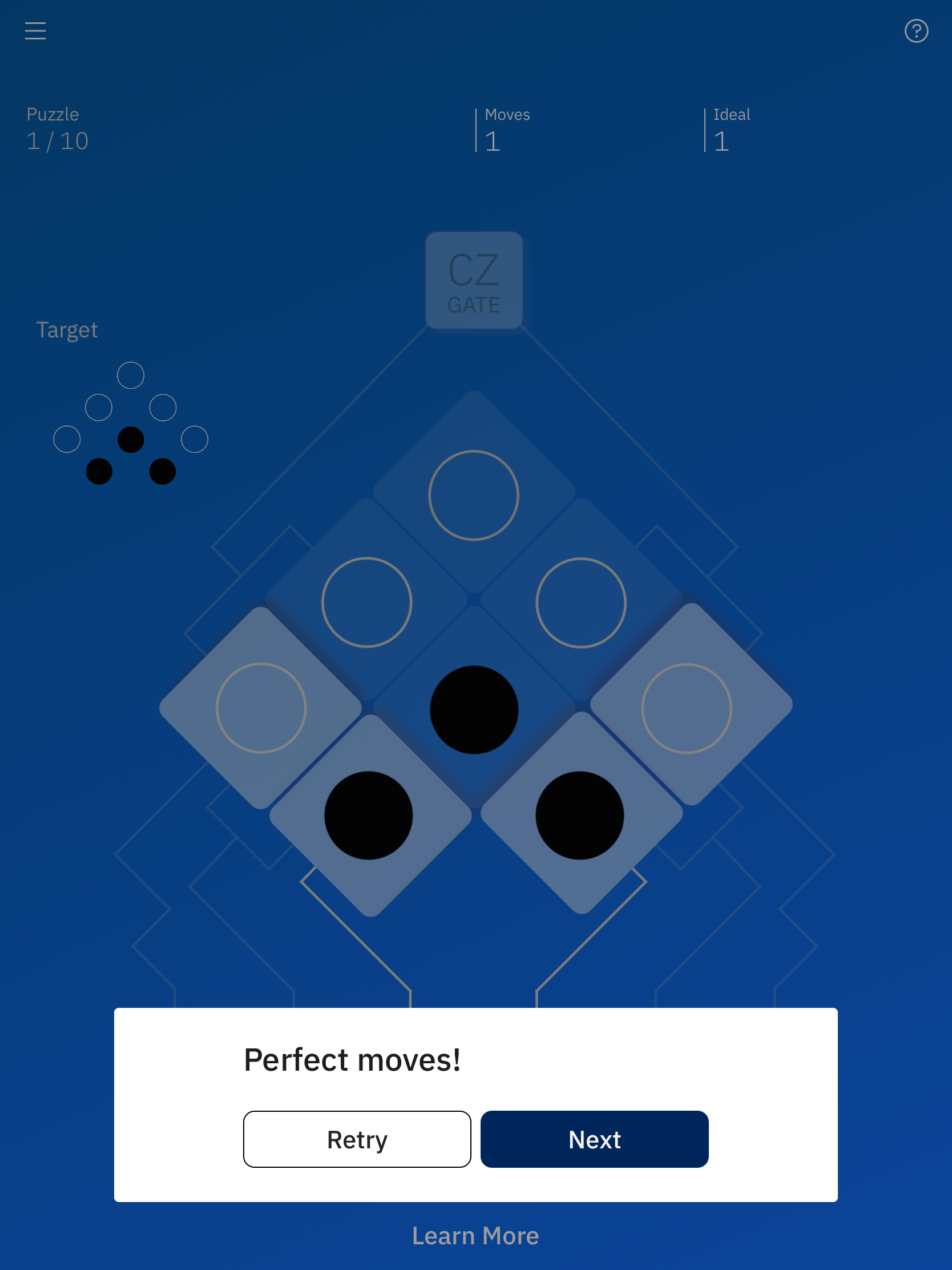
お！クリアしてしまいました。
想像どおり、左下のオセロの色がひっくり返されました。それと一緒に、真ん中にあるオセロもひっくり返りいましたね。どうやら、同じラインに乗っかっているオセロがひっくり返るようです。
これ以外に、random状態のときにXゲートを作用させるとどうなるでしょうか？
こんな状態でやってみます。
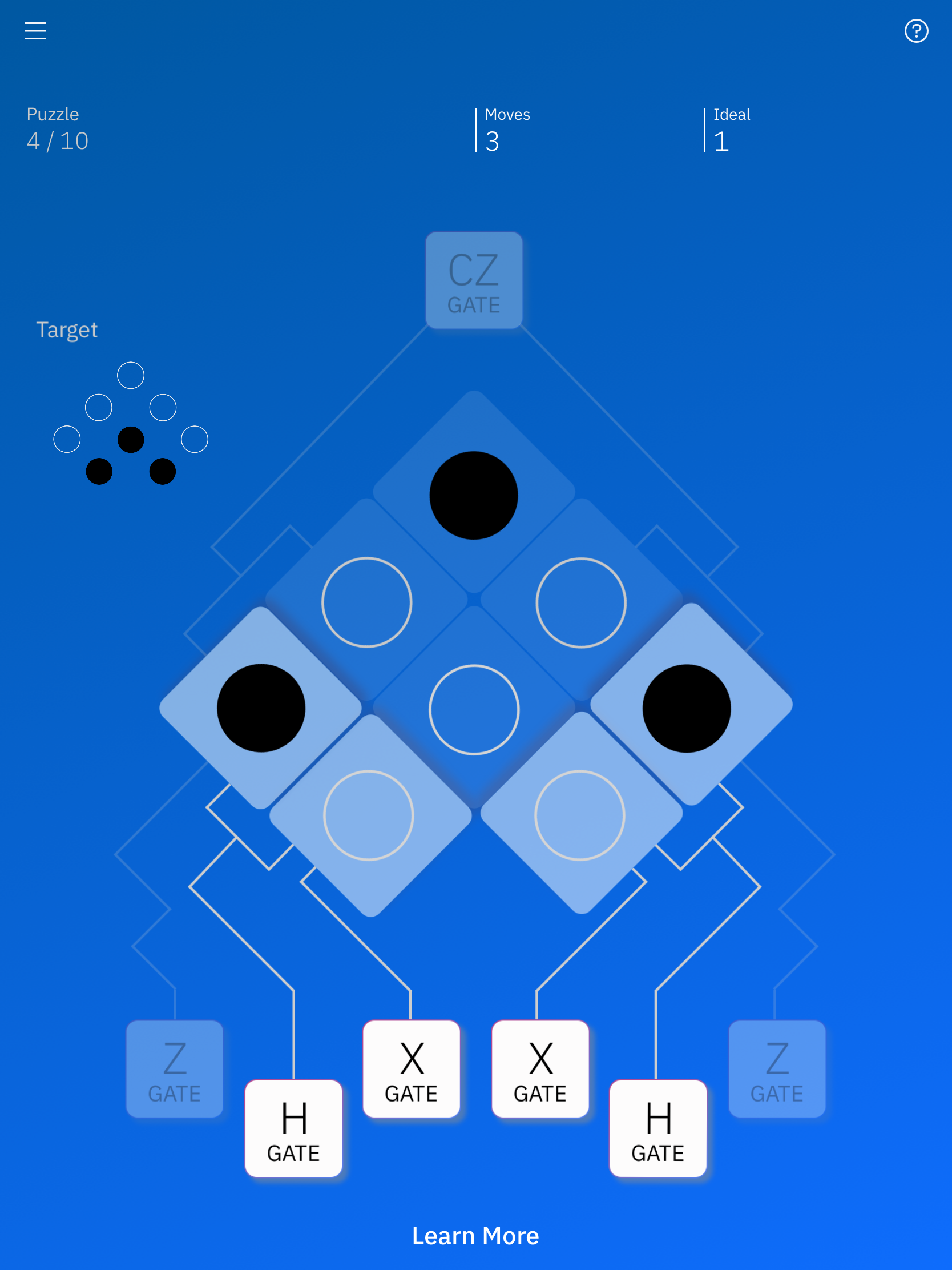
Xゲートを押しても、ramdom状態はramdom状態のままであることがわかります。
Hゲート
Hゲートを使う例です。
初期状態はここからスタートです。
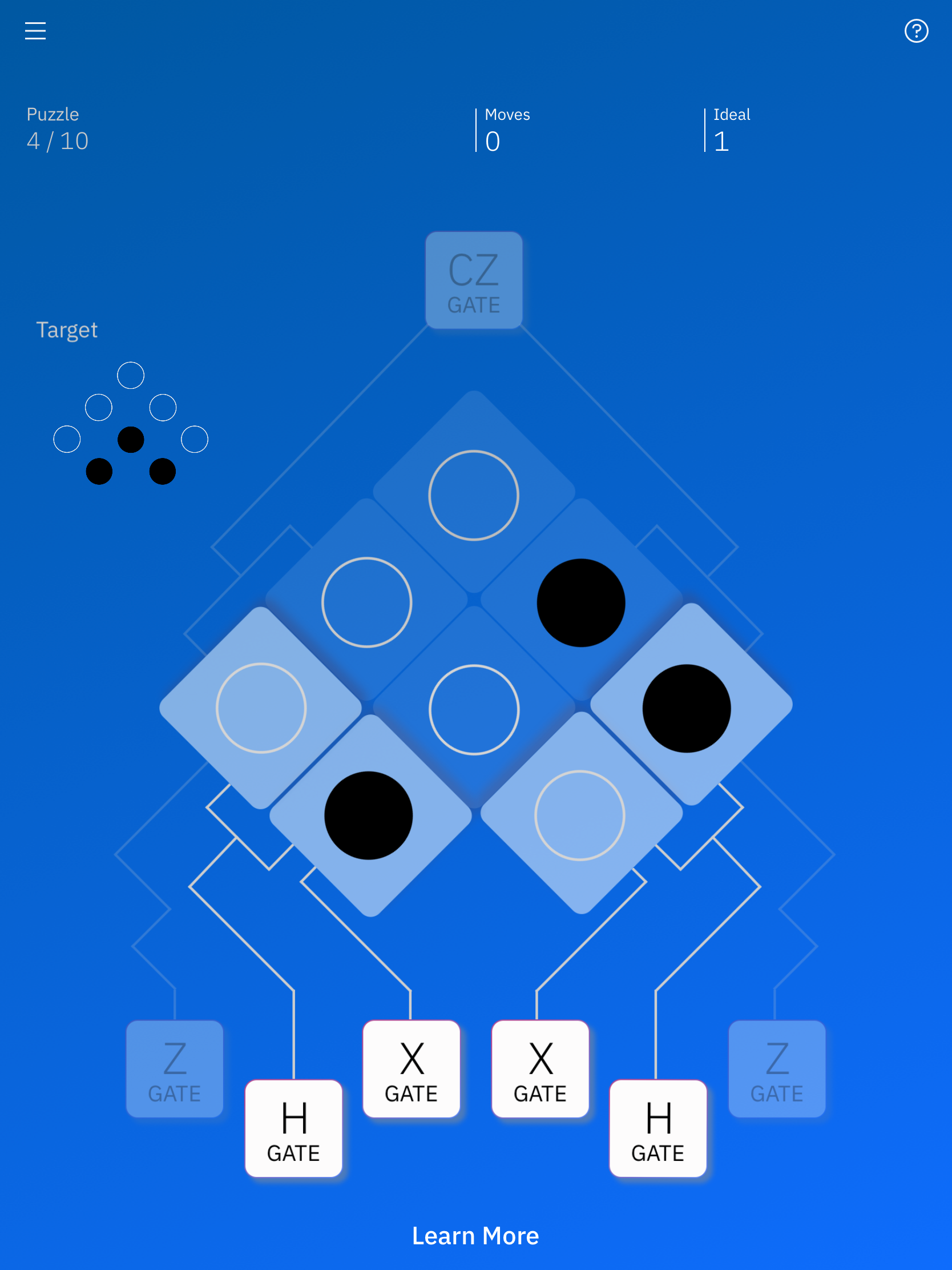
そして、左のHゲートを押してみます。
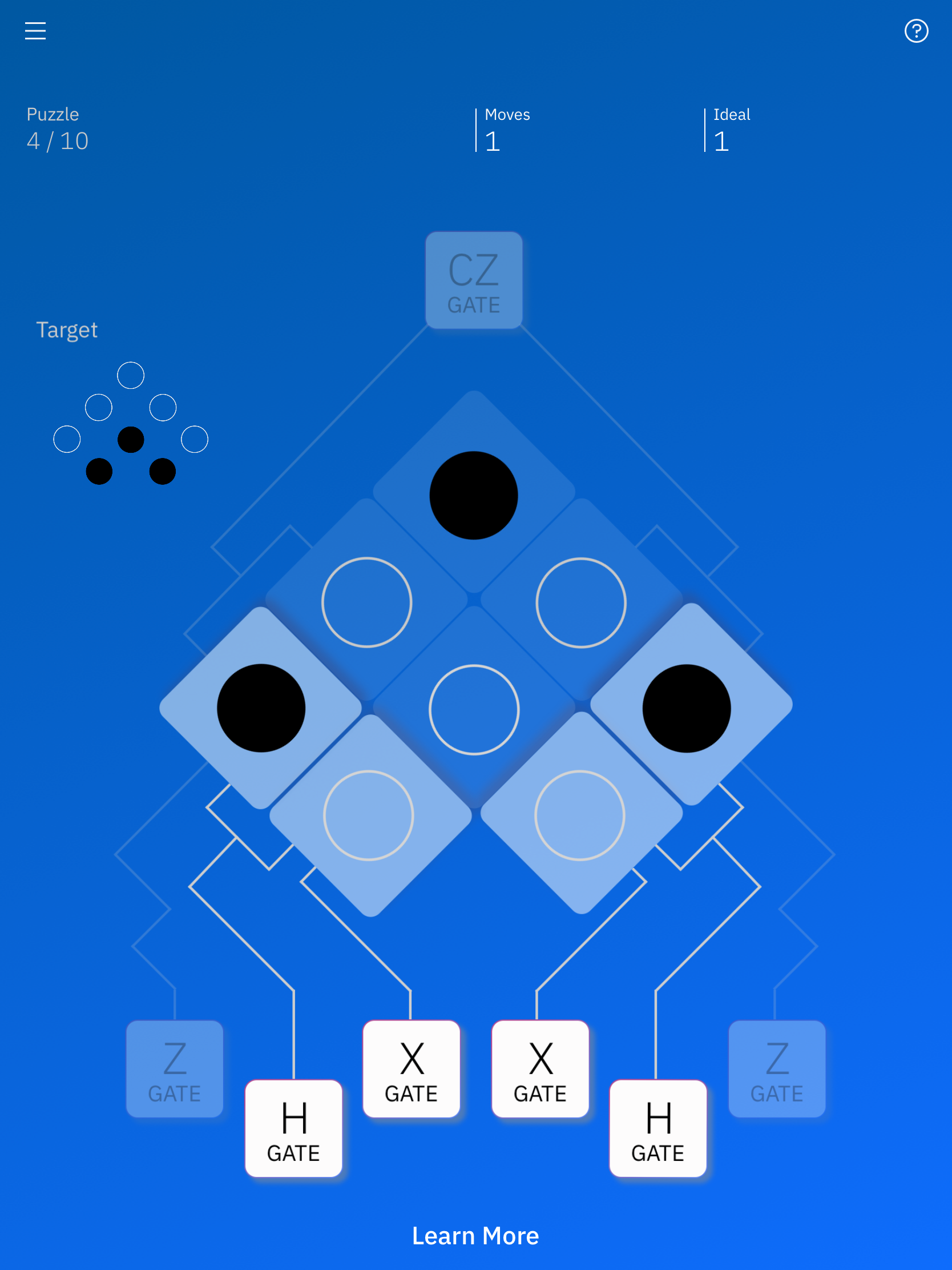
動きを見ると、左下にある２つオセロのラインがそっくり入れ替えられていますね。
Hゲートが、|0>や|1>から重ね合わせ状態（=random状態）にする操作なので、それは理解できます。
Zゲート
次に、Zゲートです。
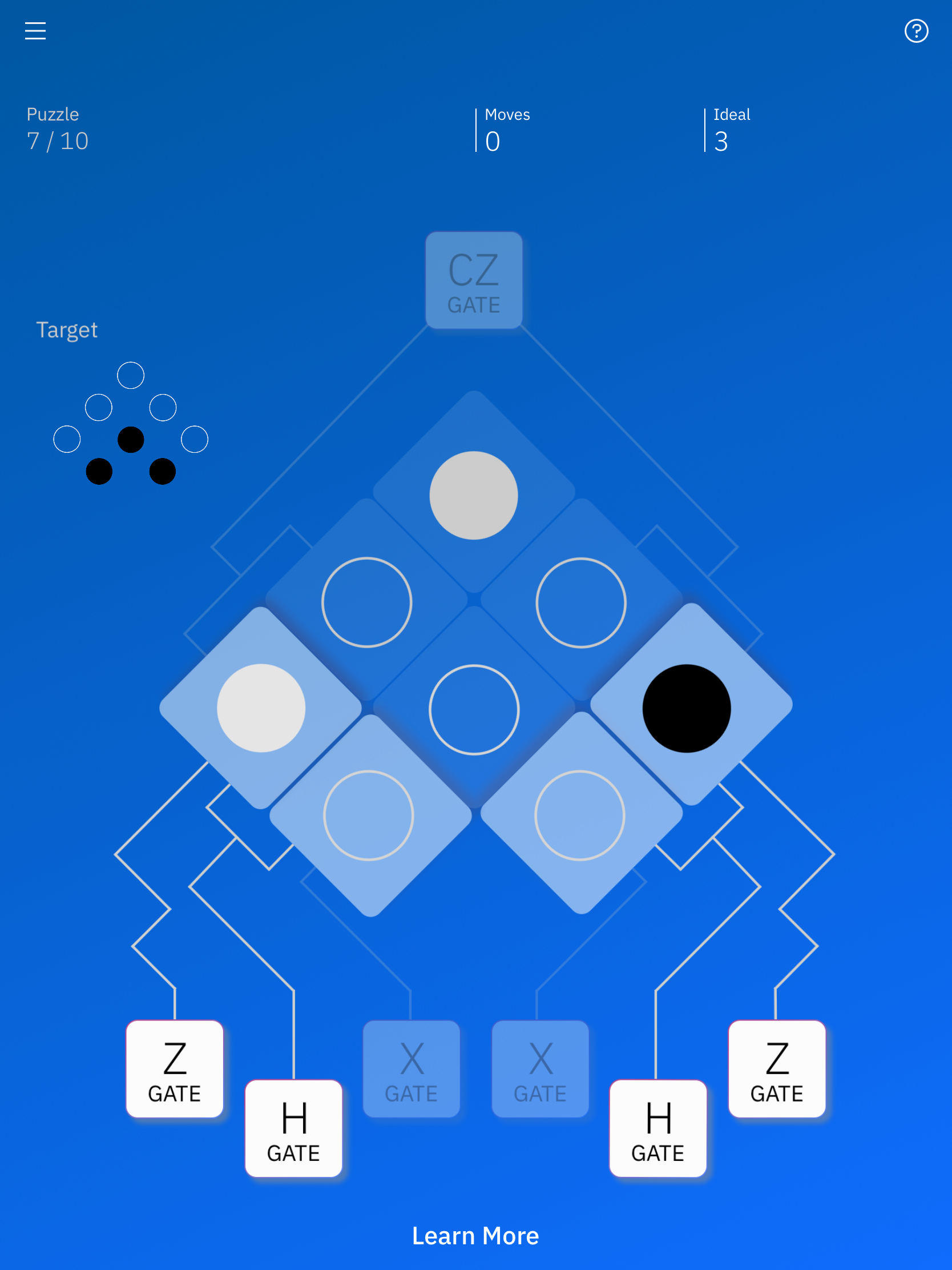
こんな状態からスタートして、左下のZゲートを押してみます。
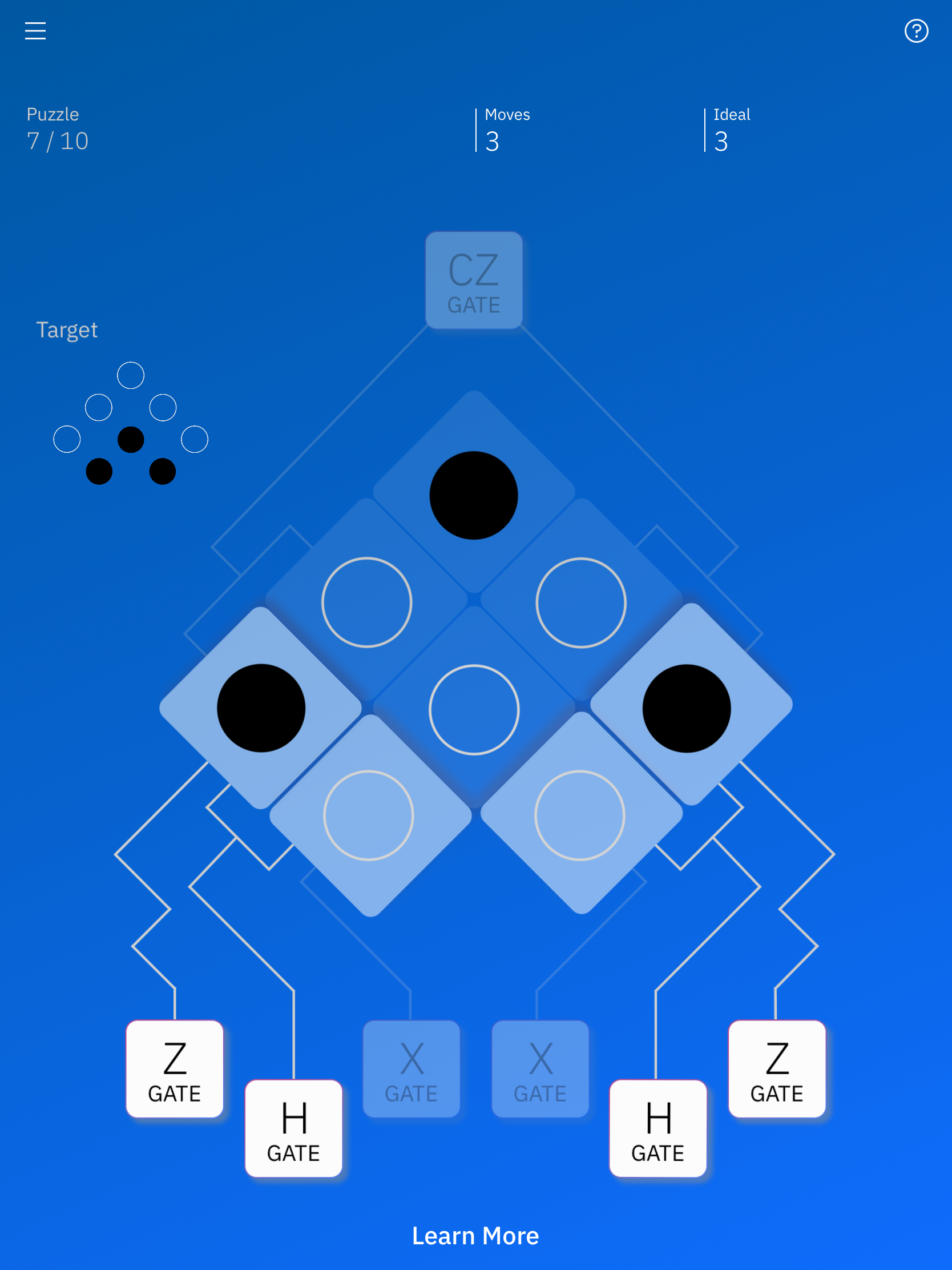
なるほど、白のオセロが黒のオセロになりました。ここはXゲート同じ動きをするようです。
CZゲート
最後に、CZゲートです。
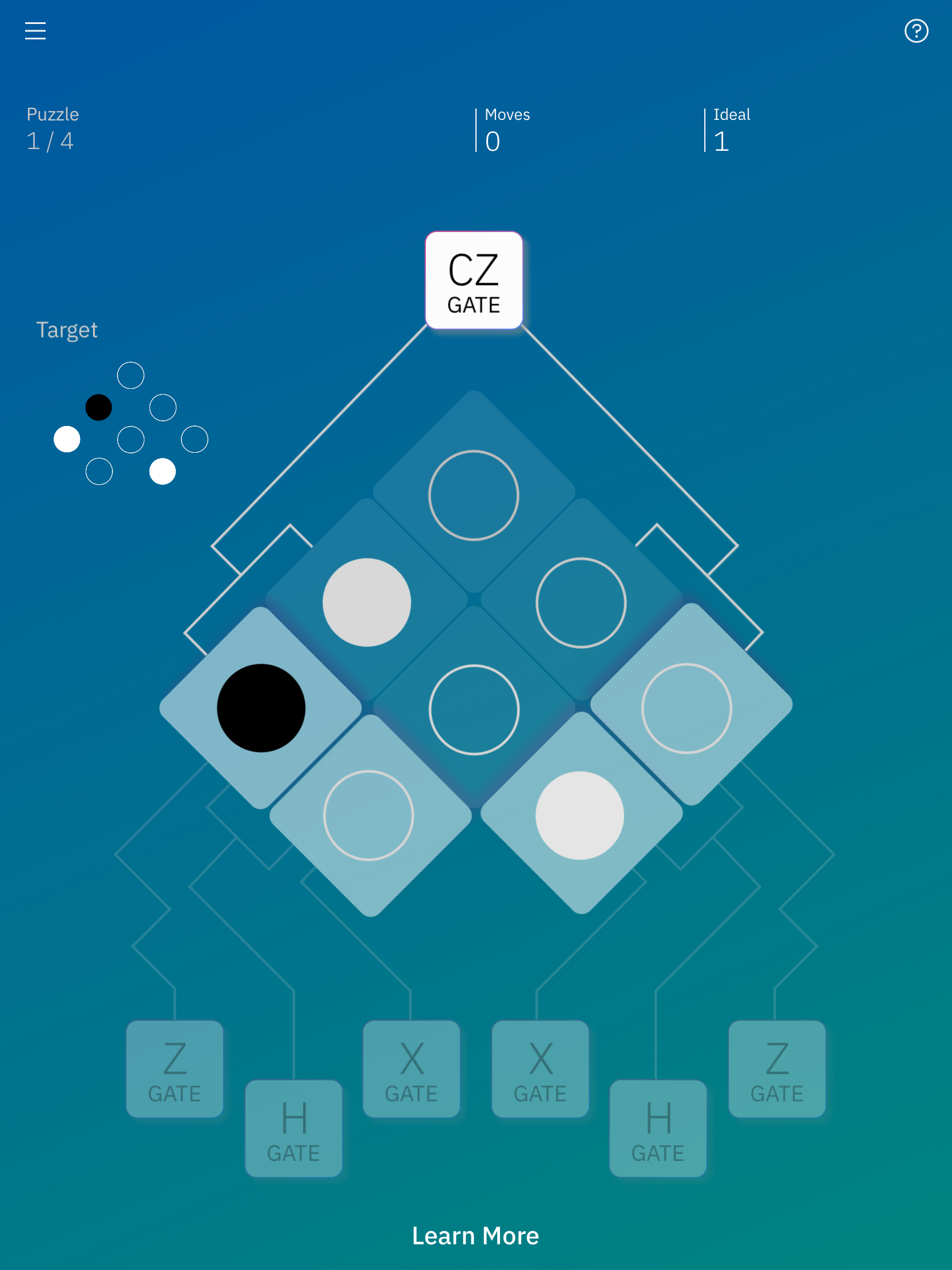
CZゲートを押してみます。
すると、左にあるゲートの白の部分と黒の部分が入れ替わりました。
うん？どういうことだ？
そもそも、CZゲートは、コントロールビットとターゲットビットがあって始めて成立するはずなのですが、これはどちらがコントロールビットでターゲットビットになっているのでしょうか？直感的にはわかりにくいですね。
Hello Quantumを通じて見る、量子ゲートの数理的基本
ここまでの操作を見て、このゲームの量子系は、以下のように見ることになります。
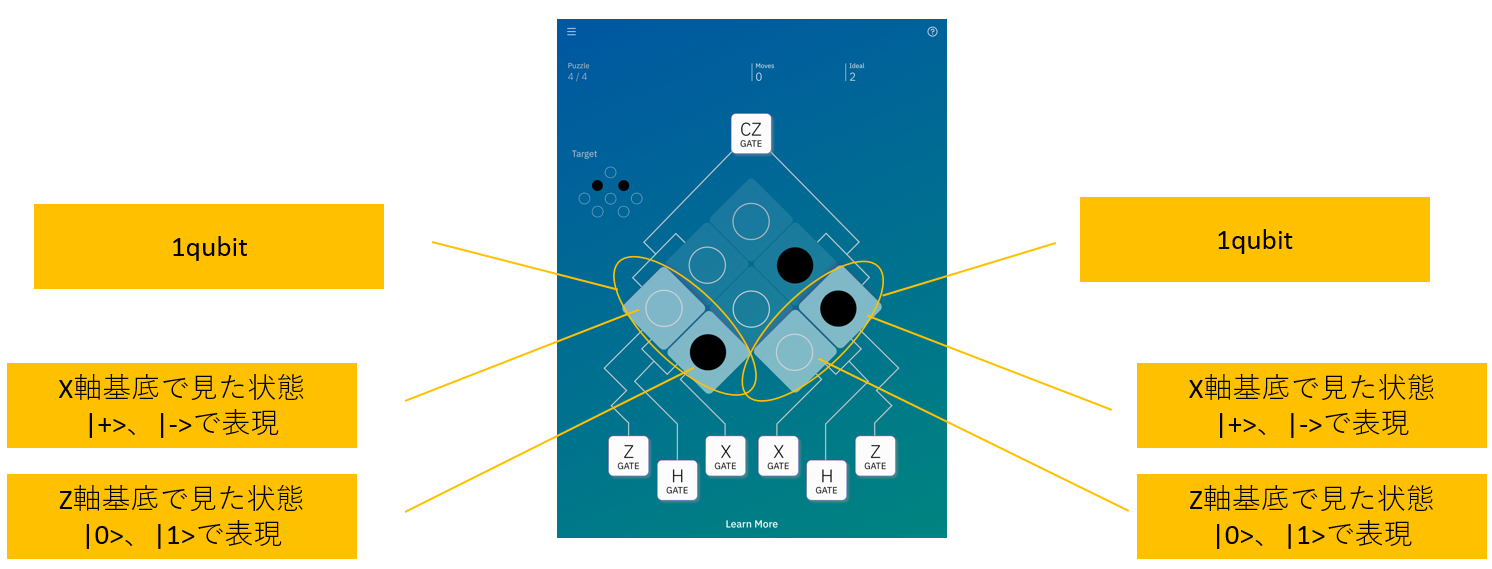
まず、右と左の白枠の部分はそれぞれの1ビットを表しています。なので、2ビットの状態を操作していくことになっています。
そして、Xゲートが繋がっている方は、Z軸基底の方向で見たときの|0>と|1>をそれぞれonとoffにみなしたものと理解できます。
そうなっていることを簡単な計算で確かめてみましょう。
Xゲートの数理
Xがonとoffの入れ替えなので、以下のようにXゲートの操作と同義です。
X|0>=|1> \\
X|1>=|0>
これをrandom状態に作用させて結果が変わらないことが計算でわかります。
X*\frac{1}{\sqrt{2}}(|0>+|1>)=\frac{1}{\sqrt{2}}(X|0>+X|1>)=\frac{1}{\sqrt{2}}(|1>+|0>)
足し算の順番が変わったくらいですが、これであれば、最初と同じ状態です。
なので、これもramdom状態にXゲートを作用させてもそのままであるというゲームの動きと同じであることがわかりました。
Hゲートの数理
一方で、Zゲートに繋がっている方は、X軸基底の方向で見たときの、|+>と|->をそれぞれoffとonにみなしたものと理解できるわけです。
|0>と|1>、|+>と|->はHゲートを通じて次のような関係で繋がっています。
H|0>=\frac{1}{\sqrt{2}}(|0>+|1>)=|+> \\
H|1>=\frac{1}{\sqrt{2}}(|0>-|1>)=|->
逆もまた然りで、|+>と|->はHを使って、|0>と|1>に戻せます。
H|+>=\frac{H}{\sqrt{2}}(|0>+|1>)=\frac{H}{\sqrt{2}}|0>+\frac{H}{\sqrt{2}}|1>=\frac{1}{2}(|0>+|1>+|0>-|1>)=|0> \\
H|->=\frac{H}{\sqrt{2}}(|0>-|1>)=\frac{H}{\sqrt{2}}|0>-\frac{H}{\sqrt{2}}|1>=\frac{1}{2}(|0>+|1>-|0>+|1>)=|1> \\
言い換えると、HゲートはX軸基底での見方とZ軸基底の見方を入れ替える操作とも読み取れるわけです。
Zゲートの数理
Zゲートの操作について見てみます。
Zゲートを|0>に作用させても、そのままだけど、|1>の符号は変える操作をします。つまり、
Z|0>=|0> \\
Z|1>=-|1>
それを踏まえて、|+>と|->にZゲートを作用させるとどうなるかというと、
Z|+>=\frac{Z}{\sqrt{2}}(|0>+|1>)=\frac{1}{\sqrt{2}}(Z|0>+Z|1>)=\frac{1}{\sqrt{2}}(|0>-|1>)=|-> \\
Z|->=\frac{Z}{\sqrt{2}}(|0>-|1>)=\frac{1}{\sqrt{2}}(Z|0>-Z|1>)=\frac{1}{\sqrt{2}}(|0>+|1>)=|+>
つもり、ZゲートとはX軸基底で見たときに、onとoffを入れ替えるという操作に相当していることがわかりますし、ゲーム上での動きと同じであることが見て取れると思います。
CZゲートの数理
ゲームをやっていて一番理解に時間がかかったのは、CZゲートの動きでした。
順を追って説明していきます。
まず、CZゲートとは、コントロールビットが|0>であればターゲットビットの状態は変えず、|1>であればターゲットビット状態にZを作用させるものです。
１つ目の量子ビットとターゲットビット、２つ目の量子ビットをコントロールビットとすると、以下のような数式で表現されます。識別のため、添え字にターゲットビットはtを、コントロールビットにはcをつけておきます。
CZ(|0>_{t} \otimes |0>_{c}) =|0>_{t} \otimes |0>_{c} \\
CZ(|1>_{t} \otimes |0>_{c}) =|1>_{t} \otimes |0>_{c} \\
CZ(|0>_{t} \otimes |1>_{c}) =|0>_{t} \otimes |1>_{c} \\
CZ(|1>_{t} \otimes |1>_{c}) =-|1>_{t} \otimes |1>_{c}
このルールに基づいて、ターゲットビットを|+>と|->にすると、以下のようになることがわかります。少し計算すればすぐに出てきます。
CZ(|+>_{t} \otimes |0>_{c}) =|+>_{t} \otimes |0>_{c} \\
CZ(|->_{t} \otimes |0>_{c}) =|->_{t} \otimes |0>_{c} \\
CZ(|+>_{t} \otimes |1>_{c}) =|->_{t} \otimes |1>_{c} \\
CZ(|->_{t} \otimes |1>_{c}) =|+>_{t} \otimes |1>_{c} \\
ここまでの数理的な計算は機械的な話なので、ルールに沿うだけで計算できます。問題はこれが数式とゲームの動きがどう関係しているかです。
実は、上述した画像に答えがあります。
そこをもう一度良く見てみると、左側の量子ビットがターゲットビットで右側の量子ビットがコントロールビットになっていることがわかるのです！え？わからない？
このゲームをやっていて一番悩んだというか混乱したところが、「どちらがコントロールビットでどちらがターゲットビットなのか」でした。Controlled-hogehogeゲートは、常にコントロールビットとターゲットビットがどの量子ビットに対応しているかが決まっています。
しかしゲームをやっていても、どちらがコントロールビットでターゲットビットであるという表現はされていまん。それもそのはずで、どちらもコントロールにもターゲットにも成りえます。どちらかのビットがZ軸基底の状態になったときに、そちらがコントロールビットになるように動くのです！
それを証明するために、コントロールビットが重ね合わせで表現されていた場合にCZゲートを作用させるとどうなるかです。ターゲットビットは|0>と|1>のどちらかにしてみましょう。すると、、、
CZ(|0>_{t} \otimes |+>_{c}) =\frac{CZ}{\sqrt{2}} (|0>_{t} \otimes (|0>_{c}+|1>_{c}) = \frac{CZ}{\sqrt{2}}( |0>_{t} \otimes |0>_{c} + |0>_{t} \otimes |1>_{c} ) = \frac{1}{\sqrt{2}}( |0>_{t} \otimes |0>_{c} + |0>_{t} \otimes |1>_{c} ) = |0>_{t} \otimes |+>_{c} \\
CZ(|1>_{t} \otimes |+>_{c}) =\frac{CZ}{\sqrt{2}} (|1>_{t} \otimes (|0>_{c}+|1>_{c}) = \frac{CZ}{\sqrt{2}}( |1>_{t} \otimes |0>_{c} + |1>_{t} \otimes |1>_{c} ) = \frac{1}{\sqrt{2}}( |1>_{t} \otimes |0>_{c} - |1>_{t} \otimes |1>_{c} ) = |1>_{t} \otimes |->_{c} \\
CZ(|0>_{t} \otimes |->_{c}) =\frac{CZ}{\sqrt{2}} (|0>_{t} \otimes (|0>_{c}-|1>_{c}) = \frac{CZ}{\sqrt{2}}( |0>_{t} \otimes |0>_{c} - |0>_{t} \otimes |1>_{c} ) = \frac{1}{\sqrt{2}}( |0>_{t} \otimes |0>_{c} - |0>_{t} \otimes |1>_{c} ) = |0>_{t} \otimes |->_{c} \\
CZ(|1>_{t} \otimes |->_{c}) =\frac{CZ}{\sqrt{2}} (|1>_{t} \otimes (|0>_{c}-|1>_{c}) = \frac{CZ}{\sqrt{2}}( |1>_{t} \otimes |0>_{c} - |1>_{t} \otimes |1>_{c} ) = \frac{1}{\sqrt{2}}( |1>_{t} \otimes |0>_{c} + |1>_{t} \otimes |1>_{c} ) = |1>_{t} \otimes |+>_{c}
この結果をよ～く眺めてみると、ある事実に気づきます。コントロールビットとターゲットビットを入れ替えてみてみると気づきます。ターゲットビットが|1>のときに、コントロールビットの|+>と|->が入れ替わっています！
そう、コントロールビットとターゲットビットを入れ替えただけの上述の計算と一緒になるのです！コントロールビットの値でターゲットビットに演算がかかるかを制御していたはずなのに、ターゲットビットの値によってコントロールビットのほうが制御されてしまっているのです！意味が逆転しています！
不思議なことが起こっているように見えますが、これが言わんとしていることは、シンプルです。「CZゲートはどちらがコントロールビットでもどちらをターゲットビットでも良い」ということです！もっと言い換えると、どちらがコントロールだターゲットだと気にする必要はなかったのです。これは量子コンピューターの教科書に載っているぐらいの事実なのでした。
つまり、その事実を忘れていたために、自爆気味に混乱していたことになります。。。
なお、このコントロールビットとターゲットビットを入れ替えても等価であるという事実は、一般のControlled-hogehogeゲートでは通用しない話なので、ご注意ください。
Hello QuantumはQuantum Nativeの学びに役立つか？
取っ掛かりとしては、気軽に触れるの良いと思いますが、これだけで量子コンピューターを理解してどうなるというものではないとは思いました。なので、タイトルに対する答えとしては、入り口としては十分と思いますが、本館的に勉強するとなると、別の仕組みが必要になります。
一方で、ゲーム上の動作とここで導出した数式を対比させてみると、初心者にとって見通しが立ちやすいことあるとは思います。
なので、こうやって整理してみると、とても良くできていることがわかりました。
Hello Quantumを通じて、Quantum Nativeの若者がたくさん出てきてくれることを祈るばかりです。
（将来的には、ビットが重なり合っていることが普通になって、重なり合っていない古典ビットが馬鹿にされる時代が来るかもしれない恐怖はありますが）
最後に、このHello Quantumに１つ不満があるすれば、解説がわかりにいくということでしょうか。初学者を対象としているのかしれませんが、中級者以上の少し慣れた人では逆に直感的にはわかりにくい説明に思えました。
他に初学者が勉強するツールはある？
あります。
ここで動きと数式を理解したら、次はEntanglionというボードゲームがありますので、そちらに進むと良いでしょう。こちらも、IBM Researchが開発したものです。IBMはシステムだけではなく、ボードゲームまで開発してるんですね！
https://entanglion.github.io/
なお、Githubから画像をダウンロードして印刷すれば、ほぼタダで遊べます！
https://github.com/Entanglion/entanglion
いずれ、こちらの連載にENTANGLIONの解説を書いてみたいと思います。
某量子コンピューターのコミュニティでゲーム大会みたいな会を催そうとしているので、それまでに勉強してこちらの記事にまとめていきたいと思います。
最後に余談ですが、噂によると、プロ中のプロの量子コンピューター研究者がEnatnglionはまっているとかｗ