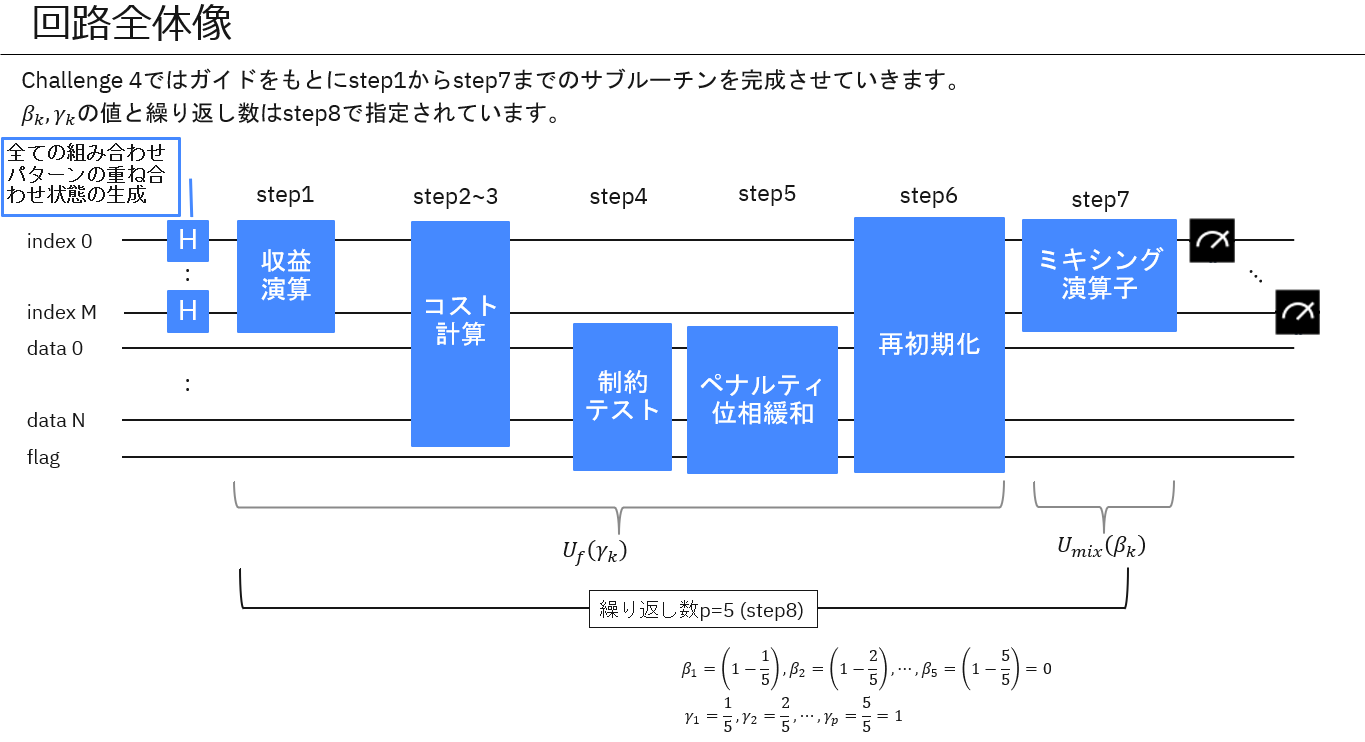
量子コンピューターアドベントカレンダー最終日25日の投稿になります。
はじめに/IBM Quantum Challenge 2021 fallとは
IBM Quantum Challengeとは、IBMが主催する量子コンピュータープログラミングコンテストです。
ここ2年ほどは5月と11月に、半年に1回ペースで開催されています。(ちなみに、2021年は9月にIBM Quantum Challenge Africaというアフリカにちなんだ問題をQiskitで解くコンテストが開催されました)
実は5月に開催されたときにも、最終問題で最高スコアを出せたので解説記事を書いております。今回も全体15位というそこそこ良い結果が出せたので、その部分の解説記事を書いてみようと思い至りました。

IBM Quantum Challenge 2021 fallの概要とコンテンツは以下になります。
https://challenges.quantum-computing.ibm.com/fall-2021
https://github.com/qiskit-community/ibm-quantum-challenge-fall-2021
どんな問題が出てるの?
IBM Quantum Challenge 2021 fallでは、Qiskitが主に注力しているテーマとして、金融オプション計算、量子化学計算、機械学習、最適化問題に焦点を当てて、それぞれのテーマに関連する問題を解いていくスタイルになります。もちろん全てに精通しているスーパーマンは世界を見渡してもほぼいないはずなので、丁寧な誘導と解説が付いています。
特に、これらの注力している分野においてはQiskitには問題を解くための専用のクラスが用意されていて、計算に必要なインプットをクラスをインスタンス化するときに指定してあげれば、問題が解けるようになっています。ほとんどの問題は、そのクラスを使い方のレクチャーがあり、実際に自分で問題を解くためにコーディングをすることで問題を解いていきます。
ですので、初心者がQiskitの使い方を学ぶ目的としても問題のレベルは適切にされており、教育目的としても、十分な内容と言えます。
さて、参加者はこれらの4つのテーマの問題を解いていき、4-bという問題まで解けると晴れてゴールとなります。そこまでゴールした人には以下のようなデジタルバッジが付与されます。(その前であっても、解けた所までに応じてバッジが用意されています。)
このバッジ自体は参加者の半数近くが取得できており、このChallengeを通じてQiskitに慣れ親しんだことと思います。
しかし、このChallengeはここでは終わらなかったのです。4-bは言わばRPGのラスボスですが、その後に裏ボスとも言える4-cという問題が控えていたのです。
なお、この4-cで最終順位が決まりますので、腕に覚えのあるQuantum Developerは挙って挑戦したのですが、、、多くの猛者たちが返り討ちにあい、結果として1293人中49人しか正解に辿り着けませんでした。正解率4%以下は「ひぐらしのなく頃に」の正解率に匹敵するぐらいに難問であったことが伺えます。半数が4-bまで解けていたのにも関わらず・・・。実際に4-cだけが、それまでとは異なる様相を示しており、多くの参加者を苦しめていました。
そんな中、著者は何とかこの問題を解くことができ、最終的に15位という順位で終わることができました。
ここでは、その内容を**"雑に"**解説していこうと思います。アドベントカレンダーの投稿予定日に執筆開始して、その日の投稿に間に合わせるために、あまり丁寧には書いている時間が無かったので、ご容赦ください!!!リクエストがあれば、もう少し丁寧に書き直します!
4-cを解説する
では、ここから4-cを解説していきます。
その前に、どんな問題かを見て行きましょう。
詳細は公式GitHub上のjupyter notebookを参照してください。
https://github.com/qiskit-community/ibm-quantum-challenge-fall-2021/blob/main/content/challenge-4/challenge-4-ja.ipynb
ポイントは、2つの電池システムがあり、必ずどちらか一方のの電池を使う条件のもとで、それぞれに使うごとに異なる利益を出し、それぞれ異なる劣化をするようなシチュエーションで、利益を最大化する解を見つけてください、という問題です。いわゆる数理最適化に関する問題です。
この問題は、4-bまでを解くと、ナップサック問題として定式される設定になっています。ナップサック問題の詳細はnotebookに書かれているので、そちらを読んでいただくとして、簡単に言えば「容量の上限がある中で利益を最大にする積み方を求める組み合わせ最適化問題」というものです。ここで、容量の上限を超えるものは解の候補になりません。
しかし、問題によっては上限を超えても良いケースを考えることもできます。つまり、上限を超えたら、利益に何らかのペナルティを与えることで利益を減らすというケースです。一般的にこういったシチュエーションはありそうに思えますし、実際にこの4-cではそれが設定になります。このような設定を「緩和されたナップサック問題」と呼ばれる問題になります。
4-bまではナップサック問題クラスがあるので、それを使えば解けるのですが、4-cは緩和されたナップサック問題の量子版をスクラッチでコーディングしていくことになります。
背景
問題の背景はこの通りです。ここではQAOAという用語は出てきていますが、あまり気にしないでも大丈夫です。
サンプルは次のようなものが与えられています。
instance_examples = [
{
'L1': [3, 7, 3, 4, 2, 6, 2, 2, 4, 6, 6],
'L2': [7, 8, 7, 6, 6, 9, 6, 7, 6, 7, 7],
'C1': [2, 2, 2, 3, 2, 4, 2, 2, 2, 2, 2],
'C2': [4, 3, 3, 4, 4, 5, 3, 4, 4, 3, 4],
'C_max': 33
},
{
'L1': [4, 2, 2, 3, 5, 3, 6, 3, 8, 3, 2],
'L2': [6, 5, 8, 5, 6, 6, 9, 7, 9, 5, 8],
'C1': [3, 3, 2, 3, 4, 2, 2, 3, 4, 2, 2],
'C2': [4, 4, 3, 5, 5, 3, 4, 5, 5, 3, 5],
'C_max': 38
},
{
'L1': [5, 4, 3, 3, 3, 7, 6, 4, 3, 5, 3],
'L2': [9, 7, 5, 5, 7, 8, 8, 7, 5, 7, 9],
'C1': [2, 2, 4, 2, 3, 4, 2, 2, 2, 2, 2],
'C2': [3, 4, 5, 4, 4, 5, 3, 3, 5, 3, 5],
'C_max': 35
}
]
順位はどうやって付くのか
スコアリングルールは以下のようになっています。2段階のステップを踏む必要があります。

ゴチャゴチャ書いてあるので、掻い摘んでお伝えすると、まず1段目のステップとして、同じコードで複数の隠された解答用のデータを使って、ある程度の正解率が担保されていること、がスコア算出の必要条件です。つまり、下手なコードを書いても正解率が下回るので、その場合はここで弾かれます。正解率の算出の細かい考え方を上で伝えてくれています。

ある程度の正解率を超えたケースについては、回路の深さ(クリティカルパス)の50倍、CNOTの数の10倍、後は単一ゲートの数の総和をスコアとして算出します。
このスコアが小さければ小さいほど、処理が効率化されているので、このChallengeでは良いコードと評価される仕組みになっています。
解法の方針

ここでは丁寧に問題の定式化と解法の方針が解説されています。
基本的にはこの流れに沿って解いていくことで問題はありません。
定式化は書かれている通りですが、方針は基本のユニットとしてブレークダウンされているので、それを1つずつコーディングすることになります。
なお、この問題はこの論文:Knapsack Problem variants of QAOA for battery revenue optimisationが題材になっています。著者はこの論文を中心に読み込みながら、解法を作っていきました。
著者の解法
著者の方針としては、誘導に従いその順序で解いています。ただ、部分部分で自分が書きやすい方針にするために端折ったりしています。
まずはこちらが、著者の提出版の解答です。
def solver_function(L1: list, L2: list, C1: list, C2: list, C_max: int) -> QuantumCircuit:
# the number of qubits representing answers
index_qubits = len(L1)
# the maximum possible total cost
max_c = sum([max(l0, l1) for l0, l1 in zip(C1, C2)])
min_c = sum([min(l0, l1) for l0, l1 in zip(C1, C2)]) # 最小コストの計算。コストは全てのパターンに必ずこの値以上になる
# the number of qubits representing data values can be defined using the maximum possible total cost as follows:
data_qubits = math.ceil(math.log(max_c, 2)) + 1 if not max_c & (max_c - 1) == 0 else math.ceil(math.log(max_c, 2)) + 2
#tmp_qubits = 28-data_qubits-index_qubits-1 # 補助ビット用qubit
c_flag = (C_max < max_c) # ルールの欠陥になっているデータが無いかを確認するフラグ(欠陥データは無い)
### Phase Operator ###
# return part
#def phase_return():
def phase_return(index_qubits: int, gamma: float, L1: list, L2: list, to_gate=True): #-> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qc = QuantumCircuit(qr_index)
##############################
### U_1(gamma * (lambda2 - lambda1)) for each qubit ###
# ここにコードを書いてください
for i in range(index_qubits):
if L2[i] != L1[i]:
qc.u1(-1*gamma*(L2[i]-L1[i]),qr_index[i])
##############################
#qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
return qc.to_gate(label=" phase return ") if to_gate else qc
##############################
def cost_calculation(index_qubits: int, data_qubits: int, list1: list, list2: list, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qc = QuantumCircuit(qr_index, qr_data)
qc.h(qr_data[:]) # QFTの実行。ただし、初期が|0>なので、QFTの代わりにHadamardゲートで代用可能かつ処理は最小で済む
N=2**(data_qubits)
for d in range(data_qubits):
qc.u1(2*math.pi*min_c*(2**d)/N,qr_data[d]) # 最初に最小コストを全ての状態に足し込んでおく
for i, (val1, val2) in enumerate(zip(list1, list2)):
min_val = min(val1,val2)
##############################
### Add val2 using const_adder controlled by i-th index register (set to 1) ###
# Put your implementation here
#以下はval1かval2の少なくともどちら1つは必ずmin_valに一致するので、どちらか一方しかcu1ゲートを作らない。これでcu1を半分削減できる
for d in range(data_qubits):
if val2-min_val > 0:
qc.cu1(2*math.pi*(val2-min_val)*(2**d)/N,qr_index[i],qr_data[d])
##############################
qc.x(qr_index[i])
##############################
### Add val1 using const_adder controlled by i-th index register (set to 0) ###
# Put your implementation here
for d in range(data_qubits):
if val1-min_val> 0:
qc.cu1(2*math.pi*(val1-min_val)*(2**d)/N,qr_index[i],qr_data[d])
##############################
qc.x(qr_index[i])
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
return qc.to_gate(label=" Cost Calculation ") if to_gate else qc
def constraint_testing(data_qubits: int, C_max: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_data = QuantumRegister(data_qubits, "data")
qr_f = QuantumRegister(1, "flag")
qc = QuantumCircuit(qr_data, qr_f)
##############################
### Set the flag register for indices with costs larger than C_max ###
# Put your implementation here
N=2**data_qubits
#次に上位の閾値までの差分(diff)を計算
if 2**math.ceil(math.log(C_max,2)) == C_max:
diff = 2**math.ceil(math.log(C_max,2))*2 - C_max - 1
threshold = math.ceil(math.log(C_max,2)) + 1
else:
diff = 2**math.ceil(math.log(C_max,2)) - C_max - 1
threshold = math.ceil(math.log(C_max,2))
# データqubitにdiffを足し込み、閾値を2^cに揃える。ただし、diffが0(C_max=2^c-1のとき)なら何もしないようにして不要なゲートは作らないようにする
if diff > 0:
for d in range(data_qubits):
qc.u1(2*math.pi*diff*(2**d)/N,qr_data[d])
# 全てのフラグを一度1にセット
qc.x(qr_f[0])
# 逆QFTによって位相の肩に乗っている値を計算基底状態にエンコード
iqft = QFT(data_qubits,inverse=True)
iqft = transpile(iqft, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
qc.append(iqft.to_gate(label='IQFT'),qr_data[:])
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
# 2^cよりも大きい量子ビットを一度反転させて、コスト+diff<=2^cではフラグを反転させて0にする。逆にコスト+diff>2^cではフラグは1のままにする
qc.x(qr_data[threshold:])
qc.mct(qr_data[threshold:],qr_f)#,ancilla_qubits=qr_tmp[:],mode='recursion') # 補助ビットを使ってmctを最適化しようしたしたが効果なし。
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
return qc.to_gate(label=" Constraint Testing ") if to_gate else qc
def penalty_dephasing(data_qubits: int, alpha: float, gamma: float, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_data = QuantumRegister(data_qubits, "data")
qr_f = QuantumRegister(1, "flag")
qc = QuantumCircuit(qr_data, qr_f)
##############################
### Phase Rotation ###
# Put your implementation here
N = 1
for i in range(data_qubits):
qc.cu1(alpha*gamma*N,qr_f[0],qr_data[i])
N*=2
qc.u1(-alpha*gamma*(2**math.ceil(math.log(C_max,2))) ,qr_f[0])
##############################
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
return qc.to_gate(label=" Penalty Dephasing ") if to_gate else qc
def reinitialization(index_qubits: int, data_qubits: int, C1: list, C2: list, C_max: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qr_f = QuantumRegister(1, "flag")
qc = QuantumCircuit(qr_index, qr_data, qr_f)
##############################
### Reinitialization Circuit ###
# Put your implementation here
qc.append(cost_calculation(index_qubits,data_qubits,C1,C2),qr_index[:]+qr_data[:])
qc.append(constraint_testing(data_qubits,C_max),qr_data[:]+qr_f[:])
qc = qc.inverse()
#qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
##############################
return qc.to_gate(label=" Reinitialization ") if to_gate else qc
### Mixing Operator ###
#def mixing_operator():
##############################
### TODO ###
### Paste your code from above cells here ###
def mixing_operator(index_qubits: int, beta: float, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qc = QuantumCircuit(qr_index)
##############################
### Mixing Operator ###
# Put your implementation here
if beta > 0:
qc.rx(2*beta,qr_index)
##############################
return qc.to_gate(label=" Mixing Operator ") if to_gate else qc
##############################
qr_index = QuantumRegister(index_qubits, "index") # index register
qr_data = QuantumRegister(data_qubits, "data") # data register
qr_f = QuantumRegister(1, "flag") # flag register
#qr_tmp = QuantumRegister(tmp_qubits, "tmp") # 補助ビット用
cr_index = ClassicalRegister(index_qubits, "c_index") # classical register storing the measurement result of index register
cr_flag = ClassicalRegister(1,"f_index")
cf_data = ClassicalRegister(data_qubits, "c_data")
qc = QuantumCircuit(qr_index, qr_data, qr_f, cr_index)#qr_tmp, cr_index)
### initialize the index register with uniform superposition state ###
qc.h(qr_index)
### DO NOT CHANGE THE CODE BELOW
p = 5
alpha = 1
for i in range(p):
### set fixed parameters for each round ###
beta = 1 - (i + 1) / p
gamma = (i + 1) / p
### return part ###
qc.append(phase_return(index_qubits, gamma, L1, L2), qr_index)
### step 1: cost calculation ###
qc.append(cost_calculation(index_qubits, data_qubits, C1, C2), qr_index[:] + qr_data[:])
### step 2: Constraint testing ###
qc.append(constraint_testing(data_qubits, C_max), qr_data[:] + qr_f[:])
### step 3: penalty dephasing ###
qc.append(penalty_dephasing(data_qubits, alpha, gamma), qr_data[:] + qr_f[:])
### step 4: reinitialization ###
qc.append(reinitialization(index_qubits, data_qubits, C1, C2, C_max), qr_index[:] + qr_data[:] + qr_f[:])
### mixing operator ###
qc.append(mixing_operator(index_qubits, beta), qr_index)
### measure the index ###
### since the default measurement outcome is shown in big endian, it is necessary to reverse the classical bits in order to unify the endian ###
qc.measure(qr_index, cr_index[::-1])
return qc
難易度が高いのがstep2~3とstep4になると思います。これの実装方針を正しく理解しコーディングできるかがポイントだったでしょう。
計算前の準備
まず提出関数の最初の部分の準備になります。
def solver_function(L1: list, L2: list, C1: list, C2: list, C_max: int) -> QuantumCircuit:
# the number of qubits representing answers
index_qubits = len(L1)
# the maximum possible total cost
max_c = sum([max(l0, l1) for l0, l1 in zip(C1, C2)])
min_c = sum([min(l0, l1) for l0, l1 in zip(C1, C2)]) # 最小コストの計算。コストは全てのパターンに必ずこの値以上になる
# the number of qubits representing data values can be defined using the maximum possible total cost as follows:
data_qubits = math.ceil(math.log(max_c, 2)) + 1 if not max_c & (max_c - 1) == 0 else math.ceil(math.log(max_c, 2)) + 2
#tmp_qubits = 28-data_qubits-index_qubits-1 # 補助ビット用qubit
c_flag = (C_max < max_c) # ルールの欠陥になっているデータが無いかを確認するフラグ(欠陥データは無い)
基本的には、用意されたものを使えば良いのですが、ここでは後で効率化の工夫のために、min_cという値を定義し、事前に算出しています。これは全てのパータンの中でコストの最小値を表しますが、オフセットとして利用することでコストを下げるために利用できます。step2-3で出てきます。
step1 利益計算パート
def phase_return(index_qubits: int, gamma: float, L1: list, L2: list, to_gate=True): #-> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qc = QuantumCircuit(qr_index)
##############################
### U_1(gamma * (lambda2 - lambda1)) for each qubit ###
# ここにコードを書いてください
for i in range(index_qubits):
if L2[i] != L1[i]:
qc.u1(-1*gamma*(L2[i]-L1[i]),qr_index[i])
##############################
return qc.to_gate(label=" phase return ") if to_gate else qc
step2-3コストの計算
山場の1つです。ここでは、各パターンごとのコスト値をデータ量子ビットに計算基底状態(2進数値の状態)としてエンコードすることを目指します。
もう少し細かく分解すると、以下のような流れになっています。
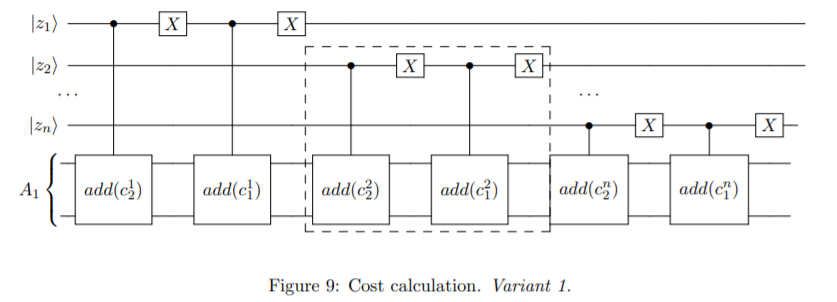
今回の実装上の誘導では、QFT加算器(QFT Adder)を使うことが推奨されています。
QFT加算器の詳細はこちらがわかりやすいです。
https://zenn.dev/bobo/articles/6682d6f3cd7e6c
QFT加算器は、事前にQFTを施した状態に対して、位相に追加したい値を”適切に”足し込む(位相を変化させる)ことで、逆QFTをした後に計算基底状態が、その値が足し込まれた状態を実現することができます。これは回路がシンプルで、ゲート数が安定しやすいメリットがあります。ただ、慣れていないと実装が混乱しやすいです。
実際にやっていることは、それだけでQFT->位相への値の足し込みをしているだけになります。コードを見てみましょう。
def cost_calculation(index_qubits: int, data_qubits: int, list1: list, list2: list, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qc = QuantumCircuit(qr_index, qr_data)
qc.h(qr_data[:]) # QFTの実行。ただし、初期が|0>なので、QFTの代わりにHadamardゲートで代用可能かつ処理は最小で済む
N=2**(data_qubits)
for d in range(data_qubits):
qc.u1(2*math.pi*min_c*(2**d)/N,qr_data[d]) # 最初に最小コストを全ての状態に足し込んでおく
for i, (val1, val2) in enumerate(zip(list1, list2)):
min_val = min(val1,val2)
##############################
### Add val2 using const_adder controlled by i-th index register (set to 1) ###
# Put your implementation here
#以下はval1かval2の少なくともどちら1つは必ずmin_valに一致するので、どちらか一方しかcu1ゲートを作らない。これでcu1を半分削減できる
for d in range(data_qubits):
if val2-min_val > 0:
qc.cu1(2*math.pi*(val2-min_val)*(2**d)/N,qr_index[i],qr_data[d])
##############################
qc.x(qr_index[i])
##############################
### Add val1 using const_adder controlled by i-th index register (set to 0) ###
# Put your implementation here
for d in range(data_qubits):
if val1-min_val> 0:
qc.cu1(2*math.pi*(val1-min_val)*(2**d)/N,qr_index[i],qr_data[d])
##############################
qc.x(qr_index[i])
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
return qc.to_gate(label=" Cost Calculation ") if to_gate else qc
ここでは、まだこの後のステップでコストに追加の足し込みをするために、逆QFTはしていません。
step2~3での計算の工夫
実は、ここでスコア下げるために2つの工夫をしています。
1つはQFTを別の処理に置き換えていることです。これは、初期状態が|00…000>のときにはQFTを”真面目に”実行すると均等な重ね合わせ状態が生成されます。つまり、全ての量子ビットにHadmardゲートを1回ずつかけたのと同じ状態が生成されます。なので、Hadmardゲートに置き換えてゲート数を減らしています。これでかなりのコストが削れます。(実際には100000ぐらい)
QFTを真面目にゲートで書き出すと、CNOTを$O(n^2)$のオーダーで増えるのでコストにかなり影響するのがわかると思います。
2つ目は、準備のときに使ったmin_cを利用し、QFT加算器で位相に足し込む回数を半分に減らしたことです。与えられた初期のnotebookを見ていると、インデックス量子ビットの状態を変えて1回ずつコストを足し込んでいくように書かれているのですが、これはある意味罠です。今回は2つの電池のどちらかは必ず使われる前提になっているので、必ず使われる分はどちらの電池を使うか(組み合わせのパータン)に関係なくオフセットと見なして、最初に足し込んでおけばよいのです。それにより、大幅なCNOTの削減が可能です。ただ、最小値からの差分は足し込む必要があるので、そのケースになっている組み合わせにはCUゲートを使って1回足し込む必要があります。
これって競技プログラミングでよく出てきそうな処理を少なくするアイデアですよね!
実は、これに気づくと、スコアが1/3ぐらいに減ります。 (コード上の処理数は半分だけど、回路の深さが浅くなり、CNOTも減るので、劇的に超すあが減ります。)
著者も最初からこれには気づいていなかくて、一度正解が出せるようになってから、この改良をしてスコアを下げることができました。
step4 制約テスト
山場の2つ目です。
ここではデータ量子ビットにエンコードしたコストを元に、フラグ量子ビットに「コストが閾値を超えているかどうか」を登録します。
ここで少し工夫が必要です。
例えば、閾値が18だったとしましょう。8量子ビット使うとして、|18>は|00010010>と表せます。
ここで|20>=|00010100>という状態が作れたとして、18を超えたことをどうフラグに伝えるでしょうか。シンプルに思いつくこととしては、CNOTを使うことになると思いますが、どの量子ビットにどうやるかが、見えてこないと思います。そこで発想を変えます。
結論としては、元の閾値の値に適当な値を足し込んで、2のべき乗($2^c$)となる適当な値を見つけることです。つまり、$C_{max} + w = 2^c$となる$w$を見つけることをします。それをコストに足し込むことで全体のコスト値をシフトさせます。
そうすると、もしコスト値が超えていたら、cよりも上位の量子ビットのどこかが1になっているはずです。逆にコストを超えていないなら、cよりも上位の量子ビットは全て0になっています。そこで、cよりも上位の量子ビットのみを対象に、一度全部XゲートかけてMCTゲートを作用させることで、閾値を超えていないなら全て1になっているはずなので、MCTゲートが作用してフラグの値を反転させます。閾値を超えていないなら、MCTゲートが作用しないので、フラグの値はそのままになります。後は、フラグをこの処理の前後で反転させておけば、閾値を超えていないなら0、超えていたら1にセットすることができます。
このアイデアを説明しているのがこの部分です。

def constraint_testing(data_qubits: int, C_max: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_data = QuantumRegister(data_qubits, "data")
qr_f = QuantumRegister(1, "flag")
qc = QuantumCircuit(qr_data, qr_f)
##############################
### Set the flag register for indices with costs larger than C_max ###
# Put your implementation here
N=2**data_qubits
#次に上位の閾値までの差分(diff)を計算
if 2**math.ceil(math.log(C_max,2)) == C_max:
diff = 2**math.ceil(math.log(C_max,2))*2 - C_max - 1
threshold = math.ceil(math.log(C_max,2)) + 1
else:
diff = 2**math.ceil(math.log(C_max,2)) - C_max - 1
threshold = math.ceil(math.log(C_max,2))
# データqubitにdiffを足し込み、閾値を2^cに揃える。ただし、diffが0(C_max=2^c-1のとき)なら何もしないようにして不要なゲートは作らないようにする
if diff > 0:
for d in range(data_qubits):
qc.u1(2*math.pi*diff*(2**d)/N,qr_data[d])
# 全てのフラグを一度1にセット
qc.x(qr_f[0])
# 逆QFTによって位相の肩に乗っている値を計算基底状態にエンコード
iqft = QFT(data_qubits,inverse=True)
iqft = transpile(iqft, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
qc.append(iqft.to_gate(label='IQFT'),qr_data[:])
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
# 2^cよりも大きい量子ビットを一度反転させて、コスト+diff<=2^cではフラグを反転させて0にする。逆にコスト+diff>2^cではフラグは1のままにする
qc.x(qr_data[threshold:])
qc.mct(qr_data[threshold:],qr_f)#,ancilla_qubits=qr_tmp[:],mode='recursion') # 補助ビットを使ってmctを最適化しようしたしたが効果なし。
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
return qc.to_gate(label=" Constraint Testing ") if to_gate else qc
step5 ペナルティの位相緩和
この問題の2つの山場は無事クリアしました。後は一本道です。
次にはペナルティの位相緩和ですが、やっていることは、フラグが1なら、利益にペナルティを付与することです。今回はペナルティは、閾値からオーバーした分としています。
やることは単純で、フラグ量子ビットを制御量子ビットとして、CUゲートを利用します。こうするとことで、フラグが1なら、ペナルティが与えられます。
まとめると次のような構成になります。

あれ?さっき適当な値でコスト値をシフトさせてたから、それそのまんま使ったらまずくない?利益の計算間違えるのでは?という疑問が出てくると思います。それは心配しなくてもよく、それを閾値をシフトさせた分、コストもシフトしているわけで、それに合わせてペナルティを与えるのには特別工夫はいらないです。そのまま、シフトさせた状態でペナルティを与えていけるのは、コスト値を2進数で表現してみると、簡単な数式でチェックできます。
以上をコードにしたのが以下です。
def penalty_dephasing(data_qubits: int, alpha: float, gamma: float, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_data = QuantumRegister(data_qubits, "data")
qr_f = QuantumRegister(1, "flag")
qc = QuantumCircuit(qr_data, qr_f)
##############################
### Phase Rotation ###
# Put your implementation here
N = 1
for i in range(data_qubits):
qc.cu1(alpha*gamma*N,qr_f[0],qr_data[i])
N*=2
qc.u1(-alpha*gamma*(2**math.ceil(math.log(C_max,2))) ,qr_f[0])
##############################
qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
return qc.to_gate(label=" Penalty Dephasing ") if to_gate else qc
step6 再初期化
再初期化はstep2~5までの処理を逆にたどって、元に戻す操作です。
え?今までのを逆順に書くの?無理じゃね?と思うかもしれません。
ご安心ください。そういったこともあろうかと、Qiskitにはinverse()関数が用意されているので、これを使えば、どんなに長い回路でも逆順にしたものを用意してくれるのです!!!
ここまでに作った回路は関数化してあるので、それを使って順序通りの回路を作ってから、inverse()をかますことで、逆順が用意されます!以下のようになります。
def reinitialization(index_qubits: int, data_qubits: int, C1: list, C2: list, C_max: int, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qr_data = QuantumRegister(data_qubits, "data")
qr_f = QuantumRegister(1, "flag")
qc = QuantumCircuit(qr_index, qr_data, qr_f)
##############################
### Reinitialization Circuit ###
# Put your implementation here
qc.append(cost_calculation(index_qubits,data_qubits,C1,C2),qr_index[:]+qr_data[:])
qc.append(constraint_testing(data_qubits,C_max),qr_data[:]+qr_f[:])
qc = qc.inverse()
#qc = transpile(qc, backend=Aer.get_backend('aer_simulator'), seed_transpiler=1234, optimization_level=3)
##############################
return qc.to_gate(label=" Reinitialization ") if to_gate else qc
step7 ミキシング
最後はミキシングという操作ですが、これはQAOA固有の処理になります。あまり悩まず、そのまま誘導になりましょう。
def mixing_operator(index_qubits: int, beta: float, to_gate = True) -> Union[Gate, QuantumCircuit]:
qr_index = QuantumRegister(index_qubits, "index")
qc = QuantumCircuit(qr_index)
##############################
### Mixing Operator ###
# Put your implementation here
if beta > 0:
qc.rx(2*beta,qr_index)
##############################
return qc.to_gate(label=" Mixing Operator ") if to_gate else qc
ここまで書けば、後は用意されているものを実行することで、計算が走ります。最終版は一番最初に書いたコードになります。
著者の結果
最終的には、366560というスコアで15位という結果でした。
基本的には著者としては誘導通りに愚直に書いていき、愚直な処理をなるべく簡便な処理に置き換えるなどしてスコアを下ました。決して奇をてらっていない流れになっているかと思います。そういう意味でサンプルコードとしても、なかなか良いのではないかと自負しています。
なお、トップ10の上位陣はunder 300000なので、この奇をてらっていない状態から、もう少し工夫の余地があるという所です。
https://github.com/qiskit-community/ibm-quantum-challenge-fall-2021/tree/main/topscorers
上位陣の更なる工夫
上位陣のをいくつか見ていると、著者の解答に比べて以下のような工夫が見受けられます。
・コスト計算でのコスト加算処理で不要なゲートを削除する
・逆QFTを真面目に使うのではなく、あえて正解の精度を犠牲にして、より簡単な回路で組み直す
最上位の人は、この精度を犠牲にして、最終結果に対する影響の小さい”枝葉の値”を切るという工夫でさらにスコアを圧縮しているようです。今回の問題が必ずもピッタリと正解状態が100%観測される必要はないので、枝葉の値を切ったとしても正解と判定されるように微調整を加えたようです。
このアイデアは、IoT/EdgeAI的にも使われて、ディープラーニングモデルを軽量化するアイデアに似ています。つまり、スペックの低いマシンでも高スペックのマシンに近い精度と速度を出せるような工夫に通じています。アイデアは以下のようなものです。https://laboro.ai/activity/column/engineer/%E3%83%87%E3%82%A3%E3%83%BC%E3%83%97%E3%83%A9%E3%83%BC%E3%83%8B%E3%83%B3%E3%82%B0%E3%82%92%E8%BB%BD%E9%87%8F%E5%8C%96%E3%81%99%E3%82%8B%E3%83%A2%E3%83%87%E3%83%AB%E5%9C%A7%E7%B8%AE/
著者も本業などでEdgeAI周りをやっているので、軽量化はもともと知っているアイデアではありましたが、その着想はここでは出なかったので、読んでていて大変勉強になりました。
最後に
今回も自力で最後まで解ききれたので、大変満足です。当時の自分ができる限界には到達できたとは思います。次があれば10位以内を目指して頑張ってみたいと思います。
この問題って古典で解けないの?
今回の問題は量子で解きましたが、Challengeが終わってから、「このケースって古典じゃ解けないのだっけ?」と疑問が出てきました。
そこで、弊社の数理最適化の御大である、とある技術理事にご教示頂いたところによると、古典でも解けるとのことで、スラック変数というのを導入して、制約条件と目的関数の両方にその変数を組み込んで定式化するようです。なので、これは量子固有で解ける問題ではなかったということになります。そういった意味でも勉強になりました。
余談
実は、Challenge終了時刻12時間ぐらい前に、やっとの思いで100万台のスコアを出せて25位くらいにつけて、そのまま満足しちゃって仕事して終わった後にサウナ屋に行っていたのですが、終了3時間前にサウナ屋のお風呂に入った瞬間に100万台→30万台に至るアイデアがひらめき、風呂から飛び出して、休憩室ですぐにコードを書き直して、15位に順位を上げましたw
教訓としては、煮詰まったら散歩するなり、風呂に入るなりして、環境を変えると閃きが生まれるかもしれないってことですw