ロジスティック写像の時系列
ロジスティック写像とは以下で表される1次元写像のことである。
パラメータaの値が大きくなると軌道がカオスになることで有名である。
f(x) = x_{n+1} = ax_n(1-x_n)\\
(0 \le a \le4)
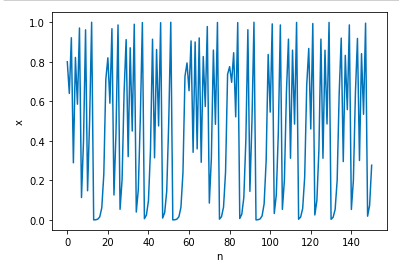
横軸をn(ステップ数150回とする)、縦軸を x として、x の時系列を求めたい。(a = 4 のとき)
今回はロジスティック写像の時系列のプログラムを詳しく説明する。
時系列を折れ線グラフで表す
import matplotlib.pyplot as plt
x = [0.8]
a = 4.0
n = [0]
for i in range(1,151):
x.append(a * x[-1] * (1 - x[-1]))
n.append(i)
plt.plot(n,x)
plt.xlabel("n")
plt.ylabel("x")
plt.show()
解説
⒈ グラフを作成するために必要なライブラリをインポート
import matplotlib.pyplot as plt
⒉ 初期値を設定
最後にグラフにするときにxのリストとnのリストの値の数が同じになるようにステップnの初期値も、n=[0]を入れておく。
a = 4.0
x = [0.8]
n = [0]
⒊ for文で150回繰り返し
appendでxとnのリストの中に150個の値を追加する。
ここで、初期値n=[0]がもともと入っているため、nのリストには1から追加できるようにrange(1,151)で、1から150回繰り返せるようにする。
それにより、for文の中のxはx[i]と表現してしまうと、for文の1回目の実行でx[1]がありませんというエラーが出てしまうため、x[-1]という表現にする。(これはxのリストの中で一番右にある値を表す。)
for i in range(1,151):
x.append(a * x[-1] * (1 - x[-1]))
n.append(i)
⒋ グラフを出力
plt.plot(n,x)
plt.xlabel("n")
plt.ylabel("x")
plt.show()
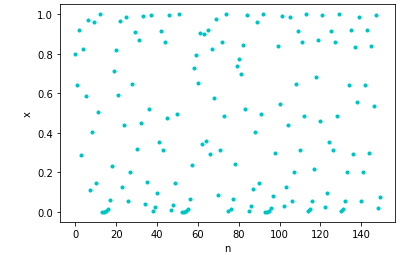
散布図
ちなみにfor分の中でplt.plotをすると以下のような散布図になってしまうので注意
import matplotlib.pyplot as plt
a = 4.0
x = [0.8]
for i in range(150):
x.append(a * x[i] * (1 - x[i]))
plt.plot(n, x[i], "c.")
plt.xlabel("n")
plt.ylabel("x")
plt.show()
パラメータaの値を変えると、固定点に収束したり周期点に収束したりなど様々な振る舞いをすることが分かる。