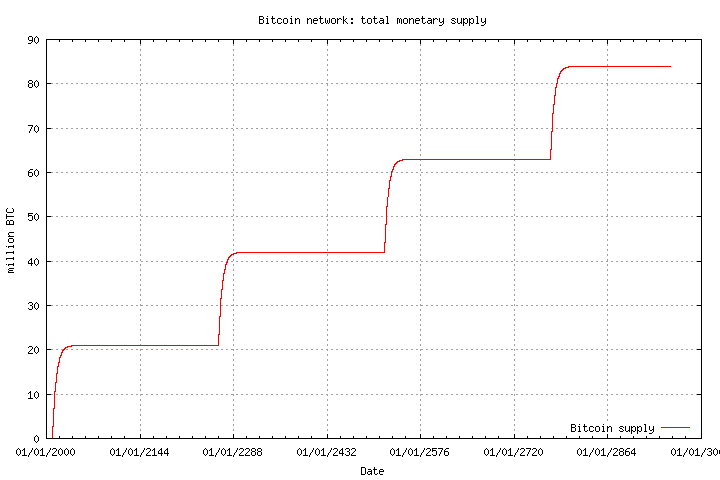
みなさんご存知の通り、Bitcoinの発行量はあらかじめ決まっています。
つまり、発行量がその値に達するとそれ以上新しいコインは発行されなくなります。
もう少し詳しく言うと、新しく発行されるBitcoinの量がおよそ4年ごとに半減していき、最終的に0になるためそれ以上発行されなくなります。
発行量を制御しているコード
その辺を制御しているコードがこちらです。
int64_t nSubsidy = 50 * COIN;
nSubsidy >>= (nHeight / 210000);
簡単に解説をします。
まず最初の行で、nSubsidyを初期化しています。
subsidyは補助金や交付金という意味合いなので、nSubsidyはnumber of subsidy、つまり交付金の量という意味です。
これはブロック毎に新しく発行されるBTCの量を表しています。
COINは100000000とdefineされており、これは1BTCあたりのsatoshiの量です。
つまり初期化時のnSubsidyの値は50BTCとなります。
次のコードは、nSubsidyをbitshiftしています。
低レベルな言語ではよく、「2で割る」という演算を「右にbitshiftする」という演算で置き換えます。
右に1bit bitshiftすると1/2になり、2bit bitshiftすると1/4になります。
そして何bit bitshiftするかを決めているのが、(nHeight / 210000)の部分です。
つまり、nHeightが0~209999のときは0bit bitshift、210000~419999のときは1bit bitshiftすることになります。
nHeightが大きくなるたびに、nSubsidyが半減していくのが1行で表されています。
お分りいただけただろうか
さて、たった2行で発行量の制御を実現しているカッコいいコードですが、このコードに潜むバグに気がつかれた方はいるでしょうか。
気がつかなかった人はもう一度、例のコードを見てみましょう。
ヒント
上記のコードのどこにバグが潜んでいるのか。
答えは2行目です。
nSubsidy >== (nHeight / 210000);
どうでしょう。気がつきましたか?
解説
では解説をしていきます。
nHeightが大きくなっていくと、シフトする量は、0, 1, 2,,,と大きくなっていきます。
では、 シフト量がnSubsidyのbit長よりも大きくなったらどうなるのでしょうか。
1行目を見ると、nSubsidyのbit長は64であることがわかります。
64bitで表現されている値を100bit分シフトしたりしたらどうなるのでしょうか。
その答えは、未定義 です。
未定義ということは、
「64を超えたら何があろうと0になるぜ!」みたいなコンパイラも、
「100を64で割った余りの36bitだけシフトするぜ!」みたいなコンパイラもありえるということです。
そして2つめのようなコンパイラでは、Bitcoinの発行量は以下のようになります。
つまり発行量無限ですね。
タネ明かし
実はこのバグはSatoshi Nakamotoのオリジナル実装にあったバグで、2014年に修正されています。
現在の実装では、(nHeight / 210000)が64を越えると、シフト量が0になるようになっています。
これでBTCの総発行量はちゃんと有限ですね。
タイトルは、「(Satoshi Nakamotoのオリジナル実装の)Bitcoinの発行量は無限!?」という意味でした。