はじめに
はじめまして.株式会社音圧爆上げくんにプロKagglerとして所属していますAshmeと申します.
業務の一環としてKaggleの様々なコンペティションに参加し,そこで得られた知見などを記事にして投稿しております.よろしくお願いいたします.
今回は現在のKaggleコンペティションに直接関係のあるものではありません.Twitterで流れてきたものですが教師なし特徴量選択の手法であるFRUFS(Feature Relevance based Unsupervised Feature Selection)という手法に興味があったのと,コンペティションで特徴量選択の1つとして使用することもできると考えたためこちらについて紹介します.
こちらの手法はDeepwizAIにて紹介されていた手法です.元の記事はこちらにありますので,興味がある方はぜひこちらを読んでみてください.
本記事ではこのFRUFSと通常の教師あり学習における特徴量選択の違い,FRUFSはどのような考え方に基づいた手法なのか,どのように実装するのかについて紹介していきます.
教師あり学習における特徴量選択
まずこれまでもよく用いられてきた教師あり学習における特徴量選択について説明します.教師あり学習での特徴量選択は主に3種類に分類され,フィルター法,ラッパー法,埋め込み法が存在します.まずはこれらの3つの手法について簡単に説明していきます.
フィルター法
フィルター法は特徴量選択の中で一番コストが低い手法だと思います.これは統計的な考え方に基づいて重要な特徴量を選択する手法です.例えば多重共線性という言葉を聞いたことがあるのではないでしょうか.相関係数が高い特徴量があると学習の結果が悪くなるということを聞いたことがあると思います.そこでEDAなどの早い段階で各特徴量間の相関係数を計算し,相関が大きい特徴量に関しては片方を不要として学習に用いないとする方法があります.ただこの多重共線性においては機械学習では予測精度を高くすることを目的とするため,そこまで深く考えないこともあるそうです.多重共線性につきましては調べれば簡単に出てきますので興味のある方は調べてみてください.
ラッパー法
ラッパー法と埋め込み法は機械学習モデルを学習させることで特徴量選択を行いますが,それぞれ方法が少し異なります.ラッパー法は使用する特徴量を徐々に増やす,もしくは少なくすることで特徴量選択をします.徐々に増やす場合は使用する特徴量を1つ増やしたときに最もスコアが増加する特徴量を追加するということを繰り返します.逆に少なくしていく場合は使用する特徴量を1つ減らしたときに最もスコアが減少しない特徴量を削除するということを繰り返します.使用する特徴量の数を事前にしてしておき,その数に達したら処理を終了します.
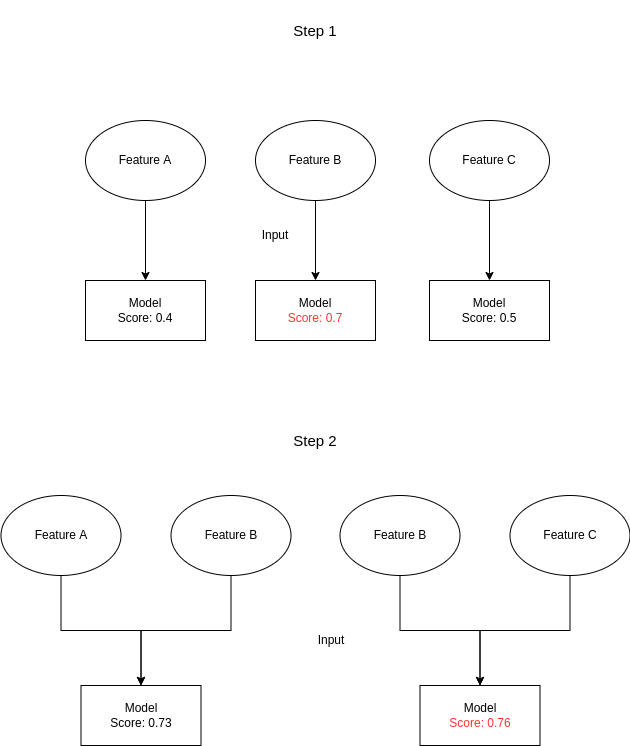
文字だけでは少し分かりづらいため,簡単な例を図にしてみました.例は使用する特徴量を増やす場合です.ほとんど意味はないですが,もともと特徴量が3つのものを2つにしたいと考えます.今回の性能はAccuracyを仮定し1に近いほど良いとします.
Step1では3つの特徴量を1つずつ入力してモデルを学習し性能を評価します.この場合,Feature Bが最も性能が高いためFeature Bは1つ目の特徴量として使用することが決まります.
Step2で2つ目の特徴量を決めます.このときStep1で最も性能が高かったFeature Bは必ず用いることにし,Feature AとFeature Bを入力した場合とFeature BとFeature Cを入力としてモデルを学習し性能を評価します.結果としてFeature BとFeature Cを入力としたほうが性能が良いためこの2つを特徴量として使用することが決まります.
今回の場合は使用する特徴量は2つにすればよいためここで終了となります.例えば100個の特徴量を50個にしたい場合はこれを特徴量が50個決まるまで繰り返します.
この手法の考え方としては最もスコアが増加する特徴量は残っている特徴量の中で予測するのに最も重要である,最もスコアが減少しない特徴量は特徴量の中で予測に最も重要でないという考えに基づいていると考えられます.この手法は機械学習のどの手法でも利用することができますが,何度もモデルを学習するためコストがかかってしまいます.ただし使用するモデルに対して最も良い特徴量の組み合わせを得ることができます.
埋め込み法
埋め込み法はラッパー法と同様に機械学習モデルを学習させることで特徴量選択を行いますが,こちらは学習は1度のみになります.ただし,使用できるモデルが限られており,線形回帰モデルかXGBoostやLightGBMなどのGBDTを用いることができます.線形回帰モデルではモデル学習した後に,各特徴量の重みを重要度と考え,重みの絶対値が大きいものほどその特徴量の重要度が高いとします.またGBDT系のFeature Importanceは大きいものほど重要な特徴量としています.本記事で紹介するFRUFSはこの埋め込み法の考え方に近いです.
また実際の予測にこれら以外のモデルを使用する場合は,上記のモデルで重要度が高い特徴量を選択し,それらの特徴量を用いてモデルを学習することができます.
本題とは外れますが,特徴量の重要度の考え方は,上記のようなものだけでなく局所的な近似モデルを再現することで解釈を可能にするLIMEや,ゲーム理論におけるシャープレイ値の考え方を用いるSHAPという手法も存在します.また画像に関してもGrad-Cam,系列データに対してはTransformerに用いられているAttentionによってどの時間の特徴量が重要なのかを知ることができるなど様々な手法が提案されています.これらを知っておくとモデルがどの特徴量に注目して予測しているかの解釈を得ることができるため興味ある方は調べてみると良いと思います.
FRUFS
教師なし学習での特徴量選択
教師あり学習での特徴量選択法について知ることができたので,本題であるFRUFSに入っていきたいと思います.FRUFSの紹介については元の記事の順序に基づいて紹介していきたいと思います.
FRUFSの考え方に似ているものは埋め込み法です.まず埋め込み法を線形回帰モデルで学習したときのことを考えてみます.線形回帰モデルを定式化すると以下のようになっています.線形回帰モデルで特徴量重要度を理解する際にバイアス(切片)は不要なため式から除いています.
$$\hat{y} = \alpha_1 x_1 + \cdots + \alpha_D x_D = \sum_{d=1}^D \alpha_d x_d$$
$\hat{y}$はモデルの予測値,$\alpha_d$はd番目の特徴量に対する重み,$x_d$はd番目の入力を表しています.また入力次元はDとしています.このとき重み$\alpha_d$はd番目の特徴量が予測をするためにどれだけ寄与しているか,重要であるかを表していると考えることができます.教師なし学習では正解ラベルがないため同様の手法を用いることができません.そこで予測するものを正解ラベルではなく,他の入力特徴量に置き換えます.上記と同様に式にすると以下のようになります.
$$x_k = \sum_{d \neq k}^D \alpha_d x_d$$
つまりk番目の特徴量をそれ以外の特徴量で表現するということになります.
これを用いてどのように特徴量の重要度を考えるのかと言うことについて説明します.
例として1番目の特徴量に焦点を当てて他の特徴量,つまり1番目以外の特徴量を表すときのことを考えます.
まずk番目の特徴量を表すときにj番目の特徴量にかけられる重みを$w_{jk}$とします.このとき1番目の特徴量について,2番目の特徴量を表すときの重み$w_{12}$,3番目の特徴量を表すときの重み$w_{13}$…というように1番目の特徴量に対してかけられる重みはD-1個存在します.この重みの平均が大きいほどその特徴量の重要度が大きいと考えます.上の式を今定義した$w_{jk}$を用いて書き直すと以下のようになります.
$$x_k = \sum_{j \neq k}^D w_{jk}x_j$$
なぜなら$w_{jk}$はk番目の特徴量を表すときにj番目の特徴量をどれだけ重要とされているかを表しているためです.j番目の特徴量が他の特徴量を表すときに重要とされているということは,他の特徴量の情報をj番目の特徴量が多く含んでいると考えられます.したがって入力データ全体を入力データの一部の特徴量(重要度が大きい特徴量)で表現できるということになります.
この考え方は他の式を見ると少しわかりやすいかと思います.上記の重みは以下のように決定されます.このとき入力データの計画行列を$X(N \times D)$,重み行列を$W(D \times D)$としており,$W_{kj}$はj番目の特徴量を表すときのk番目の特徴量の重みを表しています.つまりj列目にはj番目の特徴量にかける重みが並んでいることになります.また$W$の対角成分はすべて0になります.これはj番目の特徴量を表すのにj番目の特徴量を用いないためです.
$$X = XW^T$$
$$X - XW^T = 0$$
上記の式を完全に満たすことはほぼできないため,結果としては$X - XW^T$のフロベニウスノルム(行列の各要素の2乗和の平方根)を最小化することになると元の記事にはありますが,簡単に言えば元の入力データともとの入力データに$W^T$をかけて作成したデータの各要素の差が0に近づくようになればよいということであり,$XW^T$によって元データ$X$をできる限り表現できれば良いということです.
ここで扱った線形回帰モデルを用いての教師なし学習での特徴量選択はすでに2015年の研究論文で発表されているようです[1].
これを元にFRUFSは少し手を加えたものになっています.
FRUFSと前節の手法の違い
ではFRUFSでは前節の手法と何が異なるのでしょうか?これは非常に単純なもので,線形モデルの代わりに非線形モデルを用いるという部分だけです.ここでいう非線形モデルとしてLightGBMを扱っています.線形モデルでは特徴量の重要度として各特徴量に対する重みを持ちていました.その代わりにGBDT系で計算することができるFeature Importancesを用いることになります.なのでおそらくですがLightGBMでなくXGBoostやCatBoostなどの特徴量重要度を計算できるモデルであれば用いることができると考えられます.
FRUFSの実装
FRUFSをMNISTデータセットに対して適用したものが元の記事で実装されていますが,私自身でも実装してみました.そこまで難しい実装ではないためみなさんも一度実装してみると良いと思います.私が実装の全体(FRUFSの実装以外は結果を比較したいため同じです)はこちらにありますが,元の記事では並列処理をうまく使用していたりするため,元の記事のものを参考にするほうが良いと思います.
私の実装ではPandasのDataFrameを入力し,メソッドを呼び出すことで重要度の計算,可視化ができるようにクラス化しています.また比較用に線形モデルとLightGBMのどちらも利用できるようにしています.
# 他の特徴量を計算するための重み/重要度を計算する
def calc_coef(self):
X = self.df.values
for i in tqdm(range(X.shape[1]), total=X.shape[1],
desc="calculate coefficient/importances"):
# 重み/重要度を格納するインデックスの指定
indices = np.concatenate((np.arange(i).reshape(-1, 1),
np.arange(i+1, X.shape[1]).reshape(-1, 1)))
train_X = np.hstack((X[:, :i], X[:, i+1:])) # i番目の特徴量を外す
train_y = X[:, i] # i番目の特徴量
# i番目の特徴量を他の特徴量で表現するための学習
model = self.model_func()
model.fit(train_X, train_y)
# モデルの重み/重要度をWに格納する
if self.method == "linear":
coef = model.coef_
coef = np.absolute(coef)
elif self.method == "lgb":
coef = model.feature_importances_
self.W[i, indices] = coef.reshape(-1, 1)
# 各特徴量が他の特徴量を表すときの重み/重要度の平均を計算
self.W_average = self.W.mean(axis=0) # 列方向に平均を取る = ある特徴量にかけられる重みの平均
self.average_coef_df = pd.DataFrame({"columns": self.df.columns.values,
"importances": self.W_average})
実際にある特徴量を他の特徴量を用いて表現するときの特徴量重要度を計算し,データを保存する部分になります.実装の中でインデックスの部分が少し分かりづらいかと思うので説明します.
# 重み/重要度を格納するインデックスの指定
indices = np.concatenate((np.arange(i).reshape(-1, 1),
np.arange(i+1, X.shape[1]).reshape(-1, 1)))
train_X = np.hstack((X[:, :i], X[:, i+1:])) # i番目の特徴量を外す
train_y = X[:, i] # i番目の特徴量
この辺の部分は配列を扱う機会があればわかりやすいかと思いますが,あまりない方向けに説明します.ここには載っていませんが,重み$W$をインスタンスの初期化のときに作成しています.このとき$W$は説明の通り$D \times D$のゼロ行列として初期化しています.j列目はj番目の特徴量が他の特徴量を表現するときにかけられる重みが並んでいますが,k行目にはk番目の特徴量を表すときにk番目の特徴量以外にかける重みが並んでいます.
特徴量重要度の計算はk番目の特徴量を計算するときのそれ以外の特徴量重要度を得ることになるため,結果をk行名に格納することになります.またこのときk行k列目は0である必要があるためk番目はindicesに含まないようにしています.
そして入力データとしてk番目以外の特徴量,出力の教師ラベルとしてk番目の特徴量をそれぞれtrain_X, train_yとしています.これを用いてモデルを学習させることになります.
結果
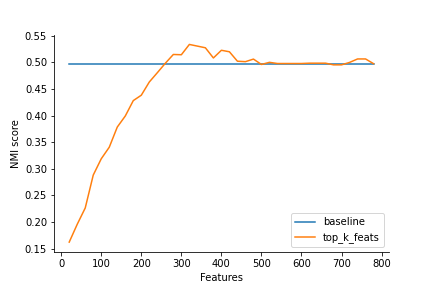
元の記事と同様の可視化やスコアの算出をしたところ以下のようになりました.データのとり方が少し異なっている(私の場合はscikit-learnを用いている),データの一部を用いており再現性確保をしていないため,多少結果がぶれますが,元の記事の実装とほとんど遜色ない結果を得ることができました.論文実装など様々なものがありますが,そういうものに慣れていない方でもこちらの実装はわかりやすいと思うので練習と思って一度実装してみると良いと思います.
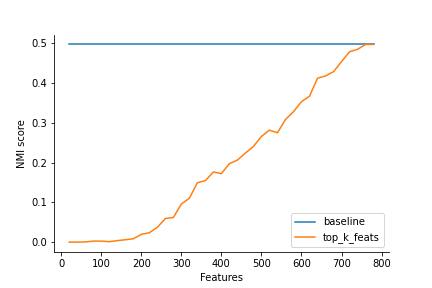
また比較用に線形モデルでの結果も載せておきます.こちらの結果だと特徴量すべてを用いたものが最もスコアが高いということでうまく特徴量選択できていないことが解ると思います.ただ流石に悪すぎる気もするので実装を一度見直してみようと思います.
おわりに
今回は現在開催されているコンペティションに直接関係はしていませんが,教師なし学習での特徴量選択手法FRUFSについて紹介しました.結果を見ても教師なし学習のコンペティションのときに特徴量選択として使用できる可能性もあるのではないでしょうか.また教師あり学習のときにこの手法で特徴量選択をしてもすべての特徴量より良い性能を示すこともあるそうなので使用してみようと思っています.
最後に人材募集となりますが,株式会社音圧爆上げくんではプロKagglerを募集しています.
少しでも興味の有る方はぜひ以下のリンクをご覧の上ご応募ください.
Wantedlyリンク
参考
[1] Zhu, Pengfei, Wangmeng Zuo, Lei Zhang, Qinghua Hu, and Simon CK Shiu. "Unsupervised feature selection by regularized self-representation." Pattern Recognition 48, no. 2 (2015): 438-446.