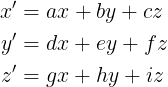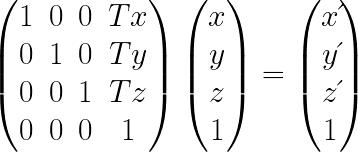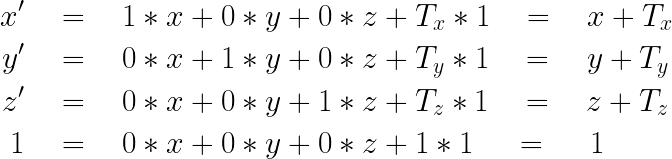WebGL 学習①

WebGLとは

WebGL はウェブブラウザ上での3Dグラフィックスの描画やGPUコンピューティングを実現するためのAPI。

JavaScriptとHTML5を組み合わせて使用し、Webページ上でリアルタイムの3Dグラフィックスを表示して、操作する事ができる。

ブラウザ上で動作するプログラムであるため、特定のプラットフォーム（OS）には依存せずにWebページ上で3Dグラフィックスを表示させることができる。

• Khronos Group によって仕様が策定される
• WebGLは「OpenGL ES (Open Graphics Library for Embedded Systems)」のブラウザ版として位置付けられている
• OpenGL ESとは組み込み機器向けの2D / 3DCG描画ライブラリであり、WebGLはそのサブセットとして定義されている
• 異なるバージョンの OpenGL ES同士は互換性はないためWebGLを使用する場合には、特定のバージョンに準拠する必要がある
• HTML5の<canvas>要素などと組み合わせて使用する
• 並列処理に特化しているGPU上で動作するため、高速な3D描画や計算を行う事ができる

Canvas

<canvas>タグによってWebページ上に描画領域を確保して、JavaScriptによって色、形などの指定を行う。

<canvas id="target" width="100" height="100"></canvas>

JavaScriptでの基本的な描画
1. コンテキストを取得する
2. パス作成を開始する
3. 描画開始位置に移動する
4. パスを生成する
5. パス作成を終了する
6. パスを描画する

canvasの座標

HTML

<canvas id="target" width="1000" height="1000"></canvas>
<script src="main.js"></script>

JavaScript

const canvas = document.getElementById('target');
if (!canvas || !canvas.getContext) {
    // キャンバスに未対応の場合
    console.log('ブラウザが対応していません');
}
let ctx = null;
ctx = canvas.getContext('2d');  // コンテキストを取得する
ctx.lineWidth = 10;  // 線の幅
ctx.storokeStyle = "black";  // 線のスタイル
ctx.beginPath();  // パス作成を開始する
ctx.moveTo(100, 100);  // 描画開始位置に移動する
ctx.lineTo(200, 200);  // パスを生成する
ctx.closePath();  // パス作成を終了する
ctx.stroke();  // パスを描画する

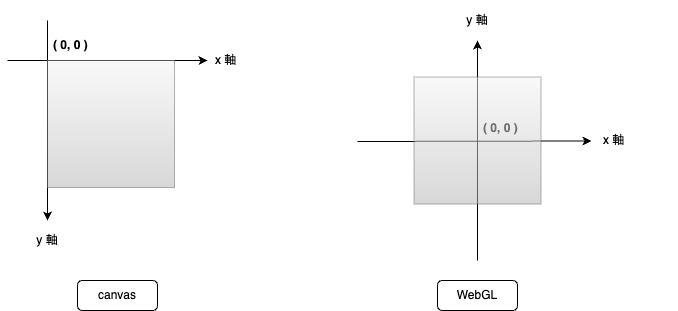
注意：canavsとWebGLの座標系は、原点の位置、軸の向きが異なる

WebGLでは正面から見たときに右がx軸の正方向、上がy軸の正方向、奥から手前がz軸の正方向

必要な数学的知識

ラジアン（Radian）

ラジアンは角度を表す単位の一つであり、円の弧の長さと、半径の比率に基づいて定義される。円の弧の長さは円周上の一部を指し、半径は円の中心から円周までの距離を指す。ラジアンの定義は、半径が1の円の円周上の弧の長さが1ラジアンであるというもの。

半径が１の円の円周上の長さは２π（直径 × π）なので、半径が１の円の円周上の孤の長さが１ラジアンということは、１ラジアンは２πという値になる。また、円の周囲は３６０度で表現される。したがって、円孤１周分の長さ（３６０度分）は2πラジアンになる。

ラジアンは度数法と比較して、数学や物理学、工学の分野でよく利用される。ラジアンを利用すると、三角関数の公式や関係がシンプルに表現できるため、複雑な計算が簡単になる。

ラジアンと度数法は相互に変換する事ができる。

半径が１の円の円周上の孤の長さが１ラジアン（rad）
→ ラジアン（rad）　＝　孤の長さ　÷　円の半径

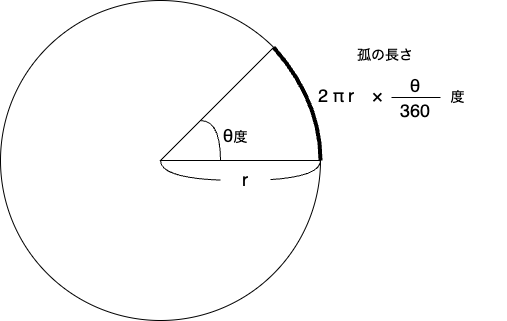
半径がrの円の円周は2πr。
角度がθ度の扇型の弧の長さは2πr ×　θ　÷　360。
つまり、
ラジアン　＝　　　弧の長さ　　　　　　 ÷　　　　　円の半径
　　　　　＝　2πr　×　θ　÷　360　　　÷　　　　　　　r
　　　　　＝　θ　×　π　÷　180

例えば、角度30度は、（30　×　π　÷　180）ラジアンとなる。

ベクトル（Vector）・行列（Matrix）

ベクトル（Vector）は「値（スカラー値）」と「方向」を持つ量を表すもの。スカラーと対比される概念。

スカラーは方向に関する情報を持たない。例えば、実数や整数などはスカラー値として扱われる。そのため、１次元のベクトルはスカラーと同等と言えるかもしれないが、ベクトルは複数の次元を持つことができる。２次元のベクトルはx軸とy軸から構成される。

（x, y, z）という三次元のベクトルは、一つ目の要素がX「方向」に関する「値」であるx、二つ目がY方向の値y、三つ目がZ方向の値zを保持している。

行列（Matrix）は、数値の配列を表すもの。

「行」と「列」から構成される。行列の１要素には、スカラー値が格納されている。行列はベクトルや、多次元のデータを格納したり、表現するのに適しており、加算、減算、乗算などを行うことができる。

ベクトルと行列は、コンピュータグラフィックスや、3Dグラフィックスの分野において、3Dオブジェクトの位置や向き、変換、光の計算、カメラの移動などに広く使用される。

WebGLにおいては、主に行列の乗算がよく利用される。行列の演算では、２つの行列を組み合わせて新しい行列が生成される。行列の乗算は、掛け合わせる行列同士の列の要素数が一致している必要がある。行の数は一致している必要はないため、行列に対して、列方向の要素数が同じベクトルを掛け合わせることもできる。

　　 　　

WebGLでは行列を配列で扱うが、行優先の行列（Row-Major Matrix）、列優先の行列（Column-Major Matrix）のうち列優先の行列として扱う点に注意する。上の行列を列優先の行列で表現すると、[a, d, g, b, e, h, c, f, i]となる。

WebGLでは行列は列優先の行列として扱う

座標変換行列（Transformation Matrix）

3Dグラフィックスにおいて、オブジェクトの移動、回転、スケーリングなどの変換を行うために使われる行列。3D空間上の点やベクトルを別の座標系に変換することができる。回転行列や平行移動行列、拡大縮小行列などがある。

回転行列（rotation matrix）

3Dオブジェクトを回転させる為の行列。左から、X軸周り、Y軸周り、Z軸周りの回転行列。これらを回転前のベクトルに掛け合わせることで、回転後のベクトルを取得する事ができる。
        
ここで、理解を深めるためにZ軸周りの回転行列を検証してみる。

座標では点A（x, y, z）から点B（x', y', z'）へ回転するとする。平面（２次元）での回転になってしまうが、点BはZ軸（奥から手前方向）周りに点Aから角度 β ラジアンだけ回転しているとする。

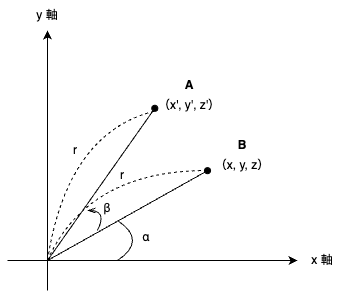
図形を回転させるためには、３つの情報が必要。

• 回転の軸（X or Y or Z）
• 回転の方向（正 or 負）
• 回転する角度（単位はラジアン）

今回の回転では以下のようになる。

• 回転の軸（Z）
• 回転の方向（正）
• 回転する角度（β）

※軸と方向を覚えるには、「右手で」親指を立てて、いわゆる「グッド👍」の形を作る。親指の根本から先端に向けてが軸の正方向とした場合、親指以外の根本から先端に向かう方向が回転の正方向。（右手形の回転と呼ばれる）

ただし、クリップ座標は右手形の座標であるので注意する

回転行列を使用すると、回転後のベクトルは以下のようになる。

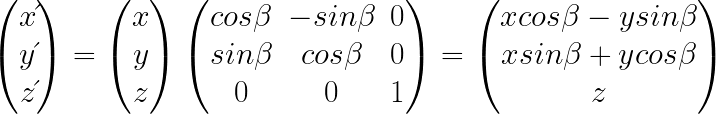
この回転後のベクトルを、回転行列を使用せずに求めてみる。

まず、回転前の座標A（x, y, z）を原点からの距離 r とX軸からの角度 α で表現する。
    
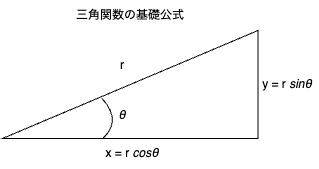
x = r cos α　　　・・・①
y = r sin α　　　・・・②

回転後の座標B（x', y', z'）を原点からの距離 r とx軸からの角度 α で表現し、さらに、三角関数の加法定理を使用して式を変換する。
x' = r cos（ α + β ） = r （ cos α cos β - sin α sin β ）　・・・③
y' = r sin（ α + β ） = r （ sin α cos β + cos α sin β ）　・・・④

①②から sin α 、cos α を得る。
cos α = x / r　　　・・・①'
sin α = y / r　　　・・・②'

①'②'を③④へ代入する。
x' = r（cos α cos β - sin α sin β ） = x cos β - y sin β
y' = r（sin α cos β + cos α sin β ） = y cos β + x sin β

確かに回転行列を掛け合わせると、回転後のベクトルを得る事ができる事がわかる。

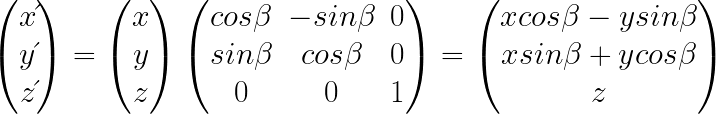
後述する平行移動行列が４要素であるため、実際には４要素に拡張して使用される。左からx軸周り、y軸周り、z軸周りの回転行列。座標系を拡張する手法は同次座標系と呼ばれる。
        

平行移動行列（Translation Matrix）

3Dオブジェクトを指定した距離と方向に平行移動させる為の行列。

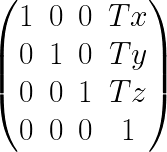
（Tx, Ty, Tz）が移動距離を表すベクトル。ベクトルに対して平行移動行列を掛け合わせることで、移動後の新たなベクトルを得ることができる。

3次元空間において、ベクトルは3要素のはずが、平行移動行列では4要素になっている。これは行列を用いて計算を行うための偉人が考えたテクニックなので、「うまく計算する方法」と捉える。

まず、平行移動行列の計算において、ベクトル（x, y, z）は（x, y, z, 1）の4要素に拡張する必要がある。この時４番目の要素「１」は行列の計算に必要なだけで、座標系において何かの意味を持つ数字ではない。４要素に拡張したベクトルに対して、平行移動行列を掛け合わせると、新たなベクトルを得ることができる。

    
       

        

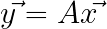
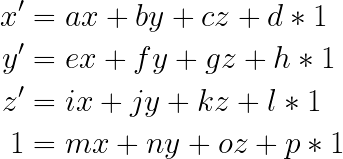
拡大縮小行列（Scale Matrix）

3Dオブジェクトを指定した倍率だけに拡大・縮小させる為の行列。

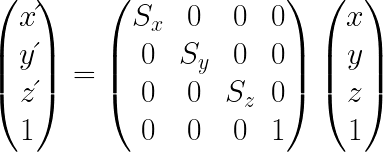
単位行列

WebGLで行列を扱う際に、行列を表現する変数の初期化によく使用される。数字の「１」のように掛け合わせても変化しない行列。

内積（Dot Product）

ベクトルの演算の一つであり、２つのベクトル間の関係性を求めるための数値を計算する操作のこと。

ベクトルA(a1, a2, a3)とベクトルB(b1, b2, b3)の内積をA・Bと表現する。内積は次のように計算される。

A・B = a1 * b1 + a2 * b2 + a3 * b3

内積の結果はスカラー値であり、２つのベクトルがどれだけ同じ方向を向いているか、または直交しているかを示す。直交するベクトルの内積は０になる。

GLSL ES（OpenGL ES Shading Language）

シェーダのプログラミングで使用される言語をシェーダ記述言語という。JavaScriptのコード内で記述する場合は文字列として扱う。

GLSL ・・・OpenGL Shading Language
GLSL ES ・・・OpenGL ES Shading Language

GLSL ESは、主に組み込みシステムやモバイルデバイス、およびGPU（ Graphics Processing Unit ）などの、組み込みGPU上で動作するために、消費電力を抑えたり、ハードウェアに必要な性能をあえて制限して設計されている。

GLSL ESの構文はC言語がベースとなっている。インタプリタ型言語（正確にはJITコンパイラ型）であるJavaScriptと違い、GSLS ESは実行前のコンパイルが必要。

main()から実行される。

GLSL ES は GPU 上で動作する

コメント

//を使用すると、行末までがコメント扱いになる。
/* */で囲うと、囲んだ範囲がコメント扱いになる。

GLSL ES

// 単一行のコメントを書くことができる。

/*
複数行のコメントを書くことができる。
複数行のコメントを書くことができる。
複数行のコメントを書くことができる。
*/

識別子（変数）

先頭に数字は使用することができない。

gl_、webgl_、_webgl_でから始まる変数は使用できない。

データ型

GLSL ESで扱うことができるデータは「数値」と「論理値」の２種類のみ。

また、数値型にはベクトル型のvec2、vec3、行列型のmat2、mat3などの数値をまとまった単位で扱えるものがある。

型	説明
bool	論理値
int	整数
float	浮動小数点数 vec1と同じ意味（vec1という型は実際にはない）
vec2、vec3、vec4	複数個のfloat型の値で構成される型 vecはvector（ベクトル）のこと
ivec2、ivec3、ivec4	複数個のint型の値で構成される型
bvec2、bvec3、bvec4	複数個のbool型の値で構成される型
mat2、mat3、mat4	float型の行列（mat2は2×2、mat3は3×3）で構成される型

ベクトル型と行列型は、コンストラクタによって値を生成する。

GLSL ES

vec2 myVector2 = vec2(1.0, 2.0);
vec3 myVector3 = vec3(1.0, 2.0, 3.0);
vec4 myVector4 = vec4(1.0, 2.0, 3.0, 4.0);

それぞれの要素へは以下のようにアクセスすることができる、

GLSL ES

vec4 myVector4 = vec4(1.0, 2.0, 3.0, 4.0);
float myVector1 = myVector4.x;
vec2 myVector2 = myVector4.xy;
vec3 myVector3 = myVector4.zyx; // 順番を入れ替えてもOK
vec3 myVector3 = myVector4.xxx; // これもOK

アクセス演算子にはバリエーションがある。
.x, .y, .z, .w： ベクトルの要素に直接アクセスすることができる。
.r, .g, .b, .a： 色情報（RGBやアルファチャンネル（透過度））を表現するために使用される。色を扱う際に便利。
.s, .t, .p, .q： テクスチャ座標を表現するために使用される。テクスチャマッピングやUV座標を扱う場合に便利。

どの方法でもアクセスできる値は同じなので、読みやすさのために、用途に合わせて使い分ける。

このような書き方もできる（GLSL ESのバージョンによっては使えないかも）。

GLSL ES

vec3 myVector3 = vec3(1.0, 2.0, 3.0);
vec2 myVector2 = vec2(myVector3.xy); // (1.0, 2.0) となり、3.0は使われない
vec4 myVector4 = vec4(1.0); // （1.0, 1.0, 1.0, 1.0）
vec4 myVector4_2 = vec4(myVector2.xy, myVector2.xy); // この場合はエラーが発生する
vec4 myVector4_3 = vec4(1.0, 2.0); // この場合はエラーが発生する

行列は列優先の行列（Column-Major Matrix）であることに注意する。

上の行列は、GLSL ESではこのようになる。

GLSL ES

mat3 myMatrix3 = mat3(1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0);

要素へのアクセス方法には、JavaScriptのように[]にインデックスを指定する方法もある。

GLSL ES

vec4 myVector4 = vec4(1.0, 2.0, 3.0, 4.0);
float myVector1 = myVector4[0];

インデックスを使用する方法は、特に行列型の各要素にアクセスする際に利用する。列番号と行番号を指定する。

GLSL ES

mat3 myMatrix = mat3(1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0);
float val1 = myMatrix[0][0]; // 1.0  1行目1列目
float val4 = myMatrix[0][1]; // 4.0  1行目2列目

型変換

データ型の型変換には関数を使用する。

関数	説明
int(float)	引数に与えたfloat型int型に変換。小数点以下は切り捨て。
int(bool)	引数に与えたbool型をint型に変換。trueは1、falseは0。
float(int)	引数に与えたint型をfloat型に変換。
float(bool)	引数に与えたfloat型をbool型に変換.trueは1.0、falseは0.0。
bool(int)	引数に与えたint型をbool型に変換。0はfalse、それ以外はtrue。
bool(float)	引数に与えたfloat型をbool型に変換。0.0はfalse、それ以外はtrue。

構造体

GLSL ESでは、構造体（Struct）を使用して、複数のデータをひとまとめにすることができる。構造体は異なるデータだ他の変数をまとめて新しいデータ型を定義する際に使用される。C言語やC++でよく使用される構造体と似た概念。

GLSL ES

struct MyStruct {
  // メンバーの宣言
  float x;
  float y;
  int z;
  vec4 color;
  vec3 position;
};

サンプラ（Sampler）

テクスチャをシェーダ内で扱うための特殊なデータ型。

テクスチャをサンプリングしてピクセルの色や値を取得するために利用される。

GLSL ES

sampler2D mySampler; // 2次元テクスチャサンプラ

型修飾子

型修飾子は変数の振る舞いや、メモリの扱い方を制御するために使用される。

const

定数を宣言するための型修飾子。constによって宣言された変数は、再代入する事ができず、必ず宣言時に初期化を行う必要がある。

GLSL ES

const float PI = 3.14159;

in

関数の引数に使用される。inで受け取った引数は、関数内で変更する事ができない。

GLSL ES

void myFunction(in float x) {
    // xの値を変更できない
}

out

関数の引数に使用される。outで受け取った引数に対関数内の処理は、外部（関数の呼び出し側）にも反映される。

GLSL ES

void myFunction(out float result) {
    result = 1.0;
}

float myValue;
myFunction(myValue); // myValueの値は1.0になる

uniform

頂点シェーダ、フラグメントシェーダの両方で使用する事ができる、グローバル変数として宣言され、使用される（シェーダについては後述）。

uniform変数は、JavaScriptからシェーダ（主に頂点シェーダ）へ値を渡すために使用される。正確には、各頂点、各フラグメントで同一の値を受け取りたい時に使用する。

シェーダ側から見ると、外部から値を受け取るための変数であるため、シェーダ内でuniform変数への再代入はできず、読み取り専用の変数となる。つまり、uniformで宣言した変数は、シェーダの実行ごとに変化しない事が保証されている。

一方で、JavaScript側から見ると、uniform変数はシェーダに値を渡すためのインターフェースとして機能する。光の情報やカメラの位置、テクスチャなどの情報をシェーダに渡すために広く使用される。

頂点シェーダとフラグメントシェーダで同じ名前のuniform変数を宣言すると、両方のシェーダで同じ変数を参照できる。ただし、同じ型、同じ精度修飾子を使用する必要がある点には注意が必要。

配列型、構造体型以外のデータ型に対して使用できる。

また、uniformを使って宣言できる変数の個数には上限があり、ハードウェア（GPU）の性能によって異なる。上限は組み込み定数のgl_MaxVertexAttribsに格納されており、頂点シェーダでは128個、フラグメントシェーダでは16個のuniform変数が宣言できる事が保証されている。正し、これは最低限のサポートであり、特定のハードウェアやバージョンによってはさらに多くのuniform変数を使用できる場合もある。

頂点シェーダ

uniform float uColor;

フラグメントシェーダ

uniform float uColor;

attribute

頂点シェーダで使用される。頂点ごとのデータ（色、座標など）をJavaScriptから頂点シェーダに渡す際に使用される。グローバル変数として宣言して使用する。

頂点シェーダ

attribute vec2 aColor;

float、vec2、vec3、vec4、mat2、mat3、mat4型にしか使用できない。

uniform変数同様に、宣言する事ができる個数は組み込み定数のgl_MaxVertexAttribsで知る事ができる。最小値は8。

WebGL 2.0（GLSL ES 3.0）以降では、attribute変数の代わりにvertex attributeを使用することが推奨されている

uniformとattributeの違い

uniform変数は、各頂点、各フラグメントで同一の値を受け取りたいときに使う。

attribute変数は、バッファオブジェクトとともに使用され、各頂点で異なるデータを受け取りたい時に使う。頂点が受け取るattribute変数に格納されているのは同じバッファオブジェクトだが、バッファオブジェクトに格納した配列データを、各頂点が指定した要素数ずつ取り出して使用するため、結果として各頂点には異なる値が渡る。

varying

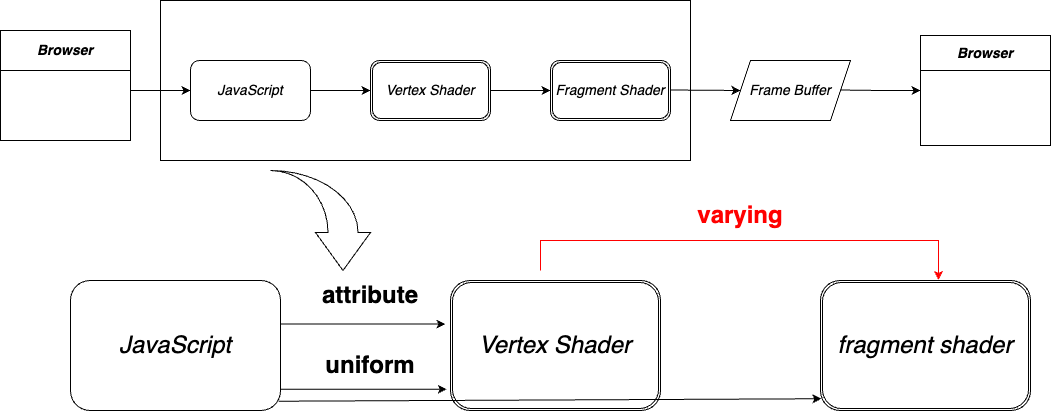
頂点シェーダで計算された値を、フラグメントシェーダに渡す際に使用される。

頂点シェーダ

varying vec4 vColor;

フラグメントシェーダ

varying vec4 vColor; // 頂点シェーダと同じ変数名とする

varyingを使って渡した値は、実際には線形補完されて渡される。

頂点シェーダは各頂点において、それぞれ実行されるため、各頂点がそれぞれvarying変数を保持している。一方で、フラグメントシェーダもフラグメントの数だけ実行される。三角形を例すると、３つの頂点で計算された値は、三角形の内部の複数のフラグメントに渡されることになる。そのとき、各フラグメントの頂点からの距離に応じて、３つの値は補完されてフラグメントシェーダに渡され、滑らかな描画が行われる。

attibute同様に、float、vec2、vec3、vec4、mat2、mat3、mat4型にしか使用できない。

uniform、attribute変数と同様に、宣言できる個数は組み込み定数のgl_MaxVertexAttribsで知る事ができる。最小値は8。

WebGL 2.0（GLSL ES 3.0）以降では、inとout修飾子の組み合わせを使うことが推奨されている

再代入に関して

再代入できる	再代入できない
varying、out、一般的な変数	const、in、uniform、attribute

精度修飾子

変数に格納するデータ（主に浮動小数点数）の精度を指定するための修飾子。

精度を上げるほど必要なメモリ量、計算量、消費電力が増え、パフォーマンスに影響を与える。単純に精度が高い方が良いと言うわけではない。

highp

最も精度の高い（high precision）浮動小数点数。GPUの性能が許す限り高い精度の演算が行われる。

GLSL ES

highp float highPrecisionValue;

midiump

中程度の精度（medium precision）の浮動小数点数。一般的に使用される精度。

GLSL ES

mediump float mediumPrecisionValue;

lowp

最も低い精度の浮動小数点数。速度重視の演算が行われるが、精度が低いために視覚的な品質の低下につながる恐れがある。

GLSL ES

lowp float lowPrecisionValue;

precisionキーワード

精度修飾子の前にprecisionキーワードをつけると、シェーダ全体に対して、精度修飾子を一律で適用させる事ができる。これにより、個別の変数に対していちいち精度を指定する必要がない。

GLSL ES

precision mediump float; // 以降宣言したfloat型はmediumpが適用される

それぞれの型にはデフォルトの精度修飾子が存在する。

型	頂点シェーダにおける精度 / フラグメントシェーダにおける精度
int	highp / mediump
float	highp / なし
sampler2D	lowp / lowp
samplerCube	lowp / lowp

プリプロセッサ指示子（Preprocessor Directive）

プログラムのコンパイル前にソースコードに対して特定の処理を行うための命令。

GLSL ESはコンパイル型の言語。コンパイル型のプログラミング言語は、プログラム実行前に一括でソースコードから機械語への変換が行われる。変換された機械語はGPUで実行される。

プリプロセッサ指示子は、コンパイル前のソースコードを条件付きで有効化したり、無効化できる一方で、コンパイル前に実行されるため、通常はコンパイル時に発覚する構文エラー、スペルミスなどが起きないことに注意する。

プリプロセッサ指示は#とマクロを使用して記述する。

マクロとは、プログラミングにおいて特定のコード片を短いキーワードや記号に置き換える機能のこと。

あらかじめ予約されているマクロには、GL_ESやGL_FRAGMENT_PRECISION_HIGHがある。GL_ESは、OpenGL ESではOpenGL ESがサポートされていることを表す。GL_FRAGMENT_PRECISION_HIGHは、フラグメントシェーダでhighpがサポートされていることを表す。フラグメントシェーダにおけるhighpはデバイスやGPUによってはサポートされていない場合がある。

マクロを定義すると、指定したマクロ名を特定の値や式に置き換える事ができる。

これを利用してプログラム内で何度も使用する値を定数として定義することもできる。定義した定数はシェーダープログラム内で利用できる。

GLSL ES

// マクロの定義
#define PI 3.14159265359

定義したマクロは、未定義にすることもできる。

GLSL ES

// マクロを未定義にする
#undef PI

条件付きコンパイルを行うには、if、ifdef、ifndefを使用する。

GLSL ES

// 条件付きコンパイル

#if 2 * 3 == 6
 // 式がtrueを返す場合に実行される
#else
 // 式がfalseを返す場合に実行される
#endif

#ifdef PI
 // 指定したマクロ名が定義されている場合に実行される
#else
 // 指定したマクロ名が定義されていない場合に実行される
#endif

#ifndef PI
 // 指定したマクロ名が定義されていない場合に実行される
#else
 // 指定したマクロ名が定義されている場合に実行される
#endif

最適化オプションを設定する場合に、#pragmaを使用する事がある。

GLSL ES

#pragma optimize(off)

GLSL ES

関数

GLSL ESで使用する組み込み関数の関数名は、OpenGL ESと同じものが使用されており、「 メソッド名 + 引数の型の頭文字 + 引数の数 」 とな っている。fはfloat、iはint。

また、末尾に「v」がつく場合はベクトル（Vector）を扱う関数であることを意味する。通常、関数名に「v」がつく場合は、関数が各要素に同じ操作をすることを意味する。

GLSL ESの関数は、再起的に呼び出すことはできない。

discard

フラグメントシェーダ内で使用されるキーワード。条件を満たす場合に現在のフラグメントの描画を破棄するために使用される。

フラグメントシェーダ

if (someCondition) {
    discard; // 描画処理を中止して、次のフラグメントの描画処理へ進む
}

シェーダ（Shader）

3Dグラフィックスを処理するためのプログラムの一部であり、WebGLの構成要素の一つ。

頂点シェーダ（Vertex Shader）と、フラグメントシェーダ（Fragment Shader）があり、オブジェクトの外観や光の反射などの特性を制御する役割を持つ。

頂点シェーダとフラグメントシェーダは、それぞれで定義されたmain()から実行される。

WebGLではこの２つを扱うが、OpenGLにはその他のシェーダも存在する。

シェーダは以下の順番で処理される。

シェーダに対する値の渡し方

JavaScriptからシェーダに対して値を渡すときは、attribute変数、もしくはuniform変数を利用する。

attribute変数は、頂点ごとに異なる値を渡す際に使用し、uniform変数は各頂点で共通の値を渡す際に使用する。

uniform変数は頂点シェーダ、フラグメントシェーダに対して使用できる。

一方で、attribute変数は頂点シェーダに対してのみ使用することができる。

頂点シェーダからフラグメントシェーダに対して、頂点ごとに補完された値を渡すにはvarying変数を使用する。

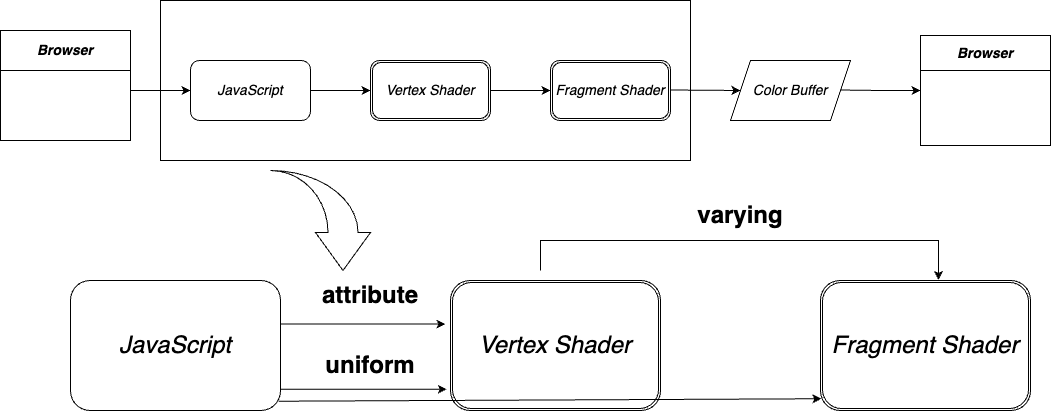
頂点シェーダ（Vertex Shader）

頂点の位置計算を行うためのプログラム。

頂点シェーダでは、頂点の座標を指定するためのgl_Position（vec4型）、サイズを指定するためのgl_PointSize（float型）という組み込み変数によって、3Dオブジェクトの形状、位置などを制御する。

gl_Positionへの値の代入は必須。

頂点シェーダは各頂点ごとに実行される。

バッファオブジェクト

WebGLが提供する、GPU上のメモリ領域に値を格納するためのオブジェクト。

頂点バッファオブジェクト（Vertex Buffer Object, VBO）やインデックスバッファオブジェクト（Index Buffer Object, IBO）など、様々なタイプがある。

OpenGLでは、バッファオブジェクトの他に、頂点配列、頂点配列オブジェクトというものもある。

バッファオブジェクトの使用方法

1. バッファオブジェクトの作成
2. バッファオブジェクトのバインド
3. 値をバッファオブジェクトへ格納する
4. attribute変数への割り当て
5. attribute変数への割り当てを有効化

JavaScript

const buffer = gl.createBuffer(); // バッファオブジェクトの作成
gl.bindBuffer(gl.ARRAY_BUFFER, buffer); // バッファオブジェクトのバインド
const data = new Float32Array([0.0, 0.0, 1.0, 1.0, 1.0, 0.0]); // 格納する値
gl.bufferData(gl.ARRAY_BUFFER, data, gl.STATIC_DRAW); // バッファオブジェクトへ格納する
// 頂点シェーダープログラム内での頂点属性（attribute）の定義
const vertexShaderCode = `
    attribute vec2 position;
    void main() {
        gl_Position = vec4(position, 0.0, 1.0);
    }
`;

...
const positionLocation = gl.getAttribLocation(program, "position"); // position属性の位置を取得
gl.vertexAttribPointer(positionLocation, 2, gl.FLOAT, false, 0, 0); // attribute変数への割り当て
gl.bindBuffer(gl.ARRAY_BUFFER, null); // attibute変数に割り当て後は、バインドは必要ないため、解除する
gl.enableVertexAttribArray(positionLocation); // attribute変数への割り当てを有効化

1. バッファオブジェクトの作成

WebGLRenderingContext.createBuffer()を使用して、バッファオブジェクトを生成する。

const buffer = gl.createBuffer(); // バッファオブジェクトの作成

2. バッファオブジェクトのバインド

WebGLRenderingContext.bindBuffer()を使用して、バッファオブジェクトをシェーダープログラムに関連付ける（バインドする）。

void gl.bindBuffer(target, buffer);
指定したターゲットに対して、特定のバッファオブジェクトを関連付け（バインド）する。

target：バインド対象
        gl.ARRAY_BUFFER（頂点属性データを格納するバッファ）
        gl.ELEMENT_ARRAY_BUFFER（インデックスデータを格納するバッファ）
        WebGL2では他にも、gl.COPY_READ_BUFFER、gl.TRANSFORM_FEEDBACK_BUFFER、gl.UNIFORM_BUFFER、gl.PIXEL_PACK_BUFFER、gl.PIXEL_UNPACK_BUFFERなどがある
buffer：バインドするバッファオブジェクト

gl.bindBuffer(gl.ARRAY_BUFFER, buffer); // バッファオブジェクトのバインド

3. 値の格納

WebGLRenderingContext.bufferData()を使用して、データをバッファオブジェクトに格納する。

WebGL2
void gl.bufferData(target, ArrayBufferView srcData, usage, srcOffset, length)；
頂点データやインデックスデータをGPUに転送し、指定したバッファオブジェクトにデータを格納する。

srcData：バッファオブジェクトへ格納する、型付き配列型のデータ
usage：格納した値の用途。バッファオブジェクトのメモリ上の格納先に影響を与える。正しく指定することで処理が早くなる。
        gl.STATIC_DRAW（データが変更されない。頻繁に使用される。）
        gl.STREAM_DRAW（データがあまり変更されない。数回しか使用されない。）
        gl.DYNAMIC_DRAW（データが繰り返し変更される。頻繁に使用される。）
srcOffset：srcDataの一部を格納する場合に、対象範囲を指定する際に使用する。開始位置のオフセットを指定する（省略可）（オフセットは基準位置からの距離）
length：srcDataの一部を格納する場合に、対象範囲を指定する際に使用する。要素数を指定する。

4. バッファオブジェクトのattribute変数への割り当て

WebGLRenderingContext.vertexAttribPointer()を使用して、データを格納したバッファオブジェクトを、atribute変数に対して割り当てる。このメソッドのみでは割り当ては有効化されない。

gl.vertexAttribPointer(location, size, type, notmalized, stride, offset)

location：attribute変数の格納場所
size：1頂点あたりの成分数。1~4。例えば、2を指定した場合、配列に格納した値は2つずつのセットで扱われる。
type：データの形式。
        gl.UNSIGNED_BYTE（符号なしバイト。Unit8Arrayに対応。）
        gl.SHORT（符号つき単精度整数。init16Arrayに対応。）
        gl.UNSIGNED_SHORT（符号なし単精度整数。Unit16Arrayに対応。）
        gl.INT（符号つき整数。Int32Arrayに対応。）
        gl.UNSIGNED_INT（符号なし整数。Unit32Arrayに対応。）
        gl.FLOAT（浮動小数点数。Float32Arrayに対応。）
normalized：値を整数で指定する場合に、[0, 1]もしくは[-1, 1]の範囲に正規化するかどうか
stride：頂点データの値同士の間隔
offset：バッファオブジェクト内における、対象データのオフセット（オフセットは基準位置からの距離。この場合の基準位置はバッファオブジェクトの先頭。）

5. attribute変数へのバッファオブジェクト割り当てを有効化

WebGLRenderingContext.enableVertexAttribArray()を使用して、バッファオブジェクトのattribute変数への割り当てを有効化する。有効化した後は、値の格納ができなくなる。無効化するにはWebGLRenderingContext.disableVertexAttribArray()を使用する。また、有効化しなかった場合、固定のデフォルト値が使用される。

フラグメントシェーダ（Fragment Shader）

フラグメント（ピクセル）ごとに色や特性を計算し、3Dオブジェクトの表面の色や光の反射を制御するためのプログラム。

WebGLではピクセルをフラグメントと表現するため、他の分野ではピクセルシェーダと呼ばれていることもある。

フラグメントシェーダには、フラグメントの色をRGBAで指定するgl_FragColor（vec4型）という変数がある。

フラグメントシェーダは、フラグメントごとに実行される。各フラグメントはラスタライズ処理によって生成される。

フラグメントシェーダは、各フラグメントごとに実行される。

ラスタライズ（Rasterize）

描画の際に行われる３Dオブジェクトを２D画像として表示するためのピクセルに変換するプロセスのこと。３Dグラフィックスパイプラインの一部。ピクセルとは、画素とも呼ばれる、デジタル画面を構成する最小単位の点のこと。

一般的には、ラスタライズは、ベクタ形式の画像をラスタ形式に変換することを指す場合が多い。

フラグメントシェーダで、ポリゴンの各頂点に異なる色を指定した場合、ラスタライズでは色の補完処理が行われる。

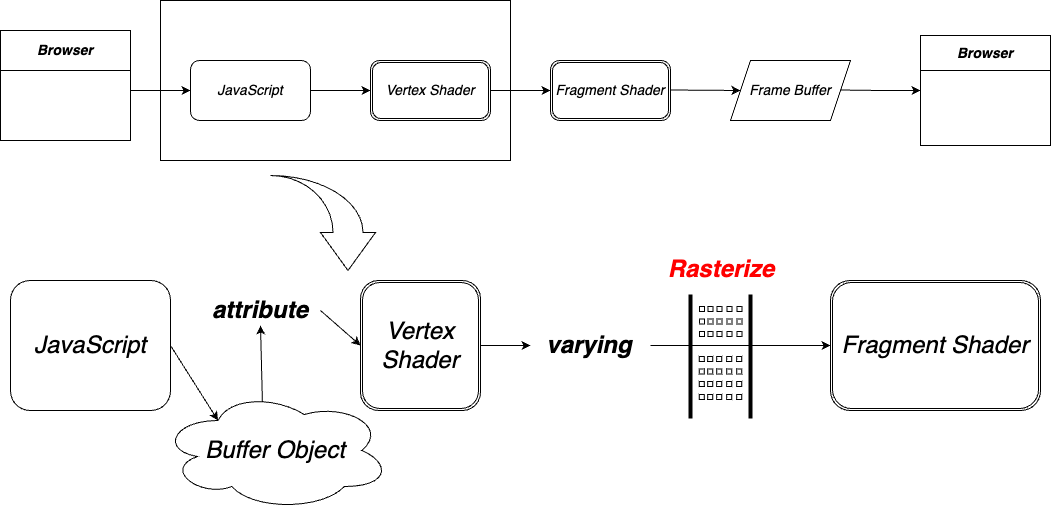
描画に関わる知識、用語の整理

WebGLでは、すべてのオブジェクトは基本的に以下の３種類によって構成されている。

• 点（Points）
• 線（Lines）
• 三角形（Triangles）

WebGLでは点、線、三角形の組み合わせで物体（オブジェクト）を描画する

三角形の数を膨大にすれば、細かくリアルな描画にすることができるが、数を増やすだけ計算量が増えるため、単に細かく描画すれば良いというものでもなく、バランスも考慮しなけらばならない。

void gl.drawArrays(mode, first, count);
配列データからプリミティブの種類を指定し、描画を行う。プリミティブは、ポイント、線、三角形といった基本的な形状を指す。
mode：プリミティブの種類
        gl.POINTS（単一の点）
        gl.LINES（２つの頂点に対する線）
        gl.LINE_STRIP（次の線に続く直線）
        gl.LINE_LOOP（次の線に続く直線。最初と最後の頂点は接続される。）
        gl.TRIANGLES（３つの頂点に対する三角形）
        gl.TRIANGLE_STRIP（連続する三角形）
        gl.TRIANGLE_FAN（中心点を中心にした放射状の三角形）
first：頂点ベクトルの配列の開始インデックス
count：描画するインデック流の数

プリミティブ

WebGLRenderingContext.drawArrays()で指定できるプリミティブタイプの実際の形は以下の通り。点、線、三角形の組み合わせであることがわかる。

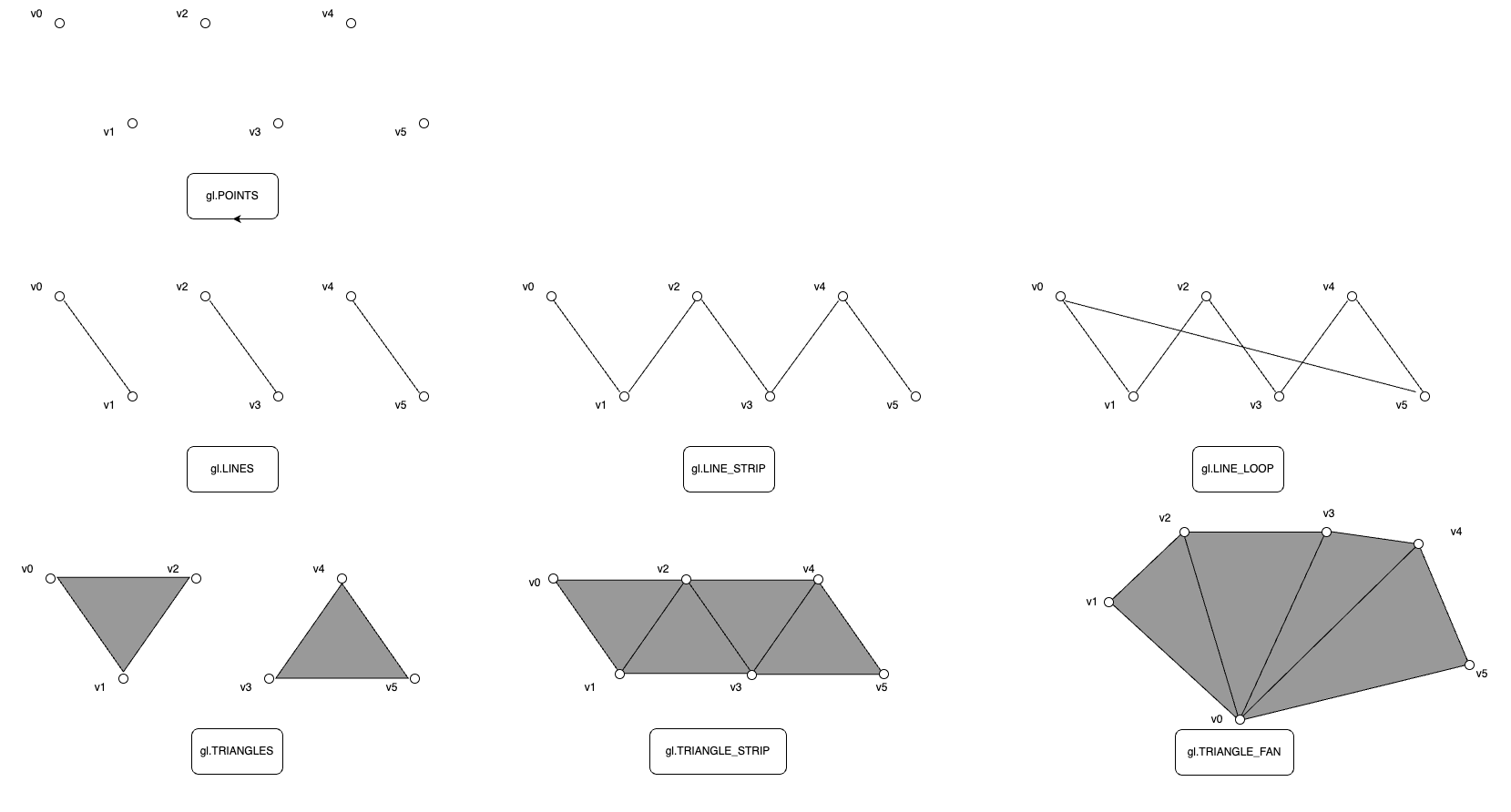
シーン（Scene）

3Dグラフィックスにおいて、オブジェクトやライト、カメラなどの要素が配置された環境や空間のこと。

シーンには、3Dモデルやテクスチャ、光源の設定、カメラの位置や視野範囲などが含まれることが一般的。これらの要素を組み合わせてシーンを構築し、描画やアニメーションの処理を行う。

ポリゴン（Polygon）

ポリゴン（Polygon）とは３Dオブジェクトを構成する平面図形のこと。最も一般的なポリゴンは三角形だが、ポリゴンには四角形や五角形も含まれる。３Dモデルの基本的な構成要素のひとつであり、テクスチャや法線などの属性情報を持つことができる。

通常、ポリゴンは３つ以上の頂点を持ち、それらの頂点を結ぶことによって閉じた図形を形成する。ポリゴンの頂点を結ぶ順番には、CW（Clockwise）は時計回り、CCW（Counter Clockwise）は反時計回りがあり、カリングや法線ベクトルの計算に影響を与える。

法線（Normal）

法線（Normal）とは、３次元空間において平面や曲面上の点が属する平面に対して垂直な方向を示すベクトルのこと。球体などが持つ曲面も、それぞれの点に対して局面があり、法線はその局面上の点に垂直な方向を示すため、局面に対して垂直になっている。

法線ベクトルは単位ベクトルとしての役割を持つ。つまり、大きさとしての情報を持たない。

実際に扱う際には、法線はが一つの面に対して正方向と負方向の２つがある。また、どの座標においても、法線はその座標が属する原点を含む面の原点からのベクトルで表現する。つまり、同じ面に属する座標の法線は全て同じ。

法線は、ポリゴンの各頂点に関連付けられる。ポリゴンの各頂点における法線は、周囲の面の法線の平均値として計算される事が多い。これにより、頂点が共有される複数のポリゴンがある場合に、滑らかに陰影をつける事ができる。

法線は、３Dオブジェクトへの光の当たり方やシェーディングの計算に使用される。法線の方向によって光が物体の表面に当たる角度や明るさが変化し、リアルな３D表現が可能となる。

法線は、オブジェクトが移動、回転、拡大・縮小されると変わる事があり、これを逆転置行列という行列を用いて補正する事がある。

フレームバッファ（Frame Buffer）

コンピュータグラフィックスにおいて、描画結果を格納するためのメモリ領域のこと。主に、カラーバッファ、デプスバッファ、ステンシルバッファなどで構成される。

• カラーバッファ
• デプスバッファ
• ステンシルバッファ

カラーバッファ（Color Buffer）

オブジェクトの色情報が格納されるバッファ。

OpenGL において、3DCGの描画結果を格納するメモリ領域をカラーバッファと呼び、この用語は WebGL においては、カラーバッファに描画した内容がcanvas要素に描画されるようになっている。

カラーバッファは、画面に表示されるフロントバッファと、表示されないバックバッファの２つから構成される。描画処理を繰り返す際に、まずバックバッファに対して描画を行い、その後でフロントバッファとバックバッファを入れ替えることで画面のチラつきを防ぐ事ができる。この入れ替え処理をバブルバッファリングと呼ぶ。WebGLではブラウザがこの入れ替え処理を<canvas>要素内で自動的に行なっている。

また、カラーバッファをクリアするとは、特定の領域を指定した色で塗りつぶすことを意味する。これにより、前回のフレームの描画内容を消去して、新しい描画を開始する事ができる。

カラーバッファを「clearする」とは特定の領域を「塗りつぶす」ことを意味する。

デプスバッファ（Depth Buffer）

オブジェクトの奥行き（Z座標）情報を格納するためのバッファ。

３Dグラフィックスでは、オブジェクトがカメラから見てどのように配置されているかによって奥行きが異なる。奥にあるオブジェクトは手前にあるオブジェクトよりも先に描画される必要がある。デプスバッファは各フラグメントの奥行き値を保持しており、オブジェクトがカメラから見て重なっている場合、デプスバッファの値を比較することにより、手前のオブジェクトのみが描画される。WebGLではこれを隠面消去（Hidden Surface Removal）という。このように、奥行き情報を正確に管理することで、オブジェクトの重なりや遮蔽関係を適切に表現する事ができる。

デプスバッファは通常、カラーバッファと同じ解像度で設定され、対応するフラグメントごとに奥行き情報を保持する。また、値は０から１までの範囲に正規化されている。

ステンシルバッファ（Stencil Buffer）

オブジェクトの描画領域を制御するためのバッファ。主にステンシルテスト（Stencil Test）と呼ばれる描画テクニックで使用される。Stencilには型紙、原紙といった意味がある。

ステンシルバッファは、カラーバッファやデプスバッファと同様に、各フラグメントごとに対応している。各フラグメントには、ステンシル値という整数値が関連づけられている（浮動小数点数ではない）。

ステンシルテストとは、ステンシルバッファの値と特定のテスト条件を用いて、特定のフラグメントがオブジェクトの描画範囲内にあるかどうか（描画すべきフラグメントであるかどうか）を判断するテクニックのこと。ステンシルバッファの値を書き換えることで、描画範囲を制御する事ができる。

ステンシルテストは、主に次のような場面で使用される。

• クリッピング：特定の領域以外を描画しないようにする
• マスキング：特定の領域をマスクして、他のオブジェクトに影響を与えないようにする
• 彫り抜き効果：オブジェクトが他のオブジェクトによって遮られた場合に、遮られた部分を透明にするなどの効果を実現する

必ず使用するものではなく、高度なテクニックとして位置付けられる。

Z-ファイティング（Z-fighting）

主にデプスバッファを使用する際に発生する問題。

デプスバッファに格納できる情報の精度には限界があり、特に近接しているオブジェクト同士では、正しく前後関係が判断されない場合があり、これをZ-ファイティングという。

Z座標が被らないように気を付けることで回避できるが、アニメーション時などはそれが難しい場合もある。その場合、ポリゴンオフセット機能を使用する。

ポリゴンオフセット機能

Z-ファイティングを軽減するための手法の一つ。

描画するポリゴンの奥行き値に微小なオフセットを加えることで、オブジェクトの奥行きが微妙にシフトし、Z-ファイティングを回避する事ができる。

視体積（View Volumn）

３Dグラフィックスにおいて、カメラ（視点）から見たシーンの表示範囲を定義する仮想の空間のこと。視体積はカメラの位置と向きによって決まり、その範囲内に含まれるオブジェクトのみが描画される。視野の範囲は３次元空間上では立体になるため、「体積」と呼ばれる。

視体積を指定する方法には直方体で指定する方法（平行投影）と四角錐で指定する方法（透視投影）がある。直方体型の視体積を設定する行列を平行投影行列と言い、四角錐型の視体積を設定する行列を透視投影行列と言う。

視体積は通常、６つの面に囲まれた立方体として定義される。これらの平面はクリッピング平面と呼ばれ、シーンに含まれるオブジェクトが描画範囲内に収まるように制限する役割を果たす。

カリング（Culling）

３Dグラフィックスにおいて、カメラから不可視であるオブジェクトの裏側を描画しないことによって、GPUにかかる負荷を軽減し、効率よく描画する技術。パフォーマンスに影響を与える技術であり、カリングの設定有無が描画内容に影響を与えることはない。

裏側を描画しない手法をバックフェースカリング（Backface Culling）と言い、表側を描画しない手法をフロントフェースカリング（Frontface Culling）という。

３Dオブジェクトは通常、ポリゴンの集合体で構成されている。これらのポリゴンには、画面に向かって見える側（フロントフェース）と、画面から離れて見えない側（バックフェース）がある。

バックフェースカリングが適用されると、フロントフェースに存在するポリゴンのみが描画されるようになる。

バックフェースカリングを行うためには、ポリゴンの表と裏を区別する必要があり、この判断にはポリゴンの各頂点における法線ベクトルが利用される。

具体的には、３Dオブジェクトの各面の法線ベクトルと、カメラの方向ベクトルとの内積を計算することで表裏の判断が行われる。内積が正の値なら表側を向いており、負の値なら裏側を向いていることを意味する。裏側を向いている面に対しては、カリングが行われる。

同次座標系（Homogeneous Coordinates）

3次元空間における座標系を拡張する手法の一つ。３次元空間では通常３つの要素（X, Y, Z）を持つ座標が使用されるが、同次座標系では４つの要素（X, Y, Z, W）を持つ座標を使用し、拡張された４つ目の要素Wには通常１が設定される。

回転行列や、平行移動行列に利用することで、３次元空間における計算がより効率的に行えるようになる（前述）。

ローカル座標（Local Coordinates）

オブジェクト自体が持つ座標系。オブジェクト座標とも呼ばれる。

オブジェクトの中心や軸に対して相対的な座標を表現する。たとえば立方体のローカル座標では、立方体の中心を原点として、各面や辺に対して想定的な座標を持つ。

ゲームのキャラクタのようなオブジェクトであれば、足下を原点にすることで、Y座標が0の時に地面の上に立っているように見せる事が多い。Y座標を変えずにZ座標、Z座標を変えると歩いているように見せる事ができる。

ワールド座標（World Coordinates）

ローカル座標をモデル変換（Model Transformation）して得られる座標系。モデル変換は、ワールド変換とも呼ばれる。モデル変換には、座標変換行列が使用される。

ワールド座標は、3D空間全体を表す座標系を指す。シーン内のすべてのオブジェクトが配置される共通の座標系であり、オブジェクトの位置や方向を表現する。

シーン内のすべてのオブジェクトは絶対的な座標を持ち、相対的な位置関係や方向関係を表現することができる。

ローカル座標で作成したゲームのキャラクタが１つの空間内に複数登場する状況では、ワールド座標が同じ場合、同じ位置に立っているように見える。

ワールド座標系は、世界座標系、グローバル座標系とも呼ばれる。

ビュー座標（View Coordinates）

ワールド座標からビュー変換（View Transformation）して得られる座標系。

カメラの視点を基準とした座標系のこと。シーンをカメラの視点から見た相対的な座標を表現する。

クリップ座標（Clip Coordinates）

ビュー座標をプロジェクション変換（Projection Transformation）して得られる座標系。プロジェクション変換は射影変換とも呼ばれる。

オブジェクトの座標系をカメラの前に配置されたクリップ空間（クリップボリューム）にマップするための座標系。このクリップ空間は、通常は正規化デバイス座標系と呼ばれる規格化された空間マップに変換され、さらにその後、スクリーン座標系に変換されて実際の描画が行われる。

クリップ座標は、3Dオブジェクトがカメラの視錐体内に収まるかどうかをチェックするために使用される。視錐体内に収まらない部分はクリップされ、表示されないようにする必要がある。つまり、クリップ空間は有限の空間。

クリップ座標の範囲は、通常、-1から1まで。クリップ座標では、各頂点は通常4次元ベクトル（x, y, z, w）として表され、最終的なクリップ空間座標を得るために透視除算が行われる。

クリップ座標以降は左手の座標系になることに注意する

正規化デバイス座標系（Normalized Device Coordinates）

クリップ座標をクリップ空間の範囲（通常は -1 から 1）に正規化した座標系。プロジェクション変換の過程に含まれる座標系。

視体積内に収まるかどうかの判定やクリッピングに使用される。

スクリーン座標（Screen Coordinates）

正規化デバイス座標をスクリーンのピクセル座標に変換した座標系。

実際のコンピュータ画面上のピクセル座標系で、2D画面上での座標や位置を表現する。スクリーン座標系では、オブジェクトの位置や方向を画面上のピクセル座標で表現する。一般的に、左上隅を原点として、水平方向が右向き、垂直方向が下向きになり（X, Y）のように表現される。

ディスプレイの解像度が1920×1080ピクセルの場合、スクリーン座標系の原点は左上隅になり、右下隅は（1919, 1079）になり、画面全体は(0, 0)から（1919, 1079）の範囲になる。

グラフィックスパイプライン（Graphics Pipeline）

コンピュータグラフィックスの描画プロセスを、論理的なステップに分割して実行する仕組み。モデル変換、ビュー変換、プロジェクション変換が行われる。

WebGLのグラフィックスパイプラインは、主要なステップが次のようになる。

1. 頂点データの入力（Input Assembly）
   バッファオブジェクトと呼ばれるデータバッファに頂点データを格納して、それをGPUに渡す。

2. 頂点シェーダ（Vertex Shader）
   頂点シェーダは頂点データを受け取り、3D空間内での位置を計算したり、色やテクスチャ座標などの情報を変換する。

3. プリミティブの組み立て（Primitive Assembly）
   頂点シェーダの出力を基に、プリミティブ（三角形、点、線など）を組み立てる。

4. ジオメトリシェーダ（Geometry Shader）（一部のパイプラインに存在）
   WebGLはOpenGL ES 3.0以降でのみジオメトリシェーダがサポートされている。ジオメトリシェーダはプリミティブを受け取り、追加の頂点やプリミティブを生成する。

5. ラスタライズ（Rasterization）
   プリミティブの頂点が2D画面上のピクセル座標に変換される。

6. フラグメントシェーダ（Fragment Shader）
   ラスタライズで生成された各ピクセルに対して、ピクセルシェーダが実行される。ピクセルシェーダは、各ピクセルの色、深度、テクスチャ情報などを計算する。

7. 出力マージ（Output Merge）
   ピクセルシェーダの出力が画面上に描画される前に、出力マージステージで最終的なピクセルの色が計算される。

テクスチャ（Texture）

2Dオブジェクトや3Dオブジェクトの質感を表現するための画像データのこと。３Dオブジェクトの表面に貼り付けることで、リアルな質感やディティールを表現するのに使用される。

テクスチャを使用するには、テクスチャ画像が必要。テクスチャ画像はテクセル（Texture Elememt）と呼ばれる小さな部品から構成されている。

テクスチャに画像を使用する際は、、元の画像の各辺が２の累乗である必要がある。例えば256×256、1024×1024など。これはハードウェアの制約やアルゴリズムの最適化によるものであり、２の累乗ではない場合、テクスチャの拡大や縮小時に補完が行われるため、画像がぼやけたり歪んだりする可能性がある。ただし、近年のハードウェアやプラットフォームでは、２の累乗ではないテクスチャもサポートされており、画像の崩れを最小限に抑える機能が実装されている事が多い。

テクスチャ座標

サンプリング

テクスチャに格納されたピクセルデータを取得するプロセスをサンプリングという。データの取得はテクスチャサンプラを使用して行われる。

テクスチャユニット（Texture Unit）

テクスチャユニットとは、複数のテクスチャを処理するための仕組みのこと。

複数のテクスチャが同時に使用される場合に、テクスチャユニットは、各テクスチャに固有の番号（インデックス）を割り当てることで、プログラム内でそれぞれのテクスチャを識別する。ただし、扱う画像が１枚であってもテクスチャユニットを使用する必要がある。

テクスチャユニットは、テクスチャをバインドすることによってアクティブになり、バインドされたテクスチャを使用して描画やシェーダプログラムの処理を行う。

一般的に、グラフィックスプログラムは複数のテクスチャユニットを持ち、それぞれのユニットが異なるテクスチャを扱う。これにより、複数のテクスチャを同時に使用して複雑なビジュアル効果を実現することができる。

シェーディング（Shading）

現実世界では物体への光の当たり方によって、表面には陰影（明暗）がついて見える。これを表現する技術はシェーディングと呼ばれる。

シェーディングによって表現した物体には、リアルな質感や陰影がつき、立体的に見えるようになる。

一般的なシェーディング手法には以下のようなものがある。

• フラットシェーディング
  各ポリゴンを一様な色で表現
• グローシェーディング
  光源に向かって発光しているような色を表現
• フォングシェーディング
  ポリゴンの法線に基づく計算によって、光の反射を表現
• フィジカルベースシェーディング
  物理的な光の振る舞いをシュミレートする高度な手法

シャドウイング（Shadowing）

物体自体に陰影をつける技術をシェーディングというのに対して、床に落ちる物体の影を表現する技術をシャドウイングという。

シャドウイングによって、物体同士の位置関係をよりリアルに表現する事ができる。

• レイキャスティング
  視点から光源までのレイを追跡し、オブジェクトとの交差を検出することで影を表現する。高度な表現が可能である一方で、計算量が多くなる傾向がある。
• シャドウマップ
  光源からの視点を別のカメラとしてシュミレートし、シーンをテクスチャとして保存する手法。テクスチャを使用して影を描画することで、計算量を削減し、リアルタイムに影を表現できる。

平行光源（Directional Light）

太陽光をモデル化したもの。

太陽のように無限に近いくらい遠いところ（無限遠）から一定の方向に向かって、一様な光を発する光源。

全てのポリゴンに対して同じ方向からの光が平行にあたるため、物体の表面には陰影（明暗）がなく、一様な明るさで照らされるように見える。

位置を持たず、光の向きと色情報だけを指定する。

主に、シーン全体を均一に照らすために使用される。

点光源（Point Light）

電球、ランプ、炎をモデル化したもの。

一点から全ての方向に対して球状かつ放射状に光を発する光源。

光源からの距離に応じて明るさが減衰するため、光源から遠いオブジェクトはより暗く、近いオブジェクトはより明るくなる。

全方向に対する光源なので、位置と色のみを指定する。

特定の位置に存在する光源を表現するために使用される。

環境光（Ambient Light）

壁などに当たった光が間接的に他の物体まで届く間接光をモデル化したもの。

シーン全体を均一に照らす微弱な光。平行光源、点光源によって照らされていない部分を照らす役割を持つ。影響範囲は無限遠まで及び、光源の方向は指定されない。

シーン全体に均一な明るさを与えるために使用される。また、主光源（平行光源、点光源など）による陰影を和らげるのにも使用される。

全ての方向から物体に対してあたる光であるため、色のみを指定する。

拡散反射（Diffuse Reflection）

平行光源、点光源からの光に対する反射。乱反射とも呼ばれる。

物体の表面が光を受けた時に、ランダムな方向に、均一に反射する現象。

物体表面の粗さや、テクスチャなどに影響される。物体の表面が粗いほど光が均一に反射される範囲が広くなり、つやのある物体よりもマットな質感になる。

物体表面の法線ベクトルと、光の入射ベクトルとの間の角度によって計算される。maxは引数の内、大きな方の値を返す。cosθは、物体表面の法線ベクトルと光の入射ベクトルの内積（法線ベクトル・光の入射ベクトル）によって求まる。

環境反射（Ambient Reflection）

環境光に対する反射。

光源からの直接的な光ではなく、周囲の環境からの間接的な光の影響を表現する。物体がどの程度、周囲の光によって照らされるかを表す。

物体は周囲の光や環境の色を一部反射し、物体が置かれている環境の明るさや色を反映する。環境反射は、光源から物体が直接光を受けない場合でも、周囲の光の影響により影の部分の明るさが保たれる。物体の陰影を柔らかくしたらい、全体的な光のバランスを調整するために使用される。

環境反射は、以下の要素によって構成される。

• 環境光（Ambient Light）
  光源からの直接の光ではなく、周囲の環境から当たる光。
• 環境反射係数（Ambient Reflectance）
  物体が環境光をどの程度反射するかを表す係数で、物体の表面の色に影響を与える。

シーン全体に、一様な照明を与えたい場合、環境反射係数を定数として設定し、オブジェクトの色に環境反射係数を掛け合わせることで環境反射を表現する。

環境反射によるオブジェクトの色 = オブジェクトの原色 * 環境反射係数

また、環境マップと呼ばれる特殊なテクスチャを使って、よりリアルな環境反射を得ることもできる。環境マップとは、周囲の光環境をテクスチャとして表現したもの。環境マップを使用する場合、オブジェクトの法線ベクトルを使って観葉マップから対応する環境光の色をサンプリングし、それをオブジェクトの色に乗算する。

シーン全体に影響を与えるため、全体の明るさを調整し、物体をより自然な環境に統合させる効果がある。

鏡面反射(Specular Reflection)

物体の表面が鏡のように光を反射する現象を表現するための反射のテクニック。

光源からの光が物体表面で鏡のように反射され、特定の角度において視線方向と反射方向が一致したときに明るく輝く光の現象。鏡面反射により、物体の表面が光の強い光沢を持ち、鏡面光が現れることで光源の位置に応じて明るく光る部分が生じる。

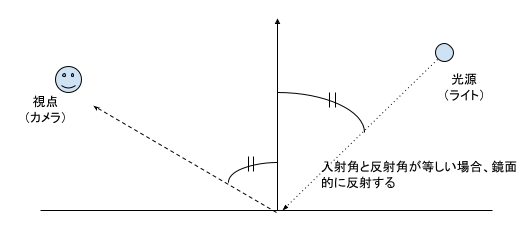
光源からの入射ベクトルと法線ベクトルによって計算される反射ベクトルと、視線ベクトルの間の角度に応じて光の強さが変化する。鏡面反射により、物体の表面が光り輝く効果が得られる。

鏡面反射は以下の要素から構成される。

• 光源の位置と方向
  物体の表面に対して鏡面光が現れる角度を決定する。
• 視線方向
  鏡面光が視線方向と一致したときに強調される。
• 鏡面反射係数（Specular Reflectance）
  物体が鏡面光をどの程度反射するかを表す係数で、物体の表面の色や光沢に影響を与える。

参考

・WebGL+HTML5 3DCGプログラミング入門　松田 晃一 (著)

・The Book of Shaders

・WebGL2の基本

・MDN Web Docs

・wgld.org

・Hack The WebGL

・Not Equal | 差別化できるWeb制作