行列解析を布教したい

この記事は東京大学工学部応用物理学系2学科(物工/計数) Advent Calender2023のために書かれたものです．

はじめに

東京大学物理工学科3年の@Aoi97792739(Twitter)です．

今回は，題名の通り行列解析という分野の布教をします．

これを読んでいるほとんどの方はB1のときに線形代数を学んだかと思います。私も2年前に死ぬ気で過去問を解きまくって単位を取りました．習った範囲は行列の記号，ベクトル空間，線型写像，計量ベクトル空間，行列式，対角化，二次形式でした．大体の人が同じようなものだと思います¹．

これらの基本的な内容にとどまらず，行列にはもっと深いトピックがたくさんあります．本記事では，majorizationとKarpelevič²の定理について紹介します．

行列解析とは

行列解析とは，簡単に言えば有限次元を記述する理論です．もっと砕けて言えば線形代数の行列に関する部分を発展させた感じです．先人による天才的な証明が多く，学んでいてとても楽しい分野です．

和書だと，SGCライブラリの行列解析の基礎(山本)，同じくSGCライブラリの行列解析ノート(山本)が詳しいです．量子情報と行列解析を併せて解説している，これまたSGCライブラリの行列解析から学ぶ量子情報の数理(日合)もよいです．洋書だと，Springer社のMatrix Analysis(R. Bhatia)などが知られています．PDFだと白石直人先生の物理数学の講義ノートがとてもよいです．

majorization

majorizationについて紹介します．

考える古典確率分布を$p$と$p'$とします．このとき，$p=(p_1,p_2,\ldots,p_d)^{\mathsf{T}}$の成分を昇順に並べて$p_1^{\downarrow}\geq p_2^{\downarrow}\geq\cdots p_d^{\downarrow}$と書き直します．$p'$の成分についても同様に${p_i'}^{\downarrow}$を定めます．

このとき，「$p$が$p'$をmajorizeしている」とは，

1\leq\hspace{-3mm}\phantom{a}^{\forall}k\leq d,\ \ 
\sum_{i=1}^k{p_i'}^{\downarrow}\leq\sum_{i=1}^kp_i^{\downarrow}

が成立することであり，これを$p'\prec p$と書きます．この関係は，任意の$p,p'$について$p'\prec p$または$p\prec p'$とはならないので，半順序関係をなします．

$p'\prec p$のとき，$p'$が$p$よりも乱雑ということができます．ここでは載せませんがこの関係はLorenz曲線によって可視化することができます．

ここで，Hardy-Littlewood-Polyaの定理を紹介します．これはmajorizationの必要十分条件を示します．$T$は二重確率行列です．³

p'\prec p\ \Longleftrightarrow\ ^{\exists}T,\ p'=Tp

この定理は，行列解析ノート(山本)の2章でとても美しく示されています．

さて，先ほどの説明で「乱雑」と聞いてエントロピーを思い出した方もいるかもしれません．majorizationは情報理論，熱力学，量子情報，経済学，統計学⁴などさまざまなところで有用な尺度です．

ここでは，熱力学，量子情報を念頭に説明します．よく使われる乱雑さの尺度であるShannonエントロピー，Von Neumannエントロピーには「単調性」という性質がありますが，これだけではエントロピーが大小関係をもつ必要十分条件を議論することはできません．しかし，majorizationの考え方を用いると，先ほど紹介したHardy-Littlewood-Polyaの定理によって乱雑さの必要十分条件を議論することができるため，尺度としてより完全です．

もう少し具体的に説明します．熱力学において，一般化されたmajorizationは，有限温度でGibbs保存写像によって記述される熱力学に，実行可能な変換の必要十分条件を特徴づけるというとても重要な役割を果たすのです．⁵これは量子系にも応用できます．与えられた量子状態からどれだけエンタングルメントを取り出せるかを考えることができます．

Karpelevičの定理

Karpelevičの定理について紹介します．

まず，確率行列の固有値はGerschgorin⁶の定理により，任意の固有値$\lambda$は複素平面上で必ず単位円$|\lambda|\leq1$の中に分布することが知られています．しかし，これはアバウトな絞り込みであり，$|\lambda|\leq1$さえ満たせば必ず確率行列の固有値となるわけではありません．この厳密な境界を示すのがKarpelevičの定理です．境界は，パラメタ表示された方程式の解によって与えられるのですがこの方程式の説明は面倒なので割愛します．気になる人はH. Minc,Nonnegative Matrices,Wiley Series in Discrete Mathematics and Optimization,1988の176ページ以降を参照してください．2016年の論文に確率行列の次元が$n=3,4,5$のときの境界が示されていたので引用しておきます．

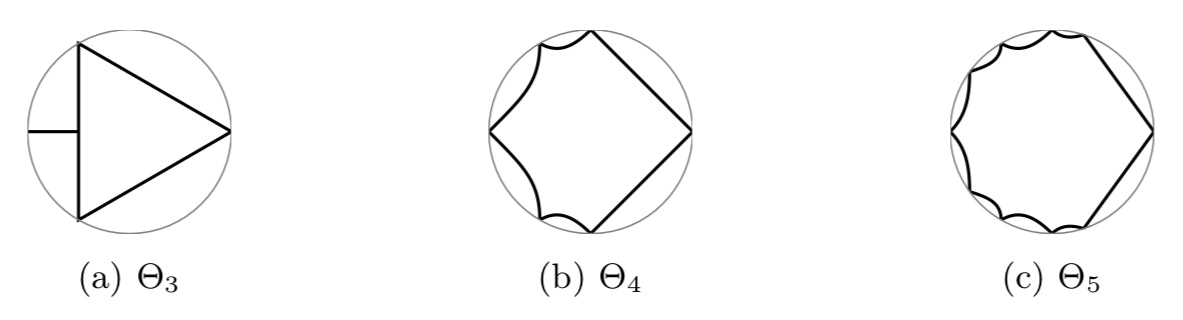
不思議な形をしています．実軸について対称であること，実数はすべて固有値となりうることが分かります．

この定理が和書で示されているところを見たことありません．「カーペレビッチの定理」で検索すると，とある方のブログ記事が2件ヒットするのみです．しかし，Karpelevičで検索するといろんな文献が出てきました．先ほど引用した2016年の論文によると，Karpelevičの定理はステートメントが扱いにくかったようで1997年に伊藤尚史先生によって簡略化されたようです．⁷この先生についていろいろ調べたところ，応物の「基礎数理」を担当されている岩田覚先生との共著論文が見つかりました．計数で博士を取った方のようです．このようなマイナーな定理と応物につながりがあると知って大変驚きました．こんなことあるんですね．

終わりに

いかがだったでしょうか．あまり突っ込んだ説明はできませんでしたが行列解析の奥深さを少しでも感じていただけたら幸いです．

ここまで読んでいただきありがとうございました．

1. これらに加えてJordan標準形を習った人もいるでしょう． ↩

2. カーペレビッチと読みます． ↩

3. 行列要素を$T_{ij}$とかいたとき，任意の$i,j$について$\sum_{i=1}^dT_{ij}=1,\ \sum_{j=1}^dT_{ij}=1$，つまり任意の行和と列和が1となる非負行列のことです．二重確率行列は，一様分布$(1/d,1/d,\ldots,1/d)^{\mathsf{T}}$を変化させない性質を持ちます．Birkhoffの定理による美しい特徴づけは必見です．
   ちなみに，行和だけ1だと右確率行列，列和だけ1だと左確率行列といいます． ↩

4. 「ローレンツカーブ」と検索すると，一番上に総務省統計局のページが出てきます．また，経済学では「ジニ係数」などにmajorizationの考え方が用いられるようです． ↩

5. この説明は，沙川貴大先生のEntropy, Divergence, and Majorization in Classical and Quantum Thermodynamics,Springerを参照しました． ↩

6. Gershgorinとも書くそうです． ↩

7. こちらの簡潔な論文で簡略化されています． ↩