0. はじめに
本稿は,ギターエフェクトペダルの一種としてよく知られているフェイザーについて,その基本的な設計と実装方法について記述したものである.本稿では,まず,フェイザーというシステムの特徴と構成について簡単に述べる.次いで,フェイザーの主要な構成要素であるオールパスフィルタというシステムの特性について説明する.その後,オールパスフィルタとフェイザーの関係性について記述する.最後に,オーディオ信号処理に特化したプログラミング言語"Faust"を用いたフェイザーの実装例を示す.
1. フェイザーについて
フェイザーは,図1.1に示すように,そのゲイン線図上に複数のノッチを持つコムフィルタのようなシステムである.LFO等によってこれらのノッチの位置や幅を時間変化させることで,入力音を独特のうねりのある音へと変化させることができる.
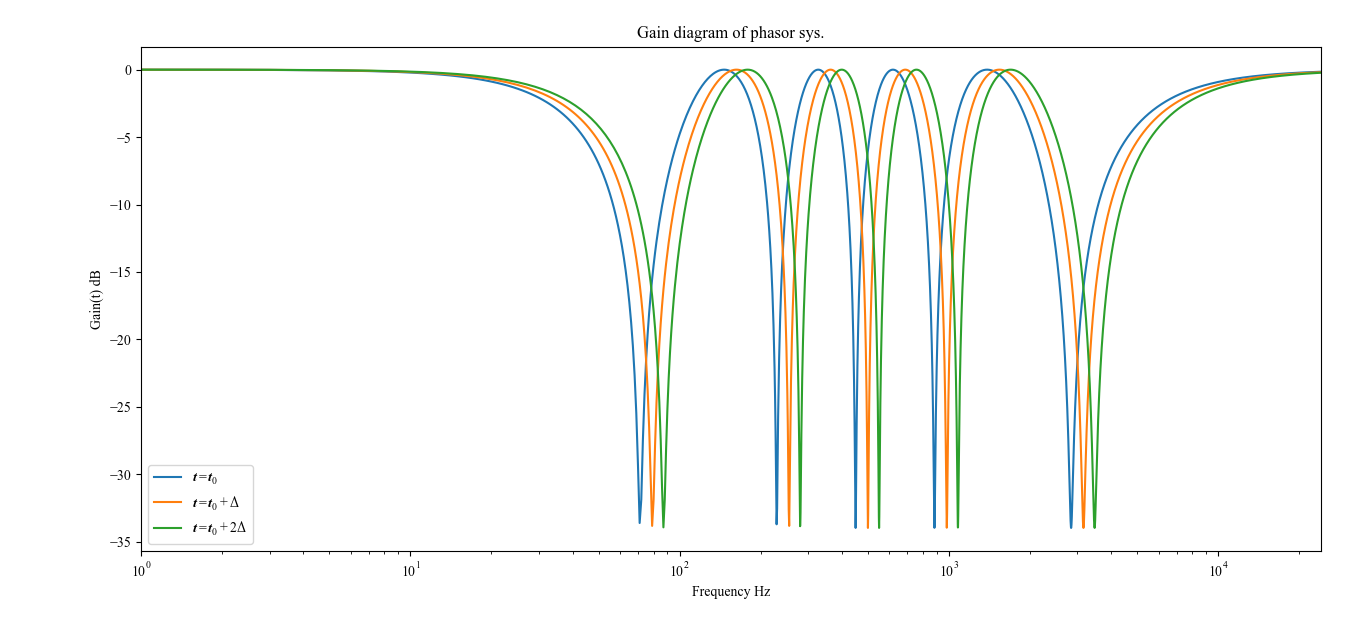
図1.1 フェイザーのゲイン特性のイメージ.$t$は時間を表す.
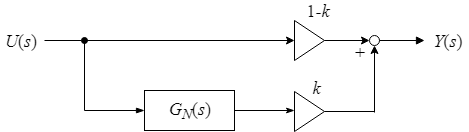
単純なフェイザーの構造は,図1.2に示すブロック線図で表される[1].
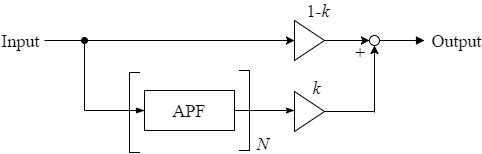
図2.1 フェイザーのブロック線図.APFは一次系オールパスフィルタ.$N$は偶数.$0 \leq k \leq 1$.
偶数個のオールパスフィルタを通過させたウェットな信号と,ドライな信号を混ぜ合わせることで図1.1に示したような複数のノッチが生じることになる.また,オールパスフィルタの数,フィルタ係数,ドライウェット比率を変化させることで,ノッチの数,位置,幅,深さを変化させることができる.
2. オールパスフィルタ
オールパスフィルタは入力信号の振幅には影響を与えず,位相のみを変化させるシステムであり,古典的な1次系のオールパスフィルタの伝達関数モデルとして式(2.1)が知られている[2].
G(s) = \frac{s - \omega_\mathrm{b}}{s + \omega_\mathrm{b}} \tag{2.1}
ここで,$G(s)$は1次系オールパスフィルタの伝達関数であり,$\omega_\mathrm{b} \ \mathrm{rad/sec}$はブレイク角周波数と呼ばれる値で,$0$より大きい実数をとるものとする.従って,式(2.1)で表されるシステムは安定である.このシステムのゲイン特性$g(\omega)
\mathrm{dB}$と位相特性$\phi(\omega)\ \mathrm{rad}$を計算すると次のようになる.
\begin{eqnarray}
g(\omega)&=& 20\log\sqrt{\mathrm{Re}(G(j\omega))^2 + \mathrm{Im}(G(j\omega))^2}\\
\\
&=& 0 \tag{2.2} \\
\\
\phi(\omega) &=& \arg G(j\omega)\\
\\
&=& \arg(j\omega - \omega_\mathrm{b}) - \arg(j\omega + \omega_\mathrm{b})\\
\\
&=& \pi - 2\tan^{-1}(\frac{\omega}{\omega_\mathrm{b}})\ \ \ \ (\omega \geq 0) \tag{2.3}
\end{eqnarray}
従って,式(2.1)で表されるシステムは,本節の冒頭で述べた"入力信号の振幅には影響を与えず,位相のみを変化させるフィルタである"というオールパスフィルタの性質を有することが確認できる.また,位相$\phi(\omega)$について,その群遅延$\tau_\mathrm{g}(\omega)$を次のように計算できる.
\begin{eqnarray}
\tau_\mathrm{g}(\omega) &=& -\frac{d\phi(\omega)}{d\omega}\\ \\
&=& \frac{2\omega_\mathrm{b}}{\omega_\mathrm{b}^{2} + \omega^2} \gt 0 \tag{2.4}
\end{eqnarray}
よって,位相$\phi(\omega)$は,$\omega \geq 0$の範囲で単調減少することがわかる.また式(2.3)と(2.4)より,位相$\phi(\omega)$については次のことも言える.
\begin{eqnarray}
\max \phi(\omega) &=& \pi \ \ \ \ (\omega = 0) \tag{2.5}\\\\
\min\phi(\omega) &=& 0 \ \ \ \ (\omega \to \infty) \tag{2.6}\\\\
\phi(\omega_b) &=& \frac{\pi}{2} \tag{2.7}
\end{eqnarray}
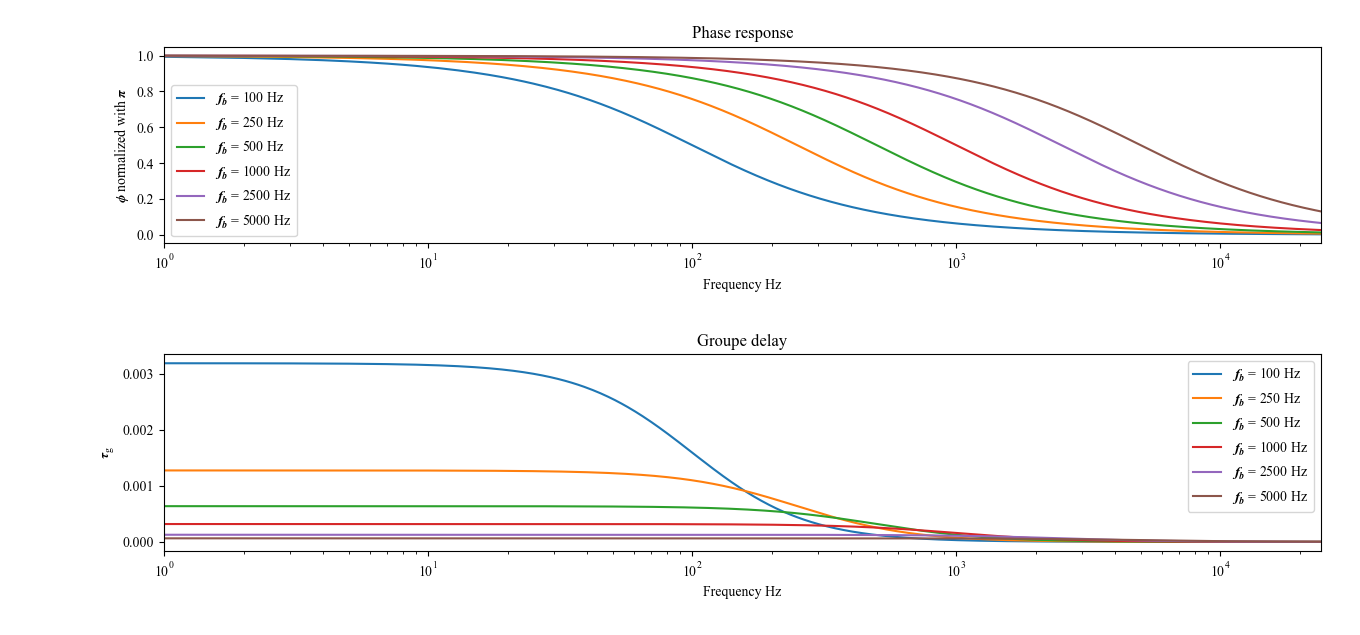
適当な$\omega_\mathrm{b}$について,$\phi(\omega)$と$\tau_\mathrm{g}(\omega)$をプロットしてみると次の図2.1のようになる.ここで,ブレイク周波数$f_\mathrm{b}$という値を操作量として導入し,$\omega_\mathrm{b} = 2\pi f_\mathrm{b}$と計算している(以降も作図の際には,この操作量を用いる).
図2.1からもわかるように,オールパスフィルタの位相特性と群遅延を表す関数の形状は,$\omega_\mathrm{b}$の値に影響を受ける.ただし,$\omega_\mathrm{b}$の値に依らず,式(2.4-7)は成立する.
続いて,フェイザーの構造にも見られる,複数のオールパスフィルタを直列に繋いだシステムについて考えていく.複数の線形時不変システムを直列に繋いでできるシステムのボード線図は,個々のシステムのボード線図の和で表現できるため,$N$個のオールパスフィルタを直列に繋いだシステム$G_N(s)$について,そのゲイン$g_N(\omega)$,位相$\phi_N(\omega)$及び群遅延$\tau_{\mathrm{g}, N}(\omega)$は次のようになる.
\begin{eqnarray}
g_N(\omega) &=& 0 \tag{2.8}\\\\
\phi_N(\omega) &=& N\phi(\omega) \tag{2.9}\\\\
\tau_{\mathrm{g}, N}(\omega) &=& N\tau_\mathrm{g}(\omega) \gt 0 \tag{2.10}
\end{eqnarray}
従って,位相$\phi_N(\omega)$については次のことも成り立つ.
\begin{eqnarray}
\max \phi_N(\omega) &=& N\pi \ \ \ \ (\omega = 0) \tag{2.11}\\\\
\min\phi_N(\omega) &=& 0 \ \ \ \ \ \ (\omega \to \infty) \tag{2.12}\\\\
\phi_N(\omega_b) &=& \frac{N\pi}{2} \tag{2.13}
\end{eqnarray}
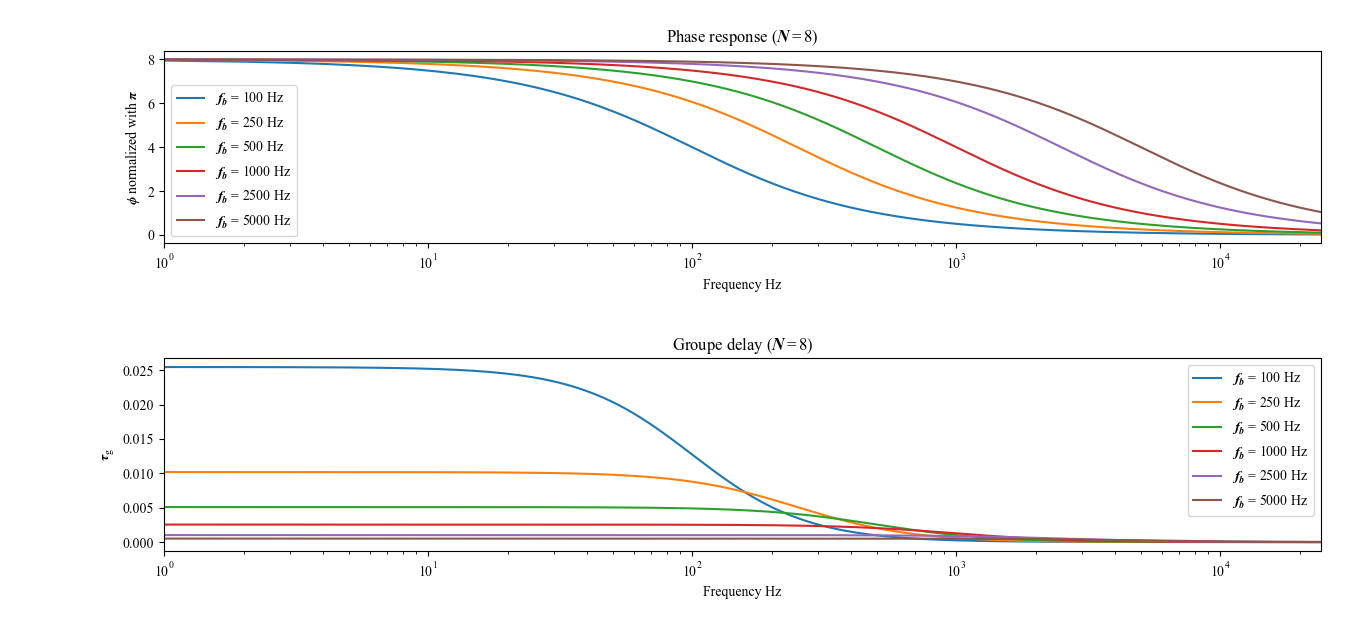
以上のことから,直列システムについても,$\phi_{N}(\omega)$と$\tau_{\mathrm{g}, N}(\omega)$の形状は,$\omega_\mathrm{b}$の値に影響を受けることになる.やはり,$\omega_\mathrm{b}$の値に依らず,式(2.11-13)も成立する(図2.2).
3. オールパスフィルタとフェイザー効果の関係
ここで,節2の内容を踏まえて,改めてフェイザーのブロック線図を示すと図3.1のようになる.
フェイザーの伝達関数を$G_{\mathrm{ph}}(s)$とすると,それは次のようになる.
\begin{eqnarray}
G_{\mathrm{ph}}(s) &=& kG_N(s) + (1-k) \tag{3.1}
\end{eqnarray}
ここで,$k$はドライウェット比率を表し,$0 \leq k \leq 1$の範囲をとるものとする.ここで,$G_{\mathrm{ph}}(s)$の振幅特性$|G_{\mathrm{ph}}(j\omega)|$は,次のように計算できる.
\begin{eqnarray}
|G_{\mathrm{ph}}(j\omega)| &=& |ke^{j\phi_N(\omega)} + (1-k)|\\\\
&=& \sqrt{k^2 + (1-k)^2 + 2k(1-k)\cos{\phi_N(\omega)}} \tag{3.2}
\end{eqnarray}
上記から,直列オールパスフィルタの位相$\phi_N(\omega)$がフェイザーの振幅特性に現れることになる.ここで,$k = 0, 1$の時は$|G_{\mathrm{ph}}(j\omega)| = 1$となるが,それ以外,すなわち$0 \lt k \lt 1$の時,次のことが言える.
\begin{eqnarray}
\max |G_{\mathrm{ph}}(j\omega)| &=& 1 \ \ \ \ (\cos\phi_N(\omega) = 1) \tag{3.3}\\\\
\min |G_{\mathrm{ph}}(j\omega)| &=& 2|k - 0.5|\ \ \ \ (\cos\phi_N(\omega) = -1) \tag{3.4}
\end{eqnarray}
ここで,前節にて$\phi_N(\omega)$は,$N\pi$から$0$に向けての単調減少関数であるとわかっている.従って,$N \geq 2$で,$\max |G_{\mathrm{ph}}(j\omega)|$と$\min |G_{\mathrm{ph}}(j\omega)|$が交互に繰り返し生じる,すなわち,図3.2のようにフェイザーの振幅特性$|G_{\mathrm{ph}}(j\omega)|$上にノッチが生じることになる.
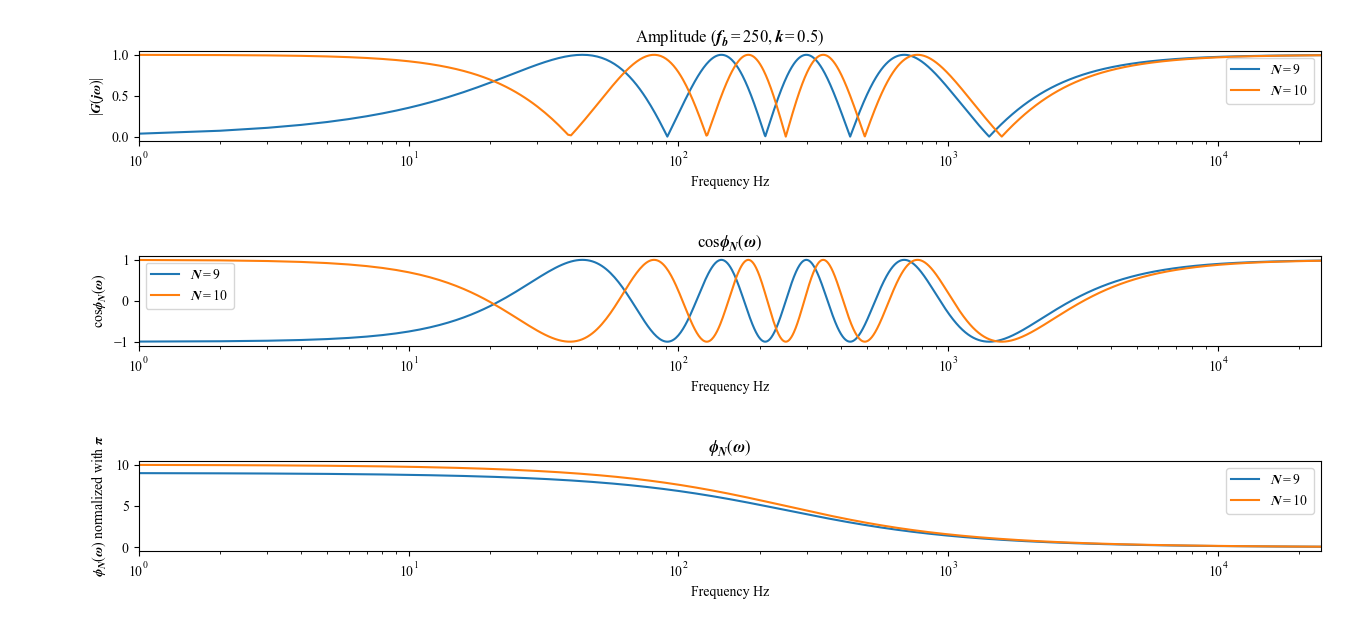
図3.2 直列オールパスフィルタの位相$\phi_N(\omega)$とフェイザーの振幅特性$|G_{\mathrm{ph}}(j\omega)|$の関係.
ノッチの数は$\cos\phi_N(\omega) = -1$の解の数に相当し,それの数は$2/N$となる.$N$が奇数の場合,低周波側にくる最初のノッチが不完全な形になってしまうため,オールパスフィルタの数$N$は偶数であることが望ましい.また,$\phi_N(\omega)$の形状は$\omega_\mathrm{b}$の値に影響を受けるため,$\omega_\mathrm{b}$を変化させることでノッチの位置と幅が変化することになる(図3.3).
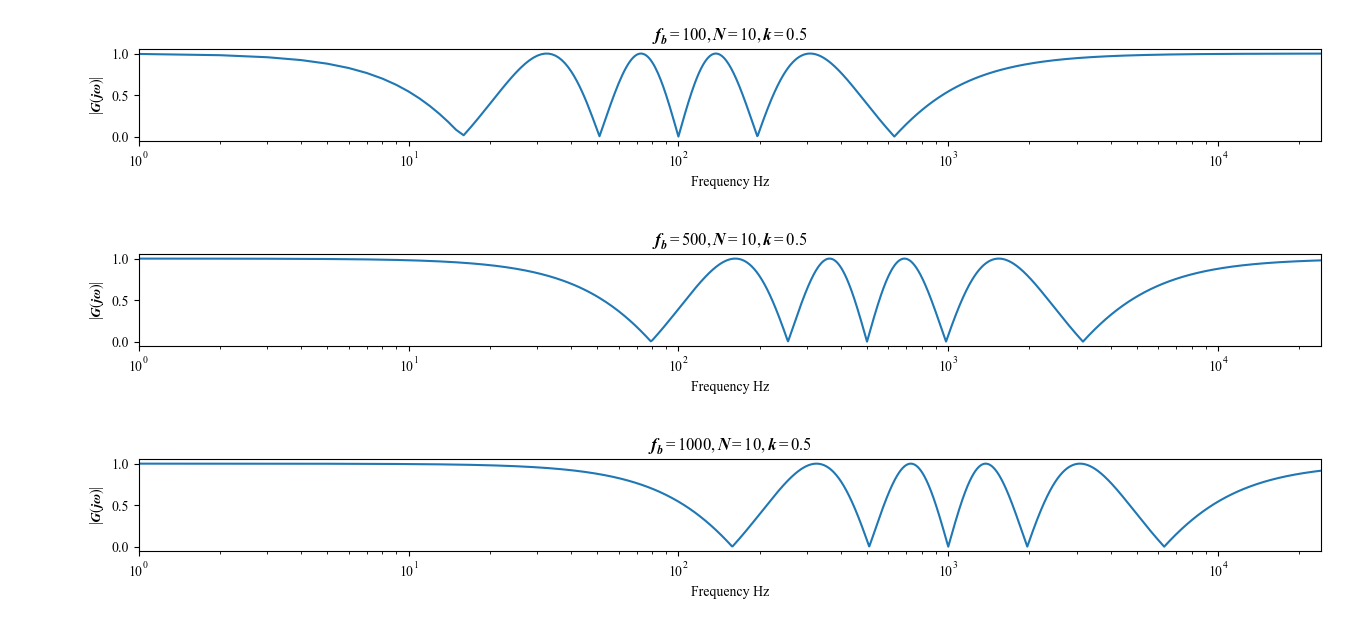
図3.3 ブレイク角周波数$\omega_\mathrm{b}$とフェイザーの振幅特性$|G_{\mathrm{ph}}(j\omega)|$の関係.
また,式(3.4)より,ドライウェット比$k$は,ノッチの深さを決める値であり,$k=0.5$の時に最もノッチが深くなることがわかる(図3.4).
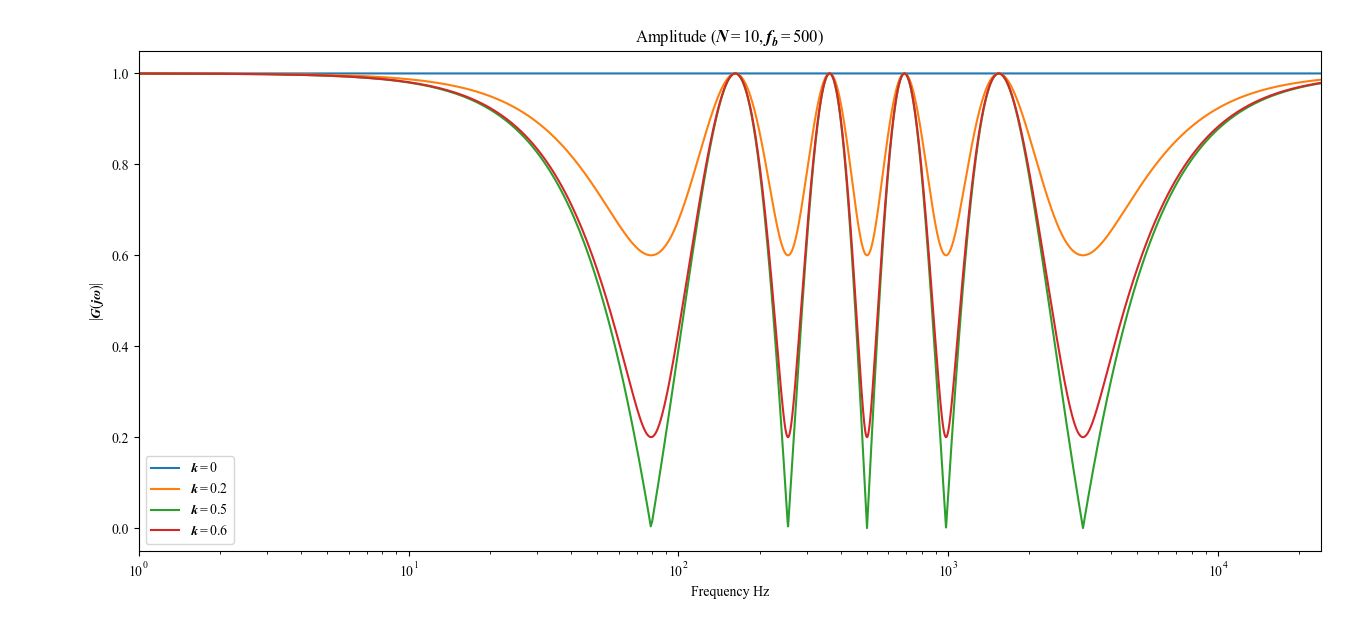
図3.4 ドライウェット比$k$とフェイザーの振幅特性$|G_{\mathrm{ph}}(j\omega)|$の関係.
以上をまとめると,フェイザーのノッチの数は直列させるオールパスフィルタの数$N$,ノッチの位置と幅はブレイク角周波数$\omega_\mathrm{b}$,ノッチの深さはドライウェット比$k$をパラメータとすることで,それぞれ独立に制御することができる.今回のように,1次系オールパスフィルタを用いた場合ではノッチの位置と幅の制御を独立させることはできないが,2次系のオールパスフィルタを用いればこれも可能である[3].
4. Faustによる実装例
オーディオ信号処理に特化したプログラミング言語"Faust"[Link]を用いて,フェイザーの実装を行う.コンピュータプログラムとして実装するにあたって,式(2.1)の伝達関数に対して,双一次変換を施した,式(4.1)のデジタル伝達関数$H(z)$をオールパスフィルタの伝達関数として実装にあてる.
H(z) = \frac{b_0 - z^{-1}}{1 - b_0z^{-1}}\ \ \ \ (b_0 = \frac{2f_\mathrm{s} - \omega_\mathrm{b}}{2f_\mathrm{s} + \omega_\mathrm{b}}) \tag{4.1}
以上を踏まえたフェイザーのサンプルコードを以下に示す.
import("stdfaust.lib");
//操作量
params = environment {
N_max = 12;
N = hslider("Number of APF", 2, 2, N_max, 1);
f_break = hslider("Break Frequency Hz", 440, 100, 5000, 0);
f_lfo = hslider("LFO frequency Hz", 1, 0.01, 5.0, 0);
amt_lfo = hslider("LFO amount", 0, 0, 1, 1);
mix = hslider("Dry/Wet", 0, 0, 1, 0);
outVol = hslider("Out volume", 0.2, 0, 1, 0);
};
//オールパスフィルタのフィルタ係数
b0(f_break) = (ma.SR - ma.PI*f_break) / (ma.SR + ma.PI*f_break);
//オールパスフィルタの伝達関数
apf(f_break, u) = (b0(f_break)*u - @(u, 1)) : + ~*(b0(f_break));
//直列オールパスフィルタ
cascade_apf = case{
(1, f_break, u) => apf(f_break, u);
(n, f_break, u) => apf(f_break, u)<:cascade_apf(n-1, f_break), _;
};
//直列数の可変
var_cascade_apf(N, f_break, u) = cascade_apf(N_max, f_break, u): ba.selectn(N_max, N_max-N)
with{
N_max = params.N_max;
};
//LFO
lfo(f, amt) = os.oscsin(f)*amt*250.0;
//Phasorの伝達関数
phasor(N, k, f_break, u) = u : k * var_cascade_apf(N, f_break), (1-k)*u : +;
//system全体の処理(mono)
mono_system(u) = abs(f_break + lfo(f_lfo, amt_lfo)), u : phasor(N, k), out: *
with {
f_lfo = params.f_lfo;
amt_lfo = params.amt_lfo;
f_break = params.f_break;
N = params.N;
k = params.mix;
out = params.outVol;
};
process = mono_system, mono_system;
5. おわりに
今回は,最小限の構成でのフェイザーシステムの設計についてのみ触れたが,直列オールパスフィルタの部分に負のフィードバック回路を持たせる等の拡張が一般によくある[1].また,節4に示したFaustコードは,オンラインコンパイラ[Link]等を利用すれば,手軽にVSTとしても出力できるため,ぜひ,実際にその出音を確認してみていただきたい...といいたいところなのですが,自分の場合はオンラインコンパイラから出力したVSTをReasonがうまく読み込まなかったので,一度,Jucerファイルとして出力してからVSTをビルドしました.
6. 参考文献
- R. Kiiski, F. Esqueda, V. Välimäki: Time-Variant Gray-Box Modeling of a Phaser Pedal, in Proc. 19th Int. Conf. Digital Audio Effects (DAFx-16), Brno, Czech,
Sep. 2016, pp. 31-38. [Link] - J. O. Smith, N. Lee: Time Varying Delay Effects [Online], 2008, Accessed 4 Feb. 2018.[Link]
- J. O. Smith: An allpass approach to digital phasing and flanging, in Proc. Int. Comp. Music Conf., Paris, France, Oct. 1984, pp. 103–109.[Link]