Python Matplotlibで基本的なグラフを書いてみる

はじめに

　こんにちは、この記事はPC初心者がプログラミングの勉強のために書いたものとなっています。予めご了承ください。今回は、Pythonの matplotlib を使用して基本的なグラフの書こうと思います。

開発環境

・Windows11
・Visual Studio Code
・Python 3.9.2
・matplotlib 3.4.3
・numpy 1.21.2

数式のグラフ化

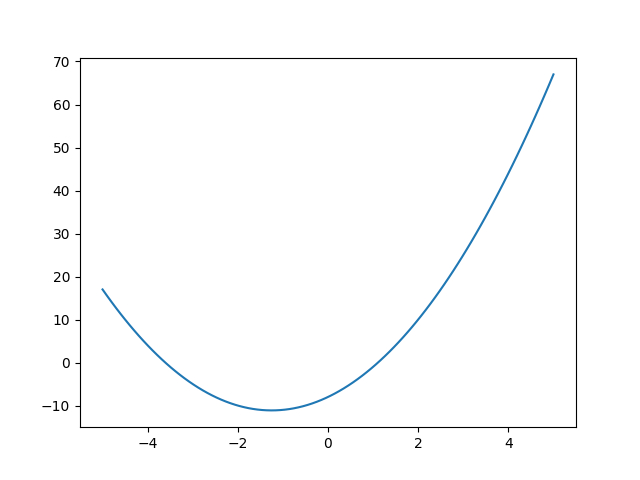
y = 2x^2 + 5x - 8 の数式を書いてみます。

コード

import matplotlib.pyplot as plt
import numpy as np
#ライブラリのインポート

# y = 2x^2 + 5x - 8 の数式を書く

x = np.linspace(-5, 5, 100)
# linespace 配列を書く
#第一引数: 最小値、第二引数: 最大値、第三引数: 分割数

y = 2*x**2 + 5*x - 8

plt.plot(x, y)

#対応する2つの配列の要素同士の点を結ぶ
plt.show()
#グラフの表示

出力

書けました。

散布図

scatter関数を使えば、散布図が書けます。
今回はsklearnにあるアヤメのデータを用いて散布図を書きます。

コード

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris
#ライブラリのインポート

iris = load_iris()
#アヤメのデータ

iris_data = pd.DataFrame(iris.data, columns=["sepal length(cm)", "sepal width(cm)", "petal length(cm)", "petal width(cm)"])
#アヤメのデータをデータフレームに格納
sep_len = iris_data["sepal width(cm)"]
#がく片の幅のデータ
pet_wid = iris_data["petal width(cm)"]
#花びらの長さのデータ

plt.scatter(sep_len,pet_wid)
#がく片の幅 と 花びらの長さ で散布図を書く
#scatter(xのデータ, yのデータ)

plt.xlabel("sepal width(cm)")
#x軸ラベル表示
plt.ylabel("petal width(cm)")
#y軸ラベル表示
plt.show()

出力

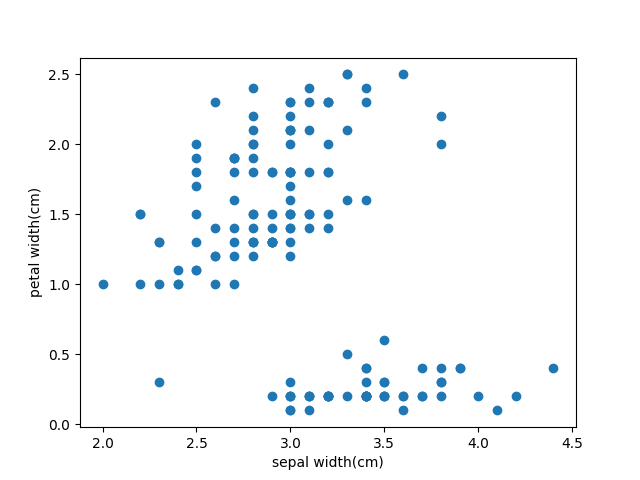
　sklearnライブラリに含まれるアヤメのデータをpandasを用いてデータフレームを作成しています。次に、そのデータから、「がく片の幅」と「花びらの長さ」を取り出しています。そして、二つのデータをscatter関数で散布図を作成しました。

棒グラフ

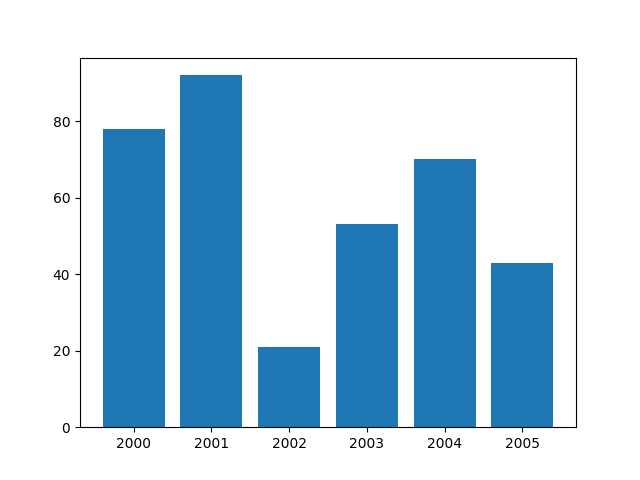
　bar関数で棒グラフが書けます。

コード

import matplotlib.pyplot as plt

left = [0,1,2,3,4,5]
#横軸の値(棒の数)
point = [78,92,21,53,70,43]
#縦軸の値
year = ["2000", "2001", "2002", "2003", "2004", "2005",]
#棒のラベル

plt.bar(left, point, tick_label=year)
#第三引数の tick_label には、棒のラベルを代入します。
plt.show()

出力

箱ひげ図

　箱ひげ図を作るには、boxplot関数を使います。ここでは、sklearnのデータセットに含まれている、3種のアヤメのsepal length(cm)で箱ひげ図を作成しました。

コード

import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_iris
#ライブラリのインポート

iris = load_iris()
#アヤメのデータ

iris_data = pd.DataFrame(iris.data, columns=["sepal length(cm)", "sepal width(cm)", "petal length(cm)", "petal width(cm)"])
#アヤメのデータをデータフレームに格納

setosa_sep_length = iris_data.loc[0:49, ["sepal length(cm)"]]
versicolor_sep_length = iris_data.loc[50:99, ["sepal length(cm)"]]
virginica_sep_length = iris_data.loc[100:149, ["sepal length(cm)"]]
#irisのデータには0~49行目までがsetosa種、50~99行目までがversicolor、
#100~149行目までがvirginica種のデータとなっている。
#loc カラム名で特定の行のデータを抽出

setosa_sepal_length = setosa_sep_length['sepal length(cm)'].to_list()
versicolor_sepal_length = versicolor_sep_length['sepal length(cm)'].to_list()
virginica_sep_length = virginica_sep_length['sepal length(cm)'].to_list()
#to_list シリーズをリストに変換

fig, ax = plt.subplots()
ax.set_title("iris sepal length")
ax.set_xticklabels(['setosa', 'versicolor','virginica'])
#set_xticklabels x軸の目盛に名前をつける(リストで渡す)
ax.set_ylabel("sepal length(cm)")
iris_sepal_length = (setosa_sepal_length, versicolor_sepal_length, virginica_sep_length)
bp = ax.boxplot(iris_sepal_length)
plt.show()

出力

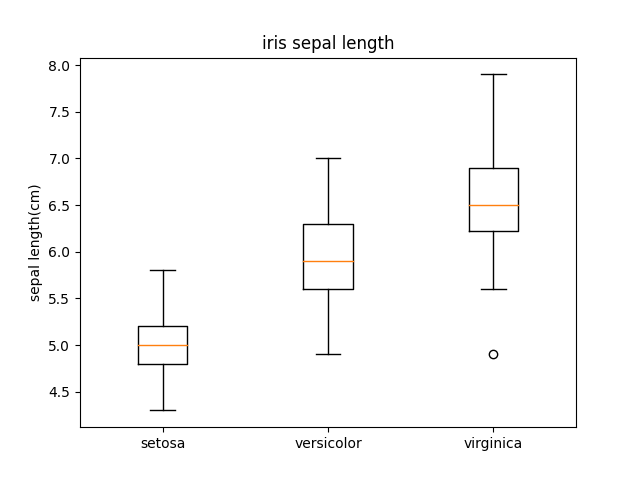
　まず初めに、アヤメのデータをデータフレームの変数に格納し、loc によって、インデックス・カラムを指定して、必要なデータ(今回はsepal length(cm))を抽出しています。抽出したデータはシリーズ型となっているため、これをリスト型に変換します*。そして、boxplot関数で箱ひげ図を作成します。なお、複数の箱ひげ図を描くときは、boxplot()にそれぞれのデータをタプル型で指定します。

*複数の箱ひげ図を描くとき、この操作をしないと、
ValueError: X must have 2 or fewer dimensions
というエラーが起こります。(シリーズ型だとインデックスが存在するせい?)

円グラフ

　pie関数で、円グラフが描けます。

コード

import matplotlib.pyplot as plt
import pandas as pd
import numpy as np

data = np.array([23, 34, 12, 5, 8, 18])
Name_list = {"Japan", "US", "USA", "Canada", "France", "Germany"}

fig = plt.figure()
#figure() グラフを表示する領域を作る 

ax1 = fig.add_subplot(1, 2, 1)
ax2 = fig.add_subplot(1, 2, 2)
#add_subplot() グラフを描く位置を追加 引数(行, 列, 場所)

ax1.pie(data)
ax1.set_title("before")
ax2.pie(data, labels=Name_list, startangle=90, counterclock=False
, autopct="%1.0f %%")
ax2.set_title("After")
plt.show()

出力

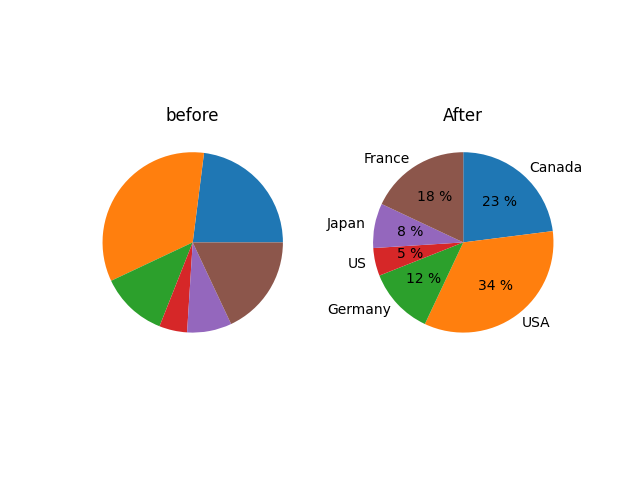
デフォルトのままでは見づらいので、pie関数の引数にいろいろ指定します。
startangle: グラフの開始位置を調整
counterclock: trueが指定されると時計回りにグラフが出力
autopct: 割合の値を表示

これで、見やすくなりました。

最後に

　今回は、よく使いそうなグラフである、座標平面・散布図・棒グラフ・箱ひげ図・円グラフの描き方を解説しました。各グラフを描く関数の引数を指定することで、様々な装飾も可能です。