本記事はN次元の物体の平行移動、回転移動をし、2次元に描画させる方法についてまとめていきます。
自分はこのような事は数日しかしていない全くの初心者なので、間違っているところがあると思います。そのような部分や分かりにくい点、曖昧な点を指摘してもらえると、とてもありがたいです。
0. 方針
3次元→2次元の関係から4次元→3次元を考えて、N次元に一般化していくようにやっていきます。
- 3DCGの技術を復習
- 4次元の物体を画面に描画するまでを考える
- N次元の物体を描画してみる
1. 3DCGの技術を復習
難しいので2つに分けて復習します。
- 平行移動や回転移動などの移動
- 物体をスクリーンに投影
1-1. 平行移動や回転移動などの移動
全ての点の座標は下のようなベクトルで表します。
\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}
最後の1は何なんだ？となりますが、今は放っといてください。
このベクトルと平行移動用の行列や回転移動用の行列などとの積で、この点を移動する事ができます。行列の掛け方は右、左とありますが、本記事では下のようにベクトルに左から行列を掛ける事とします。
\begin{pmatrix}
X \\
Y \\
Z \\
1
\end{pmatrix}
=
T
\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}
ここで行列の積という言葉が出てきて、ぎゃー！やめてー！と叫んでのたれ死ぬかもしれませんが、ベクトルと行列の積は簡単です。
\begin{align}
\begin{pmatrix}
X \\
Y \\
Z \\
1
\end{pmatrix}
&=
\begin{pmatrix}
a & b & c & 0 \\
d & e & f & 0\\
g & h & i & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix} \\
&=
\begin{pmatrix}
ax + by + cz \\
dx + ey + fz \\
gx + hy + iz \\
1
\end{pmatrix}
\end{align}
このように大変な計算は出てこないのでご安心ください。
平行移動
あるベクトルからベクトルtだけ、平行移動する行列です。
T_1=
\begin{pmatrix}
1 & 0 & 0 & t_x\\
0 & 1 & 0 & t_y\\
0 & 0 & 1 & t_z\\
0 & 0 & 0 & 1
\end{pmatrix}
これを実際に計算してみると左下のようになります。ここで4つ目の1の威力が発揮されます。これが無いと平行移動が出来ないのです！さて、なぜこれが無いと平行移動出来ないのでしょう？3*3の行列で色々試してみても、平行移動が出来ません。うーん、右下のように「tというベクトルと足し算すれば良いじゃ無いか。」と思いますが、他の全ての移動が掛け算で出来ているので、足し算を実装するのが綺麗では無いからこのようにしているのだと思います。
\begin{pmatrix}
x+t_x \\
y+t_y \\
z+t_z \\
1
\end{pmatrix}
=
T_1
\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}
\qquad
\begin{pmatrix}
x+t_x \\
y+t_y \\
z+t_z \\
\end{pmatrix}
=
\begin{pmatrix}
x \\
y \\
z \\
\end{pmatrix}
+
\begin{pmatrix}
t_x \\
t_y \\
t_z \\
\end{pmatrix}
さらにこの1を他の数にすると移動する尺度を変える事が出来ます。
\begin{pmatrix}
x+2t_x \\
y+2t_y \\
z+2t_z \\
2
\end{pmatrix}
=
T_1
\begin{pmatrix}
x \\
y \\
z \\
2
\end{pmatrix}
拡大・縮小
あるベクトルにそれぞれの要素にsを掛けて、拡大・縮小します。
T_2=
\begin{pmatrix}
s_x & 0 & 0 & 0\\
0 & s_y & 0 & 0\\
0 & 0 & s_z & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
回転行列
あるベクトルをx,y,z軸周りに $\theta$ だけ回転させます。他にもクォータニオンやオイラー角などがありますが、行列がN次元の場合に最も使いやすいので取り扱いません。
T_x=
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & \cos \theta & -\sin \theta & 0\\
0 & \sin \theta & \cos \theta & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\qquad
T_y=
\begin{pmatrix}
\cos \theta & 0 & -\sin \theta & 0\\
0 & 1 & 0 & 0\\
\sin \theta & 0 & \cos \theta & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\qquad
T_z=
\begin{pmatrix}
\cos \theta & -\sin \theta & 0 & 0\\
\sin \theta & \cos \theta & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
これらを掛け合わせる事で3次元のどんな移動も出来ます。
1-2. 物体をスクリーンに投影
色々な方法がありますがここではこの2つ紹介します。正規化などは今回の主題とは関係ないので話しません。
- 平行投影
- 透視投影
平行投影
めちゃくちゃ簡単です。x,y座標だけを取り出してそのまま表示します。これは人間が物体を見るときに起きる遠近感を全て無視するので、遠いものと近いものは同じ大きさとして表示されます。行列で表現するとこのような感じです。
\begin{pmatrix}
x \\
y \\
\end{pmatrix}
=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}
透視投影
人間の遠近感を作る為の投影です。ゲームなどで普段使われる投影方法はこちらです。カメラの位置と原点の距離をRとして、それらから出来る三角形は相似の形をしているからこのように表現出来ます。今回はこれを使ってN次元の投影します。
v = \frac{R}{R-z} \\
\begin{pmatrix}
x' \\
y' \\
z' \\
1
\end{pmatrix}
=
\begin{pmatrix}
v & 0 & 0 & 0 \\
0 & v & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z \\
1
\end{pmatrix}
2. 4次元の物体を画面に描画するまでを考える
2-1. 4次元ってそもそも何？
0次元は点、1次元は線、2次元は面、3次元は立体。じゃ4次元は何でしょうか。
今までユークリッド幾何学で知った知識をそのまま言葉にすると、
「直行する4つの軸からなる空間。」
...と言われても全然しっくりきませんね。
具体的に4次元のものを3次元に投影したものを見せます。
ボンッ！
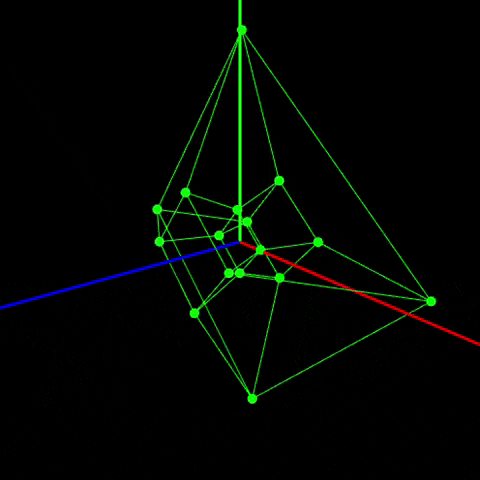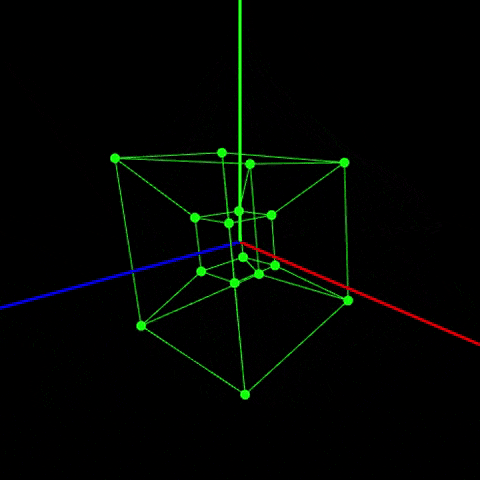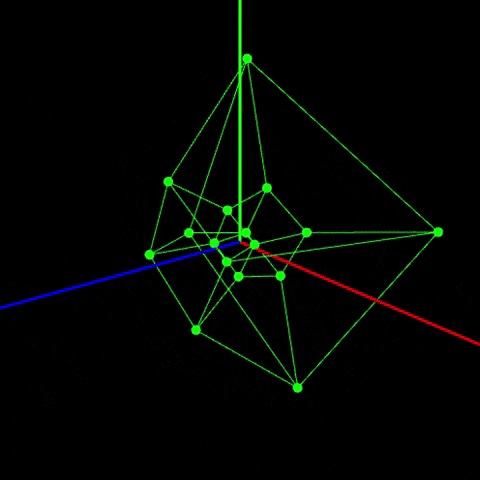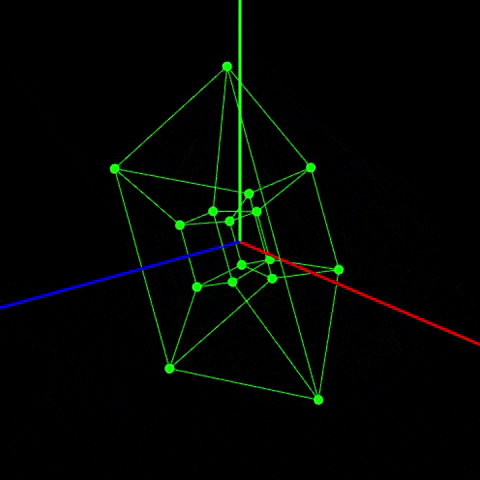これが正八胞体の回転です！！！興奮しませんか？僕は興奮してます！やばいですよね！
はい、正八胞体と呼ばれるように4次元では胞と呼ばれます。回転しているだけなので4次元で言う体積は変わっていません。もっと見てみましょう！
ボンボンッ！
正五胞体
正十六胞体
これが4次元ですよ！4次元感じてますよ！！！
これらを描画出来るようにしていきましょう！
2-2. 4次元の移動・投影
ここからは少し難しくなるので平行移動は考えない事にします。なので点は左下のようなベクトルで、右下のように移動させます。
\begin{pmatrix}
x \\
y \\
z \\
w
\end{pmatrix}
\qquad
\begin{pmatrix}
X \\
Y \\
Z \\
W
\end{pmatrix}
=T
\begin{pmatrix}
x \\
y \\
z \\
w
\end{pmatrix}
拡大・縮小
T=
\begin{pmatrix}
s_x & 0 & 0 & 0\\
0 & s_y & 0 & 0\\
0 & 0 & s_z & 0\\
0 & 0 & 0 & s_w
\end{pmatrix}
回転行列
3次元では回転の自由度は3でしたが、4次元では自由度は6あります。最初の3つがカッコいい(?)回転で後の3つがx,y,z軸周りの回転です。
T_{xy}=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & \cos \theta & -\sin \theta \\
0 & 0 & \sin \theta & \cos \theta \\
\end{pmatrix}
\qquad
T_{yz}=
\begin{pmatrix}
\cos \theta & 0 & 0 & -\sin \theta\\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
\sin \theta & 0 & 0 & \cos \theta \\
\end{pmatrix}
\qquad
T_{xz}=
\begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & \cos \theta & 0 & -\sin \theta \\
0 & 0 & 1 & 0 \\
0 & \sin \theta & 0 & \cos \theta \\
\end{pmatrix}
T_{xw}=
\begin{pmatrix}
1 & 0 & 0 & 0\\
0 & \cos \theta & -\sin \theta & 0\\
0 & \sin \theta & \cos \theta & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\qquad
T_{yw}=
\begin{pmatrix}
\cos \theta & 0 & -\sin \theta & 0\\
0 & 1 & 0 & 0\\
\sin \theta & 0 & \cos \theta & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
\qquad
T_{zw}=
\begin{pmatrix}
\cos \theta & -\sin \theta & 0 & 0\\
\sin \theta & \cos \theta & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1
\end{pmatrix}
透視投影
4次元の物体を3次元に投影します。更にもう一度、3次元の透視投影を行う事でスクリーンに写すことが出来ます。計算は先ほどと殆ど同じですね。
v = \frac{R}{R - w}
\begin{pmatrix}
x' \\
y' \\
z' \\
\end{pmatrix}
=
\begin{pmatrix}
v & 0 & 0 & 0 \\
0 & v & 0 & 0 \\
0 & 0 & v & 0 \\
\end{pmatrix}
\begin{pmatrix}
x \\
y \\
z \\
w
\end{pmatrix}
正八胞体の回転のプログラム
ここまで数学の式をコネコネしてきましたけど、これで本当に表示出来るの？と思ったので、簡単に正八胞体の回転をやってみます。ここではProcessing, P3Dを使います。言語はJavaです。
float[][] cell8 = {
{-1,-1,-1,-1},
{-1,-1,-1,1},
{-1,-1,1,-1},
{-1,1,-1,-1},
{1,-1,-1,-1},
{-1,-1,1,1},
{-1,1,-1,1},
{1,-1,-1,1},
{-1,1,1,-1},
{1,-1,1,-1},
{1,1,-1,-1},
{-1,1,1,1},
{1,-1,1,1},
{1,1,-1,1},
{1,1,1,-1},
{1,1,1,1},
};
void setup() {
size(500, 500, P3D);
background(0);
noFill();
}
void draw() {
background(0);
camera(200, -180, 200, 0, 0, 0, 0, 1.0, 0);
stroke( 0, 255, 0 );
strokeWeight(10);
for (float[] point: cell8){
// 拡大 & 透視投影 & 描画
float w = 50 / (2.0 - point[3]);
point(-w*point[0], -w*point[1], -w*point[2]);
}
// XY軸の回転
for (float[] point: cell8){
float[] rot = rotationXY(point, 0.05);
for (int i = 0; i < rot.length;i++) {
point[i] = rot[i];
}
}
}
float[] rotationXY(float[] point, float rad) {
float[][] rotXY = {
{1,0,0,0},
{0,1,0,0},
{0,0,cos(rad),-sin(rad)},
{0,0,sin(rad),cos(rad)}
};
return matmul(point, rotXY);
}
float[] matmul(float[] vec, float[][] mat) {
float[] ans = {0,0,0,0};
for (int i = 0; i < mat.length; i++) {
for (int j = 0; j < mat[i].length; j++) {
ans[i] += vec[j] * mat[i][j];
}
}
return ans;
}
このようなプログラムを書けば、最初に見たようなカッコいい図形が表示されるはずです！
3. 更にその先へ
やっとN次元物体です！と言っても今までのように普通に拡張すれば良いです。N次元の回転の自由度は$n(n-1)/2$です。
N次元座標の行列表示
\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
ベクトルの移動
\begin{pmatrix}
X_1 \\
X_2 \\
\vdots \\
X_n
\end{pmatrix}
=T
\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
拡大・縮小
T=
\begin{pmatrix}
s_{x_1} & & \cdots & & 0\\
& \ddots & & & \\
\vdots & & s_{x_i} & & \vdots \\
& & & \ddots & \\
0 & & \cdots & & s_{x_n}
\end{pmatrix}
回転行列
T=
\begin{pmatrix}
1 & & & \cdots & & & 0\\
& \ddots & & & \\
& & \cos \theta & \cdots & -\sin \theta & & \\
\vdots & & \vdots & \ddots & \vdots & & \vdots \\
& & \sin \theta & \cdots & \cos \theta & & \\
& & & & &\ddots \\
0 & & & \cdots & & & 1 \\
\end{pmatrix}
透視投影
v = \frac{R}{R - x_n}
\begin{pmatrix}
x_1' \\
x_2' \\
\vdots \\
x_{n-1}' \\
\end{pmatrix}
=
\begin{pmatrix}
v & & & 0 \\
& \ddots & & \\
0 & & v & 0 \\
\end{pmatrix}
\begin{pmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{pmatrix}
おーし、6次元立方体の回転とかどんなのになるのかな〜
ドンッ！
っ6次元キューブじゃ！
— あんこ₍₍⁽⁽⊂(。^∀^)⊃₎₎⁾⁾ (@Anko_9801) 2019, 7月 28
おおおおお！！！
これらはProcessingを使って描画しました。ソースコードは上がっているので、もしよかったら見ていってください。