【機械学習で音声認識や音声分析をしたい人におすすめ】
— あんはる@準優勝 アプリ甲子園 (@_anharu) November 8, 2020
音声特徴量であるMFCCを理解するために重要だった「声の生成の仕組み」
図をたくさん自分で作ってわかりやすく説明してみたので
是非読んでいただきたいです🙇♀️
音声特徴量の理解に役に立つ、声の生成の仕組み https://t.co/b2UwUj9znP #Qiita
現在、男性と女性の音声を分類するという研究をしています。
MFCC（メル周波数ケプストラム係数）を用いて学習させるとうまくいきました。
しかし、MFCCとはなんなのだろうか、どうやって"人の聴覚特性を考慮している特徴量"が作られているのだろうかというのが知りませんでした。
それを調べたところ、声の生成の仕組みが密接に関わっているので取り上げていきたいと思います。
音声分析の方法
複雑な波形は正弦波や余弦波の和として表せる場合があります。それは、フーリエ変換をすることで構成する角周波数、振幅の三角関数を求めることができます。そして、横軸をそこで得られた三角関数の周波数、縦軸を振幅で表したものをスペクトルと言います。
https://ja.wikipedia.org/wiki/フーリエ変換 から引用↓
わかりやすいアニメーション（複雑な波->構成する三角関数->スペクトルのグラフ）
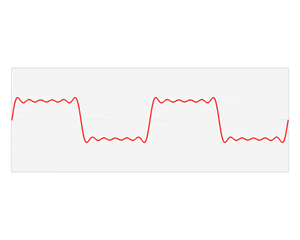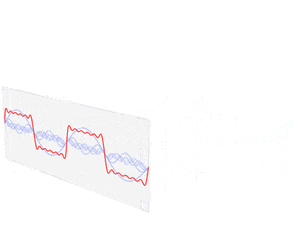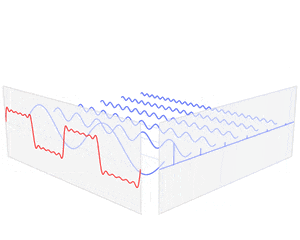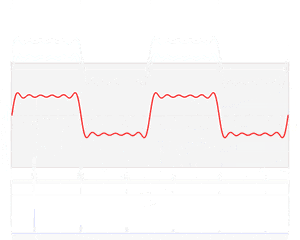
音声分析では、音声の波形をフーリエ変換を得られたスペクトルの特徴を使います。
また、パワースペクトル（振幅の二乗）や対数パワースペクトル（振幅の二乗の常用対数をとったもの）もよく用いられます。
声の生成の仕組み
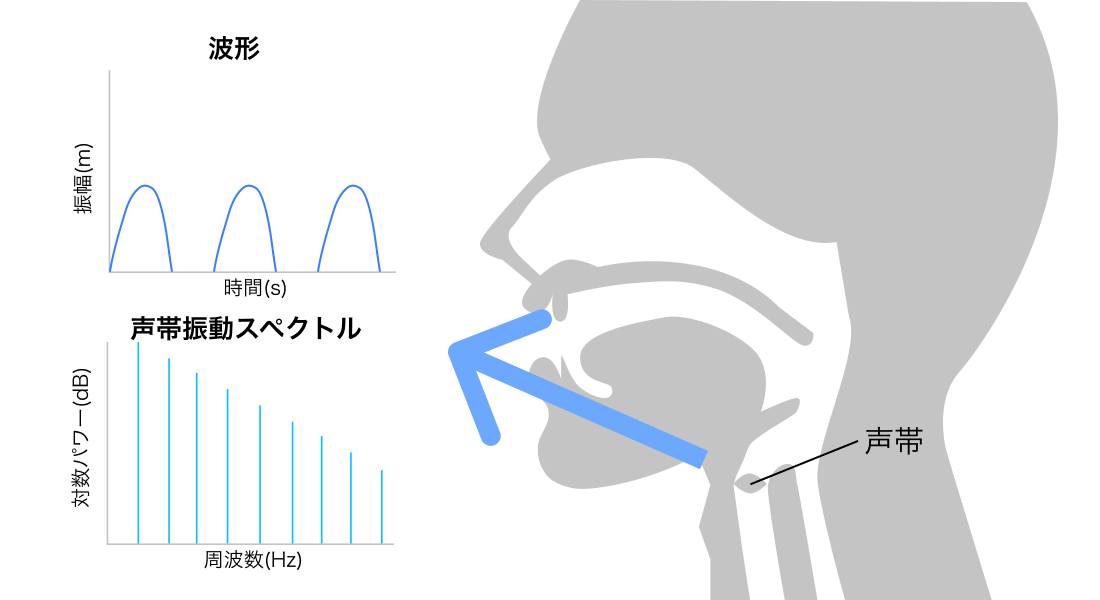
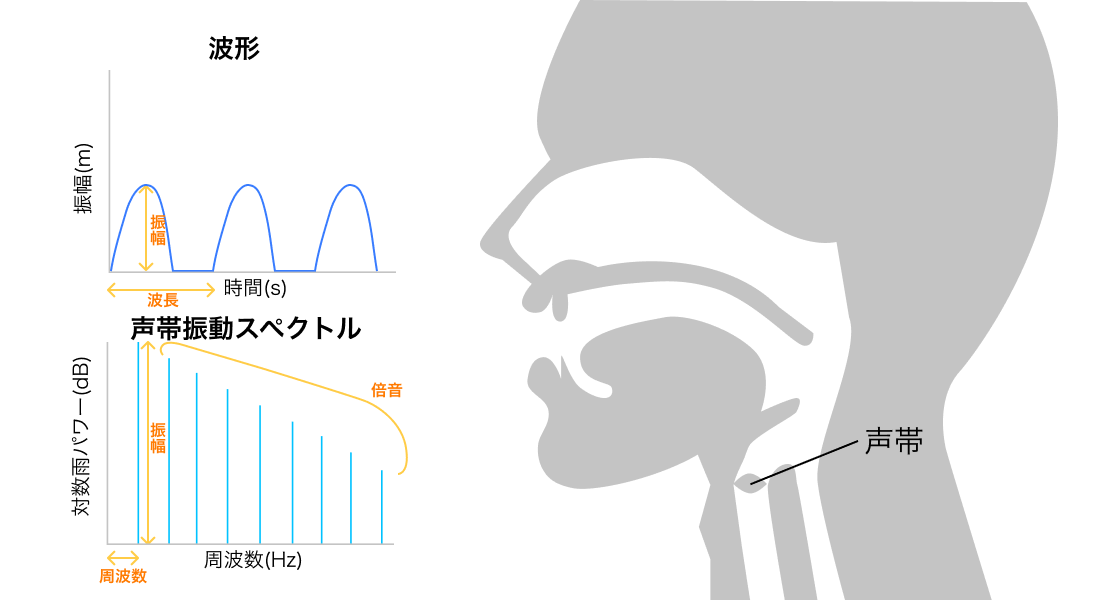
空気が肺から気管を通って、声帯で振動し、声道で振動して"声"ができます。
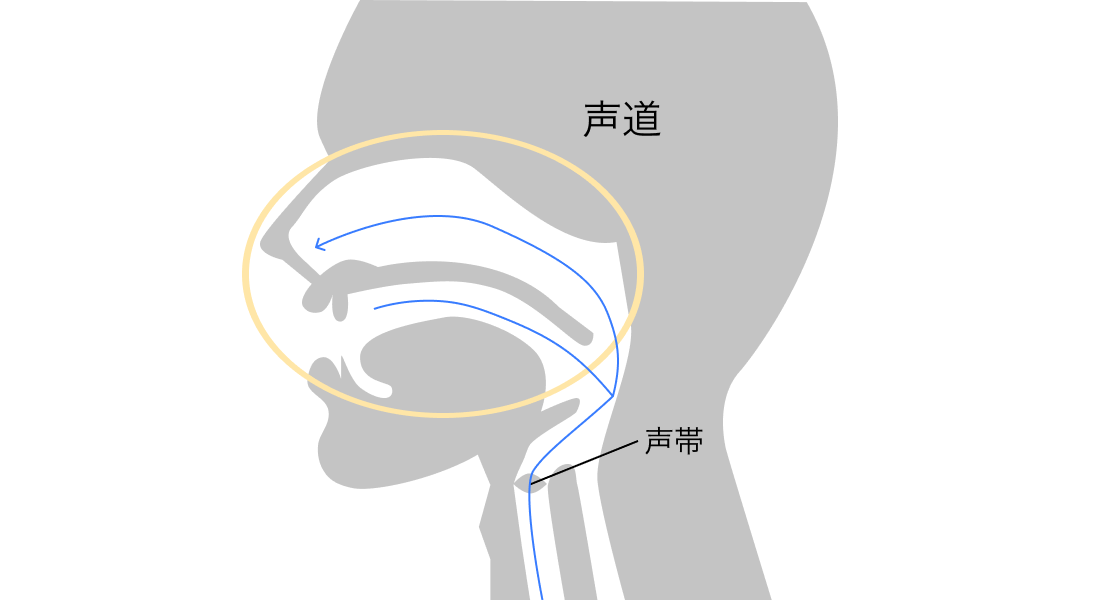
声帯での振動
空気が肺から気管を通り、声帯で振動します。
波形は純音に近く、一定の周波数と振幅を持っています。
つまり、一定の周波数と振幅を持つということは、音の高さと大きさが決まるということです。
男女や年齢によって声帯の長さが違うので差が出ます。
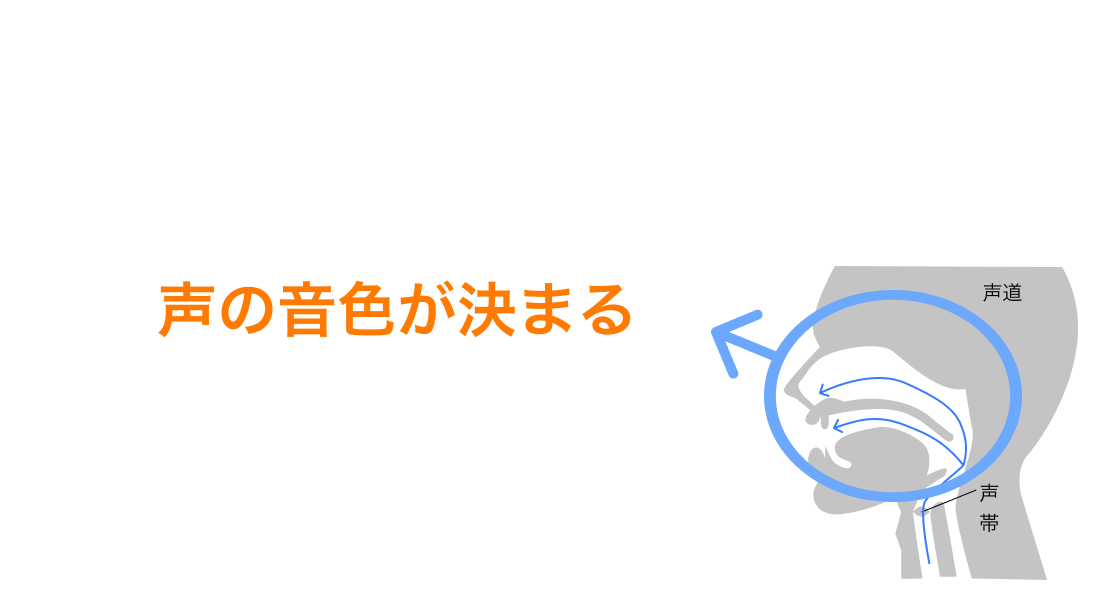
声道での共鳴
そして声道と呼ばれる、口腔や鼻腔の空間で空気は共鳴します。
そうすることで音声の波形ができます。
音声波形は、声帯振動の波形を声道フィルタで畳み込みすることで導き出せます。
"畳み込み"とは、ある関数に平行移動しながらある関数を重ね足し合わせる操作です。
https://ja.wikipedia.org/wiki/畳み込み から引用、畳み込みのアニメーション
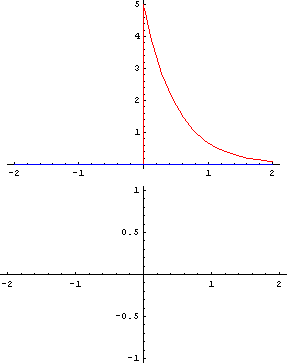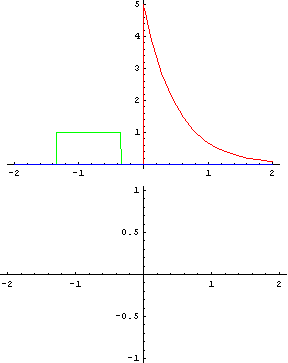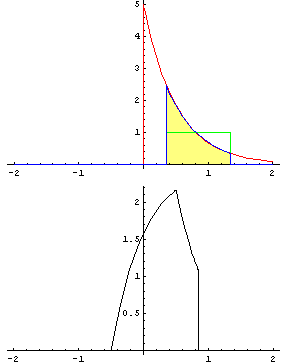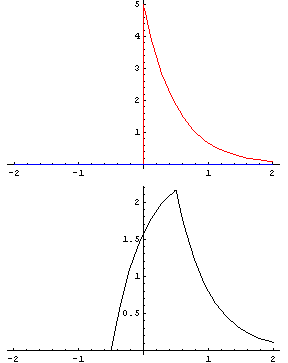
畳み込みによって、このような波形ができます。
なので、声帯振動パワースペクトルと声道パワースペクトルの掛け算として表されます。
そうすると、声帯振動対数パワースペクトルと声道対数パワースペクトルの足し算として表すことができます。
これは、音声特徴量である、ケプストラムやMFCC（メル周波数ケプストラム係数）へ繋がっていきます。（また記事を書くつもり）
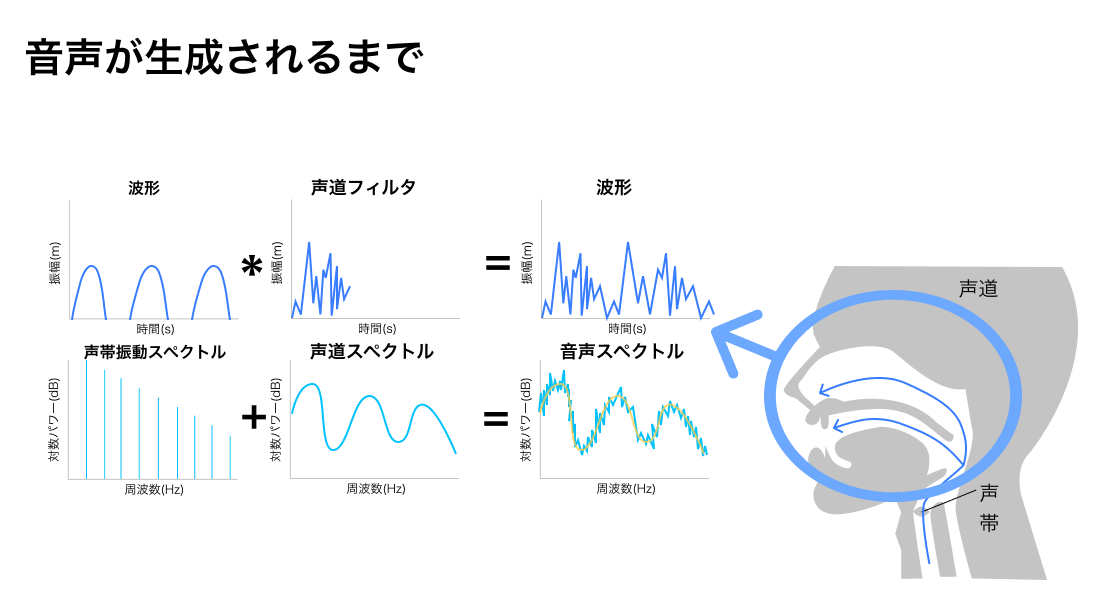
よって、声道フィルタに通ることで、声の音色が決まります。
音声認識・分類をするには？
上の説明を見て気づいた方もいるかもしれませんが、音声スペクトルをフーリエ変換すると、高周波帯は声帯振動の成分、低周波の成分は声道の成分に分けられることができます。（ここで得られたものはケプストラム）
つまり、"声の高さ・大きさ"の特徴量と、"声の音色"の特徴量に分けることができるのです。
そして、声の音色"の特徴量が重要で発音に関わるので音声認識に利用されています。
ケプストラムを加工してより"人の聴覚特性を考慮している特徴量"として使われているのがMFCC（メル周波数ケプストラム係数）です。
次の記事ではそれについて説明したいと思います。