高速フーリエ変換・数論変換を改めて理解しようという話

本記事は，eeic（東京大学工学部電気電子・電子情報工学科） Advent Calendar 2022 の 12 月 21 日ぶんの記事です．

はじめに

本記事は，高速フーリエ変換（ Fast Fourier Transform. 以下，本記事では「FFT」と略すことがあります）や数論変換（ Number Theorem Transform．以下，本記事では「NTT」と略すことがあります）の原理およびその実装・そしてその応用について述べる記事です．¹

近年，競技プログラミングで FFT・NTT を必要とする問題の出題がかなり増えています．出題頻度が増えたことによって解く人も増えてきており，もはや競技プログラミングの上達を目指す上では FFT・NTT を使えるようにすることは避けては通れない道となっているのが現状です．

しかし，FFT・NTT は，かなり理解が大変な難しいアルゴリズムとして知られています．著者も，FFT・NTT を最初に学んだときにはとても時間がかかったことを覚えています．そのこともあってか，FFT・NTT の理解に悩まされている人も多いことかと思います．

さらに，ACL（AtCoder Library）²が登場したことにより，基本的な NTT での演算を行う場合は自分で実装せずとも， atcoder::convolution を呼び出すだけで出来てしまいます．したがって，簡単な NTT の問題ならばその中身を理解せずとも使えるようになってしまっているのが現状です．

とは言え，原理を理解することの意味がなくなったわけでは全くもってないと考えています．競技プログラミングでは，アルゴリズムを知っているだけではなく，それをどのように応用させて使うかが問われることが多いです．そのためには，アルゴリズムへの深い理解が必要とされます．FFT・NTT もその例外ではなく，原理を知っていることでそのアルゴリズムへの理解が深まり，その応用も出来るようになっていくと考えています．

この記事では，高速フーリエ変換や数論変換について，原理から実装までの基礎的な部分の説明を行うことで，その理解を深めることを目標とします．さらに，実際の問題でどのように FFT や NTT が用いられるかについても，取り上げます．

なお，説明中のコードは全て C++ を使っています．ご了承ください．

1. 多項式乗算

今回の記事で目標とするのは，次のような多項式乗算を高速に行うことです．

$n$ 次の多項式 $A(x)=A_0 + A_1x + A_2x^2 + \cdots + A_nx^n$ と，$n$ 次の多項式 $B(x)=B_0 + B_1x + B_2x^2 + \cdots + B_nx^n$ が与えられたとき，それを掛け合わせた多項式 $C(x)=C_0 + C_1x + C_2x^2 + \cdots + C_{2n}x^{2n}$ を求める．

言い換えると，長さ $n+1$ の配列 $A=(A_0, A_1, A_2, \cdots , A_n)$ と，長さ $n+1$ の配列 $B=(B_0, B_1, B_2, \cdots, B_m)$ が与えられたとき，この 2 つの配列に対して，$C_i=\sum_{i = j + k}A_jB_k$ によって定められる配列 $C=(C_0, C_1, C_2, \cdots, C_{2n})$ を求める．

実際には，2 つの多項式の次数は異なる場合もありますが，その場合は係数を $0$ で埋めることで次数を合わせればよいです．これは，以下のようなコードで計算すれば求まりますが，計算量は $ \Theta (n^2)$ となってしまい，$n$ が大きいとかなり遅いです．

for (int j = 0; j <= n; j++){
    for (int k = 0; k <= n; k++){
        C[j + k] += A[j] * B[k];
    }
}

これを，より良い計算量で解く，というのが今回の目標です．

2. 多項式乗算をより良い計算量で行う作戦

FFT・NTT に移る前に，どのようにして高速に多項式乗算を行うのかについて方針を述べます．

愚直解法では多項式を直接掛け算する，ということを行いましたが，それでは計算量の高速化は難しそうです．そこで，方針を変換し，結果となる多項式の係数を何かしらの方法で求める，という方針を取ることにしましょう．

ここで用いるのが，次に示す多項式補間です．

$m$ 次の多項式 $f(x)=c_0+c_1x+\cdots+c_mx^m$ は，$m+1$ 個の異なる $x_i$ とそれに対応する $f(x_i)$ の組，$((x_0, f(x_0)), (x_1, f(x_1)), \cdots, (x_m, f(x_m))$ がわかっていれば，必ず一意に定まる．

これにより，$m+1$ 個の異なる $x_i$ と，それに対応する $f(x_i)$ の値の組を何かしらの方法で計算し，その結果を利用して元々の多項式の係数 $c_0, c_1, \cdots, c_m$ を求める，という方針を取ることができます．

例を挙げましょう．$f(x)=c_0+c_1x+c_2x^2$ に対して，$f(0)=2,f(1)=1, f(3)=5$ が成り立っているとします．そうすると，これらを $f(x)=c_0+c_1x+c_2x^2$ に代入することで，

• $c_0 = 2$
• $c_0+c_1+c_2=1$
• $c_0+3c_1+9c_2=5$

がわかります．これは $c_0,c_1,c_2$ についての連立方程式となっており，これを解くことで $c_0=2,c_1=-2,c_2=1$ を得ることができ，$f(x)=2-2x+x^2$ を得られます．

元の問題にこれを適用することを考えましょう．$C(x)=A(x)B(x)$ であることから，$x_i$ に対して $A(x_i), B(x_i)$ の値がわかっているならば，$C(x_i)=A(x_i)B(x_i)$ と，$C(x_i)$ の組の計算ができるため，結局掛け合わせる前の多項式 $A(x),B(x)$ に対して $A(x_i), B(x_i)$ の組の計算ができればよいことになります．また，$C(x)$ の次数は $2n$ であることから，少なくとも $2n+1$ 個の異なる $x_i$ について計算を行う必要があります．

とは言え，$A(x_i), B(x_i)$ の組の計算は全部愚直にやると $O(n^2)$ かかり，また $C(x_i)$ から $C(x)$ を求めるのは $(2n+1)$ 個の連立方程式を解くことが必要となるため，愚直にやると $O(n^3)$ かかってしまいます³．そのため，「$f(x_i)$ の組の計算」と「多項式の係数を求める」を何かしらの方法で工夫して行う必要があるわけです．

まとめると，多項式乗算をより良い計算量で行う作戦は次の通りです．

• 何かしらの工夫を行って $2n+1$ 個の $x_i$ を選び，それに対応する $A(x_i), B(x_i)$ を求める．
• 求めた $A(x_i),B(x_i)$ に対して，$C(x_i)=A(x_i)B(x_i)$ を計算する．（これは $O(n)$ で計算可能なので，愚直にやって問題ありません）
• 何かしらの工夫を行って $C(x_i)$ から $(C_0, C_1, \cdots, C_{2n})$ を求める．

3. 1 の N 乗根の性質について

早速2節で述べた「作戦」について述べていきたいところですが，その前に準備として，この先の議論で必要となる数学的な議論を行います．

3-1. 1 の N 乗根

$N$ 乗すると $1$ になる数を，$1$ の $N$ 乗根 と言います．$1$ の $N$ 乗根は全部で $N$ 個あり，$\cos{\frac{2πk}{N}} + i\sin{\frac{2πk}{N}}=e^{i\frac{2πk}{N}}(0 \leq k < N)$⁴ のように表されます（ただしここでの $i$ は虚数単位を表します）．以下，$e^{i\frac{2π}{N}}=\zeta_N$ とおきます．

3-2. 1 の N 乗根の性質

$1$ の $N$ 乗根には，以下のような性質があります．

• $(\zeta_N)^{N}=1$
• $(\zeta_N)^{0}, (\zeta_N)^{1}, (\zeta_N)^{2}, \cdots, (\zeta_N)^{N-1}$ はすべて異なる．
• $\sum_{k=0}^{N-1}(\zeta_N)^{kl}$ は $l \equiv 0 \pmod N $ のとき $N$，そうでないとき $0$ である．

一番下の性質の証明：$l \equiv 0 \pmod N $ のとき，$(\zeta_N)^{kl}=1$ なので，$\sum_{k=0}^{N-1}(\zeta_N)^{kl}=N$．そうでないとき，$(\zeta_N)^{kl}=((\zeta_N)^{l})^{k}$ であることから，等比級数の和の公式を用いると，$\frac{1 - (\zeta_N)^{ln}}{1 - (\zeta_N)^{l}}$ となる．$(\zeta_N)^{ln}=1$ であり，$(\zeta_N)^{l} \neq 1$ であるから，この値は $0$ となる．

この 3 つの性質が，後々重要になってきます．

4. 離散フーリエ変換（DFT）

数学的準備を終えたところで，ようやく2節で述べた「作戦」を行います．

以下，$A$ と $B$ の次数の和 $2n$ より大きい最小の 2 べきの数を $N$ とおくこととします（すなわち，正整数 $k$ を用いて $N=2^k$ と表される数）．

4-1. 1 の N 乗根を用いた x の選び方の工夫

2節の最後に提示した作戦では，最初に次のようなことを行うことになっていました．

何かしらの工夫を行って $2n+1$ 個の $x_i$ を選び，それに対応する $A(x_i), B(x_i)$ を求める．

さて，まず最初に考えることとしては，$2n+1$ 個の $x_i$ をどのようにして選ぶかです．

結論から言うと，$N$ 個の $1$ の $N$ 乗根の値を，$x_i$ として選びます（$2n+1$ 個より多く選ぶことになることもありますが，多く選んでしまうぶんには問題ありません）．すなわち，$x_i=(\zeta_N)^{i}$ とするわけです．
なぜこのような選び方をするのか？と思うかもしれませんが，実はこれこそが計算量削減の肝になっていますので，とりあえず今は飲み込んでください．

4-2. 離散フーリエ変換（DFT）

さて，少し脇道にそれます．$N-1$ 次の多項式 $f(x)=c_0 + c_1x + c_2x^2 + \cdots + c_{N-1}x^{N-1}$ を考えます． $x=(\zeta_N)^k$ を代入すると，以下のような $N$ 本の式が立ちます．すなわち

\begin{align}
f((\zeta_N)^0) &= c_0 ((\zeta_N)^{0})^0 + c_1 ((\zeta_N)^{0})^1 + c_2 ((\zeta_N)^{0})^2 + \cdots + c_{N-1} ((\zeta_N)^{0})^{N-1} \\
f((\zeta_N)^1) &= c_0 ((\zeta_N)^{1})^0 + c_1 ((\zeta_N)^{1})^1 + c_2 ((\zeta_N)^{1})^2 + \cdots + c_{N-1} ((\zeta_N)^{1})^{N-1} \\
\vdots \\
f((\zeta_N)^{N-1}) &= c_0 ((\zeta_N)^{N-1})^0 + c_1 ((\zeta_N)^{N-1})^1 + c_2 ((\zeta_N)^{N-1})^2 + \cdots + c_{N-1} ((\zeta_N)^{N-1})^{N-1} \\
\end{align}

のようになるわけです．これらをシグマを用いた式で表すと，

f((\zeta_N)^k)=\sum_{j=0}^{N-1}c_j((\zeta_N)^k)^j
=\sum_{j=0}^{N-1}c_j (\zeta_N)^{jk} (0 \leq k < N）

となります．

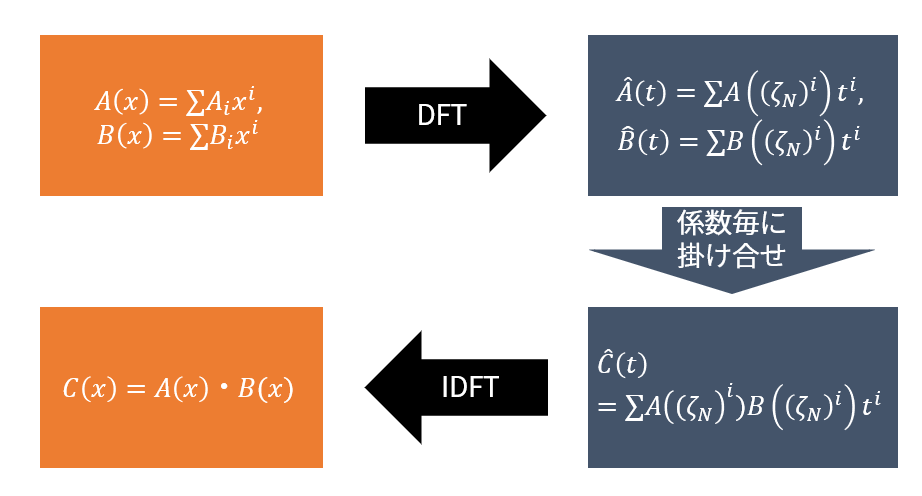
さて，唐突ですが，このようにして求めた $f((\zeta_N)^0), f((\zeta_N)^1), \cdots, f((\zeta_N))^{N-1})$ に対して，これらの値を係数とするような $N-1$ 次の $t$ の多項式 $\hat{f}(t) = \sum_{k=0}^{N-1} f((\zeta_N)^k) t^k$ を考えることにしましょう．この多項式 $\hat{f}(t)$ のことを，$f(x)$ の離散フーリエ変換（Discrete Fourier Transform. 以下「DFT」と略記することがあります）と呼びます．

$\hat{f}(t)$ を，$c_j$ と $t$ で表してみましょう．上記の $\hat{f}(t) = \sum_{k=0}^{N-1} f((\zeta_N)^k) t^k$ に $f((\zeta_N)^k)=\sum_{j=0}^{N-1}c_j((\zeta_N)^k)^j
=\sum_{j=0}^{N-1}c_j (\zeta_N)^{jk}$ を代入することで，

\begin{align}
\hat{f}(t)=\sum_{k=0}^{N-1} \sum_{j=0}^{N-1}c_j (\zeta_N)^{jk}t^k 
\end{align}

と，なることがわかります．

4-3. 離散逆フーリエ変換（IDFT）

さて，またしても唐突ですが，先ほどの $\hat{f}(t)$ に，$t=(\zeta_N)^{-l}(0 \leq l < N)$ を代入した結果がどうなるかを見てみましょう．式が複雑になってきますが，やっていることはあくまでも係数がやたらに長い $t$ の多項式に値を代入しているということなので，その視点を持って読み進めていっていただければと思います．

\begin{align}
\hat{f}((\zeta_N)^{-l})&= \sum_{k=0}^{N-1} \sum_{j=0}^{N-1}c_j (\zeta_N)^{jk}(\zeta_N)^{-jl} \\
&= \sum_{k=0}^{N-1} \sum_{j=0}^{N-1}c_j (\zeta_N)^{k(j-l)}\\

\end{align}

これではややわかりづらいので，足し算の順番を入れ替えてみます．

\begin{align}
\hat{f}((\zeta_N)^{-l})&= \sum_{j=0}^{N-1} c_j(\sum_{k=0}^{N-1}(\zeta_N)^{k(j-l)}) \\
\end{align}

ここで，後ろにある $(\sum_{k=0}^{N-1}(\zeta_N)^{k(j-l)})$ の項に注目してみます．3節で紹介した $1$ の $N$ 乗根の性質を思い返してみましょう．

• $\sum_{k=0}^{N-1}(\zeta_N)^{kl}$ は $l \equiv 0 \pmod N $ のとき $N$，そうでないとき $0$ である．

これにより，$(\sum_{k=0}^{N-1}(\zeta_N)^{k(j-l)})$ は $j = l$ のとき $N$，そうでないとき $0$ になるわけです．この値に $c_j$ を掛け合わせたものを $0 \leq j < N$ の範囲で足し合わせるわけですが，$j =l$ 以外の項は $0$ がかかってしまって残らないので，結局

\begin{align}
\hat{f}(\omega^{-l})&= \sum_{j=0}^{N-1} c_j(\sum_{k=0}^{N-1}(\zeta_N)^{k(j-l)})\\
&= Nc_l\\
\end{align}

となるわけです．よって，

\begin{align}
c_l &= \frac{1}{N}\hat{f}((\zeta_N)^{-l})
\end{align}

となります．これが何を意味するかというと，DFT 後の多項式 $\hat{f}(t)$ から $f(x)$ の係数 $c_i$ が復元できた ということです．これを，離散フーリエ逆変換（Inverse Discrete Fourier Transform. 以下「IDFT」と略記することがあります）と呼びます．

さて，ここまでに出てきた 2 つの処理，DFT と IDFT の関係性について見ていきましょう．ここまでで，次のような処理が行われています．

• DFT では，$c_j$ を係数とする多項式 $f(x)$ に $x=(\zeta_N)^k$ を代入して，そこから得られた $f((\zeta_N)^k)$ を係数とする多項式 $\hat{f}(t)$ を生成している．
• IDFT では，$f((\zeta_N)^k)$ を係数とする多項式 $\hat{f}(t)$ に $x=(\zeta_N)^{-l}$ を代入して，そこから得られた $c_l$ を係数とする多項式 $f(x)$ を生成している．

勘の良い人は気づいたかもしれません．そう，DFT と IDFT は，同じような処理で互いに相反することを行っているのです！　したがって，DFT と IDFT の処理を行うコードは，同じようなものを使えるというわけです．⁵

4-4. DFT と IDFT を用いた多項式補間の方法

さて，ここまでで作戦の詳細を述べるのに必要な概念，DFT と IDFT の説明を行いました．では，話を $A(x)$ と $B(x)$ に戻して，実際に DFT と IDFT を用いて $C(x)$ をどのようにして求めるのかの具体的な作戦がどうなったかをおさらいしましょう．なお，実際には， $A(x)$ や $B(x)$ は $N$ 次より小さい次数の式ではありますが，1節のとき同様に適当に 0 で埋めて $N$ 次にします．

• $N$ 個の $1$ の $N$ 乗根に対して，DFTを用いて $A((\zeta_N)^i), B((\zeta_N)^i)$ の値を求める．
• 求めた $A((\zeta_N)^i), B((\zeta_N)^i)$ に対して，$C((\zeta_N)^i)=A((\zeta_N)^i)B((\zeta_N)^i)$ を求める．
• $C((\zeta_N)^i)$ から，IDFTを用いて $C(x)$ を求める．

2節で述べた作戦の「何かしらの工夫を行って」が，それぞれ「DFTを使って」「IDFTを使って」に変わりました．

しかし，DFT の計算量は愚直に行うと結局 $\Theta(n^2)$ であり，今のままでは結局愚直解から何にも改善されていないことになっています．そのため，計算量改善を行うには，DFT の部分を改善しなければなりません．

果たしてそんなことができる方法があるのでしょうか？

実は，あります．この手法が真に本領発揮するのは，ここからです．

5. 高速フーリエ変換

5-1. 高速フーリエ変換の手法

さて，DFT をより高速に行う方法を説明します．（IDFT は DFT と同じような処理なので省略します）

4.2 節のように $N-1$ 次の多項式 $f(x)=c_0 + c_1x + c_2x^2 + \cdots + c_{N-1}x^{N-1}$ を考えます．

この多項式 $f(x)$ に対して，偶数次の項のみを順番に並べた $N/2 - 1$ 次の多項式 $f_e(x)$ と，奇数次の項のみを順番に並べた $N/2 - 1$ 次の多項式 $f_o(x)$ を考えることにしてみましょう．すなわち

\begin{align}
f_e(x) &= c_0 + c_2x + \cdots + c_{N - 2}x^{N/2 - 1} \\
f_o(x) &= c_1 + c_3x + \cdots + c_{N - 1}x^{N/2 - 1}
\end{align}

のような $f_e(x), f_o(x)$ を考えます．すると，$f(x)=f_e(x^2) + xf_o(x^2)$ と表せます．

さて，4-2節で，$x = (\zeta_N)^k(0 \leq k < N)$ を代入した $N$ 個の値を用いることによって DFT ができることがわかりました．これにしたがって， $f(x)=f_e(x^2) + xf_o(x^2)$ に $x = (\zeta_N)^k(0 \leq k < N)$ を代入したとき，$f_e(x)$ と $f_o(x)$ に関してどのような値の情報が必要かを見てみることにすると，

• $f_e((\zeta_N)^0), f_e((\zeta_N)^2), \cdots, f_e((\zeta_N)^{2N-2})$ の値の情報が必要である．
• $f_o((\zeta_N)^0), f_o((\zeta_N)^2), \cdots, f_o((\zeta_N)^{2N-2})$ の値の情報が必要である．

ここで，$(\zeta_N)^2 = \zeta_{N/2}$ が成り立つことに注意して（$\zeta_N = e^{iπ/N}, \zeta_{N/2} = e^{iπ/(N/2)}$であることからわかります）上記を言い換えると，

• $f_e((\zeta_{N/2})^0), f_e((\zeta_{N/2})^1), \cdots, f_e((\zeta_{N/2})^{N/2-1}), f_e((\zeta_{N/2})^{N/2}), \cdots, f_e((\zeta_{N/2})^{N - 1})$ の値の情報が必要である．
• $f_o((\zeta_{N/2})^0), f_o((\zeta_{N/2})^1), \cdots, f_o((\zeta_{N/2})^{N/2-1}), f_o((\zeta_{N/2})^{N/2}), \cdots, f_o((\zeta_{N/2})^{N - 1})$ の値の情報が必要である．

さて，3節で述べた $1$ の $N$ 乗根の性質を用いると，$(\zeta_{N/2})^{N/2}=1$ です．したがって，上記の $f_e, f_o$ について，それぞれ前半と後半は同じものを指します．したがって，結局上記は次のように言い換えられます．

• $f_e((\zeta_{N/2})^0), f_e((\zeta_{N/2})^1), \cdots, f_e((\zeta_{N/2})^{N/2-1})$ の値の情報が必要である．
• $f_o((\zeta_{N/2})^0), f_o((\zeta_{N/2})^1), \cdots, f_o((\zeta_{N/2})^{N/2-1})$ の値の情報が必要である．

このことは，$f_e(x)$ と $f_o(x)$ のそれぞれに対して，$N/2$ 個の値の情報が必要であることを意味します．これは $f(x)$ に必要な情報の数の半分です．したがって，DFT は，次数が半分の多項式の DFT 2回によって求められるということがわかります．

結局，$N-1$ 次多項式 $f(x)$ の DFT は次のように計算すればよい，ということになります．

• $N=1$ のとき，$f(x)=c_0$ のように定数関数となるので，DFT はもはや計算するまでもなく，$
  c_0$ である．
• $N \geq 2$ のとき，$f(x) = f_e(x^2) + xf_o(x^2)$ とおけ，$f_e(x)$ と $f_o(x)$ の DFT がそれぞれ計算済みであるとするならば，その結果を使って $f(x)$ の DFT がマージできる．具体的には，$f((\zeta_N)^k)$ を求めたいというとき，これは $f((\zeta_N)^k) = f_e((\zeta_{N/2})^k) + ((\zeta_N)^k) f_o((\zeta_{N/2})^k)$ のように計算でき，これを全ての $0 \leq k < N$ に対して行えばよい．

このようにして，より次数の小さい関数の DFT の結果を使って大きい関数の DFT を計算していく手法を，高速フーリエ変換（FFT）と呼びます．

5-2. 高速フーリエ変換の計算量解析

さて，FFT の計算量がどのようになるか見ていきましょう．

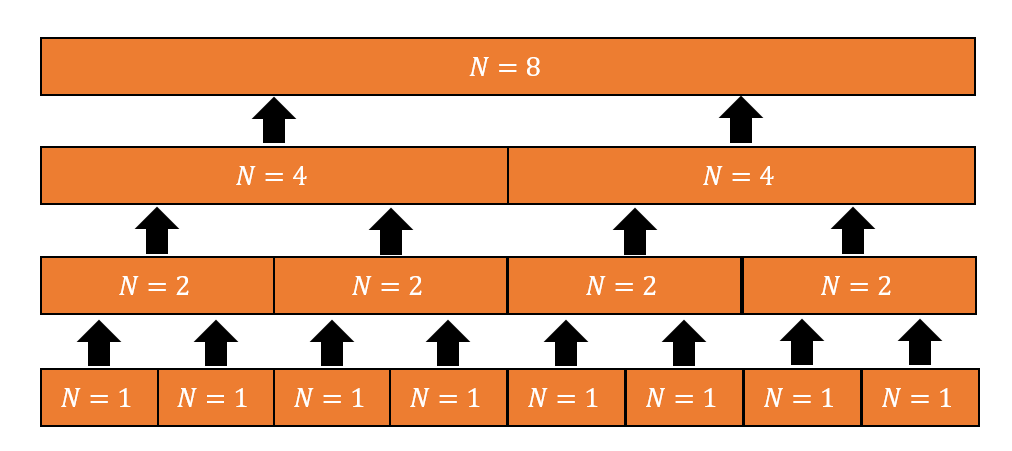
マージの流れを図に表すと，以下の図のようになります．

5-1節で述べた通り，2 つの DFT の結果のマージは多項式の次数に対して線形の計算回数で行えました．したがって，計算回数は，マージの様子を上の図のように表したとき，その帯の長さの総和に等しいことがわかります．

上の図で，帯は全部で $(\log_{2}N + 1)$ 本あります．それぞれの帯で，長さは $N$ で全て等しいです．したがって，帯の長さの総和は $N \times (\log_{2}N+1)$ です．⁶

結局，FFT の計算量は，$O(n \log n)$ であることがわかりました．愚直解の計算量が $O(n^2)$ だったため，確かに計算量が落とせていることがわかります！

6. 高速フーリエ変換の実装

では，高速フーリエ変換をどのように実装すればよいかを見ていきましょう．

「小さい計算結果を利用して，大きい計算結果を計算する」という構造となっているため，以下のように，再帰で実装するのが楽でしょう．

#include <iostream>
#include <vector>
#include <complex>
using namespace std;

// π の値を計算しておく．
double pi = acos(-1);

vector<complex<double>> fft(vector<complex<double>> &a, double inv){
    // inv = 1 ならば普通の FFT，inv = -1 ならば IFFT になるようにする．
    int n = a.size();
    vector<complex<double>> ret(0);
    // a のサイズが 1 であるときは，それがそのまま DFT である．
    if (n == 1){
        return a;
    }
    else{
        vector<complex<double>> even(0);
        vector<complex<double>> odd(0);
        for (int i = 0; i < n; i++){
            if (i % 2 == 0) even.push_back(a[i]);
            else odd.push_back(a[i]);
        }
        // even と odd の DFT を，再帰的に求める．
        vector<complex<double>> d_even = fft(even, inv);
        vector<complex<double>> d_odd = fft(odd, inv);

        double dn = (double)n;

        // zeta を求める．IFFT のときは，偏角を -1 倍する．
        complex<double> zeta(cos(2 * pi * inv / dn), sin(2 * pi * inv / dn));
        
        complex<double> now = 1;
        for (int i = 0; i < n; i++){
            ret.push_back(d_even[i % (n / 2)] + now * d_odd[i % (n / 2)]);
            now *= zeta;
        }
    }
    return ret;
}


vector<double> convolution(vector<complex<double>> &a, vector<complex<double>> &b){
    // 配列 a, b は，それぞれ A(x) と B(x) の係数を次数の小さい順に並べたもの．
    int len_a = a.size();
    int len_b = b.size();
    int len_c = len_a + len_b - 1; // len_c は A(x) * B(x) の次数
    int n = 1;
    // len_c より大きい最小の 2 べきの数を求める
    while(n <= len_c){
        n *= 2;
    }

    // 配列の長さが n になるまで，配列の末尾に 0 を追加する
    while(a.size() < n){
        a.push_back(0.0);
    }
    while(b.size() < n){
        b.push_back(0.0);
    }

    // A(x) の FFT DA(t), b(x) の FFT DB(t) を求める．
    // 配列 da, db は，それぞれ DA(t), DB(t) の係数を次数の小さい順に並べたもの．
    vector<complex<double>> da = fft(a, 1);
    vector<complex<double>> db = fft(b, 1);

    // C(x) の FFT DC(t). これの k 次の係数は， DA(t) と DB(t) の k 次の係数を掛け合わせれば求まる．
    vector<complex<double>> dc(n);
    for (int i = 0; i < n; i++){
        dc[i] = da[i] * db[i];
    }

    // C(x) は DC(t) を IFFT すれば求まる．このようにしてできた配列 c は，C(x) の係数を次数の小さい順に並べたものとなっている．
    vector<complex<double>> c = fft(dc, -1);

    // IFFT の後は最後に n で割ることを忘れずに．
    vector<double> ret(0);
    for (int i = 0; i < n; i++){
        double dn = (double)n;
        ret.push_back(c[i].real() / dn);
    }
    return ret;
}

int main(){
    int na;
    int nb;
    cin >> na >> nb;
    // a は A(x) の係数を次数の小さい順に並べたもの． b は B(x) の係数を次数の小さい順に並べたもの．
    vector<complex<double>> a(na);
    vector<complex<double>> b(nb);
    
    // 入力を受け取る．
    for (int i = 0; i < na; i++){
        cin >> a[i];
    }
    for (int i = 0; i < nb; i++){
        cin >> b[i];
    }

    // convolution 関数で A(x) と B(x) の多項式乗算を行い，C(x) = A(x) * B(x) の係数を小さい順に並べた配列 c を返す．
    vector<double> c = convolution(a, b);
    for (int i = 0; i < na + nb - 1; i++){
        cout << round(c[i]) << endl;
    }
}

実際に，この関数を使って， $A(x) = 1 + 2x + 3x^2, B(x) = 2 + 3x + 4x^2$ として，$C(x)=A(x)B(x)$ が正しく求められているか，確かめてみましょう．実際に計算してみたらわかりますが，$C(x)=2 + 7x + 16x^2 + 17x^3 + 12x^4$ となります．

入力

3 3
1 2 3
2 3 4

出力

2
7
16
17
12

確かに正しい結果が返ってきました！これで，多項式乗算を高速に行うことができました．

7. 高速フーリエ変換の欠点と，その解決策

さて，このようにして高速に多項式乗算を行える高速フーリエ変換ですが，一つ致命的な弱点があります．

試しに，$A(x)=1 + 10^9x, B(x)=2+10^9x$ として，$C(x)=A(x)B(x)$ を求めてみましょう．実際に計算してみたらわかりますが，$C(x)=10^{18}x + 3 \times 10^9x + 2$ となります．

入力

2 2
1 1000000000
2 1000000000

出力

0
2999999969
1000000000000000000

！？値がずれている？？？

そう，FFT の計算には $1$ の $N$ 乗根の計算に小数を用いている以上，値が大きくなるとどうしても誤差が発生してしまう，という欠点があります．⁷

競技プログラミングでは，FFT を用いる計算で用いる値が非常に大きくなることがあり，こうなると全く手に負えません．（そのように，値が非常に大きくなるような場合には，たいてい「答えをある値で割った余りを出力する」というような要求がなされますが）

これを解決する方法としては，FFT と同じことを整数の範囲内で行うということが考えられます．しかし，そんなことが本当にできる方法はあるのでしょうか？

実は，あります．詳しいことは次の節で述べます．

8. 高速フーリエ変換を整数の範囲内で行う工夫　～そして数論変換へ～

8-1. FFT を行える条件

これまでの FFT には，$1$ の $N$ 乗根を用いました．これは，$1$ の $N$ 乗根が，3節にあるような 3 つの性質を満たしており，それが FFT を行う上で都合が良かったからです．

• $(\zeta_N)^{N}=1$
• $(\zeta_N)^{0}, (\zeta_N)^{1}, (\zeta_N)^{2}, \cdots, (\zeta_N)^{N-1}$ はすべて異なる．
• $\sum_{k=0}^{N-1}(\zeta_N)^{kl}$ は $l \equiv 0 \pmod N $ のとき $N$，そうでないとき $0$ である．

したがって，このような $\zeta_N$ と同じ性質を持つ「代わりになる何か」が整数の範囲内で計算できるものの中に存在すれば，それを使って「FFT と同じようなこと」が実現できるわけです．

果たしてそんなに都合の良い「代わりとなる何か」が整数の範囲内で存在するのでしょうか？

実は存在します．次の節でそれが何か取り上げることにしましょう．

8-2. mod p の値で 1 の N 乗根と同じような状況を作り出す

さて，唐突ですが，$p$ を適当な素数として，$\bmod p$ での計算体系を考えてみることにしてみます．この計算体系の中に，$\zeta_N$ と同じ働きをするものがあればよいわけです．（$p$ にどのような素数を用いるのがよいかは後述します）

実は，このような働きをするような数が存在します．ここで重要となるのが，$\bmod p$ における原子根という値の存在です．

原始根の説明の前に，次に示すフェルマーの小定理について触れておきましょう．この定理は，この記事でここから先よく登場します．

$p$ が素数で，$r$ が $p$ と互いに素であるとき，$r^{p-1} \equiv 1 \pmod p$ である．

これを踏まえた上で，原始根の説明に戻ります．原始根とは，次のような条件を満たす正整数 $r$ のことを指します．

$r^x \equiv 1 \pmod p$ となるような最小の正整数 $x$ が $p-1$ となるような $r$ を，$p$ の原始根という．

フェルマーの小定理より，$p$ の倍数でない $r$ は $p-1$ 乗したら必ず $1$ になります．原始根とは，そこまでに $1$ にはなることはない，ということを言っているわけです．

ここで気になるのが，そんな都合の良い数なんて本当に存在するのか，ということでしょう．実はこのような数は必ず存在することが示せます（原始根の存在定理）．証明は難しいので，この記事では省略します．⁸

さて，話を戻します．先程まで見てきたことを踏まえると，mod の世界では，$1$ の $N$ 乗根にあったような周期性がありそうです． $1$ の $N$ 乗根の代わりに $\bmod p$ での計算体系が使えるのではないか，と考えられます．ここで，$\bmod p$ において，とある $r_N$ が存在し（ここでの $r_N$ は $p$ の原始根とは限らないことに注意してください），それが次の 3 つの条件を満たせば，$1$ の $N$ 乗根の代わりになりそうです．

• $(r_N)^{N} \equiv 1 \pmod p$
• $(r_N)^0, (r_N)^1, \cdots, (r_N)^{N-1}$ は $\bmod p$ においてすべて異なる．
• $\sum_{k=0}^{N-1}(r_N)^{kl}$ は $l \equiv 0 \pmod{N}$ のときに $N$，そうでないとき $0$ である．

このような $r_N$ が都合よく存在するのかも含めて，次の節でより詳しく述べていきます．

9. 数論変換

9-1. 数論変換の手法

8節で見たような，FFT において $1$ の $N$ 乗根の代わりに $\bmod p$ 上での計算を用いたものを，数論変換（NTT）と言います．

FFT と NTT とで異なる箇所は，主に $\zeta_N$ が $r$ に変わっていることでした．このことを考えると，FFT で行われる次のような処理は，例えば NTT では次のように実現できます．

• $\zeta_N$ をかける → $\bmod p$ 上で $r$ をかける．
• $(\zeta_N)^{-1}$ をかける → $\bmod p$ 上での $r$ の逆元⁹をかける．

FFT に比べて，NTT のメリットは，何と言っても「小数誤差が発生しない」ということでしょう．小数誤差を考えずに整数の範囲内だけで FFT と同じことができるというだけあって，非常にありがたいです．一方で，デメリットもあります．全ての計算を $\bmod p$ の計算体系を用いて行っているというわけで，最終的に得られる値は $\bmod p$ の値に限られてしまうということには注意しなければなりません．

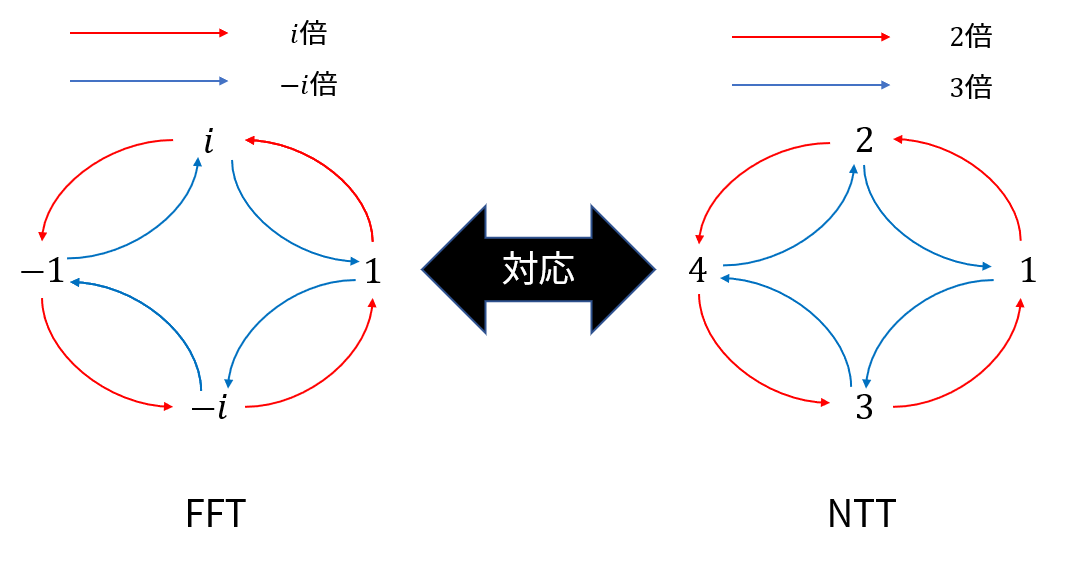
試しにひとつ例を挙げます．$N=4$ のときについて考えてみましょう．今までの FFT では，$1$ の $4$ 乗根 $\zeta_4 = i$ が用いられていました．しかし，NTT では $\bmod p$ の計算体系を使います．ここでは，$p=5$ とし，$r$ には $r=2$ を採用することにしましょう．そうすると，$r^2 \equiv 4, r^3 \equiv 3, r^4 \equiv 1$ であるので，$r$ は 8 節の最後で述べた条件を満たすことがわかります．よって，FFT での「$i$ をかける」と，NTT での「$2$ をかける」が，対応していることがわかります．また，FFT での「$-i$ をかける」は，NTT では $\bmod 5$ における $2$ の逆元が $3$ であることを利用すると，「$3$ をかける」に対応する，ということもわかります．

9-2. 数論変換で用いられる p の値は？

さて，あと考えるべきことは，$(r_N)^N \equiv 1 \pmod p$ を満たすようにするにはどのようにするかということですが，8節で述べたフェルマーの小定理より，$p$ と互いに素であるような $r$ に対して，$r^{p-1} \equiv 1 \pmod p$ となります．したがって，$r$ を $p$ の原始根としたとき，$r_N = r^{(p-1)/N}$ とすれば，次に示す条件を全て満たせることがわかります．

• $(r_N)^{N} \equiv 1 \pmod p$
• $(r_N)^0, (r_N)^1, \cdots, (r_N)^{N-1}$ は $\bmod p$ においてすべて異なる．
• $\sum_{k=0}^{N-1}(r_N)^{kl}$ は $l \equiv 0 \pmod{N}$ のときに $N$，そうでないとき $0$ である．

真ん中の性質の証明：仮に $(r_N)^j = (r_N)^k$ なる $j,k$ が $0 \leq j < k \leq N-1$ に存在したとする．このとき，$(r_N)^{k-j} \equiv 1 \pmod p$ である．これは，$r^{(k-j)(p-1)/N} \equiv 1$ のように変形でき，$r$ が原子根であることに矛盾する．したがって，そのような $j,k$ は存在せず，ゆえに $(r_N)^0, (r_N)^1, \cdots, (r_N)^{N-1}$ は $\bmod p$ においてすべて異なる．
一番下の性質の証明：等比級数の和の公式を，$1$ の $N$ 乗根のときと同じように適用すればよい．

......ただしこれができるのは， $p-1$ が $N$ で割り切れる場合に限ります．（割り切れない場合，$r^i = r_N$ となるような整数 $i$ が存在せず，$r_N$ が存在しなくなってしまう）¹⁰

FFT では，半分のサイズの問題を繰り返し解く，ということを実現するべく，$N$ を 2 べきの値に設定したのでした．NTT でもこれは変わらず，$N$ を 2 べきの値に設定する必要があるわけですが，$p$ の値によって，許される $N$ が大きく変わってしまう，ということを意味します．
例えば，$p=17$ に設定した場合，$p-1=16$ となるため，$p-1$ を割り切る 2 べきの $N$ の最大値 $N=16=2^4$ までは計算できるわけですが，$p=19$ と設定してしまうと，$p-1=18$ となり，$p-1$ を割り切る 2 べきの $N$ の最大値は $2$ となってしまいます．

よって $p$ は，$p-1$ ができるだけ大きな 2 べきの値を割り切るように取るのがよい，ということがわかります．

9-3. 競プロで 998244353 がよく使われる理由

9-2節では，NTT を行うために満たすべき $p$ の条件について述べたわけですが，ではそのような素数 $p$ にはどのようなものがあるのでしょうか？

結論から言うと， $p=998244353$ がかなり都合の良い数です．というのも，$998244353 = 119 \times 2^{23} + 1$ であり，$p-1$ は $N=2^{23}$ までの 2 べきの数で割り切れるため，$N=2^{23}(=8388608)$ まで許されます．ここまでのサイズが許されるのであれば，競技プログラミングでの現実的な実行時間内で出てくる制約には十分すぎるでしょう¹¹．

そのこともあってか，競技プログラミングで NTT が想定解の問題が出題された場合，答えで mod を取らせるような問題での mod の値は $998244353$ がしばしば用いられます．

一方で，主に昔の競技プログラミングの問題では mod としてしばしば $10^9+7$¹² が用いられていました．$p=10^9+7$ はどうなのでしょうか？結論から言うと，$10^9 + 7 = 500000003 \times 2 + 1$ であり，なんと $N=2$ までしか許されません．流石にこれは実用的ではなく，NTT と非常に相性の悪い mod となってしまった，というわけです．

なお，「mod の値が $998244353$ だと解法は NTT だろう」というメタ読みを防止する目的からか，最近の AtCoder Beginner Contest では，mod の値はたいていは $998244353$ に統一されています．¹³

10. 数論変換の実装

ここでは，mod として $998244353$ を用います．（競技プログラミングでは，多くの場合それで事足ります）

$998244353$ の原始根のひとつは $3$ であることが知られているため，$r=3$ を用いればよいです．

実装については，FFT とほとんど変わりません．FFT で $\zeta_N$ を用いていたところを，NTT では $r_N$ に置き換えればよいです．

ただし，実装上の注意として，$(r_N)^i$ をいちいち繰り返し二乗法で $O(\log i)$ で計算していては，計算量が悪くなります．そのため，$(r_N)^i$ で必要となる値（およびその逆元も）は，あらかじめ前計算しておくことにしましょう．

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

long long p = 998244353; // NTT に相性の良い mod は 998244353．

// 繰り返し二乗法で x ^ n を mod で割った余りを求める．
long long my_pow(long long x, long long n, long long mod){
    long long ret;
    if (n == 0){
        ret = 1;
    }
    else if (n % 2 == 1){
        ret = (x * my_pow((x * x) % mod, n / 2, mod)) % mod;
    }
    else{
        ret = my_pow((x * x) % mod, n / 2, mod);
    }
    return ret;
}

// mod を法とする x の逆元を計算する．
long long mod_inv(long long x, long long mod){
    return my_pow(x, mod - 2, mod);
}

vector<long long> ntt(vector<long long> &a, long long depth, vector<long long> &root){
    // inv = 1 ならば普通の NTT，inv = -1 ならば INTT になるようにする（今回は，呼び出す root が逆元かそうでないかによって調整する）．
    long long n = a.size();
    vector<long long> ret(0);
    // a のサイズが 1 であるときは，それがそのまま DFT である．
    if (n == 1){
        return a;
    }
    else{
        vector<long long> even(0);
        vector<long long> odd(0);
        for (long long i = 0; i < n; i++){
            if (i % 2 == 0) even.push_back(a[i]);
            else odd.push_back(a[i]);
        }
        // even と odd の DFT を，再帰的に求める．
        vector<long long> d_even = ntt(even, depth - 1, root);
        vector<long long> d_odd = ntt(odd, depth - 1, root);

        long long r = root[depth];
        
        long long now = 1;
        for (long long i = 0; i < n; i++){
            ret.push_back((d_even[i % (n / 2)] + (now * d_odd[i % (n / 2)]) % p) % p);
            now = (now * r) % p;
        }
    }
    return ret;
}


vector<long long> convolution(vector<long long> &a, vector<long long> &b, vector<long long> &root, vector<long long> &invroot){
    // 配列 a, b は，それぞれ A(x) と B(x) の係数を次数の小さい順に並べたもの．
    int len_a = a.size();
    int len_b = b.size();
    int len_c = len_a + len_b - 1; // len_c は A(x) * B(x) の次数
    int n = 1;
    // len_c より大きい最小の 2 べきの数を求める
    while(n <= len_c){
        n *= 2;
    }

    // 配列の長さが n になるまで，配列の末尾に 0 を追加する
    while(a.size() < n){
        a.push_back(0LL);
    }
    while(b.size() < n){
        b.push_back(0LL);
    }


    long long log_2n = 1;
    while ((1LL << log_2n) < n){
        log_2n++;
    }

    // A(x) の NTT DA(t), b(x) の NTT DB(t) を求める．
    // 配列 da, db は，それぞれ DA(t), DB(t) の係数を次数の小さい順に並べたもの．
    vector<long long> da = ntt(a, log_2n - 1, root);
    vector<long long> db = ntt(b, log_2n - 1, root);

    // C(x) の NTT DC(t). これの k 次の係数は， DA(t) と DB(t) の k 次の係数を掛け合わせれば求まる．
    vector<long long> dc(n);
    for (int i = 0; i < n; i++){
        dc[i] = (da[i] * db[i]) % p;
    }

    // C(x) は DC(t) を INTT すれば求まる．このようにしてできた配列 c は，C(x) の係数を次数の小さい順に並べたものとなっている．
    vector<long long> c = ntt(dc, log_2n - 1, invroot);

    // INTT の後は最後に n で割ることを忘れずに．
    vector<long long> ret(0);
    for (int i = 0; i < n; i++){
        ret.push_back((c[i] * mod_inv((long long)n, p)) % p);
    }
    return ret;
}

// NTT に必要となる r の累乗数を求める．
vector<long long> make_root(long long mod){
    vector<long long> ret(0);
    long long r = my_pow(3, 119, mod);
    for (long long i = 0; i < 23; i++){
        ret.push_back(r);
        r = (r * r) % mod;
    }
    reverse(ret.begin(), ret.end());
    return ret;
}

// NTT に必要となる r の累乗数の逆元を求める．
vector<long long> make_invroot(vector<long long> &root, long long mod){
    vector<long long> ret;
    for (long long i = 0; i < root.size(); i++){
        ret.push_back(mod_inv(root[i], mod));
    }
    return ret;
}

int main(){
    int na;
    int nb;
    cin >> na >> nb;
    // a は A(x) の係数を次数の小さい順に並べたもの． b は B(x) の係数を次数の小さい順に並べたもの．
    vector<long long> a(na);
    vector<long long> b(nb);
    
    // 入力を受け取る．
    for (int i = 0; i < na; i++){
        cin >> a[i];
    }
    for (int i = 0; i < nb; i++){
        cin >> b[i];
    }

    // NTT で必要となる r の累乗数を前計算しておく（これをしないと計算量が悪くなる）．
    vector<long long> root = make_root(p);
    vector<long long> invroot = make_invroot(root, p);

    // convolution 関数で A(x) と B(x) の多項式乗算を行い，C(x) = A(x) * B(x) の係数を小さい順に並べた配列 c を返す．
    vector<long long> c = convolution(a, b, root, invroot);
    for (int i = 0; i < na + nb - 1; i++){
        cout << c[i] << endl;
    }
}

実際に，この関数を使って， $A(x) = 1 + 2x + 3x^2, B(x) = 2 + 3x + 4x^2$ として，$C(x)=A(x)B(x)$ が正しく求められているか，確かめてみましょう．実際に計算してみたらわかりますが，$C(x)=2 + 7x + 16x^2 + 17x^3 + 12x^4$ となります．

入力

3 3
1 2 3
2 3 4

出力

2
7
16
17
12

確かに正しい結果が返ってきました！

11. 高速フーリエ変換・数論変換を用いて解ける問題

ここからは，今までに触れてきた高速フーリエ変換・数論変換を用いて解ける問題を，いくつか例を挙げて見ていきます．

11-1. AtCoder Typical Contest 001 C問題「高速フーリエ変換」

典型問題の練習用と位置付けられたコンテストで，まさに FFT の練習用とも言うべき問題です．
6節の実装例にあるコードを少し改変すれば AC が得られます．

11-2. AtCoder Library Practice Contest F問題「Convolution」

こちらはライブラリの確認用と位置付けられたコンテストで，NTT の練習問題とも言うべき問題です．
10節の実装例にあるコードを少し改変すれば AC が得られます．

11-3. 競プロ典型 90 問¹⁴ 065「RGB Balls 2」

NTT はこのような数え上げの問題にもしばしば用いられます．

問題文を言い換えると，赤色のボールを $K-Y$ 個以上，緑色のボールを $K-Z$ 個以上，青色のボールを $K-X$ 個以上選び，$K$ 個のボールを選ぶやり方が何通りあるか，という問題に言い換えられます．

ここで，赤色のボールを $r$ 個選ぶとすると，緑色のボールと青色のボールを合わせて $K-r$　個選ぶことになります．よって，答えは $\sum_{K-Y \leq r \leq K}\binom{R}{r}(\sum_{g + b = K - r, K - Z \leq g \leq G, K - X \leq b \leq B}\binom{G}{g}\binom{B}{b})$ となります．この，$(\sum_{g + b = K - X, K - Z \leq g \leq G, K - X \leq b \leq B}\binom{G}{g}\binom{B}{b})$ を全ての $r$ に対して計算することが，NTT を用いることで $O(K \log K)$ で出来るので，この問題を $O(K \log K)$ で解くことができます．実装例は以下の通りです．

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

long long p = 998244353;
long long MAX_VAL = 200000;

int main(){
    long long R,G,B,K;
    cin >> R >> G >> B >> K;
    long long X,Y,Z;
    cin >> X >> Y >> Z;

    // 階乗の前計算．
    vector<long long> fact(MAX_VAL + 1, 0);
    fact[0] = 1;
    for (long long i = 0; i < MAX_VAL; i++){
        fact[i + 1] = (fact[i] * (i + 1)) % p;
    }

    // 階乗の逆元の前計算．
    vector<long long> invfact(MAX_VAL + 1, 0);
    for (long long i = 0; i <= MAX_VAL; i++){
        invfact[i] = mod_inv(fact[i], p);
    }

    // 赤を選ぶ通り数を記録
    vector<long long> red(K + 1, 0);
    for (long long i = max(0LL, K - Y); i <= K; i++){
        if (i > R) continue;
        red[i] = (fact[R] * ((invfact[i] * invfact[R - i]) % p)) % p;
    }
    // 緑を選ぶ通り数を記録
    vector<long long> green(K + 1, 0);
    for (long long i = max(0LL, K - Z); i <= K; i++){
        if (i > G) continue;
        green[i] = (fact[G] * ((invfact[i] * invfact[G - i]) % p)) % p;
    }
    // 青を選ぶ通り数を記録
    vector<long long> blue(K + 1, 0);
    for (long long i = max(0LL, K - X); i <= K; i++){
        if (i > B) continue;
        blue[i] = (fact[B] * ((invfact[i] * invfact[B - i]) % p)) % p;
    }

    vector<long long> root = make_root(p);
    vector<long long> invroot = make_invroot(root, p);

    // 緑と青での選ぶ通り数を多項式とみなして掛け合わせ
    vector<long long> green_blue_conv = convolution(green, blue, root, invroot);

    long long ans = 0;
    for (long long i = K - Y; i <= K; i++){
        ans = (ans + (red[i] * green_blue_conv[K - i])) % p;
    }
    cout << ans << endl;
}

11-4. ABC196-F「Substring 2」

$S$ の部分文字列の中で $T$ と合わせるのに最適な箇所が見つかるなどは考えづらいので，全ての部分文字列に対して何文字置き換えるかを求めるほかなさそうです．「何文字置き換えなければならないか」＝ $T$ の文字数－「何文字一致しているか」なので，以降は「何文字一致しているか」を求めることを考えましょう．

さて，$S$ の，長さ $|T|$ の部分文字列と，$T$ に対して，「何文字一致しているか」は，「両方とも 1 であるような箇所の数」＋「両方とも 0 であるような箇所の数」のように分解できます．

以下では，まず，「両方とも 1 であるような箇所の数」を求めることを考えましょう．

ここで，$s,t$ を，それぞれ $S,T$ を数の配列とみなしたものと考えます．そうすると，$s$ の $i$ 番目から始まる長さ $|t|$ の部分列と，$t$ に対して，「両方とも 1 であるような箇所の数」は，$\sum_{j=1}^{|t|}s_{i+j}t_j$ と求まります．

この式のままではいまいち見通しが悪いので，$t$ を前後反転させます．すると，$\sum_{j=1}^{|t|}s_{i+j}t_{|t|+1-j}$ となります．これだと FFT・NTT で計算可能な形になっていそうです．これを FFT や NTT で計算することで，「両方とも 1 であるような箇所の数」が全ての部分列に対して求まりました．

あとは，「両方とも 0 であるような箇所の数」ですが，これは全てのビットを反転させて同じことをやれば求まります．よって「何文字一致しているか」が全ての部分列に対して求まったので，この問題が解けました．

ただし，この問題では制約が大きいため，定数倍高速化が要求されます¹⁵．AtCoder Library は超高速なので，ぜひ活用しましょう．実装は以下の通りです（AtCoder Libraryを用いています）．

#include <iostream>
#include <vector>
#include <string>
#include <atcoder/convolution>
using namespace std;
using namespace atcoder;

int main(){
    string S;
    string T;
    cin >> S >> T;
    reverse(T.begin(), T.end());

    // s, t は，S, T 内の各文字をそのまま数字に直した配列．
    // s_rev, t_rev は，S, T 内の各文字をビット反転して数字に直した配列．
    vector<long long> s(S.size());
    vector<long long> t(T.size());
    vector<long long> s_rev(S.size());
    vector<long long> t_rev(T.size());

    for (int i = 0; i < S.size(); i++){
        if (S[i] == '0'){
            s[i] = 0;
            s_rev[i] = 1;
        }
        else{
            s[i] = 1;
            s_rev[i] = 0;
        }
    }
    for (int i = 0; i < T.size(); i++){
        if (T[i] == '0'){
            t[i] = 0;
            t_rev[i] = 1;
        }
        else{
            t[i] = 1;
            t_rev[i] = 0;
        }
    }

    // そのままの数列，およびビット反転した数列のそれぞれに対して，NTT を行う．
    vector<long long> conv = convolution<998244353>(s, t);
    vector<long long> conv_rev = convolution<998244353>(s_rev, t_rev);

    long long ans = T.size();

    // T の文字数から「両方 0 の文字数」「両方 1 の文字数」を引いたものが，書き換える必要のある文字数．
    for (int i = T.size() - 1; i <= conv.size() - T.size(); i++){
        ans = min(ans, (long long)T.size() - conv[i] - conv_rev[i]);
    }
    cout << ans << endl;
}

11-5. ABC267-Ex「Odd Sum」

動的計画法（DP）を使って解くようなタイプの問題ですが，このような DP の高速化にも，NTT がしばしば用いられます．

本問の場合，まず，初めに DP テーブルの組み方からして工夫する必要があります．$dp[i][j]=(i 番目まで見て，総和が j)$ と組みたくなってしまうところですが，今回はそうせず，次のように組みます（種類数が少ないことに注目すると，こちらの組み方のほうが状態数を減らせるのです）．

• $dp0[i][j]=(i 種類目の数字まで見て，総和が j で，偶数個を選んだときの選び方の個数)$
• $dp1[i][j]=(i 種類目の数字まで見て，総和が j で，奇数個を選んだときの選び方の個数)$

このようにして，同じ種類の数字の選び方は一気に決めます．（同じ種類の数字の選び方は二項係数を使えば求められます）

具体的には，まず，$i$ 番目に見た数字が $x$ であるとき，$x$ を偶数個選んで総和を $k$ にする方法の数を $tmp0(x, k)$，奇数個選んで総和を $k$ にする方法の数を $tmp1(x, k)$ としましょう．すると，$A$ の中に $x$ がある個数を $C(x)$ として，

tmp0(x, k) = \left\{
\begin{array}{ll}
\binom{C(x)}{k / x} & (k が 2x の倍数のとき) \\
0 & (それ以外)
\end{array}
\right.
\\
tmp1(x, k) = \left\{
\begin{array}{ll}
\binom{C(x)}{k / x} & (k が x の倍数だが，2x の倍数ではないとき) \\
0 & (それ以外)
\end{array}
\right.

と求められます．そうすれば，この $tmp0(x, k), tmp1(x, k)$ を用いることで，$i$ 番目に見た数字の種類が $x$ であるとき，

• $dp0[i+1][j] = \sum dp0[i][j-k] \times tmp0(x,k) + \sum dp1[i][j-k] \times tmp1(x,k)$
• $dp1[i+1][j] = \sum dp0[i][j-k] \times tmp1(x,k) + \sum dp1[i][j-k] \times tmp0(x,k)$

のように遷移できます．$A_{max} = 10$ とし，これを愚直に遷移すると $O(N + A_{max} M^2)$ かかってしまうので実行時間制限に間に合いませんが，よく見ると遷移が NTT で計算可能な式の形となっているため，遷移を NTT で高速化させることによって計算量を $O(N + A_{max} M \log M)$ に落とすことができます．

しかし，この問題は，実行時間制限が前問以上に厳しいです¹⁶．そのため，AtCoder Library などの高速な NTT ライブラリを用いるほかに，定数倍高速化の工夫も要求されます．

例えば，次のような工夫を行います．

• ある時点の計算で必要なぶんだけの配列を確保し，必要ない部分まで NTT を行って余計に時間を食うようなことのないようにする．
• その上で，見る数字の種類の順番を，登場頻度の低い順にすることで，早い段階から多くの領域が必要になってしまうことを防ぐ．

このような工夫を行うことで，ようやく実行時間制限に間に合い，正解することができます．実装例は以下の通りです（AtCoder Library を用いています）．

#include <iostream>
#include <vector>
#include <atcoder/convolution>
using namespace std;
using namespace atcoder;

long long p = 998244353;

// 繰り返し二乗法で x ^ n を mod で割った余りを求める．
long long my_pow(long long x, long long n, long long mod){
    long long ret;
    if (n == 0){
        ret = 1;
    }
    else if (n % 2 == 1){
        ret = (x * my_pow((x * x) % mod, n / 2, mod)) % mod;
    }
    else{
        ret = my_pow((x * x) % mod, n / 2, mod);
    }
    return ret;
}

// mod を法とする x の逆元を計算する．
long long mod_inv(long long x, long long mod){
    return my_pow(x, mod - 2, mod);
}

int main(){
    long long N, M;
    cin >> N >> M;
    vector<long long> A(N);
    for (long long i = 0; i < N; i++){
        cin >> A[i];
    }

    vector<long long> count(11, 0);
    for (long long i = 0; i < N; i++){
        count[A[i]]++;
    }

    // 階乗と，その逆元を前計算しておく．
    vector<long long> fact(N + 1, 0);
    fact[0] = 1;
    for (long long i = 0; i < N; i++){
        fact[i + 1] = (fact[i] * (i + 1)) % p;
    }

    vector<long long> invfact(N + 1, 0);
    for (long long i = 0; i <= N; i++){
        invfact[i] = mod_inv(fact[i], p);
    }

    // 出てくる頻度が少ない順にソートする（定数倍高速化のため）．
    vector<pair<long long, long long>> pr(10);
    for (long long i = 1; i <= 10; i++){
        pr[i - 1] = pair<long long, long long>(count[i], i);
    }
    sort(pr.begin(), pr.end());

    // dp0[j]: 総和 j で偶数個選ぶ方法の数．dp1[j]: 総和 j で奇数個選ぶ方法の数．
    // dp 配列は必要な領域だけ確保して，必要になる度に追加していくようにする．
    vector<long long> dp0(1, 0);
    vector<long long> dp1(1, 0);
    dp0[0] = 1;

    vector<long long> tmp0(1, 0);
    vector<long long> tmp1(1, 0);

    long long now_sum = 0;
    for (long long i = 0; i < 10; i++){
        long long cnt = pr[i].first;
        long long num = pr[i].second;
        now_sum += cnt * num;
        // 必要になった dp 配列を確保しておく．
        for (long long j = 0; j < cnt * num; j++){
            if (dp0.size() > M){
                continue;
            }
            dp0.push_back(0);
            dp1.push_back(0);
            tmp0.push_back(0);
            tmp1.push_back(0);
        }
        if (cnt == 0){
            continue;
        }
        for (long long j = 0; j <= cnt; j++){
            if (num * j > M){
                continue;
            }
            // 選ぶ組み合わせの数の計算
            if (j % 2 == 0){
                tmp0[num * j] = (fact[cnt] * ((invfact[j] * invfact[cnt - j]) % p)) % p;
            }
            else{
                tmp1[num * j] = (fact[cnt] * ((invfact[j] * invfact[cnt - j]) % p)) % p;
            }
        }

        // 4 通りの全てのパターンに対して NTT．
        vector<long long> conv00 = convolution<998244353>(dp0, tmp0);
        vector<long long> conv01 = convolution<998244353>(dp0, tmp1);
        vector<long long> conv10 = convolution<998244353>(dp1, tmp0);
        vector<long long> conv11 = convolution<998244353>(dp1, tmp1);

        for (long long j = 0; j < dp0.size(); j++){
            dp0[j] = (conv00[j] + conv11[j]) % p;
            dp1[j] = (conv01[j] + conv10[j]) % p;
            tmp0[j] = 0;
            tmp1[j] = 0;
        }
    }
    // 全ての総和が M に満たなければ自動的に 0 通り
    if (now_sum < M){
        cout << 0 << endl;
    }
    else{
        cout << dp1[M] << endl;
    }
}

12. こんな時どうする？

FFT・NTT を用いる際に，ここまでの記事の内容ではまかないきれないような特殊な要求がなされることがあります．その際にはどうすればよいのか，軽く取り上げます．

12-1. 値が絶妙に 64 ビット型の整数にぎりぎり収まるくらいの値で FFT・NTT がしたい¹⁷

この場合はけっこう面倒です．FFT でも NTT でも問題が発生してしまい，どっちつかずなことになってしまうからです．

• FFT を使った場合：小数誤差があるので正しく求められない．
• NTT を使った場合：mod で割った余りしか求められない．

そこで，次のような中国剰余定理を活用しましょう．

$p_i$ をどの $2$ つも互いに素な $n$ 個の整数であるとする．このとき，$n$ 本の式 $x \equiv r_i \pmod {p_i}$ を全て満たすような $x$ が，$0 \leq x < p_1p_2 \cdots p_n$ の範囲に必ず一つ存在する．

これを用いると，例えば複数の mod を用いて NTT を行い，その結果からほしい値を中国剰余定理で求める，といったことが考えられます．

NTT でよく使われる mod には，$998244353$ の他にも，$167772161 (= 5 \times 2^{25} + 1)$ や，$469762049 (= 7 \times 2^{26}+1)$ などがあります．¹⁸これらの mod から NTT を行い，中国剰余定理でほしい値を復元しましょう．

12-2. 10^9 + 7 など，一般の mod での NTT を求めたい

こちらはあまり要求される機会はないとは思いますが，たまに意地悪な問題だと要求される可能性があるかもしれません．

先程の場合と同じく，中国剰余定理で......とやりたくなってしまうかもしれませんが，直接やると答えの桁数が膨大になってしまうような場合に到底対処できません．

中国剰余定理の代わりに，Garnerのアルゴリズムを用います（詳細は省略しますので，興味のある方は調べてみてください）．

おわりに

本記事で述べられなかったトピックの一部の例を，以下に挙げます．興味のある方はぜひ調べてみてください．

• FFT における「ビットリバース」の話．
• 非再帰で FFT・NTT を実装する方法．（Cooley-Tukey のアルゴリズムなどと呼ばれている方法があります）
• FFT・NTT の実装における，定数倍高速化の方法．（本記事で実装例に書いたコードは実はかなり遅いです）
• 小数，mod の値以外で，FFT・NTT と同様な演算が行えるもの．

FFT や NTT などが関わってくる問題はただでさえ難易度がかなり高くなる傾向にありますが，逆に言えば，これを習得できれば高難易度でも解ける問題の幅が広がってくることを意味します．FFT・NTT を学習することは，競技プログラミングの実力向上の役に立つと考えています．

本記事が，FFT・NTT を学習しようと思っている読者の支えとなれば幸いです．

参考文献

FFT（高速フーリエ変換）を完全に理解する話
高速フーリエ変換FFTを理解する
高速フーリエ変換の実装を難しそうかなと思っている方が、なんだ簡単じゃないですか！！ となるための実装講座です
【競プロer向け】FFT を習得しよう！
競プロのための高速フーリエ変換
NTT(数論変換)のやさしい解説
離散フーリエ変換と数論変換 (6) NTT の高速化
任意modでの畳み込み演算をO(n log(n))で
AtCoder Typical Contest 001-C「高速フーリエ変換」解説スライド
「1000000007 で割ったあまり」の求め方を総特集！ 〜 逆元から離散対数まで 〜
原子根の定義と具体例（高校生向け）
中国剰余定理と法が互いに素でない場合への拡張
私用メモ: 畳み込めるものまとめ

1. FFT や NTT は分野によってさまざまな解釈がなされることがありますが，本記事では主に競技プログラミングにおける FFT や NTT の説明を行います． ↩

2. 競技プログラミングをサポートするべく，AtCoder から提供されている，一部のアルゴリズムやデータ構造が収録されているライブラリです． ↩

3. 掃き出し法を用います． ↩

4. オイラーの公式を用いて変形． ↩

5. 「結局元に戻しちゃってるんだから意味ないじゃん！」と思うかもしれませんが，そうではありません．今回の操作で DFT は $A(x)$ と $B(x)$ に対しておこなわれますが，IDFT は $\hat{C}(t)$ に対して行われるということで，DFT を介して多項式を掛け合わせやすい形にしてから IDFT で戻す，というのが肝なのです． ↩

6. マージソートやセグメントツリーの計算量解析がわかる方は，それらを想起してもらえるとわかりやすいかもしれません． ↩

7. double 型の精度は せいぜい $2^{53} \fallingdotseq 10^{16}$ ほどであり，今回のような $10^{18}$ オーダーの計算を必要とする問題ではまるで手に負えません． ↩

8. 「原始根の存在定理　証明」などと検索したら出てくるので，興味のある方は参照してみてください． ↩

9. $r \times r^{-1} \equiv 1 \pmod p$ となるような $r^{-1}$ を，$r$ の $\bmod p$ 上での逆元と呼びます．逆元の求め方は色々ありますが，フェルマーの小定理を用いて $r^{-1} = r^{p-2}$ と求めるやり方がおそらく最も容易に求められるやり方でしょう． ↩

10. AtCoder Library の convolution 関数における制約欄に，「$2^c | (m-1)$ かつ $|a|+|b|-1 \leq 2^c$ なる $c$ が存在する」の文言がありますが，これはここで述べた NTT を行うための $p$ の値の条件と一致します． ↩

11. 通常は $10^5$ オーダー程度で，$10^6$ オーダーくらいが実行時間を考えると限度といったところでしょう． ↩

12. この値が使われるようになった理由は，おそらく 32 ビット整数に収まる値の中で，$10^9$ に近くてキリの良い素数だからという程度の理由なのだろうと思われます． ↩

13. 最近で AtCoder Beginner Contest で mod として $10^9+7$ が登場した回としては， 2022 年 2 月 19 日開催の ABC239 がありますが，直近 $50$ 回の AtCoder Beginner Contest において $10^9+7$ が登場した回はその回のみであり，それ以外での固定 mod は全て $998244353$ となっています． ↩

14. 競技プログラミングにしばしば登場する典型問題を集めたコンテストであり，2021 年 3 月～ 2021 年 7 月にわたって開催されました． ↩

15. 制約を大きくしたのは，愚直解を bitset で高速化する解法が通らないようにするためかと思われます． ↩

16. 実行時間制限が厳しい理由は，愚直な DP 解法を落とすためと思われます． ↩

17. 実はこれに関しては AtCoder Library に搭載されています．atcoder::convolution_ll を用いればよいです． ↩

18. その中で $998244353$ がよく使われるのは，おそらくは $10^9$ にかなり近いため出題しやすい，ということなのではないかと思われます． ↩