Source
Introduction
While many RL agents are capable of achieving significantly higher score than human in some games, their lack of robustness have caused them to fail catastrophically in several harder tasks.
In the figure below, it can be observed that many SOTA algorithms struggle to obtain meaningful scores in the hardest 5th percentile of games.
Despite the advances of reinforcement learning agents throughout the years, they have repeatedly failed at performing well in four games: Montezuma’s Revenge, Pitfall, Solaris and Skiing.
Of the four, Montezuma’s Revenge and Pitfall require extensive exploration to obtain good performance, while Solaris and Skiing are long-term credit assignment problems.
NGU
Recently, a new algorithm named Never Give Up (NGU) was introduced, which expands on the existing R2D2 by using episodic memory. NGU is the first agent to obtain positive rewards, without domain knowledge, on Pitfall. One of the main contribution of NGU is the development of intrinsic motivation rewards to encourage an agent to explore and visit as many states as possible. Within this reward system, two types of rewards can be distinguished: long-term novelty rewards and short-term novelty reward.
Long-term Novelty Rewards
The long-term novelty rewards encourage visiting many states throughout training, across many episodes. This is achieved by using a Random Network Distillation, where a predictor network is constantly being trained to correctly predict the output of a random and untrained convolutional network.
Short-term Novelty Rewards
The short-term novelty rewards encourage visiting many states over a short span of time (e.g., within a single episode of a game). It can be calculated by measuring the distance between the current state and previous states in an episode (note that only features that are important for exploration should be considered, known as controllable states). To achieve this, an embedding network, which composed of two consecutive observations, $x_t$ and $x_{t+1}$, and the action taken by the agent $a_t$, combined with the repeated calculation of the difference between the current state and previous states, yields the short-term novelty reward $r^{episodic}_t$.
Intrinsic Motivation Rewards
NGU mixes these two types of rewards by multiplying both rewards to give a final intrinsic motivation reward as $r^i_t = r^{episodic}_t * min $ { $max$ { $\alpha _t,1 $}$,L$}.
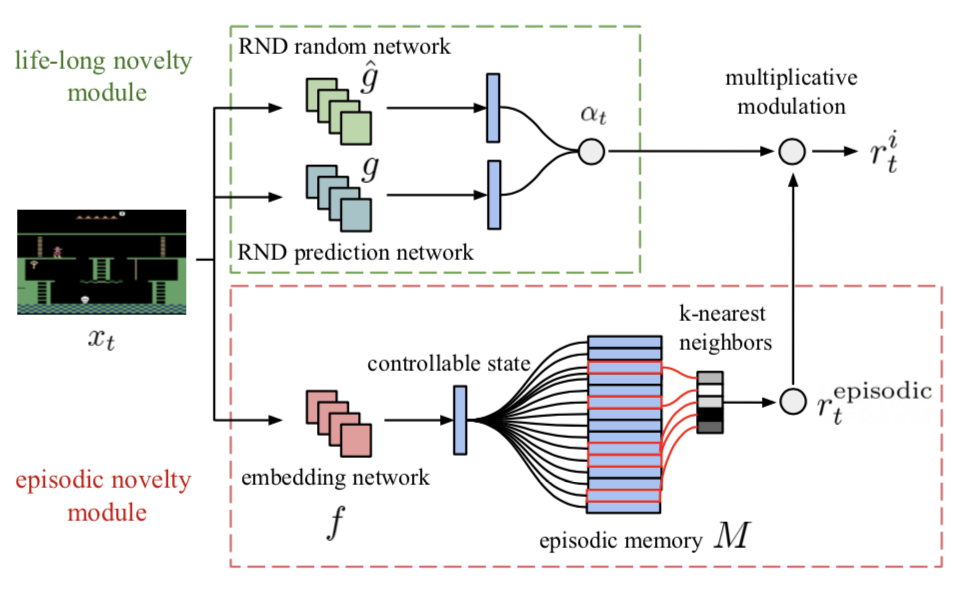
Multiple Policies
Another important concept of NGU is that it learns a collection of policies that range from purely exploitative to highly exploratory. To achieve this, the intrinsic reward is used directly as an input, and the agent maintains an internal state representation that summarizes its history of all inputs (state, action and rewards) within an episode. Each policy has its own augmented reward in the form $r^{\beta_i}_t = r^e_t + \beta_ir^i_t$ that differs from one another based on the value of importance weighting $\beta$ and state-value function discount factor $\gamma$. The experiences are then obtained by sampling uniformly from the list of policies.
Agent57
As effective as NGU is, it has a shortcoming of failing to automatically select the optimal exploration-exploitation trade-off based on the current scenario. For example, a game may require long time horizons to earn important rewards, or perhaps a game may have been fully explored already, yet NGU will continually to sample equally from both exploration and exploitation policies equally. Not only will choosing from sub-optimal actors result in poor performance, but it will also lengthen the total training time by generating redundant replays.
A meta-controller is introduced in Agent57 to adaptively select which policies to use both at training and evaluation time. Networks that better represent state-action value function for the task at hand are now prioritized over others. Furthermore, the calculation of the reward system has been altered through improved parameterization in order to obtain better result.
State-Action Value Function Parameterization
NGU uses one state-action value function $Q(x, a, j, \theta)$ and optimizes on the reward $r_t = r^e + \beta r^i_t$. This method could be problematic especially in cases where the scale and sparseness of $r^e_t$ and $r^i_t$ are both different, or when one reward is more noisy than the other.
To combat this issue, the reward is split into two explicit components:
$Q(x, a, j, \theta)$ = $Q(x, a, j, \theta^i)$ + $Q(x, a, j, \theta^e)$
where $\theta^e$ and $\theta^i$ are the weights of the intrinsic and extrinsic neural networks (identical in architecture) respectively.
During training, both networks would use the same sequence sampled from the replay memory, but are optimized separately. That is, $Q(x, a, j, \theta^i)$ is optimized with $r^i$ while $Q(x, a, j, \theta^e)$ is optimized with $r^e$. Note that both networks still employ the same target policy $\pi(x) = argmax_{\alpha \in {A}}Q(x, a, j, \theta)$, i.e. act greedily based on the output sum from both networks, rather than select from each network independently.
Meta-controller
Another deficiency present in NGU is that while multiple same architecture networks are trained using different pairs of exploration rate and discount factor, $(\beta_j,\gamma_j)$, all policies are trained equally and does not take into account the actual contribution of each policy.
The countermeasure implemented is a meta-controller that uses a N-arm bandit algorithm which runs independently on each actor. Each arm from the N-arm bandit represents one of the policy in the list of policies. At the start of an episode $k$, the meta-controller chooses one of the arm $J_k$, then the $l$-th actor acts $\epsilon_l$-greedily with respect to the corresponding state-action value function, $Q(x, a, J_k, \theta_l )$, for the whole episode. The undiscounted extrinsic episode returns, noted as $R^e_k((J_k)$, are used as a reward signal to train the multi-arm bandit algorithm of the meta-controller.
Because $R^e_k((J_k)$ is non-stationary, as the agent changes throughout training, a simplified sliding window UCB (window size = $\tau$) was utilized in conjunction with random arm selection probability $\epsilon_{UCB} $ for chooseing arm $J_k$ in an episode.
Result
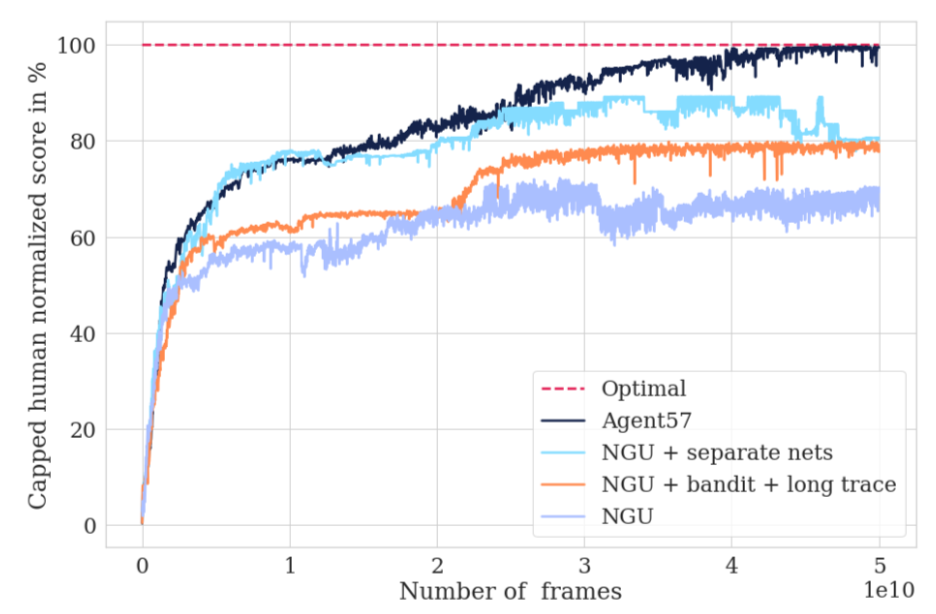
The figure below shows the performance progression on the 10-game challenging set obtained from incorporating each one of the improvements made in Agent57. Out of the ten games, six of them are hard exploration games while four of them are games that require long-term credit assignment.
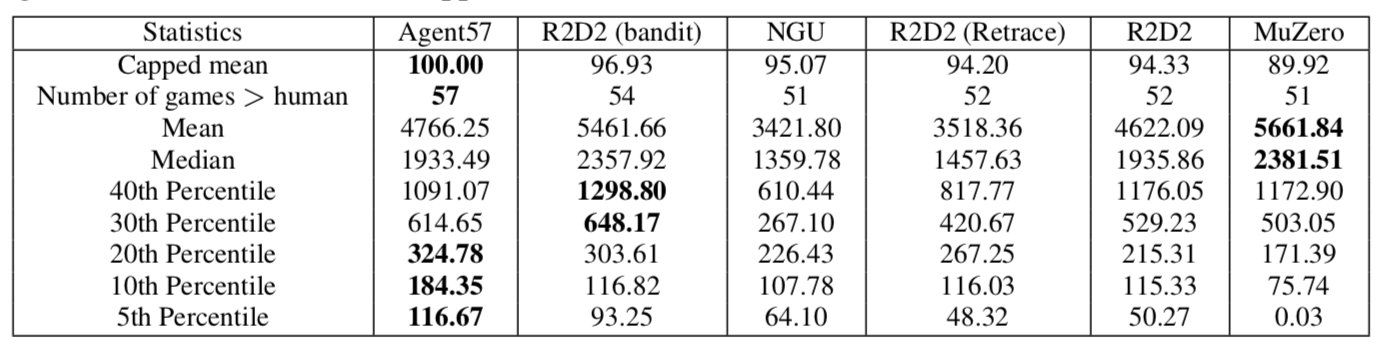
The table displays the performance of Agent57 compared to other RL agents on the 57 Atari games.
Conclusion
The generality of reinforcement agent has been significantly improved by finally scoring more than an average human in all 57 Atari games. However, certain games are still tackled non-optimally as the scores are lower than previous SOTA algorithms. Further enhancements are still required in the representations that Agent57 uses for exploration, planning, and credit assignment.
