Source
Introduction
Reinforcement Learning (RL) has bested human intelligence many times in the past few years in games such as Go and video games. However, there are still very few instances where the strength of RL is utilized in real-world application. Recently, DeepMind has turned their attention to tackle this challenge, and have demonstrated success in optimizing video compression on YouTube.
This paper details the potential of using MuZero in video compression, and has shown that an average 6.28% reduction in size of the compressed videos for the same video quality compared to libvpx, a popular open source VP9 video compression library.
In order to achieve this result, they utilized MuZero as a rate control agent, and combined it with a self-competition based reward mechanism that optimizes a constrained rate control objective.
Algorithm
Overview
In video compression, rate control is a critical component that determines the trade-off between rate (video size) and distortion (video quality) by assigning a quantization parameter (QP) for each frame in the video. A lower QP results in lower distortion (higher quality), but uses more bits. In this paper, we focus on the rate control problem in libvpx, an open source VP9 (a video coding format) codec library. The objective in this setting is to select a QP for each of the video frames to maximize the quality of the encoded video under a bitrate constraint.
Intuitively, the rate control algorithm needs to allocate more bits to complex/dynamic frames and less bits to simple/static frames. This requires the algorithm to understand the rate-distortion tradeoff for each frame and their relationship to the QP values.
VP9 Video Compression
First-pass encoding
The encoder computes statistics (such as average motion prediction error, percentage of zero motion blocks...etc) for every frame in the video, by dividing the frame into non-overlapping 16 × 16 blocks followed by per-block intra and inter-frame prediction (of each block).
Second-pass encoding
The encoder uses the first-pass statistics to decide key-frame locations and insert hidden alternate reference frames. These frames are used as references for encoding other frames, so their encoding quality affects other frames in the video as well. Afterwards, the encoder then starts to encode video frames sequentially.
Based on the decision of a rate controller, a QP value (integer between 0 and 255) is selected for each frame, which governs the quality-rate trade-off.
Constrained Markov Decision Process
Building on top of a normal Markov Decision Process (MDP), which is defined by the tuple $(S, A, P, R, \gamma)$, $k$ constraint functions and their corresponding threshold $\beta_k$ were introduced, forming a Constrained Markov Decision Process (CMDP). The goal is to obtain a policy which maximizes the expected sum of discounted rewards subject to the discounted constraints ($J^{c_k}_\pi$).
The rate control problem can be formulated as a CMDP tuple $(S, A, P, R_{PSNR}, \gamma = 1, c_{Bitrate}, \beta_{Target})$. The state space $S$ consists of the first-pass statistics and the frame information generated by the encoder. The action space $A$ consists of an integer value for QP which is applied to the frame being encoded. The transition function $P(s′|s, a)$ transitions to a new state s′ (next frame to be encoded) given an action a (QP) was executed from state s (current frame being encoded). The bounded reward function ${R_{PSNR}}$ is defined as the PSNR of the encoded video at the final timestep of the episode and 0 otherwise. The constraint function $c_{Bitrate}$ is the bitrate of the encoded video at the final timestep of the episode and 0 otherwise. $\beta_{Target}$ is the user-specified size target for the encoding (256~768 kbps for 480p videos in this paper).
The rate control constrained objective to optimize is defined as:

Self-competition
The agent, referred to as MuZero-Rate-Controller (MuZero-RC), attempts to outperform its own historical performance on the constrained objective over the course of the training. To track the historical performance of the agent, we maintain exponential moving averages (EMA) of PSNR and overshoot (bitrate - target $\beta$) for each unique [video, target bitrate $\beta$] pair over the course of the training in a buffer. When the agent newly encodes a video with a target bitrate $\beta$, the encoder computes the PSNR and overshoot of the episode ($P_{episode}$ and $O_{episode}$ respectively). The agent looks up the historical PSNR and overshoot ($P_{EMA}$ and $O_{EMA}$ respectively) for that [video, target bitrate $\beta$] pair from the buffer. The return for the episode is set to ±1 depending on whether the episode is better than the EMA-based historical performance according to the equation below. The EMAs in the buffer is also updated for the [video, target bitrate $\beta$] pair with $P_{episode}$ and $O_{episode}$.

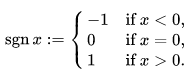
The indicator functions means it will be 1 if the constraint is satisfied, 0 otherwise.
Basically, the agent constantly attempts to beat itself (EMA baseline), and the baseline itself is improved with every EMA update, creating a cycle of performance improvement. Since the performance is measured by comparing bitrate constraint satisfaction first, the agent learns to satisfy the constraint first, and then learns to improve the PSNR.
There is also a small variant of the MuZero-RC agent, which is named Augmented MuZero-RC. This agent is the same as MuZero-RC, except the PSNR term is replaced with $PSNR - 0.005 * overshoot$, in order to get the agent to reduce bitrate if it can’t improve PSNR. The factor of 0.005 was selected as it is roughly the average slope of VP9’s RD curve across the training dataset.
Agent Architecture
The agent is trained in an asynchronous distributed actor-learner setting with experience replay, where a memory buffer for the EMA is shared across all actors. The learner process samples transitions from the experience replay buffer to train the networks, and sends the updated parameters to the actor processes at regular intervals.
Networks
Similar to MuZero, the agent has three subnetworks. The representation network maps the features to an embedding of the state using Transformer-XL encoders and ResNet-V2 style blocks. The dynamics network generates the embedding of the next state given the embedding of the previous state and an action using ResNet-V2 style blocks. Given an embedding, the prediction network computes a policy using a softmax over the QPs, the value of the state, and several auxiliary predictions of the metrics related to the encoding using independent layer-normalised feedforward networks.


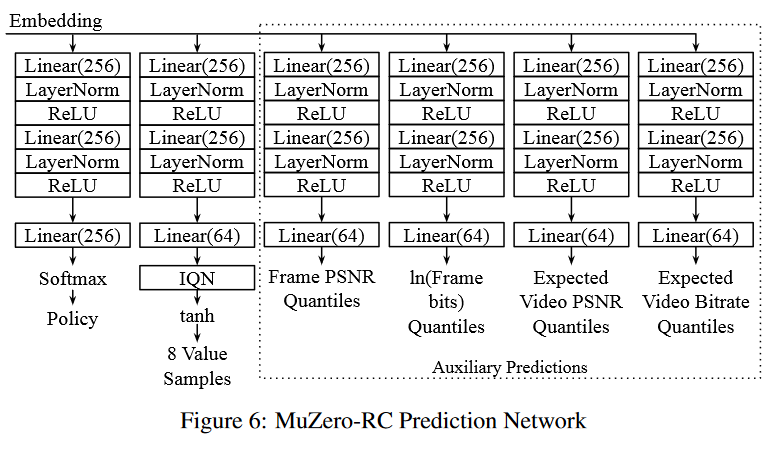
Input Features
The input features contain an observation from the encoder containing first-pass statistics for the video, PSNR and bits for the frames in the video encoded so far, index and type of the next frame to be encoded, and the target bitrate for the encoding.
Losses
At every step in the training, the learner uniformly samples a batch of states, five subsequent actions, and the necessary labels from the experience replay buffer. The representation network generates the embedding of the state, and the dynamics network is unrolled five times to generate the subsequent embeddings. The prediction network outputs the predictions for policy, value, and auxiliary metrics for the current and the five subsequent states. The policy prediction $\hat{\pi}_t$ is trained to match the MCTS policy generated at acting time $\pi_t$ using cross-entropy loss. The value prediction $\hat{v}_t$ is trained to match the self-competition reward $v_t$ for the episode using IQN loss, and the auxiliary predictions $\hat{y}_t$ are trained to match the corresponding metrics $y_t$ using a quantile regression loss. The combined loss is as follow:

Result
Dataset
The experiments focuses on 480p videos with target bitrate in [256, 768] kbps range, although the proposed methods can be generalised to other resolutions and bitrates.
For training, they used 20,000 randomly selected 480p videos that have varying duration (3 to 7 seconds), varying aspect ratios, varying frame rates, and diverse content types. The target bitrate for training is uniformly sampled from {256, 384, 512, 640, 768} kbps.
For evaluation, videos with resolution 480p and higher from the YouTube UGC dataset were used. The videos are resized to 480p, and sliced into 5-second clips, resulting in 3062 clips.
Metrics
The Bjontegaard delta rate (BD-rate) is used to evaluate the coding efficiency and overall bitrate reduction. Given the bitrate v.s. PSNR curves of two policies, BD-rate computes the average bitrate difference for the same PSNR across the overlapped PSNR range, and therefore, measures the average bitrate reduction for encoding videos at the same quality.

Evaluation
Instead of performing MCTS, the QPs with the highest probability assigned by the policy output of the prediction network are selected. Each video is encoded at nine target bitrate values uniformly spaced between [256, 768] kbps.
PSNR BD-Rate improvement
The BD-Rate imporvement for MuZero-RC compared to the libvpx baseline can be seen below.

MuZero-RC not only overshoots less, but it also tends to fully use the target bitrate budget more frequently compared to libvpx.
MuZero-RC avoids overshooting by using fewer bits (and thus sacrificing the PSNR) in early frames of the video as shown in (b). This is a good decision because the PSNR of the first part of the video is already relatively high.
The figure below shows examples where MuZero-RC achieves better BD-rate.
In (a), MuZero-RC sacrifices the PSNR of the first 60 frames in order to improve the PSNR of the rest of the frames. Because the latter part of the video is more complex (indicated by lower PSNR), improving the PSNR of the latter part of the video improves the overall PSNR.
In (b), MuZero-RC boosts PSNR of a reference frame, leading to significant PSNR improvement for all the frames following that frame.
In (c), the video has a scene change towards the very end. Because libvpx runs out of bitrate budget, it decides to encode the last few frames with low quality. In contrast, MuZero-RC correctly anticipates the scene change, and saves some bitrate budget from the first 140 frames so that it can obtain a
reasonable PSNR for the last few frames.
(d) shows another pattern where MuZero-RC has overall less frame PSNR fluctuation. In particular, it avoids having extremely low PSNR on some
frames, which in turn improves the overall PSNR.

Conclusion
In this paper, reinforcement learning has been successfully applied to optimize a real-world problem. Considering the amount of videos that are streamed daily, a 6% saving in bit rate is actually a tremendous amount.
I am curious about the result of MuZero-RC when applied to videos of higher quality, as most videos nowadays are at least 720p. In addition, I am also interested to see whether the agent perform better or worse when given longer length videos.