チーム打率とチーム得点の関係
2018年のプロ野球のペナントレースの、約1/4が終了した(2018/05/16現在)。
今シーズンのペナントレースは、例年以上にチーム間の得点力の差が顕著に現れている。
そして、
「あの埼玉の山賊打線はチーム打率が~~」
みたいな話がネット上でよく話題になっている。
しかし、チーム打率は本当にそのチームの得点力を反映しているのだろうか?
実際のデータを見てみよう。
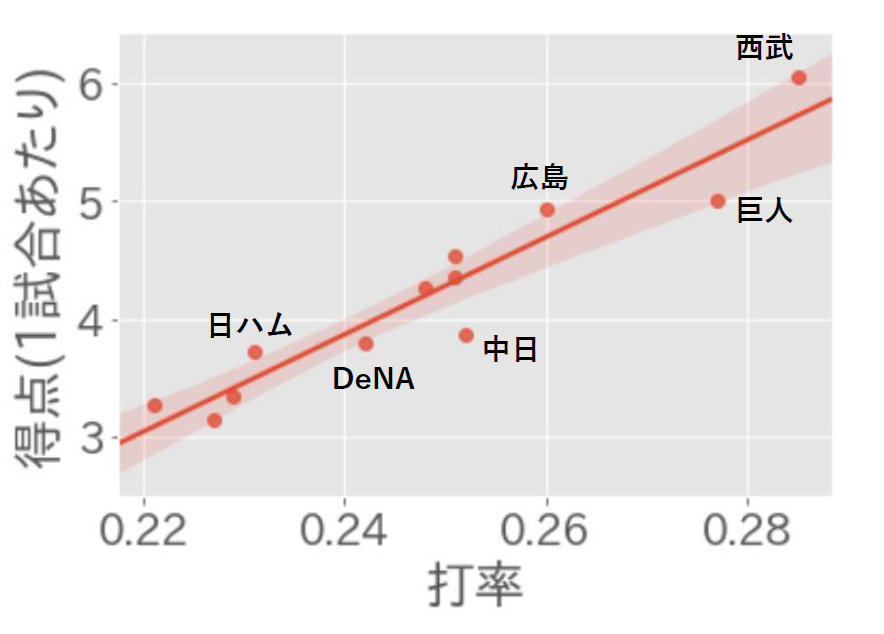
2018/05/15の試合前時点での、12球団の「チーム打率」と「チーム得点(1試合あたり)」の散布図である。
線は回帰直線を表している。
すると、概ね「打率が高いチームほどよく得点している」という傾向が見て取れるが、
- 広島と巨人
- 日ハムとDeNAと中日
など、「チーム打率は大きく違うのに、得点力はほぼ同じ」であるような組み合わせがいくつか存在していることが分かる。
チーム打率は、本当にそのチームの得点力に影響しているのだろうか?
そこで、RVM(Relevance Vector Machine)を用いて、「チームの得点力に直接影響している指標は何か」を暴き出すことにした。
RVM(Relevance Vector Machine)について
RVM(Relevance Vector Machine、またの名を「関連ベクトルマシン」)についての解説。
以降、データは
\phi({\bf x}_{n}) = (x_{(n, 1)}, ..., x_{(n, M-1)}, 1)^T\in \mathbb{ R }^M (n = 1, …, N) \\
t_{n}\in \mathbb{ R } (n = 1, …, N)
が手元に与えられている状態とする。
また、$\Phi$を以下のように定義する。
\Phi = \left( \begin{array}{ccccc} \phi({\bf x}_{1})^T \\ \vdots \\ \phi({\bf x}_{i})^T \\ \vdots \\ \phi({\bf x}_{N})^T\end{array}\right) \in \mathbb{ R }^{N \times M}
通常の線形回帰モデル
通常の線形回帰モデルでは、
p(t|{\bf x}, {\bf w}, \beta) = N(t|y({\bf x}), \beta^{-1}) \\
y({\bf x}) = {\bf w}^T\phi({\bf x})
として、パラメータ${\bf w}\in \mathbb{ R }^M$を学習する。
ベイズ的にパラメータ${\bf w}$の事後分布を求めたいときには、ハイパーパラメータ$\alpha\in \mathbb{ R }$を用いて、${\bf w}$の事前分布を
p(w_{i}|\alpha) = N(w_{i}|0, \alpha^{-1})
のようにして定義し、以下の計算によって${\bf w}$の事後分布を求める。
p({\bf w}|{\bf t}, {\bf X}, \alpha, \beta) \propto p({\bf t}|{\bf w}, {\bf X}, \beta) p({\bf w}|\alpha)
RVMを用いた回帰モデル
それに対して、RVMによる回帰モデルでは、上記の2つ目の式を
y({\bf x}) = \sum_{n=1}^{N} w_{n}k({\bf x}, {\bf x}_{n})+ b
として、パラメータ${\bf w}\in \mathbb{ R }^N$(と$b$)を学習する($k$はカーネル関数)。
また、パラメータ${\bf w}$の事前分布を、${\bf \alpha}\in \mathbb{ R }^N$を用いて以下で与えてやる。
p({\bf w}|{\bf \alpha}) = \prod_{n=1}^{N} N(w_{n}|0, \alpha_{n}^{-1})
RVMの大きな特徴として、この${\bf \alpha}$についても学習(周辺尤度を最大にするように最適化)を行い、最適な値を求める(詳しくは後述)。
後述の通り、「周辺尤度をなるべく大きくする${\bf \alpha}$」を求めていくのだが、実際に最適化を行うと、{${\alpha}_{n}$}の一部は非常に大きな値になることが知られている。このとき、対応する$w_{n}$は、平均・分散ともに0の事後分布を持つことになるので、
y({\bf x}) = \sum_{n=1}^{N} w_{n}k({\bf x}, {\bf x}_{n})+ b
を考えた場合、この0になった$w_{n}$に対応するカーネル関数の値$k({{\bf x}, {\bf x}_{n}})$はモデルから取り除かれ、新しい入力に対する予測に対して全く影響を及ぼさなくなる。
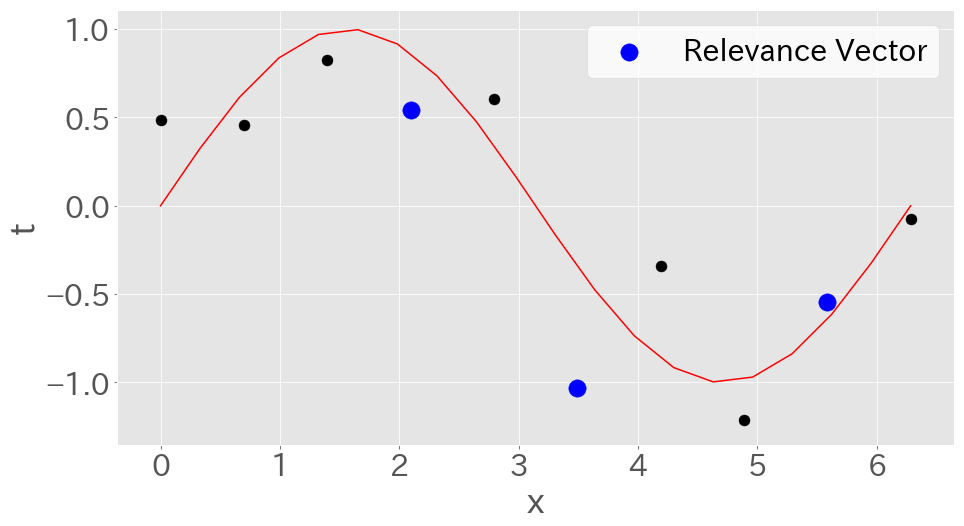
一方で、ゼロでないカーネル関数$k({\bf x}, {\bf x}_{n})$に対応する${\bf x}_{n}$は関連ベクトル(Relevance Vector)と呼ばれる。
新しい入力に対する予測は、この関連ベクトルをだけを用いて行うことができる。
(SVM(Support Vector Machine)が、新しい入力に対する予測をサポートベクトル(Support Vector)だけで行うことが出来るのと似ている)
RVMのアレンジ
RVMでも、通常の線形回帰モデルのように、
y({\bf x}) = {\bf w}^T\phi({\bf x})
として、パラメータ${\bf w}\in \mathbb{ R }^M$を学習させても良い。
この場合、$w_{i}$の事前分布は
p({\bf w}|{\bf \alpha}) = \prod_{i=1}^{M} N(w_{i}|0, \alpha_{i}^{-1})
で与え、1つの特徴量(説明変数)、すなわち
(\phi({\bf x_{1}})_{i}, ..., \phi({\bf x_{n}})_{i}, ... , \phi({\bf x_{N}})_{i})^T \in \mathbb{ R }^{N}
が、1つの関連ベクトルに対応している。
すなわち、$\alpha_{i}$が取り除かれるたびに、モデルから1つの特徴量(説明変数)が取り除かれるため、重要でない特徴量が取り除かれた、疎なモデルを得ることが出来る。
(疎なモデルを得ることが出来る手法としてはLassoが有名だが、Lassoだと、「どれくらい疎にするか」を制御するハイパーパラメータ$\lambda$の値をチューニングといけない。RVMではハイパーパラメータも最適化してくれるため、チューニングは必要ない。)
RVMの学習
事前に{${\bf \alpha}, \beta$}を適当な値で初期化しておいた上で、
以下のようなサイクルで、{${\bf \alpha}, \beta, {\bf w}$}の3種類のパラメータの学習を行う。
1. wに関する最適化
{${\bf \alpha}, \beta$}を固定して、${\bf w}$の事後分布
p({\bf w}|{\bf t}, \Phi, {\bf \alpha}, \beta) = N({\bf w}|{\bf m}, \Sigma)
の${\bf m}$と$\Sigma$を求める。
${\bf m}$と$\Sigma$はそれぞれ以下の通りとなる。
{\bf m} = \beta \Sigma \Phi^T \ {\bf t} \\
\Sigma = (A + \beta \Phi^T \Phi)^{-1}
ただし、
A = \left(
\begin{array}{ccccc}
\alpha_{1} &
0 & \cdots & \cdots &
0\\
0 & \ddots & & & \vdots \\
\vdots & &
\alpha_{i} & &
\vdots \\
\vdots & & & \ddots & 0 \\
0 & \cdots &
\cdots & 0 &
\alpha_{M} \end{array}
\right)
2. α, βに関する最適化
{${\bf m}, \Sigma$}を固定して、周辺尤度
p({\bf t}|\Phi, {\bf \alpha}, \beta) = \int p({\bf t}|\Phi, {\bf w}, \beta) p({\bf w}|{\bf \alpha}) d{\bf w}
を最大にする${\bf \alpha}$と$\beta$を求める。
上記の式は、対数をとって書き下すと以下の通りとなる。
\begin{eqnarray}
\ln p({\bf t} | \Phi, {\bf \alpha}, \beta) &=& \ln N({\bf t} | {\bf 0}, C) \\ &=& -\frac{1}{2} \{N \ln (2\pi) + \ln |C| + {\bf t}^TC^{-1}{\bf t}\}
\end{eqnarray}
ただし、
C = \beta^{-1} I + \Phi A^{-1} \Phi^T
この式の微分を0とすると、$\alpha_{i}$、$\beta$に関して、以下の値が得られる。
(\beta^{new})^{-1} = \frac{{\|{\bf t} - {\bf \Phi m} \|}^2}{N - \Sigma_{i} \gamma_{i} } \\
{\alpha_{i}}^{new} = \frac{\gamma_{i}}{m_{i}^2}
ただし、
\gamma_{i} = 1 - \alpha_{i}\Sigma_{ii}
これにより、$\alpha_{i}$、$\beta$の値がアップデートされる。
また、この処理によってある$\alpha_{i}$が無限大に発散していたら、その$\alpha_{i}$とそれに対応する$w_{i}$と$\phi({\bf x})_{i}$を取り除く。
($\alpha_{i}$が1つ取り除かれるたびに、${\bf w}$、${\bf m}$、$\Sigma$、$\phi({\bf x}_{n})$のsizeはそれぞれ1小さくなる)
上記の1. と2. を、収束するまで繰り返す。
収束したときの${\bf m}$を${\bf m^{*}}$とすると、新しい入力$\hat{{\bf x}}$に対する予測値$\hat{t}$は、以下の式で得ることが出来る。
\hat{t} = {\bf m}^{*T}\phi(\hat{{\bf x}})
(もちろん$\hat{t}$は点推定でなく分布も算出することが出来るが、ここでは省略)
何故αが無限大に発散するのか
何故特定の$\alpha_{i}$が発散するのかに関する大雑把な解釈。
ある$\alpha_{i}$が大きな値をとったとする。この時、
p(w_{i} | \alpha_{i}) = N(w_{i} | 0, \alpha_{i}^{-1})
より、$w_{i}$はゼロに寄った事前分布を取るということが分かる。よって、この状態から$\alpha_{i}$を固定して$w_{i}$の事後分布を求めると、その分布もゼロに寄る、つまり$m_{i}$は小さな値を取るということになる。
続いて${\bf m}$、$\Sigma$を固定して$\alpha_{i}$の最適化を行うが、この時、上記の$\alpha_{i}$のアップデートの式より、$m_{i}$が小さいと$\alpha_{i}$はますます大きくなる。
以上の、
- $\alpha_{i}$が大きいと$m_{i}$は小さくなる
- $m_{i}$が小さいと$\alpha_{i}$が大きくなる
という正のフィードバックにより、一部の$\alpha_{i}$が無限大に発散する。
RVMのメリット
- 交差検証不要、自動で最適なハイパーパラメータの値が決まる
- Lassoのように、自動で変数選択してくれる
- モデルのパラメータを点推定しているのでなく、分布が求まる
- wの各要素ごとに事前分布のハイパーパラメータのアップデートを行うので、「全ての特徴量で値のオーダーを統一」したり「特徴量毎にデータを正規化」したりといった、前処理をする必要がない
RVMのデメリット
- 計算コストが高い
- 特に、${\bf w}$の分布をアップデートのために逆行列の計算を複数回しなければならない
RVMのコード
RVMをpythonのnumpyを用いて実装した。コードは以下の通り。
from abc import ABCMeta, abstractmethod
import numpy as np
def mean_squared_error(y, t):
return np.mean((y - t)**2)
def rmse(y, t):
return np.sqrt(np.mean((y - t) ** 2))
class MachineLearningModel(metaclass=ABCMeta):
@abstractmethod
def fit(self, data, target, **kwargs):
# モデルの学習関数
pass
@abstractmethod
def predict(self, data, **kwargs):
# モデルの予測関数
pass
class RegressionModel(MachineLearningModel):
"""
回帰モデル。GLMでいうところの、「指数型分布:ガウス分布」に対応するモデル。
"""
@abstractmethod
def _forward(self, data):
pass
def predict(self, data):
return self._forward(data)
def rmse(self, data, target):
y = self.predict(data)
return rmse(y, target)
def loss(self, data, target):
y = self.predict(data)
return mean_squared_error(y, target)
class RelevanceVectorMachine(RegressionModel):
def __init__(self, initial_alpha=1e-2, initial_beta=1e-2):
self.alpha = initial_alpha
self.beta = initial_beta
self.inf = 1e10 # この値より大きくなったら、無限大とみなす。
self.Cov = None
self.m = None
self.bool_arr_for_pred = None
self.Phi = None
self.M = None
self._PhiTPhi = None
self.itr = None
def _update_mean_and_cov(self, target):
"""
alpha, betaを固定して、m, Σのアップデートを行う
"""
A = np.diag(self.alpha)
self.Cov = np.linalg.inv(A + self.beta * self._PhiTPhi)
self.m = self.beta * self.Cov @ self.Phi.T @ target
def _update_alphabeta(self, target, N):
"""
m, Σを固定して、alpha, betaのアップデートを行う
"""
gamma = 1 - self.alpha * np.diag(self.Cov)
self.beta = (N - np.sum(gamma)) / \
np.sum((target - self.Phi @ self.m)**2)
self.alpha = gamma / (self.m ** 2)
def _remove_inf(self, verbose):
"""
alphaが無限大に飛んだときそこに対応する特徴量を削減する
"""
bool_arr = self.alpha <= self.inf
if np.sum(bool_arr) == self.M:
# どのalphaも無限大に飛ばなかったとき、そのまま
return
# 無限大に飛ばなかったものだけを残す
self.alpha = self.alpha[bool_arr]
self.Phi = self.Phi.T[bool_arr].T
self.Cov = self.Cov[bool_arr].T[bool_arr].T
self._PhiTPhi = self.Phi.T @ self.Phi
self.m = self.m[bool_arr]
# 予測のためのbool_arrをかきなおす。
# bool_arrは、無限に飛んだ特徴量が出るたびにsizeが小さくなってしまうので、
# 新規にデータに対して予測を行うために、
# sizeが維持された配列をもうひとつ用意する必要がある。それがbool_arr_for_pred
assert len(bool_arr) == np.sum(self.bool_arr_for_pred)
# where : bool_arr_for_predの中で、未だにTrueである要素のインデックス
where = np.where(self.bool_arr_for_pred)[0]
# for i in range(self.M):
# if not bool_arr[i]:
# self.bool_arr_for_pred[where[i]] = False
# if verbose:
# print(where[i], "番目の要素が削除されました")
# 上記のfor loopありのコードを最適化すると以下のとおりになる。
ind = where[np.arange(self.M)[np.logical_not(bool_arr)]]
self.bool_arr_for_pred[ind] = False
if verbose:
for i in ind:
print(i, "番目の要素が削除されました")
self.M = np.sum(bool_arr).astype(int)
def fit(self, data, target, patience=1e-4, random_state=None, verbose=False):
"""
Nがデータ数。
self.Mが特徴量の数。
"""
if random_state is not None:
np.random.seed(random_state)
# 切片を加えます。
self.Phi = np.c_[np.array(data), np.ones(len(data))]
self._PhiTPhi = self.Phi.T @ self.Phi
N = len(data)
self.M = self.Phi.shape[1]
self.alpha = np.ones(self.M) * self.alpha
self.Cov = np.random.randn(self.M, self.M)
self.m = np.random.randn(self.M)
self.bool_arr_for_pred = np.ones(self.M).astype(bool)
self.itr = 0
while True:
prev_beta = self.beta
self._update_alphabeta(target, N)
self._update_mean_and_cov(target)
self._remove_inf(verbose)
self.itr += 1
if abs(self.beta - prev_beta) < patience:
# betaが収束した時に
break
def _forward(self, data):
# 切片を加えます。
Phi = np.c_[np.array(data), np.ones(len(data))]
return Phi.T[self.bool_arr_for_pred].T @ self.m
RVMでチーム得点数を予測するモデルの作成
RVMを使って、プロ野球のチーム得点数を予測するモデルの作成することにした。
具体的には、説明変数をチームの1シーズンの「打率」「出塁率」「本塁打数」などにして、目的変数をチームの1シーズンの「得点数」とするモデルを作成した。
RVMを学習させる過程で関連ベクトルから除外された(つまり対応する$\alpha_{i}$が無限大に発散した)説明変数は、チームの得点に影響を与えない、という解釈をすることが出来る。
データの取得
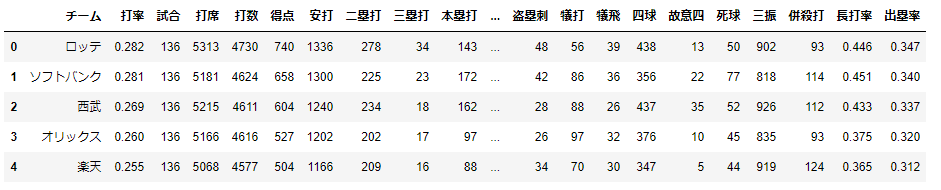
データは、NPB公式サイト内の年毎のチーム成績のページ(http://npb.jp/bis/2017/stats/tmb_p.htmlなど)から、pandasのread_html関数を用いてスクレイピングで取得した。
取得したのは、2005年から2017年の13年間の、セパ12球団のチーム成績データ。
import pandas as pd
yrange = range(2005, 2017 + 1)
lst_of_df = []
for year in yrange:
print("year : ", year)
for league in ['p', 'c']:
url = 'http://npb.jp/bis/'+str(year)+'/stats/tmb_'+league+'.html'
lst_of_df.append(pd.read_html(url, header=0)[0])
# データ内の数字データのtypeをfloatあるいはintに変換
df = pd.concat(lst_of_df).set_index("チーム").apply(pd.to_numeric).reset_index()
# カラム名からスペースを除く
df.columns = list(map(lambda v : v.replace("\u3000", ""), df.columns))
# チーム名からスペースを除く
df['チーム'] = list(map(lambda v : v.replace("\u3000", "").replace(" ", ""), df['チーム']))
# 横浜ベイスターズの表記を統一
df.loc[df['チーム'] == '横浜', 'チーム'] = '横浜(DeNA)'
df.loc[df['チーム'] == 'DeNA', 'チーム'] = '横浜(DeNA)'
モデルの学習
このデータを、モデルに学習させる。
なお、得点に効いている特徴量の候補として、
- 打率
- 出塁率
- 長打率
- 犠打
- 盗塁
- 本塁打
以上の6つの特徴量の値を線形結合したものを、$\phi({\bf x})$とした。
(つまり、interceptも含めると、$M=7$)
import pandas as pd
from sklearn.model_selection import train_test_split
# データの取得
x_cols = [
'打率',
'出塁率',
'長打率',
'犠打',
'盗塁',
'本塁打'
]
# データ全体の25%をテスト用データとする
datax = df.loc[:, x_cols]
datat = df['得点']
x_train, x_test, y_train, y_test = train_test_split(datax, datat, test_size=0.25, random_state=1)
y_train = np.array(y_train)
y_test = np.array(y_test)
# モデルによる予測
inf = 1e10
model = RelevanceVectorMachine()
model.inf = inf
model.fit(x_train, y_train, random_state=0,
patience=1e-10, verbose=True)
y_pred = model.predict(x_test)
# 予測結果の出力
x_cols_with_intercept = np.array(x_cols + ['intercept'])
for u, v in zip(x_cols_with_intercept[model.bool_arr_for_pred], model.alpha):
print(u, "{0:04f}".format(v))
print("")
print("iteration n:", model.itr)
学習結果
出力結果は以下の通りとなった。
(数字は、各要素に対応する$\alpha_{i}$の値)
0 番目の要素が削除されました
出塁率 0.000000
長打率 0.000001
犠打 1264.965992
盗塁 36.137813
本塁打 5.498206
intercept 0.000002
iteration n: 87
なんと、打率が「予測に不必要な値(つまり関連ベクトルでない)」と判断されて除外された。
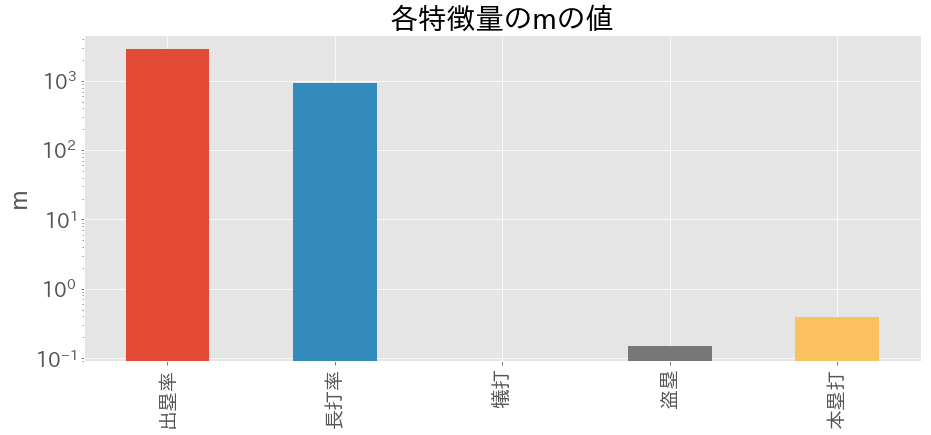
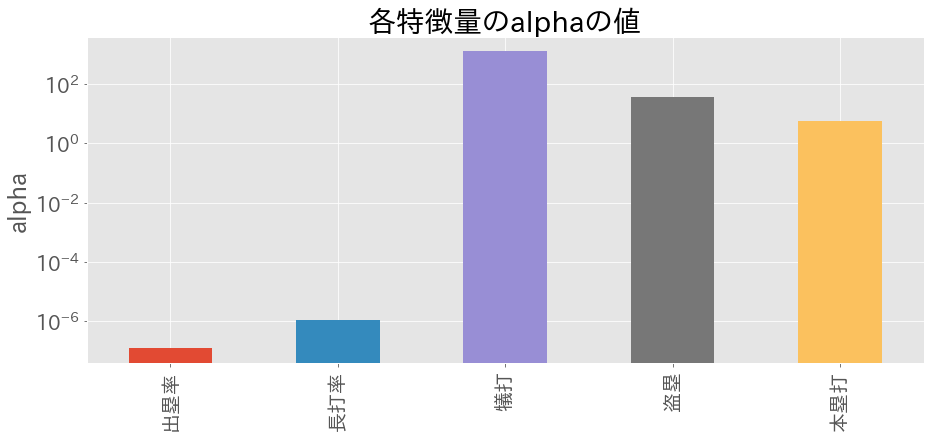
各要素に対応する$m_{i}$($w_{i}$の事後分布の平均値)、$\alpha_{i}$の値をそれぞれ図示すると以下の通りとなった(y軸がlogスケールになっているので注意)。
from collections import OrderedDict
df_fet = pd.DataFrame(OrderedDict({'m': model.m[:-1], 'alpha': model.alpha[:-1]}))
df_fet.index = np.array(x_cols)[model.bool_arr_for_pred[:-1]]
df_fet.columns = ['m', 'alpha']
for var in ['m', 'alpha']:
plt.figure(figsize=(15,6))
df_fet[var].plot.bar()
plt.title("各特徴量の"+var+"の値")
plt.ylabel(var)
plt.yscale('log')
plt.show()
$\alpha_{i}$が大きいほど、対応する$m_{i}$の絶対値は小さい、という対応が見て取れる。
大雑把に解釈するならば、
- $\alpha_{i}$が大きいと、$p(w_{i}|\alpha_{i}) = N(w_{i}|0, \alpha_{i}^{-1})$より、$w_{i}$の事前分布は「平均0・分散0」の正規分布に従う。すなわち$w_{i}$の事後分布は0によった形になるので、$m_{i}$も0に近い値となる
ということになる。
打率以外の5つの特徴量を大きく2つに分類すると、以下のような結果となった。
| 説明変数 | $m_{i}$ | $\alpha_{i}$ | 得点(目的変数)への影響 |
|---|---|---|---|
| 出塁率、長打率 | 大きい | 小さい | 大きい |
| 犠打、盗塁、本塁打 | 小さい | 大きい | 小さい |
つまり、チームの得点は、(少なくとも上記の6つの特徴量の中では)出塁率と長打率の2つが効いていて、それ以外の4つの特徴量は得点に対してほとんど影響を及ぼさないということがわかった。
(なお、random_seedを何通りか試したが、どの場合でも、打率に対応する$\alpha_{i}$は無限大に発散するか、非常に大きな値となった)
予測結果
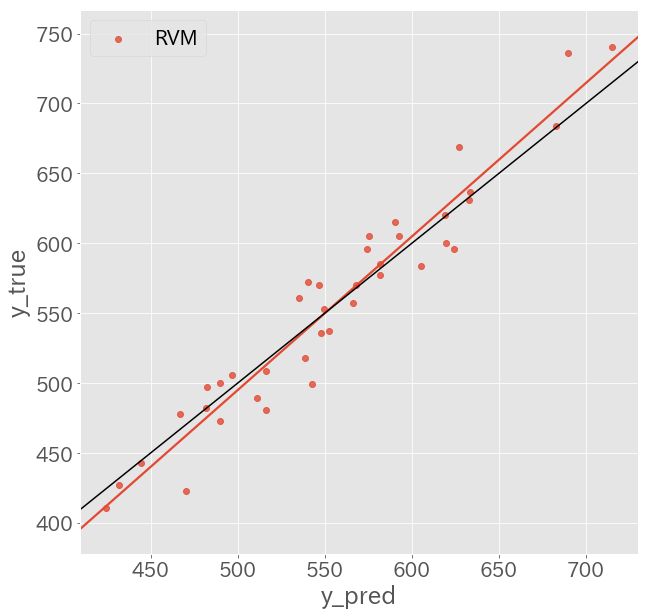
テストデータに対して予測を行い、
- モデルの予測した得点を横軸
- 実際の得点を縦軸
にとって図示すると、以下の通りとなった。
import seaborn as sns
y_pred = model.predict(x_test)
rmse(y_pred, y_test)
plt.figure(figsize=(10, 10))
ax = sns.regplot('y_pred', 'y_true', pd.DataFrame({"y_true":y_test, "y_pred": y_pred}), ci=None, label='RVM')
ax.legend(loc="best")
plt.plot(np.arange(400, 750), np.arange(400, 750), color='k')
1つの赤点は「1チーム・1シーズン」を表している。
赤線は赤点の回帰直線で、黒線は「y=x」の直線である。
赤線が概ね黒線と一致していることからも、概ねこのモデルで得点が予測できるということが分かる。
テストデータにおけるRMSEは、
rmse_ = model.rmse(x_test, y_test)
print("rmse:", rmse_)
# rmse: 21.739688524489146
約21.7という結果になった。
(因みに、同じデータで、sklearnのLassoCVでも学習を行ったが、Lassoでも同様に打率の係数が0になり、予測RMSEもRVMのものとほぼ同程度の値となった)
まとめ
今回の分析のまとめは以下の通り
- RVM(Relevance Vector Machine)とは、モデルのパラメータ$w_{i}$と、$w_{i}$のハイパーパラメータ$\alpha_{i}$を交互に最適化していく事によって学習させるモデル。
- 無限大に発散する$\alpha_{i}$に対応する$w_{i}$の値は0になるので、Lassoのように疎な解を持つ。
- $w_{i}\ne 0$となった$w_{i}$に対応する$(\phi({\bf x_{1}})_{i}, ..., \phi({\bf x_{n}})_{i}, ... , \phi({\bf x_{N}})_{i})^T \in \mathbb{ R }^{N}$は「関連ベクトル(Relevance Vector)」と呼ばれる。
- 新しいデータに対して、RVMは関連ベクトルだけを用いて予測を行うことが出来る。
- RVMを用いて、プロ野球のチーム得点に効いている特徴量を、RVMを用いて抽出した。その結果、以下のことがわかった。
- 「打率」は関連ベクトルから除外された。すなわち、打率は(少なくとも出塁率や長打率と比べると)得点に対する影響力が小さい。
- 関連ベクトルとして残った特徴量の$m_{i}$の値より、得点は概ね「出塁率」と「長打率」によって決まっている。
因みに断っておくと、「得点に対しては打率よりも出塁率が長打率が重要」というのは新事実でも何でもなく、セイバーメトリクス界隈では有名な話。
詳しくはマネーボール (ハヤカワ・ノンフィクション文庫)が詳しい。
ソースコード
本文献で実行したコードは、以下にアップロードしている。
(※スクレイピングによってデータを取得しているので、2018年度のデータに関してはNPBのページが更新されるたびに異なる結果となるので注意)