半教師あり学習
半教師あり学習に関する基礎的な知識や歴史が分かりやすくまとまっている動画。
https://www.youtube.com/watch?v=Jj_MijO_gzU
https://www.youtube.com/watch?v=7D9i54xvKPw
論文読み
FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence [Kihyuk Sohn+ NIPS20]
https://arxiv.org/abs/2001.07685
Introduction
DNNは多くの場合、ラベルありデータを用いた教師あり学習によってその高い性能を獲得することが出来る。しかしラベリングには人手が必要で大きなコストがかかる。よって大量のラベルを必要とせず、大量のデータからモデルを学習するためのアプローチが半教師あり学習(Semi-supervised Learning,SSL)である。半教師あり学習ではラベルの無いデータを活用することで、ラベル付きデータの必要性を軽減することが出来る。
本研究では複雑な既存手法と比較して単純かつ高精度な手法FixMatchを提案している。FixMatchではconsistency regularizationとpseudo-labelingの両方を用いて疑似ラベルを生成する。ラベルなし画像に弱いデータ拡張(フリップとシフトのみ)を施したものから疑似ラベルを生成し、同じ画像に強いデータ拡張(Cutout,CTAugment,RandAugmentを使用)を施したもののモデル出力がこの疑似ラベルに近づくように学習する。pseudo-labelingのアプローチに従って、モデルが高い確信度を持つときのみ疑似ラベルを保持、使用する。
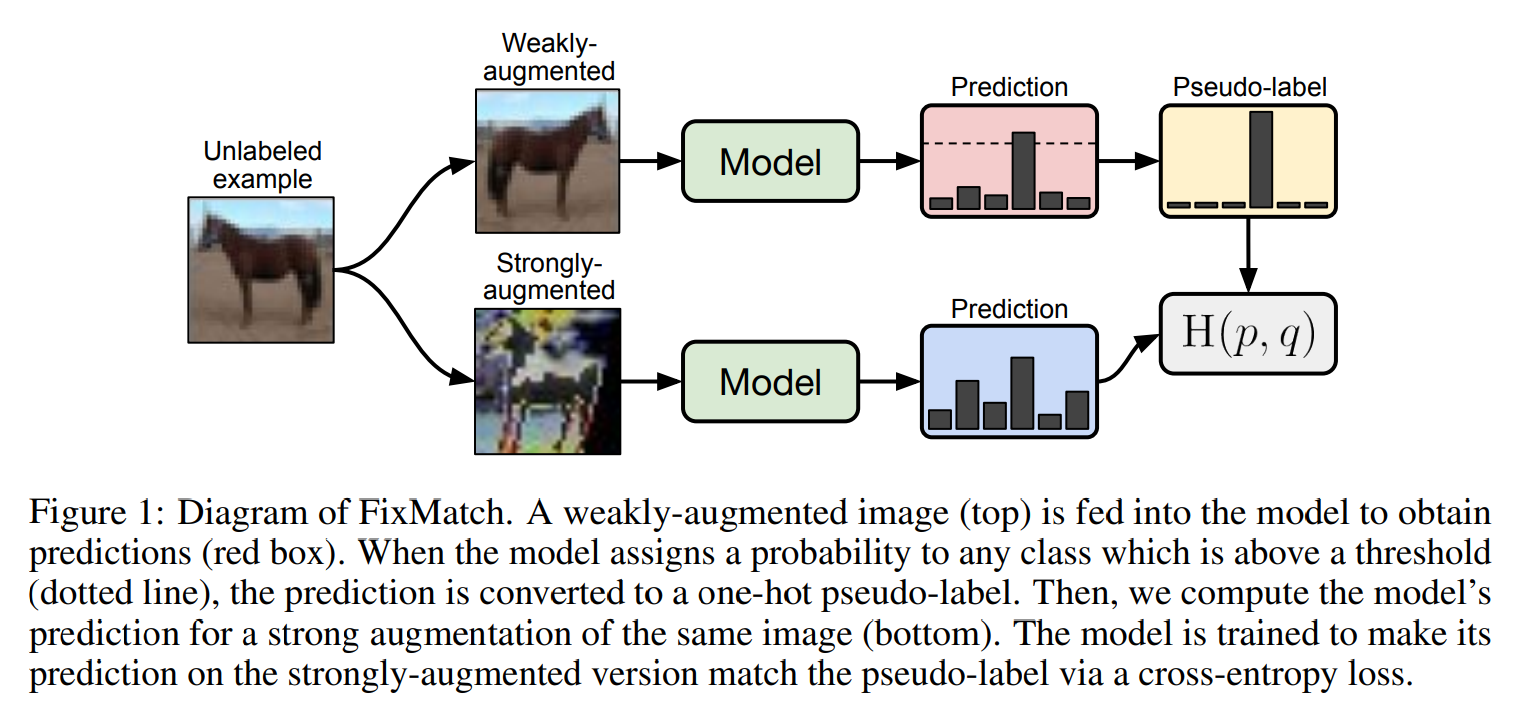
シンプルな機構であるのにもかかわらず、多くのSSLベンチマークにおいてSOTAな精度を達成している。またFixMatchがシンプルであることの利点としては必要なハイパーパラメータが少ないことがあげられる。そのため本論文では様々なablation studyを行うことができた。
FixMatch
FixMatchはconsistency regularizationとpseudo-labelingという2つの半教師あり学習のアプローチの組み合わせである(consistency regularizationにおいて弱いデータ拡張と強いデータ拡張を別々に使用している点も重要である)。
X = \{(x_b, p_b) : b \in (1,2,...,B)\} ,
U = \{u_b : b \in (1,2,...,\mu B)\}
$L$ クラス分類問題
バッチサイズ : $ B\ $
ラベルありデータ : $x_b$
one-hotラベル : $p_b$
ラベルなしデータ : $u_b$
XとUのデータセットサイズ比 : $\mu$
$p_m(y|x) \ $ : 入力$x$に対するモデル予測分布
$H(p, q)$ : 確率分布p,qのクロスエントロピー
$A(), \alpha()$ 強いデータ拡張、弱いデータ拡張
Background
consistency regularizationは最新の半教師あり学習アルゴリズムにおける重要な構成要素の一つである。具体的には同じ画像に摂動を与えてもモデルは同じように予測するはずであるという過程に依存して、ラベルなしデータを使用している。ラベルなしデータにおける損失関数は以下のようにあらわすことが出来る。このとき$\alpha, p_m$は確率的な関数であることに注意が必要。$\alpha$の代わりに敵対的な変換を使用したもの(VAT)、学習中の移動平均モデルの出力を用いたもの(Mean Teacher)などがある。
$$ \sum_{b=1}^{\mu B} ||p_m (y| \alpha(u_b)) - p_m (y|\alpha(u_b))||^2_2 $$
pseudo-labelingはラベルなしデータに対してモデルを用いて疑似ラベルを得るという考えを使用している。具体的にはモデルの出力のargmaxラベルを確信度が閾値を超えた場合のみ保持している。$q_b = p_m(y | u_b)$ $\hat{q_b} = argmax{q_b}$とするとpseudo-labelingの損失関数は以下の通りになる。pseudo-labelingはエントロピー最小化とも密接に関連している。
$$ \frac{1}{\mu B} \sum_{b=1}^{\mu B} 1 (max(q_b) \geq \tau) H(\hat{q_b}, q_b)$$
Our Algorithm: FixMatch
FixMatchの損失関数は教師あり損失$l_s\ $と教師なし損失$l_u\ $の項からなる。ラベルなしデータでは、弱いデータ拡張を施した画像のモデル予測 $q_b = p_m(y | \alpha(u_b))$ を計算し$\hat{q_b} = argmax q_b$を疑似ラベルとして、強いデータ拡張を施した画像のモデル出力とのクロスエントロピー誤差を用いて学習を行う。よって損失は次のように記述することが出来る。ただし$\tau$は閾値を意味するハイパーパラメータである。
l_s = \frac{1}{B} \sum_{b=1}^{B} H(p_b, p_m(\alpha(x_b))) ,
l_u = \frac{1}{\mu B} \sum_{b=1}^{\mu B} 1 (max(q_b) \geq \tau) H(\hat{q_b}, A(q_b)) \\
損失は $l_s + \lambda_u l_u$ によって定義される($\lambda_u$はハイパーパラメータ)。この損失はpseudo-labelingにおける損失と類似しているが、強いデータ拡張を施した画像から損失を計算しているという点で異なっていて、これによってconsistency regularizationを導入している。
また最新の半教師アルゴリズムでは学習中に$\lambda_u$を増加させることが一般的であるが、FixMatchでは不要である(学習初期は多くのデータが$max(q_b) \lt \tau$となり、学習が進むと$max(q_b) \gt \tau$ となるデータが増えるため = pseudo-labelingが自然なカリキュラムを"ただで"生成していると考えられる)。
Augmentation in FixMatch
FixMatchでは2種類のデータ拡張を活用している。弱いデータ拡張は50%のランダムフリップと最大12.5%のランダムシフトを用いている。強いデータ拡張ではAutoAugmentから派生した2つの手法(RandAugment, CTAugment)と、Cutoutを使用している。
Additional important factors
実験ではweight decay regularization(一般的なL2正則化)を使用, Adamでは性能が悪くなることが分かったためmomentumSGDを使用した。
Extensions of FixMatch
FixMatchはそのシンプルさ故に容易に拡張することが出来る。具体的にはReMixMatchで使用されているAugmentation Anchoring(M個の強いデータ拡張データを使用)やDistribution AlignmentなどをそのままFixMatchに適用することや、強いデータ拡張として敵対的摂動等を用いることも可能である。
Related work
自己学習(ラベルなしデータのモデルの予測を疑似ラベルとして学習すること)の考え方は古くからあり、NLPや物体検出、画像分類など多くの分野で使用されてきた。pseudo-labelingはモデル予測分布をhard labels(argmaxを取ったもの)に変換するものを指し、しばしば確信度の高いデータのみを保持するための閾値を用いて学習されている。いくつかの研究によってpseudo-labelingは他の半教師アルゴリズムと比較して精度が低いことが示唆されているが、pseudo-labelingはエントロピー最小化の一つの形態としてパイプラインの一部として使用されることが多い。
Consistency regularizationの初期の拡張ではモデルパラメータの指数移動平均(Mean Teacher)や敵対的摂動の利用(VAT)などが提案されていたが、近年では強いデータ拡張を用いることによって良い精度が得られることが分かっており、このような強いデータ拡張を施されたデータはデータ分布の外側にあるため半教師学習に有効であるという事が示されている。
FixMatchは既存研究のUDAとReMixMatchに類似している。両者とも弱いデータ拡張施した画像から疑似ラベルを生成し、強いデータ拡張を施した画像を用いてconsistencyを強制している。どちらもpseudo-labelingを使用しているわけではないが、代わりに予測ラベルを「シャープ」にするようなアプローチをとっている。FixMatchの閾値付き疑似ラベルはこのシャープ化と同様の効果を持っている。また、ReMixMatchはラベルなしデータの損失の重み$\lambda_u$をアニーリングしているが、FixMatchはこれを省略している(理由は前述)。シャープ化やアニーリングなどの複雑な要素を削除しつつ、pseudo-labelingとconsistency regularizationの技術を組み合わせていることからFixMatchはUDAやReMixMatchを単純化したものであるとみなすことが出来る。
consistency regularizationを含む半教師あり学習の比較。
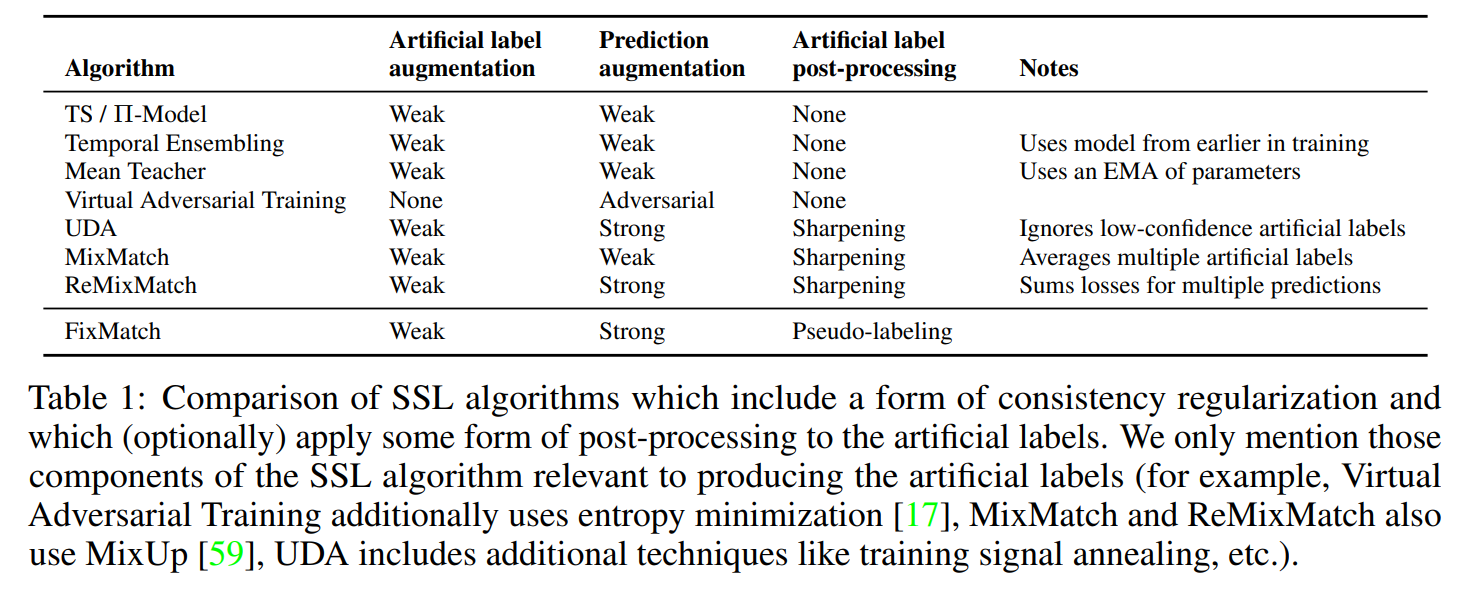
Experiments
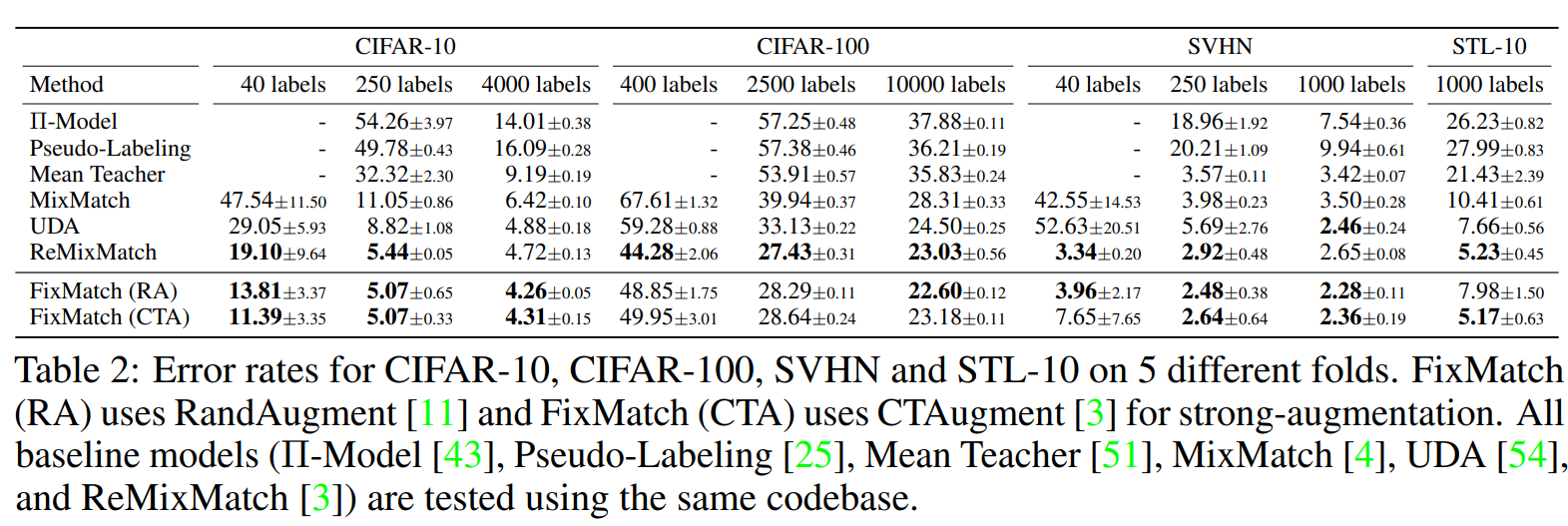
本実験では複数の半教師あり学習のベンチマーク(CIFAR-10/100, ImageNet等)を用いてFixMatchの有効性を評価する。結果として多くのデータセットで既存の手法を大幅に上回る制度を達成した。
CIFAR100においてはReMixMatchが最良の成績となっていたため、様々な要素をFixMatchに組み込み実験を行ったところ、Distribution Alignmentが重要なコンポーネントとなっていることを発見した。FixMatchとDAを組み合わせることでReMixMatchよりも高い精度を達成することが出来ている。
Ablation Study
実験の結果、閾値の代わりにシャープ化を用いた場合、ハイパーパラメータが導入される一方で精度の向上が確認されないという事が確認された。他にもデータ拡張におけるablation studyも行っている。
Conclusion
近年半教師あり学習は急速に進歩してきたが、複雑な構造が取り入れられてきた。我々は多くのデータセットに置いて最先端の精度を達成するよりシンプルな手法FixMatchを提案し、少ないラベルありデータからでも高精度を得ることが出来ることが確認できた。このような単純かつ性能の良い半教師アルゴリズムの存在がラベルを得ることが難しいドメインにおける機械学習の展開に役立つと信じている。
終わりに
過去に自己教師あり学習に関する論文を読んでいたので、近い分野の調査として半教師あり学習に関する研究について学んだ。半教師あり学習においても自己教師あり学習と同じくデータ拡張という概念が重要になっているのは面白いと感じた。あと自己教師あり学習と半教師あり学習の略称が同じSSLなのは良くないと思った。近い分野だから絶対分けた方がいいと思う。