Jupyter Notebookはプログラムを書きながら、途中途中で計算結果を確認できる便利なツールです。
またGoogle Colaboratoryを使うことで自分の環境に関わらず、計算できるのも利点です。
昨今話題のデータ解析の1つの手法として、位相的データ解析というものがあります。
これはデータを形として捉えて、その中に穴などの特徴がいくつあるか数える解析手法です。
始めに位相的と名前にあるように、位相幾何学(Topology)について説明します。
Topologyとは?
wikipediaでは「トポロジーは、何らかの形(かたち。あるいは「空間」)を連続変形(伸ばしたり曲げたりすることはするが切ったり貼ったりはしないこと)しても保たれる性質(位相的性質または位相不変量)に焦点を当てたものである。」とされている。
Topologyを説明する際によく用いられる、「コーヒーカップ」と「ドーナツ」がTopology的な視点で見ると同じというの聞いた人も多いと思います。
wikipedea 位相幾何学より引用
この図から、「コーヒーカップ」と「ドーナツ」を切り貼りせずに曲げ伸ばしすることで変形可能なことがわかります。
これは穴の数という位相的不変量が1つという共通点が同じであることを表しています。
今回の記事では、2次元図形の中の穴の数を数えるHomologyの計算を行いました。
Homologyの計算手順
ホモロジーの具体的な計算は、
入力:データの座標,データの半径
出力:データの中の穴の数
として行います。
データを入力
計算したいデータを入力します。今回はランダムに作成したデータを用いて計算を行いました。
import os
import random as rd
import numpy as np
import copy
# ポイントクラウドデータ作成
# データ次元
dim = 2
# データ数
data_size = 500
# 複体半径
sim_r = 0.08
def make_point_cloud(dim,size):
arr = np.random.rand(size, dim).astype(np.float64)
return arr
data = make_point_cloud(dim,data_size)
次に穴の数を計算するために、データがつながった連結体を計算する。
連結体の計算
データはただの座用であるため、データに半径を与えた図を次に示す。

def distance(data1,data2):
r = data1 - data2;
r = np.sqrt(np.sum(np.power(r,2.0)))
return r
def make_path_matrix(data,r):
size ,data_dim = data.shape
path_matrix = [[0 for j in range(size)]for i in range(size)]
for i in range(size):
for j in range(size):
if distance(data[i],data[j]) <= 2*r:
path_matrix[i][j] = 1;
return path_matrix
# 隣接行列を作成
pathM = make_path_matrix(data,sim_r)
# detaの到達フラグ 未到達:0 到達:1
flaglist = [0 for i in range(data_size)]
# 隣接行列を再帰的に探索する関数
def visit(i,path):
flaglist[i] = 1
for j in range(data_size):
if(path[i][j] == 1 and flaglist[j] == 0):
visit(j,path)
# 連結体
K = []
for i in range(data_size):
#連結体の1つを保存
comp = [];
#探索前のflaglistを保存
flaglistsave = copy.deepcopy(flaglist);
#探索済みかの確認
if flaglist[i] == 0:
#未探索の際に探索
visit(i,pathM);
#探索フラグリストを確認
for flagindex in range(data_size):
#探索済みかつ新たに探索された点を確認
if flaglist[flagindex] == 1 and flaglistsave[flagindex] == 0:
#連結体に追加
comp.append(flagindex);
#連結体の集合に追加
K.append(comp);
データに半径を持たせることで、円がつながっている連結体に分けられることがわかる。
次に連結体の中に含まれる最小単位の単体について調べる。
単体の作成
単体とは連結体を構成する最小単位であり、単体とは点や線、面などがそれに当たります。
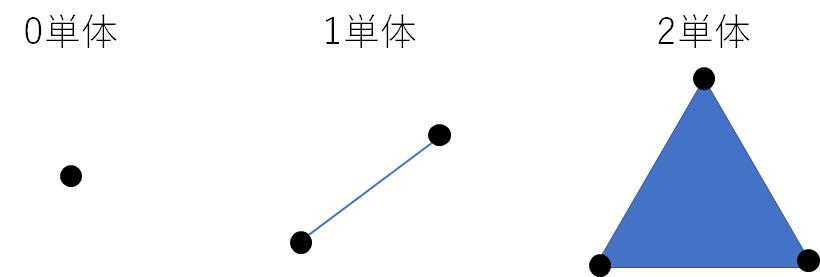
点だけの時を0単体と呼び、線を1単体、三角形の面を2単体と呼びます。
今回は2次元の穴を数えるため2単体までですが、三次元では四面体が3単体となりより高い次元でも定義されます。
2単体の構成では下の図のように、三角形の各片が1単体を構成していても2単体を構成しないときが存在します。
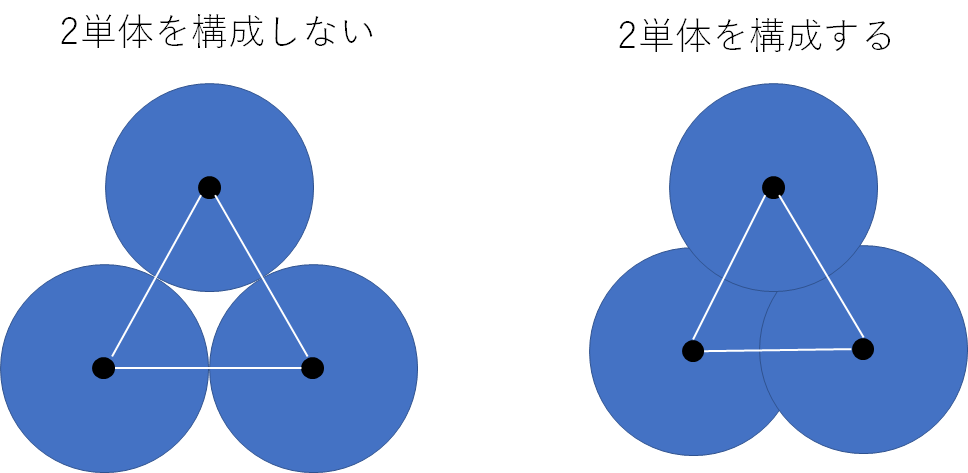
計算速度の速いアルファ複体を用いるられるようですが、分からないのでチェック複体で計算しました
# 2単体の構成を確認 改善
def checksim2(point,r):
a = point[0];
b = point[1];
c = point[2];
da = distance(b,c)
db = distance(a,c)
dc = distance(b,a)
#3辺がそれぞれ1単体を構成するか確認
sim1flag = da <(2*r) and db<(2*r) and dc<(2*r)
#ヘロンの公式
ss = (da + db + dc)/2
#print(ss * (ss - da)*(ss - db)*(ss - dc))
S = np.sqrt(ss * (ss - da)*(ss - db)*(ss - dc))
MaxS = np.power(r,2) * np.sin(np.pi/6)*np.cos(np.pi/6)/2*3
#面積確認
Sflag = S<MaxS
#外接円判定
cosC = (np.power(da,2) + np.power(db,2) - np.power(dc,2))/(2*da*db)
sinC =np.sqrt(1 - np.power(cosC,2))
outerflag = 2*sinC*sim_r > dc
if (Sflag and sim1flag) or (outerflag and sim1flag):
return 1
else:
return 0
# 連結体の個数
betti0 = len(K)
# 1単体のリスト
sim1list = [[] for i in range(betti0)]
# 2単体のリスト
sim2list = [[] for i in range(betti0)]
# 1単体と2単体が一つのみの連結体を抽出
for i in range(betti0):
if len(K[i]) <4 and len(K[i]) != 1:
if len(K[i]) == 2:
sim1list[i] = copy.deepcopy([K[i]])
if len(K[i]) == 3 and checksim2([data[K[i][0]],data[K[i][1]],data[K[i][2]]],sim_r) == 1:
sim2list[i] = copy.deepcopy([K[i]])
# 連結体から、1単体を抽出
for b in range(betti0):
if len(K[b]) > 2:
for i in range(1,len(K[b]),1):
for j in range(0,i,1):
if pathM[K[b][i]][K[b][j]] == 1:
sim1list[b].append([K[b][i],K[b][j]])
# 連結体から、2単体を抽出
for b in range(betti0):
if len(K[b]) > 3:
for i in range(2,len(K[b]),1):
for j in range(1,i,1):
for k in range(0,j,1):
l = [data[K[b][i]],data[K[b][j]],data[K[b][k]]]
if checksim2(l,sim_r) == 1:
sim2list[b].append([K[b][i],K[b][j],K[b][k]])
連結体の中の単体を数えることで、有限個の単体が入った集合を作成する。
次に単体を別の次元の単体に変換する写像、境界写像を説明する。
境界写像
境界写像とは、単体を一つ次元の小さい単体に変換する写像である。
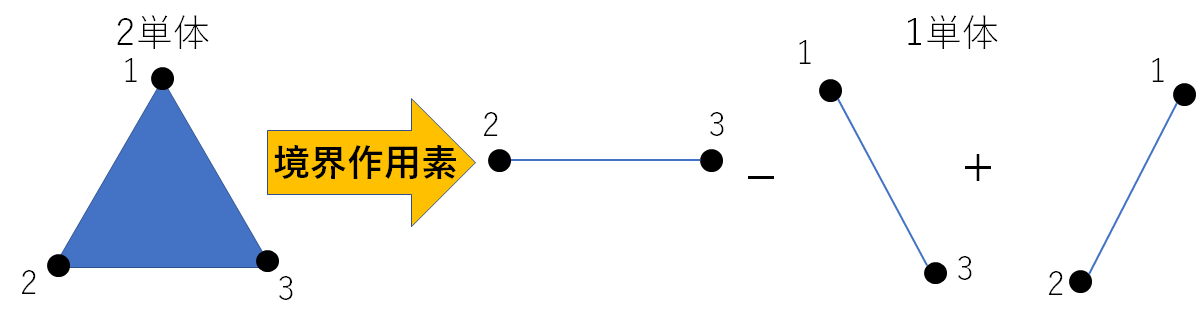
図のように2単体から、1単体の交代和に変換する写像となっている。
具体的な写像は次のようになり
\langle 1,2,3 \rangle = \langle 2,3 \rangle - \langle 1,3 \rangle + \langle 1,2 \rangle
元の単体から除いた番号が前から何番目を偶数奇数で符号を変えて和をとる写像となっている。
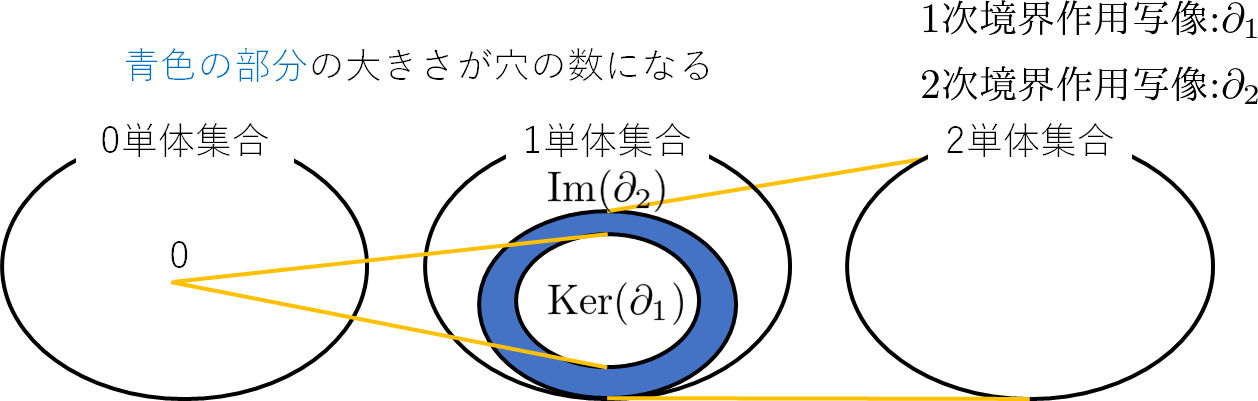
連結体に含まれる2単体から1単体に移す境界写像を2次境界写像、1単体から0単体に移す境界写像を1次境界写像という。
この得られた2次境界写像と1次境界写像を表現行列として表す。
次にこの境界作用素から、穴の数を数える計算を説明する。
# 連結体と1単体、2単体をソート
cmp = [sorted(l, reverse=True) for l in K]
K = copy.deepcopy(cmp)
del cmp
cmp = [[ sorted(s, reverse=True) for s in l]for l in sim1list]
sim1list = copy.deepcopy(cmp)
del cmp
cmp = [[ sorted(s, reverse=True) for s in l]for l in sim2list]
sim2list = copy.deepcopy(cmp)
del cmp
# 1次境界作用素
boundary1 = [[] for _ in range(betti0)]
for b in range(betti0):
if len(sim1list[b]) > 0:
M = np.ones((len(K[b]),len(sim1list[b])),dtype=np.int8)
for i in range(len(K[b])):
for j in range(len(sim1list[b])):
if len(K[b]) > 1:
if sim1list[b][j][0] == K[b][i]:
M[i][j] = 1
else:
if sim1list[b][j][1] == K[b][i]:
M[i][j] = -1
else:
M[i][j] = 0
else:
if sim1list[b][j][0] == K[b]:
M[i][j] = 1
else:
if sim1list[b][j][1] == K[b]:
M[i][j] = -1
else:
M[i][j] = 0
boundary1[b] = copy.deepcopy(M)
boundary2 = [[] for _ in range(betti0)]
for b in range(betti0):
if len(sim2list[b]) > 0:
M = np.ones((len(sim1list[b]),len(sim2list[b])),dtype=np.int8)
for i in range(len(sim1list[b])):
for j in range(len(sim2list[b])):
if [sim2list[b][j][1],sim2list[b][j][2]] == sim1list[b][i]:
M[i][j] = 1
else:
if [sim2list[b][j][0],sim2list[b][j][2]] == sim1list[b][i]:
M[i][j] = -1
else:
if [sim2list[b][j][0],sim2list[b][j][1]] == sim1list[b][i]:
M[i][j] = 1
else:
M[i][j] = 0
boundary2[b] = copy.deepcopy(M)
穴の数を数える
データの中の穴の数は次の図の領域になります。
2次境界写像$\partial_2$の像と1次境界写像$\partial_1$の核がそれぞれが可換群なっており,その商群の次元から穴の数が得られるらしい。
厳密なことまで分からないので、今回計算した式を次に示す。
B_1 = dim(Ker(\partial_1)) - dim(Im(\partial_2))\\
B_1 = (dim(C_1) - rank(\partial_1)) - rank(\partial_2)
$dim(C_1)$は連結体に含まれる1単体の数
# 1次ベッチ数を数える変数
betti1 = 0
for b in range(betti0):
rank1 = 0
rank2 = 0
#1次境界作用素の有無の確認
if len(boundary1[b]) != 0:
rank1 = GPU_rank(boundary1[b])
if len(boundary2[b]) != 0:
rank2 = GPU_rank(boundary2[b])
betti1 += len(sim1list[b]) - rank1 - rank2
print("連結体の番号",b," ",len(sim1list[b]),"-",rank1,"-",rank2,"=",len(sim1list[b]) - rank1 - rank2)
print("1次ベッチ数は、",betti1,"となる")
計算結果
データを可視化すると

となり、図形の中に白い穴が5つあることがわかる。
またこのデータで、Homology計算プログラムを行った結果
連結体の番号 0 414 - 99 - 310 = 5
1次ベッチ数は、 5 となる
という結果が得られ、穴の数を数えられたことがわかります。
データの可視化
データの可視化はProcessingを利用しました。そのプログラムがこちらになります。
String lin;
String linR;
int ln;
static final int img_size = 800;
float r;
String lines[];
String linesR[];
void setup() {
ln = 0;
//r = 0.1;
lines = loadStrings("pointcloud.csv");
linesR = loadStrings("r.csv");
linR = linesR[0];//ln行目を収納
String [] coR = split(linR,',');
if (coR.length == 1){
r = float(coR[0]);
}
//txtファイルの読み込み
background(#FFFFFF);
size(1000,1000);
println(r);
for(ln = 0;ln < lines.length;ln++){
lin = lines[ln];//ln行目を収納
String [] co = split(lin,',');
if (co.length == 2){
float x = float(co[0]);
float y = float(co[1]);
fill(#000000);
noStroke();
ellipse(x*img_size + 100,
1000 -(y*img_size + 100),
2*r*img_size,
2*r*img_size);
}
}
}
void draw() {
}
座標データをpointcloud.csv、半径の値をr.csvとして保存してください。
参考にさせていただいたページ
https://cookie-box.hatenablog.com/entry/2016/12/04/132021
http://peng225.hatenablog.com/entry/2017/02/05/235951
http://peng225.hatenablog.com/entry/2017/02/18/133838
最後に
複体を構成する部分など、計算時間が長くなってしまっているので短縮する方法を調べていきたいです。
位相的データ解析としてパーシステントホモロジーが有名です。もともとそちらを各つもりでしたが、具体的なプログラムを書くことができずHomologyのプログラムを書きました。
もしこの記事を読んだ方で、アルファ複体や行列のランク計算の高速化、パーシステントホモロジーの計算など教えていただけたら幸いです。