概要
有限要素法でせん断ロッキングを防ぐ手段として使われる非適合要素をPythonで実装してみます。
この記事では、一番代表的と思われるWilson-Taylorの非適合要素(QM6)を実装しています。
Wilson-Taylorの非適合要素は2次元では4節点の四角形要素となります。
前提知識
・四角形要素の要素剛性マトリクスの式
有限要素法の定式化 アイソパラメトリック要素
FEM要約(四角形)
・仮想仕事の原理
仮想仕事の原理
・ガウス求積
非適合要素とは
非適合要素は要素を曲げ変形させた時に発生するせん断ロッキングを解決するために使用される要素です。せん断ロッキングは下の図のように曲げ変形して欲しい要素が実際には台形のように変形することによって起きる現象で四角形要素のような要素内の変位が1次式で表される要素に対して起こります。この現象が起きるとせん断ひずみにエネルギーを消費するため、剛性が実際より大きい結果となります。
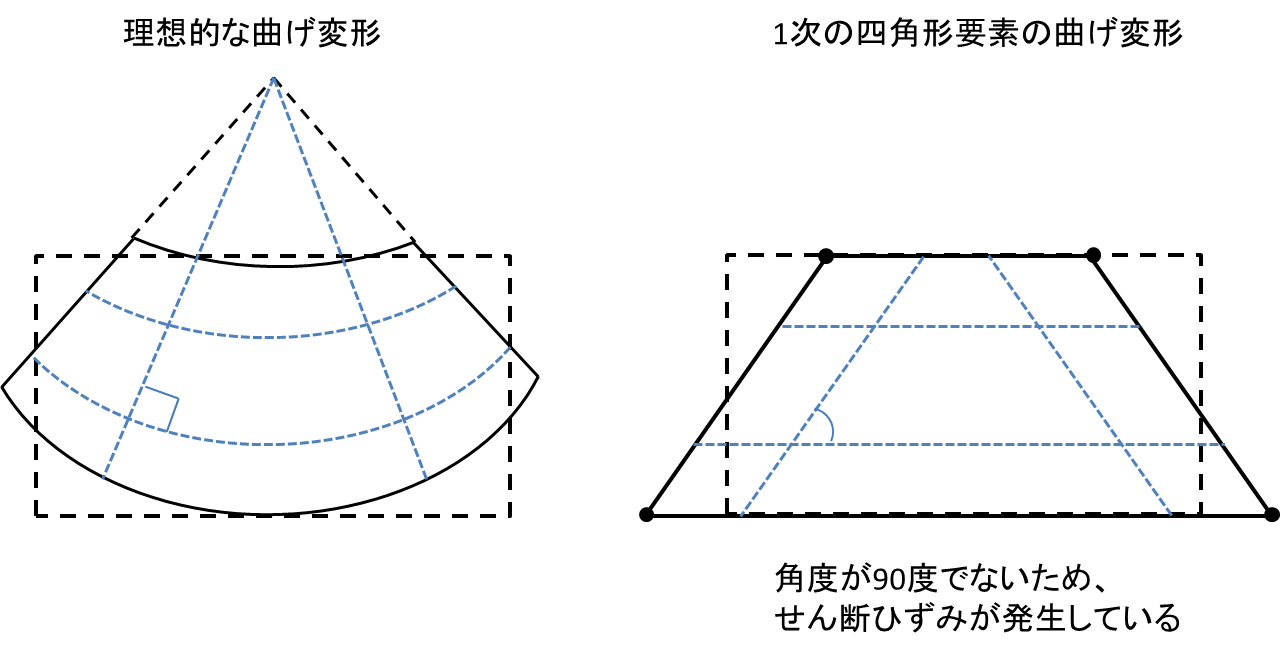
そこで、変位を2次式で表される2次要素を使えば良いわけですが、2次要素は節点数が倍になり、モデル作成に手間がかかりますし、1次要素と比較して計算時間も増大します。
そこで、なんとか1次要素のまま曲げの変形も再現できるように工夫したのが非適合要素です。
Wilson-Taylorの非適合要素では四角形要素の変位に下記のように変数$\alpha_i$を追加して曲げも再現できるようにしています。
u(a,b) = \sum_{i=1}^4 N_i(a,b) u_i + \alpha_1(1-a^2) + \alpha_2(1-b^2) \\
v(a,b) = \sum_{i=1}^4 N_i(a,b) v_i + \alpha_3(1-a^2) + \alpha_4(1-b^2) \\
u : x方向の変位 \\
v : y方向の変位 \\
N_i : 四角形要素の形状関数 \\
u_i : i節点のx方向の変位 \\
v_i : i節点のy方向の変位 \\
\alpha_i : 新たに追加する変数
このようにすることで下記の図のように変形することが可能となります。

ここで、新しく追加した$\alpha_i$は要素毎に独立した値として持つため、他の要素との繋がりは考慮していません。そのため、要素辺での変位量は下の図のように隣り合う要素と一致しなくなります。

要素辺で変位が適合しないので、非適合要素と呼ばれています。
非適合要素の定式化
非適合要素では要素の変位を下記の式に置き換えます。
\boldsymbol{u} = \boldsymbol{N}\boldsymbol{u}_e + \boldsymbol{P} \boldsymbol{\alpha} \\
\boldsymbol{N} =
\begin{bmatrix}
N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4 & 0 \\
0 & N_1 & 0 & N_2 & 0 & N_3 & 0 & N_4
\end{bmatrix}
\\
\boldsymbol{u}_e =
\begin{bmatrix}
u_1 \\
v_1 \\
u_2 \\
v_2 \\
u_3 \\
v_3 \\
u_4 \\
v_4 \\
\end{bmatrix}
\\
\boldsymbol{P} =
\begin{bmatrix}
1 - a^2 & 1 - b^2 & 0 & 0\\
0 & 0 & 1 - a^2 & 1 - b^2
\end{bmatrix}
\\
\boldsymbol{\alpha} =
\begin{bmatrix}
\alpha_1 \\
\alpha_2 \\
\alpha_3 \\
\alpha_4
\end{bmatrix}
\\
\begin{align}
&N_1 = \frac{1}{4}(1-a)(1-b) & &N_2 = \frac{1}{4}(1+a)(1-b) \\
&N_3 = \frac{1}{4}(1+a)(1+b) & &N_4 = \frac{1}{4}(1-a)(1+b)
\end{align}
すると、要素内のひずみ$\boldsymbol{\epsilon}$は偏微分により、下記の式で表せます。
\boldsymbol{\epsilon} =
\begin{bmatrix}
\epsilon_x \\
\epsilon_y \\
\gamma_{xy}
\end{bmatrix}
=
\begin{bmatrix}
\frac{\partial u}{\partial x} \\
\frac{\partial v}{\partial y} \\
\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}
\end{bmatrix}
=
\boldsymbol{B}_c \boldsymbol{u}_e + \boldsymbol{B}_I \boldsymbol{\alpha} \\
\boldsymbol{B}_c =
\begin{bmatrix}
\frac{\partial N_1}{\partial x} && 0 && \frac{\partial N_2}{\partial x} && 0 && \frac{\partial N_3}{\partial x} && 0 && \frac{\partial N_4}{\partial x} && 0 \\
0 && \frac{\partial N_1}{\partial y} && 0 && \frac{\partial N_2}{\partial y} && 0 && \frac{\partial N_3}{\partial y} && 0 && \frac{\partial N_4}{\partial y} \\
\frac{\partial N_1}{\partial y} && \frac{\partial N_1}{\partial x} &&
\frac{\partial N_2}{\partial y} && \frac{\partial N_2}{\partial x} &&
\frac{\partial N_3}{\partial y} && \frac{\partial N_3}{\partial x} &&
\frac{\partial N_4}{\partial y} && \frac{\partial N_4}{\partial x}
\end{bmatrix}
\\
\boldsymbol{B}_I =
\begin{bmatrix}
-2a\frac{\partial a}{\partial x} && -2b\frac{\partial b}{\partial x} && 0 && 0 \\
0 && 0 && -2a\frac{\partial a}{\partial y} && -2b\frac{\partial b}{\partial y} \\
-2a\frac{\partial a}{\partial y} && -2b\frac{\partial b}{\partial y} && -2a\frac{\partial a}{\partial x} && -2b\frac{\partial b}{\partial x}
\end{bmatrix}
$\boldsymbol{B}_c$マトリクスは四角形要素の$\boldsymbol{B}$マトリクスになります。
ここで、要素内のひずみ$\boldsymbol{\epsilon}$と変位$\boldsymbol{u}$を下記のように行列形式で書き換えると
\boldsymbol{\epsilon} =
\begin{bmatrix}
\boldsymbol{B}_c && \boldsymbol{B}_I \\
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix}
\\
\boldsymbol{u} =
\begin{bmatrix}
\boldsymbol{N} && \boldsymbol{P} \\
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix}
となり、応力ベクトル$\boldsymbol{\sigma}$は下記の式で表せます。
\boldsymbol{\sigma}=
\boldsymbol{D}\boldsymbol{\epsilon} =
\boldsymbol{D}
\begin{bmatrix}
\boldsymbol{B}_c && \boldsymbol{B}_I \\
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix}
\\
\boldsymbol{D} : 応力-ひずみマトリクス
ここで要素内で仮想仕事の原理を考えてみます。仮想仕事の原理は下記の式で与えられます。
\int_v \delta \boldsymbol{\epsilon}^T \boldsymbol{\sigma} dV =
\int_v \delta \boldsymbol{u}^T \boldsymbol{b} dV + \int_s \delta \boldsymbol{u}^T \boldsymbol{t} dS \\ \\
\delta \boldsymbol{\epsilon} : 要素内の仮想ひずみ \\
\delta \boldsymbol{u} : 要素内の仮想変位 \\
\boldsymbol{b} : 物体力 \\
\boldsymbol{t} : 表面力 \\
上の式にこれまでの不適合要素の式を代入すると下記のように表せます。
\int_v
(
\begin{bmatrix}
\boldsymbol{B}_c && \boldsymbol{B}_I \\
\end{bmatrix}
\begin{bmatrix}
\delta \boldsymbol{u}_e \\
\delta \boldsymbol{\alpha} \\
\end{bmatrix}
)^T
\boldsymbol{D}
\begin{bmatrix}
\boldsymbol{B}_c && \boldsymbol{B}_I \\
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix} dV =
\int_v
(
\begin{bmatrix}
\boldsymbol{N} && \boldsymbol{P} \\
\end{bmatrix}
\begin{bmatrix}
\delta \boldsymbol{u}_e \\
\delta \boldsymbol{\alpha} \\
\end{bmatrix}
)^T
\boldsymbol{b} dV + \int_s
(
\begin{bmatrix}
\boldsymbol{N} && \boldsymbol{P} \\
\end{bmatrix}
\begin{bmatrix}
\delta \boldsymbol{u}_e \\
\delta \boldsymbol{\alpha} \\
\end{bmatrix}
)^T
\boldsymbol{t} dS \\
\begin{bmatrix}
\delta \boldsymbol{u}_e \\
\delta \boldsymbol{\alpha} \\
\end{bmatrix} ^T
\int_v
\begin{bmatrix}
\boldsymbol{B}_c^T \\
\boldsymbol{B}_I^T \\
\end{bmatrix}
\boldsymbol{D}
\begin{bmatrix}
\boldsymbol{B}_c && \boldsymbol{B}_I \\
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix}
dV
=
\begin{bmatrix}
\delta \boldsymbol{u}_e \\
\delta \boldsymbol{\alpha} \\
\end{bmatrix} ^T
\int_v
\begin{bmatrix}
\boldsymbol{N}^T \\
\boldsymbol{P}^T
\end{bmatrix}
\boldsymbol{b}
dV
+
\begin{bmatrix}
\delta \boldsymbol{u}_e \\
\delta \boldsymbol{\alpha} \\
\end{bmatrix} ^T
\int_s
\begin{bmatrix}
\boldsymbol{N}^T \\
\boldsymbol{P}^T
\end{bmatrix}
\boldsymbol{t}
dS
\\
\int_v
\begin{bmatrix}
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_c &&
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_I \\
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{B}_c &&
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{B}_I \\
\end{bmatrix}
dV
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix}
=
\int_v
\begin{bmatrix}
\boldsymbol{N}^T \\
\boldsymbol{P}^T
\end{bmatrix}
\boldsymbol{b}
dV
+
\int_s
\begin{bmatrix}
\boldsymbol{N}^T \\
\boldsymbol{P}^T
\end{bmatrix}
\boldsymbol{t}
dS
\\
ここで下記のように式を置き換えます。
\boldsymbol{K}
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix}
=
\begin{bmatrix}
\boldsymbol{f}_e \\
\boldsymbol{f}_{\alpha} \\
\end{bmatrix}
\\
\boldsymbol{K}=
\int_v
\begin{bmatrix}
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_c &&
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_I \\
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{B}_c &&
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{B}_I \\
\end{bmatrix}
dV
\\
\boldsymbol{f}_e : 要素節点の等価節点力 \\
\boldsymbol{f}_{\alpha} : \boldsymbol{\alpha}による内力
上の式では仮想仕事の原理の物体力、表面力の項を$\boldsymbol{f}_e$、$\boldsymbol{f}_{\alpha}$で置き換えています。
ここで、$\boldsymbol{f}_{\alpha}$が内力として発生していますが、Wilson-Taylorの非適合要素では$\boldsymbol{f}_{\alpha}=\boldsymbol{0}$と仮定して解きます。
上記の仮定を踏まえて式を整理すると下記のように表せます。
\begin{bmatrix}
\boldsymbol{K}_{cc} && \boldsymbol{K}_{cI} \\
\boldsymbol{K}_{Ic} && \boldsymbol{K}_{II}
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{u}_e \\
\boldsymbol{\alpha} \\
\end{bmatrix}
=
\begin{bmatrix}
\boldsymbol{f}_e \\
\boldsymbol{0} \\
\end{bmatrix}
\\
\boldsymbol{K}_{cc}=
\int_v
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_c
dV
\\
\boldsymbol{K}_{cI} = \boldsymbol{K}_{Ic}^T =
\int_v
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_I
dV
\\
\boldsymbol{K}_{II} =
\int_v
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{B}_I
dV
上の式では$\boldsymbol{\alpha}$という値が含まれていますが、式を変形することで$\boldsymbol{\alpha}$を消すことが可能です。
\left\{
\begin{array}{ll}
\boldsymbol{K}_{cc} \boldsymbol{u}_e + \boldsymbol{K}_{cI} \boldsymbol{\alpha} = \boldsymbol{f}_e \\
\boldsymbol{K}_{Ic} \boldsymbol{u}_e + \boldsymbol{K}_{II} \boldsymbol{\alpha} = \boldsymbol{0} \\
\end{array}
\right.
\\
\quad
\\
\boldsymbol{\alpha} = -\boldsymbol{K}_{II}^{-1} \boldsymbol{K}_{Ic} \boldsymbol{u}_e \\
\boldsymbol{K}_{cc} \boldsymbol{u}_e - \boldsymbol{K}_{cI} \boldsymbol{K}_{II}^{-1} \boldsymbol{K}_{Ic} \boldsymbol{u}_e = \boldsymbol{f}_e \\
\\
\quad
\\
\boldsymbol{K}_e \boldsymbol{u}_e = \boldsymbol{f}_e \\
\boldsymbol{K}_e = \boldsymbol{K}_{cc} - \boldsymbol{K}_{cI} \boldsymbol{K}_{II}^{-1} \boldsymbol{K}_{Ic}
上記の処理は静的縮約と呼ばれ、この操作により要素剛性マトリクス$K_e$を求めることができます。
また、要素剛性マトリクス$K_e$はガウス求積を使って下記のように計算することが可能です。
\boldsymbol{K}_{cc}=
\int_v
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_c
dV
=
t \sum_{i=1}^2 \sum_{j=1}^2 w_i w_j \boldsymbol{B}_c^T(a_i, b_i) \boldsymbol{D} \boldsymbol{B}_c(a_i, b_i) |\boldsymbol{J}(a_i,b_i)| \\
\boldsymbol{K}_{cI} = \boldsymbol{K}_{Ic}^T =
\int_v
\boldsymbol{B}_c^T \boldsymbol{D} \boldsymbol{B}_I dV
= t \sum_{i=1}^2 \sum_{j=1}^2 w_i w_j \boldsymbol{B}_c^T(a_i, b_i) \boldsymbol{D} \boldsymbol{B}_I(a_i, b_i) |\boldsymbol{J}(a_i,b_i)|
\\
\boldsymbol{K}_{II} =
\int_v
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{B}_I
dV
=
t \sum_{i=1}^2 \sum_{j=1}^2 w_i w_j \boldsymbol{B}_I^T(a_i, b_i) \boldsymbol{D} \boldsymbol{B}_I(a_i, b_i) |\boldsymbol{J}(a_i,b_i)|
\\
t : 要素の厚さ \\
w_i : 積分点の重み係数 \\
|\boldsymbol{J}| : x,y座標系からa,b座標系に変数変換するためのヤコビアン \\
積分点の位置と重み係数
|$i$ |$j$ |$w_i$ |$w_j$ |$a_i$ |$b_j$ |
|---|---|---|---|---|---|---|
|1 |1 |1.0 |1.0 |$-\frac{1}{\sqrt{3}}$ |$-\frac{1}{\sqrt{3}}$ |
|1 |2 |1.0 |1.0 |$\frac{1}{\sqrt{3}}$ |$-\frac{1}{\sqrt{3}}$ |
|2 |1 |1.0 |1.0 |$\frac{1}{\sqrt{3}}$ |$\frac{1}{\sqrt{3}}$ |
|2 |2 |1.0 |1.0 |$-\frac{1}{\sqrt{3}}$ |$\frac{1}{\sqrt{3}}$ |
ヤコビ行列$\boldsymbol{J}$の導出に関しては前提知識の項目をご参照ください。
また、要素の節点変位ベクトル$\boldsymbol{u}_e$を求めた後に、要素のひずみベクトル$\boldsymbol{\epsilon}$、応力ベクトル$\boldsymbol{\sigma}$は下記の式で求めることが可能です。
\boldsymbol{\epsilon}
=
\boldsymbol{B}_c \boldsymbol{u}_e + \boldsymbol{B}_I \boldsymbol{\alpha}
=
\boldsymbol{B}_c \boldsymbol{u}_e - \boldsymbol{B}_I \boldsymbol{K}_{II}^{-1} \boldsymbol{K}_{Ic} \boldsymbol{u}_e
\\
\boldsymbol{\sigma}= \boldsymbol{D}\boldsymbol{\epsilon}
さて、上記の式を用いることで解析ができるようになったわけですが、このままではパッチテストを通過することができないという問題があります。
パッチテストは要素の品質を計る一つの指標で、要素内で定ひずみ(定応力)状態を再現することができるかが問われます。定ひずみ状態を再現することができれば要素を細かく分割するほど精度が高くなる(収束性)ことが保証されます。
ここで、非適合要素と四角形要素のひずみを比較してみます。
非適合要素 : \boldsymbol{\epsilon} = \boldsymbol{B}_c \boldsymbol{u}_e + \boldsymbol{B}_I \boldsymbol{\alpha} \\
四角形要素 : \boldsymbol{\epsilon} = \boldsymbol{B}_c \boldsymbol{u}_e
四角形要素と比較して$\boldsymbol{\alpha}$の項が追加されていることが分かります。そして、四角形要素は定ひずみ(定応力)状態を再現できることが分かっています。なので、$\boldsymbol{\alpha} = \boldsymbol{0}$となれば、定ひずみ(定応力)状態を再現することができるはずです。そこで、$\boldsymbol{\alpha}$の式を振り返ってみると、
\boldsymbol{\alpha} = - \boldsymbol{K}_{II}^{-1} \boldsymbol{K}_{Ic} \boldsymbol{u}_e
となっていました。ここで、定ひずみ状態の変位を$\boldsymbol{u}_e = \boldsymbol{u}_l$として
式に代入すると、
\begin{align}
\boldsymbol{\epsilon}_c &= \boldsymbol{B}_c \boldsymbol{u}_l = const \\
\boldsymbol{\alpha} &=
-\boldsymbol{K}_{II}^{-1} \boldsymbol{K}_{Ic} \boldsymbol{u}_l
\\
&=
-\boldsymbol{K}_{II}^{-1} \int_v
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{B}_c \boldsymbol{u}_l dV
\\
&= -\boldsymbol{K}_{II}^{-1} \int_v
\boldsymbol{B}_I^T \boldsymbol{D} \boldsymbol{\epsilon}_{c}
dV
\\
&= -\boldsymbol{K}_{II}^{-1} \boldsymbol{D} \boldsymbol{\epsilon}_c \int_v
\boldsymbol{B}_I^T dV
\end{align}
\\
\boldsymbol{\epsilon}_{c} : 定ひずみ
となるので、
\int_v
\boldsymbol{B}_I^T dV = \boldsymbol{0}
となれば$\boldsymbol{\alpha} = \boldsymbol{0}$となることが分かります。
ところが、$\boldsymbol{B}_I$は要素の初期の形状にのみ依存する値なので、
定ひずみ状態の変位$\boldsymbol{u}_l$が与えられても、$\boldsymbol{\alpha} = \boldsymbol{0}$になるとは限らないことが分かります。
そこで、定ひずみ状態のときに必ず$\boldsymbol{\alpha} = \boldsymbol{0}$となるように$\boldsymbol{B}_I$を補正します。
これまで使用してきた$\boldsymbol{B}_I$を$\bar{\boldsymbol{B}}_I$として下記の式で置き換えます。
\bar{\boldsymbol{B}}_I = \boldsymbol{B}_I + \boldsymbol{B}_{IC}
\\
\boldsymbol{B}_{IC} : \boldsymbol{B}_Iの補正項
ここで、$\boldsymbol{B}_{IC}$は要素内で一定値とします。
この式を使って、定ひずみのときに$\boldsymbol{\alpha}=\boldsymbol{0}$とすると、
\int_v \bar{\boldsymbol{B}_I}^T dV =
\int_v (\boldsymbol{B}_I + \boldsymbol{B}_{IC})^T dV =
\int_v \boldsymbol{B}_I^T dV + V \boldsymbol{B}_{IC}^T= \boldsymbol{0}
\\
\boldsymbol{B}_{IC} = -\frac{\int_v \boldsymbol{B}_I dV}{V}
\\
V : 要素の体積
となり$\boldsymbol{B}_{IC}$を求めることが可能となります。これにより、これまでの式の$\boldsymbol{B_I}$を$\bar{\boldsymbol{B_I}}$に置き換えることで、定ひずみ状態の再現が可能となります。
Pythonで非適合要素を実装する
クラスの構成
Pythonで実装するために以下のようなクラスを実装します。
- Node2dクラス(Node2d.py) :
節点情報を格納するためのクラス - Dmatrix2dクラス(Dmatrix2d.py) :
Dマトリクスを計算するためのクラス - d2cps4iクラス(d2cps4i.py) :
平面応力状態の4節点不適合要素の各種計算をするためのクラス - Boundary2dクラス(Boundary2d.py) :
境界条件を格納するためのクラス - FEM2dクラス(FEM2d.py) :
有限要素法の解析を行うクラス
Node2dクラス
節点の情報を格納するだけのクラスです
Node2d.py
class Node2d:
# コンストラクタ
# no : 節点番号
# x : x座標
# y : y座標
def __init__(self, no, x, y):
self.no = no # 節点番号
self.x = x # x座標
self.y = y # y座標
# 節点の情報を表示する
def printNode(self):
print("Node No: %d, x: %f, y: %f" % (self.no, self.x, self.y))
Dmatrix2dクラス
Dマトリクスを計算するためのクラスです。
平面応力状態と平面ひずみ状態に対応しています。
Dmatrix2d.py
import numpy as np
class Dmatrix2d:
# コンストラクタ
# young : ヤング率
# poisson : ポアソン比
def __init__(self, young, poisson):
self.young = young
self.poisson = poisson
# 平面応力状態のDマトリクスを作成する
def makeDcpsmatrix(self):
coef = self.young / (1 - self.poisson * self.poisson)
matD = np.matrix([[1.0, self.poisson, 0.0],
[self.poisson, 1.0, 0.0],
[0.0, 0.0, 0.5 * (1 - self.poisson)]])
matD *= coef
return matD
# 平面ひずみ状態のDマトリクスを作成する
def makeDcpematrix(self):
coef = self.young / ((1.0 - 2 * self.poisson) * (1.0 + self.poisson))
matD = np.matrix([[1.0 - self.poisson, self.poisson, 0.0],
[self.poisson, 1.0 - self.poisson, 0.0],
[0.0, 0.0, 0.5 * (1 - 2 * self.poisson)]])
matD *= coef
return matD
d2cps4iクラス
平面応力状態の4節点不適合要素のクラスで、要素剛性マトリクス、応力、ひずみの計算が可能です。
makeOutputData関数は解析により要素の変位が求まった後に使う関数で、要素の変位から応力、ひずみ、ミーゼス応力を計算して返します。
ヤコビ行列$\boldsymbol{J}$と$\boldsymbol{B}_c$、$\boldsymbol{B}_I$マトリクスはガウス求積で使うために積分点の位置で求めてリスト化しています。
なお、平面ひずみ状態はDマトリクスを平面ひずみのものに変えるだけで実装できます。
d2cps4i.py
import numpy as np
import numpy.linalg as LA
from Dmatrix2d import Dmatrix2d
# 2次元平面応力4節点不適合要素のクラス
class d2cps4i:
# コンストラクタ
# no : 要素番号
# nodes : 節点の集合(Node2d型のリスト)
# thickness : 厚さ
# young : ヤング率
# poisson : ポアソン比
def __init__(self, no, nodes, thickness, young, poisson):
# インスタンス変数を定義する
self.no = no # 要素番号
self.nodes = nodes # nodesは反時計回りの順番になっている前提(Node2d型のリスト形式)
self.thickness = thickness # 厚さ
self.young = young # ヤング率
self.poisson = poisson # ポアソン比
self.ipNum = 4 # 積分点の数
self.w1 = [1.0, 1.0, 1.0, 1.0] # 積分点の重み係数1
self.w2 = [1.0, 1.0, 1.0, 1.0] # 積分点の重み係数2
self.ai = [-np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0)] # 積分点の座標(a,b座標系)
self.bi = [-np.sqrt(1.0 / 3.0), -np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0), np.sqrt(1.0 / 3.0)] # 積分点の座標(a,b座標系)
# Dマトリクスを計算する
self.matD = self.makeDmatrix()
# ヤコビ行列を計算する
self.matJ = []
for i in range(self.ipNum):
self.matJ.append(self.makeJmatrix(self.ai[i], self.bi[i]))
# Bマトリクスを計算する
self.matB = []
for i in range(self.ipNum):
self.matB.append(self.makeBmatrix(self.ai[i], self.bi[i], self.matJ[i]))
# Biマトリクスを計算する
self.matBi = self.makeBimatirixes()
# Kciマトリクスを計算する
self.matKci = self.makeKcimatrix()
# Kiiマトリクスを計算する
self.matKii = self.makeKiimatrix()
# Keマトリクスを作成する
def makeKematrix(self):
# Kccマトリクスをガウス積分で計算する
matKcc = np.matrix(np.zeros([8, 8]))
for i in range(self.ipNum):
matKcc += self.w1[i] * self.w2[i] * self.matB[i].T * self.matD * self.matB[i] * LA.det(self.matJ[i])
matKcc *= self.thickness
# Keマトリクスを計算する
matKe = matKcc - self.matKci * LA.inv(self.matKii) * self.matKci.T
return matKe
# kiiマトリクスを作成する
def makeKiimatrix(self):
matKii = np.matrix(np.zeros([4, 4]))
for i in range(self.ipNum):
matKii += self.w1[i] * self.w2[i] * self.matBi[i].T * self.matD * self.matBi[i] * LA.det(self.matJ[i])
matKii *= self.thickness
return matKii
# Kciマトリクスを作成する
def makeKcimatrix(self):
matKci = np.matrix(np.zeros([8, 4]))
for i in range(self.ipNum):
matKci += self.w1[i] * self.w2[i] * self.matB[i].T * self.matD * self.matBi[i] * LA.det(self.matJ[i])
matKci *= self.thickness
return matKci
# ヤコビ行列を計算する
# ai : a座標値
# bi : b座標値
def makeJmatrix(self, ai, bi):
# dNdabを計算する
dNdab = self.makedNdab(ai, bi)
# xi, yiの行列を計算する
matxiyi = np.matrix([[self.nodes[0].x, self.nodes[0].y],
[self.nodes[1].x, self.nodes[1].y],
[self.nodes[2].x, self.nodes[2].y],
[self.nodes[3].x, self.nodes[3].y]])
# ヤコビ行列を計算する
matJ = dNdab * matxiyi
# ヤコビアンが負にならないかチェックする
if LA.det(matJ) < 0:
raise ValueError("要素の計算に失敗しました")
return matJ
# Dマトリクスを作成する
def makeDmatrix(self):
d2dmat = Dmatrix2d(self.young, self.poisson)
matD = d2dmat.makeDcpsmatrix()
return matD
# Bマトリクスを作成する
# a : a座標値
# b : b座標値
# matJ : 座標(a,b)のヤコビ行列(np.matrix型)
def makeBmatrix(self, a, b, matJ):
# dNdabを計算する
dNdab = self.makedNdab(a, b)
#dNdxy = matJinv * matdNdab
dNdxy = LA.solve(matJ, dNdab)
# Bマトリクスを計算する
matB = np.matrix([[dNdxy[0, 0], 0.0, dNdxy[0, 1], 0.0, dNdxy[0, 2], 0.0, dNdxy[0, 3], 0.0],
[0.0, dNdxy[1, 0], 0.0, dNdxy[1, 1], 0.0, dNdxy[1, 2], 0.0, dNdxy[1, 3]],
[dNdxy[1, 0], dNdxy[0, 0], dNdxy[1, 1], dNdxy[0, 1], dNdxy[1, 2], dNdxy[0, 2], dNdxy[1, 3], dNdxy[0, 3]]])
return matB
# dNdabの行列を計算する
# a : a座標値
# b : b座標値
def makedNdab(self, a, b):
# dNi/da, dNi/dbを計算する
dN1da = -0.25 * (1 - b)
dN2da = 0.25 * (1 - b)
dN3da = 0.25 * (1 + b)
dN4da = -0.25 * (1 + b)
dN1db = -0.25 * (1 - a)
dN2db = -0.25 * (1 + a)
dN3db = 0.25 * (1 + a)
dN4db = 0.25 * (1 - a)
# dNdabを計算する
dNdab = np.matrix([[dN1da, dN2da, dN3da, dN4da],
[dN1db, dN2db, dN3db, dN4db]])
return dNdab
# 補正されたBiマトリクスのリストを作成する
def makeBimatirixes(self):
# Biマトリクスを計算する
matBi = []
sumdetJ = 0
sumMatBidetJ = np.zeros((3, 4))
for i in range(self.ipNum):
matJinv = LA.inv(self.matJ[i])
dadx = matJinv[0,0]
dbdx = matJinv[0,1]
dady = matJinv[1,0]
dbdy = matJinv[1,1]
matBiTmp = np.matrix([[-2 * self.ai[i] * dadx, -2 * self.bi[i] * dbdx, 0, 0],
[0, 0, -2 * self.ai[i] * dady, -2 * self.bi[i] * dbdy],
[-2 * self.ai[i] * dady, -2 * self.bi[i] * dbdy, -2 * self.ai[i] * dadx, -2 * self.bi[i] * dbdx]])
matBi.append(matBiTmp)
# 補正項を求めるためにガウス積分を計算する
sumdetJ += self.w1[i] * self.w2[i] * LA.det(self.matJ[i])
sumMatBidetJ += self.w1[i] * self.w2[i] * matBiTmp * LA.det(self.matJ[i])
# Biマトリクスに補正項を追加する
matBic = -sumMatBidetJ / sumdetJ
for i in range(self.ipNum):
matBi[i] += matBic
return matBi
# 要素の出力データを作成する
# vecElemDisp : 要素節点の変位のリスト
def makeOutputData(self, vecElemDisp):
# 積分点の応力、ひずみを計算する
vecIpStrains = [] # 積分点のひずみベクトルのリスト(np.array型のリスト)
vecIpStresses = [] # 積分点の応力ベクトルのリスト(np.array型のリスト)
ipMises = [] # 積分点のミーゼス応力のリスト
for i in range(self.ipNum):
# 積分点のひずみベクトルを計算する
vec1 = np.array(self.matB[i] @ vecElemDisp).flatten()
vec2 = np.array(self.matBi[i] * LA.inv(self.matKii) * self.matKci.T @ vecElemDisp).flatten()
vecIpStrain = vec1 - vec2
vecIpStrains.append(vecIpStrain)
# 積分点の応力ベクトルを計算する
vecIpStress = np.array(self.matD @ vecIpStrains[i]).flatten()
vecIpStresses.append(vecIpStress)
# 積分点のミーゼス応力を計算する
tmp = np.square(vecIpStress[0] - vecIpStress[1]) + np.square(vecIpStress[0]) + np.square(vecIpStress[1]) + 6 * np.square(vecIpStress[2])
mises = np.sqrt(0.5 * tmp)
ipMises.append(mises)
return vecIpStrains, vecIpStresses, ipMises
Boundary2dクラス
境界条件を格納するためのクラスです。このクラスでは単点拘束、多点拘束、節点に負荷する荷重を設定することが可能です。多点拘束についてはこちらの記事を参照ください。
addSPC関数で単点拘束を追加、addMPC関数で多点拘束を追加、荷重はaddForce関数で追加します。makeDispVector関数、makeForceVector関数とmakeMPCmatrixes関数はFEM2dクラス内で使うための関数で、設定した拘束条件を行列、ベクトルの形で返します。
Boundary2d.py
import numpy as np
class Boundary2d:
# コンストラクタ
# nodeNum : 節点数
def __init__(self, nodeNum):
# インスタンス変数を定義する
self.nodeNum = nodeNum # 全節点数
self.dispNodeNo = [] # 単点拘束の節点番号
self.dispX = [] # 単点拘束の強制変位x
self.dispY = [] # 単点拘束の強制変位y
self.forceNodeNo = [] # 荷重が作用する節点番号
self.forceX = [] # x方向の荷重
self.forceY = [] # y方向の荷重
self.matC = np.empty((0, self.nodeNum * 2)) # 多点拘束用のCマトリクス
self.vecd = np.empty(0) # 多点拘束用のdベクトル
# 単点拘束を追加する
def addSPC(self, nodeNo, x, y):
self.dispNodeNo.append(nodeNo)
self.dispX.append(x)
self.dispY.append(y)
# 多点拘束を追加する
# 条件式 : vecC x u = d
def addMPC(self, vecC, d):
self.matC = np.vstack((self.matC, vecC))
self.vecd = np.hstack((self.vecd, d))
# 単点拘束条件から変位ベクトルを作成する
def makeDispVector(self):
vecd = np.array([None] * self.nodeNum * 2)
for i in range(len(self.dispNodeNo)):
vecd[(self.dispNodeNo[i] - 1) * 2] = self.dispX[i]
vecd[(self.dispNodeNo[i] - 1) * 2 + 1] = self.dispY[i]
return vecd
# 荷重を追加する
def addForce(self, nodeNo, fx, fy):
self.forceNodeNo.append(nodeNo)
self.forceX.append(fx)
self.forceY.append(fy)
# 境界条件から荷重ベクトルを作成する
def makeForceVector(self):
vecf = np.array(np.zeros([self.nodeNum * 2]))
for i in range(len(self.forceNodeNo)):
vecf[(self.forceNodeNo[i] - 1) * 2] += self.forceX[i]
vecf[(self.forceNodeNo[i] - 1) * 2 + 1] += self.forceY[i]
return vecf
# 多点拘束の境界条件を表すCマトリクス、dベクトルを作成する
def makeMPCmatrixes(self):
return self.matC, self.vecd
# 拘束条件を出力する
def printBoundary(self):
print("Node Number: ", self.nodeNum)
print("SPC Constraint Condition")
for i in range(len(self.dispNodeNo)):
print("Node No: " + str(self.dispNodeNo[i]) + ", x: " + str(self.dispX[i]) + ", y: " + str(self.dispY[i]))
print("Force Condition")
for i in range(len(self.forceNodeNo)):
print("Node No: " + str(self.forceNodeNo[i]) + ", x: " + str(self.forceX[i]) + ", y: " + str(self.forceY[i]))
print("MPC Constraint Condition")
print("C x u = q")
print("C Matrix")
print(self.matC)
print("q vector")
print(self.vecd)
FEM2dクラス
有限要素法の解析を行うクラスです。
analysis関数で要素剛性マトリクスから全体剛性マトリクスを作成し、節点変位を求めた後に、各要素の積分点での応力、ひずみ、ミーゼス応力を求めます。
そして解析した結果はoutputTxt関数でテキスト形式で出力することができます。
全体剛性マトリクスの作成から節点変位を求める方法については
こちらの記事をご参照ください。
三角形要素とほぼ同様の方法で求めることが可能です。
FEM2d.py
import numpy as np
import numpy.linalg as LA
from Boundary2d import Boundary2d
class FEM2d:
# コンストラクタ
# nodes : 全節点のリスト(節点は1から始まる順番で並んでいる前提, Node2d型のリスト)
# elements : 全要素のリスト(d2cps4iのリスト)
# bound : 境界条件(d2Boundary型)
def __init__(self, nodes, elements, bound):
self.nodes = nodes # 全節点のリスト(Node2d型のリスト)
self.elements = elements # 全要素のリスト(d2cps4iのリスト)
self.bound = bound # 境界条件(d2Boundary型)
# 解析を行う
def analysis(self):
# 境界条件を考慮しないKマトリクスを作成する
matK = self.makeKmatrix()
# 節点に負荷する荷重ベクトルを作成する
vecf = self.bound.makeForceVector()
# 境界条件を考慮したKマトリクス、荷重ベクトルを作成する
matKc, vecfc, condiNum = self.setBoundCondition(matK, vecf)
# 変位ベクトルを計算する
vecTmp = LA.solve(matKc, vecfc)
vecDisp = np.delete(vecTmp, slice(len(vecTmp) - condiNum, len(vecTmp)))
self.vecDisp = vecDisp
# 変位ベクトルから要素の出力データを計算する
vecIpStrainsList = []
vecIpStressList = []
ipMisesList = []
for elem in self.elements:
vecElemDisp = np.zeros(len(elem.nodes) * 2)
for i in range(len(elem.nodes)):
vecElemDisp[i * 2] = vecDisp[(elem.nodes[i].no - 1) * 2]
vecElemDisp[i * 2 + 1] = vecDisp[(elem.nodes[i].no - 1) * 2 + 1]
vecIpStrains, vecIpStresses, ipMises = elem.makeOutputData(vecElemDisp)
vecIpStrainsList.append(vecIpStrains)
vecIpStressList.append(vecIpStresses)
ipMisesList.append(ipMises)
self.vecIpStrainsList = vecIpStrainsList
self.vecIpStressList = vecIpStressList
self.ipMisesList = ipMisesList
# 節点反力を計算する
vecRF = np.array(matK @ vecDisp - vecf).flatten()
self.vecRF = vecRF
# 境界条件を考慮しないKマトリクスを作成する
def makeKmatrix(self):
matK = np.matrix(np.zeros((len(self.nodes) * 2, len(self.nodes) * 2)))
for elem in self.elements:
# keマトリクスを計算する
matKe = elem.makeKematrix()
# Kマトリクスに代入する
for c in range(len(elem.nodes) * 2):
ct = (elem.nodes[c // 2].no - 1) * 2 + c % 2
for r in range(len(elem.nodes) * 2):
rt = (elem.nodes[r // 2].no - 1) * 2 + r % 2
matK[ct, rt] += matKe[c, r]
return matK
# Kマトリクス、荷重ベクトルに境界条件を考慮する
def setBoundCondition(self, matK, vecf):
matKc = np.copy(matK)
vecfc = np.copy(vecf)
# 単点拘束条件を考慮したKマトリクス、荷重ベクトルを作成する
vecDisp = self.bound.makeDispVector()
for i in range(len(vecDisp)):
if not vecDisp[i] == None:
# Kマトリクスからi列を抽出する
vecx = np.array(matK[:, i]).flatten()
# 変位ベクトルi列の影響を荷重ベクトルに適用する
vecfc = vecfc - vecDisp[i] * vecx
# Kマトリクスのi行、i列を全て0にし、i行i列の値を1にする
matKc[:, i] = 0.0
matKc[i, :] = 0.0
matKc[i, i] = 1.0
for i in range(len(vecDisp)):
if not vecDisp[i] == None:
vecfc[i] = vecDisp[i]
# 多節点拘束条件を考慮したKマトリクス、荷重ベクトルを作成する
matC, vecd = self.bound.makeMPCmatrixes()
mpcNum = len(vecd) # 多節点拘束の条件式の数を求める
if mpcNum > 0:
matKc = np.hstack((matKc, matC.T))
tmpMat = np.hstack((matC, np.zeros((matC.shape[0], matC.shape[0]))))
matKc = np.vstack((matKc, tmpMat))
vecfc = np.hstack((vecf, vecd))
return matKc, vecfc, mpcNum
# 解析結果をテキストファイルに出力する
def outputTxt(self, filePath):
# ファイルを作成し、開く
f = open(filePath + ".txt", 'w')
# 出力する文字の情報を定義する
columNum = 18
floatDigits = ".10g"
# 入力データのタイトルを書きこむ
f.write("*********************************\n")
f.write("* Input Data *\n")
f.write("*********************************\n")
f.write("\n")
# 節点情報を出力する
f.write("***** Node Data ******\n")
f.write("No".rjust(columNum) + "X".rjust(columNum) + "Y".rjust(columNum) + "\n")
f.write("-" * columNum * 3 + "\n")
for node in self.nodes:
strNo = str(node.no).rjust(columNum)
strX = str(format(node.x, floatDigits).rjust(columNum))
strY = str(format(node.y, floatDigits).rjust(columNum))
f.write(strNo + strX + strY + "\n")
f.write("\n")
# 要素情報を出力する
f.write("***** Element Data ******\n")
f.write("No".rjust(columNum) + "Type".rjust(columNum) + "Node No".rjust(columNum) +
"Thickness".rjust(columNum) + "Young".rjust(columNum) + "Poisson".rjust(columNum) + "\n")
f.write("-" * columNum * 6 + "\n")
for elem in self.elements:
strNo = str(elem.no).rjust(columNum)
strType = str(elem.__class__.__name__ ).rjust(columNum)
strNodeNo = ""
for node in elem.nodes:
strNodeNo += " " + str(node.no)
strNodeNo = strNodeNo.rjust(columNum)
strThickness = str(format(elem.thickness, floatDigits).rjust(columNum))
strYoung = str(format(elem.young, floatDigits).rjust(columNum))
strPoisson = str(format(elem.poisson, floatDigits).rjust(columNum))
f.write(strNo + strType + strNodeNo + strThickness + strYoung + strPoisson + "\n")
f.write("\n")
# 単点拘束情報を出力する
f.write("***** SPC Constraint Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Displacement".rjust(columNum) + "Y Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 3 + "\n")
for i in range(len(self.bound.dispNodeNo)):
strNo = str(self.bound.dispNodeNo[i]).rjust(columNum)
strXDisp = "None".rjust(columNum)
if not self.bound.dispX[i] is None:
strXDisp = str(format(self.bound.dispX[i], floatDigits).rjust(columNum))
strYDisp = "None".rjust(columNum)
if not self.bound.dispY[i] is None:
strYDisp = str(format(self.bound.dispY[i], floatDigits).rjust(columNum))
f.write(strNo + strXDisp + strYDisp + "\n")
f.write("\n")
# 多点拘束情報を出力する
matC, vecd = self.bound.makeMPCmatrixes()
f.write("***** MPC Constraint Data ******\n")
f.write("-" * columNum * 1 + "\n")
for i in range(matC.shape[0]):
strRow = ""
for j in range(matC.shape[1]):
if not matC[i, j] == 0:
strTmp = " " + str(format(matC[i, j], "+.3g"))
if (j % 2) == 0:
strTmp += " u" + str(j // 2 + 1)
else :
strTmp += " v" + str(j // 2 + 1)
strRow += strTmp.rjust(5)
strRow += "= " + str(format(vecd[i], ".3g"))
f.write(strRow + "\n")
f.write("\n")
# 荷重条件を出力する
f.write("***** Nodal Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "X Force".rjust(columNum) + "Y Force".rjust(columNum) + "\n")
f.write("-" * columNum * 3 + "\n")
vecf = self.bound.makeForceVector()
for i in range(len(self.nodes)):
if not vecf[2 * i] == 0 or not vecf[2 * i + 1] == 0:
strNo = str(i + 1).rjust(columNum)
strXForce = str(format(vecf[2 * i], floatDigits).rjust(columNum))
strYForce = str(format(vecf[2 * i + 1], floatDigits).rjust(columNum))
f.write(strNo + strXForce + strYForce + "\n")
f.write("\n")
# 結果データのタイトルを書きこむ
f.write("**********************************\n")
f.write("* Result Data *\n")
f.write("**********************************\n")
f.write("\n")
# 変位のデータを出力する
f.write("***** Displacement Data ******\n")
f.write("NodeNo".rjust(columNum) + "Magnitude".rjust(columNum) + "X Displacement".rjust(columNum) +
"Y Displacement".rjust(columNum) + "\n")
f.write("-" * columNum * 4 + "\n")
for i in range(len(self.nodes)):
strNo = str(i + 1).rjust(columNum)
mag = np.linalg.norm(np.array((self.vecDisp[2 * i], self.vecDisp[2 * i + 1])))
strMag = str(format(mag, floatDigits).rjust(columNum))
strXDisp = str(format(self.vecDisp[2 * i], floatDigits).rjust(columNum))
strYDisp = str(format(self.vecDisp[2 * i + 1], floatDigits).rjust(columNum))
f.write(strNo + strMag + strXDisp + strYDisp + "\n")
f.write("\n")
# 応力データを出力する
f.write("***** Stress Data ******\n")
f.write("Element No".rjust(columNum) + "Integral No".rjust(columNum) + "Stress XX".rjust(columNum) + "Stress YY".rjust(columNum) +
"Stress XY".rjust(columNum) + "Mises".rjust(columNum) + "\n")
f.write("-" * columNum * 6 + "\n")
for i in range(len(self.elements)):
elem = self.elements[i]
strElemNo = str(elem.no).rjust(columNum)
for j in range(elem.ipNum):
strIntNo = str(j + 1).rjust(columNum)
vecIpStresses = self.vecIpStressList[i]
strStressXX = str(format(vecIpStresses[j][0], floatDigits).rjust(columNum))
strStressYY = str(format(vecIpStresses[j][1], floatDigits).rjust(columNum))
strStressXY = str(format(vecIpStresses[j][2], floatDigits).rjust(columNum))
ipMises = self.ipMisesList[i]
strMises = str(format(ipMises[j], floatDigits).rjust(columNum))
f.write(strElemNo + strIntNo + strStressXX + strStressYY + strStressXY + strMises + "\n")
f.write("\n")
# ひずみデータを出力する
f.write("***** Strain Data ******\n")
f.write("Element No".rjust(columNum) + "Integral No".rjust(columNum) + "Strain XX".rjust(columNum) + "Strain YY".rjust(columNum) +
"Strain XY".rjust(columNum) + "\n")
f.write("-" * columNum * 5 + "\n")
for i in range(len(self.elements)):
elem = self.elements[i]
strElemNo = str(elem.no).rjust(columNum)
for j in range(elem.ipNum):
strIntNo = str(j + 1).rjust(columNum)
vecIpStrains = self.vecIpStrainsList[i]
strStrainXX = str(format(vecIpStrains[j][0], floatDigits).rjust(columNum))
strStrainYY = str(format(vecIpStrains[j][1], floatDigits).rjust(columNum))
strStrainXY = str(format(vecIpStrains[j][2], floatDigits).rjust(columNum))
f.write(strElemNo + strIntNo + strStrainXX + strStrainYY + strStrainXY + "\n")
f.write("\n")
# 反力のデータを出力する
f.write("***** Reaction Force Data ******\n")
f.write("NodeNo".rjust(columNum) + "Magnitude".rjust(columNum) + "X Force".rjust(columNum) + "Y Force".rjust(columNum) + "\n")
f.write("-" * columNum * 4 + "\n")
for i in range(len(self.nodes)):
strNo = str(i + 1).rjust(columNum)
mag = np.linalg.norm(np.array((self.vecRF[2 * i], self.vecRF[2 * i + 1])))
strMag = str(format(mag, floatDigits).rjust(columNum))
strXForce = str(format(self.vecRF[2 * i], floatDigits).rjust(columNum))
strYForce = str(format(self.vecRF[2 * i + 1], floatDigits).rjust(columNum))
f.write(strNo + strMag + strXForce + strYForce + "\n")
f.write("\n")
# ファイルを閉じる
f.close()
簡単な例題でテストする
ようやく非適合要素の解析を行うためのクラスが実装できたので、そのクラスを使って簡単な例題をテストしてみます。今回は下の図の例題で解析を行ってみます。
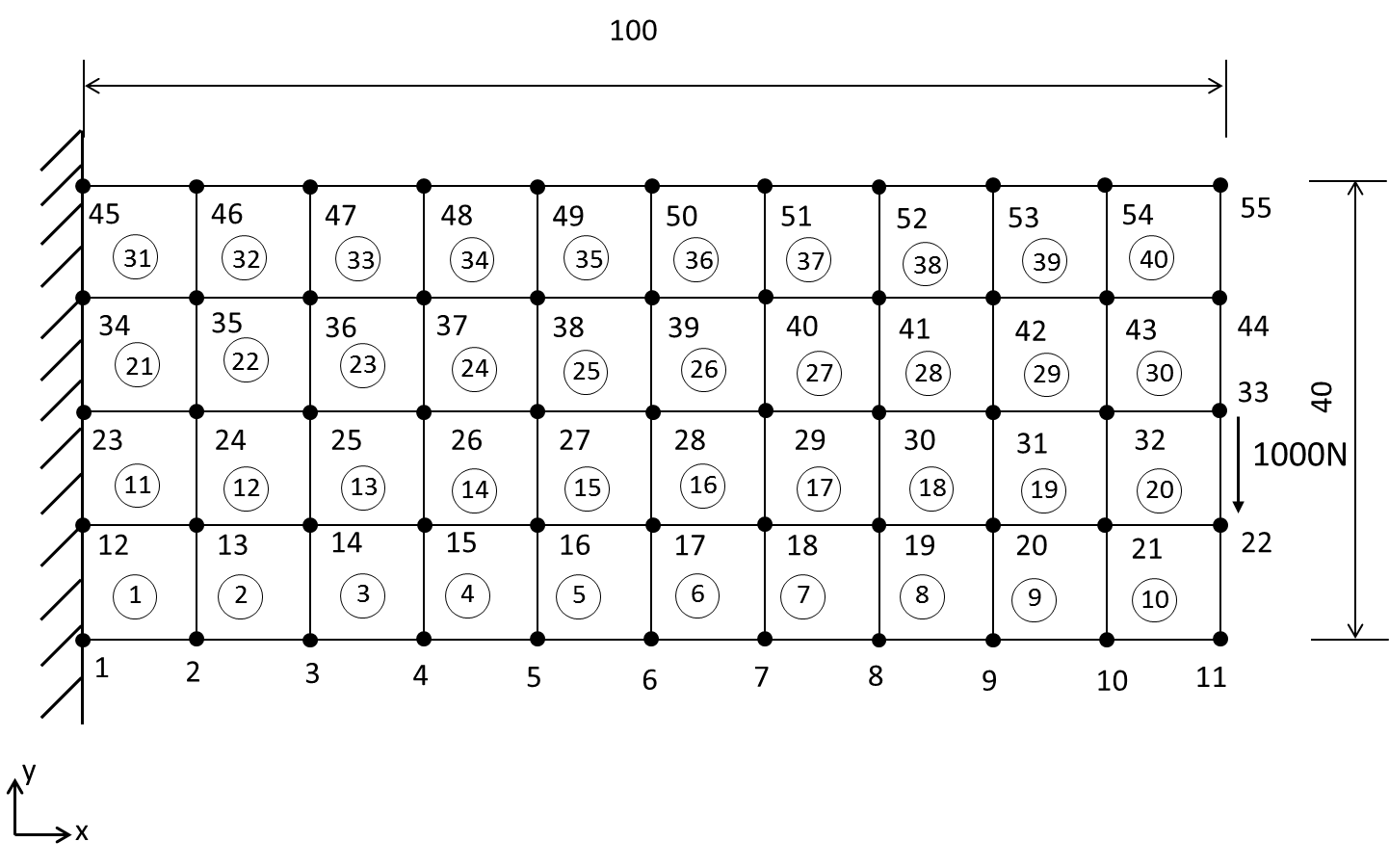
要素は全て平面応力状態の4節点の非適合要素で形状は10mmの正方形、厚さは1.5mmとして、ヤング率は210000Mpa、ポアソン比は0.3とします。境界条件は節点1,12,23,34,45を完全固定、節点33にy軸方向の集中荷重-1000Nを負荷します。
この例題を解くメイン処理をPythonで実装してみます。
main.py
from Node2d import Node2d
from d2cps4i import d2cps4i
from Boundary2d import Boundary2d
from FEM2d import FEM2d
def main():
# 節点リストを定義する
node1 = Node2d(1, 0.0, 0.0)
node2 = Node2d(2, 10.0, 0.0)
node3 = Node2d(3, 20.0, 0.0)
node4 = Node2d(4, 30.0, 0.0)
node5 = Node2d(5, 40.0, 0.0)
node6 = Node2d(6, 50.0, 0.0)
node7 = Node2d(7, 60.0, 0.0)
node8 = Node2d(8, 70.0, 0.0)
node9 = Node2d(9, 80.0, 0.0)
node10 = Node2d(10, 90.0, 0.0)
node11 = Node2d(11, 100.0, 0.0)
node12 = Node2d(12, 0.0, 10.0)
node13 = Node2d(13, 10.0, 10.0)
node14 = Node2d(14, 20.0, 10.0)
node15 = Node2d(15, 30.0, 10.0)
node16 = Node2d(16, 40.0, 10.0)
node17 = Node2d(17, 50.0, 10.0)
node18 = Node2d(18, 60.0, 10.0)
node19 = Node2d(19, 70.0, 10.0)
node20 = Node2d(20, 80.0, 10.0)
node21 = Node2d(21, 90.0, 10.0)
node22 = Node2d(22, 100.0, 10.0)
node23 = Node2d(23, 0.0, 20.0)
node24 = Node2d(24, 10.0, 20.0)
node25 = Node2d(25, 20.0, 20.0)
node26 = Node2d(26, 30.0, 20.0)
node27 = Node2d(27, 40.0, 20.0)
node28 = Node2d(28, 50.0, 20.0)
node29 = Node2d(29, 60.0, 20.0)
node30 = Node2d(30, 70.0, 20.0)
node31 = Node2d(31, 80.0, 20.0)
node32 = Node2d(32, 90.0, 20.0)
node33 = Node2d(33, 100.0, 20.0)
node34 = Node2d(34, 0.0, 30.0)
node35 = Node2d(35, 10.0, 30.0)
node36 = Node2d(36, 20.0, 30.0)
node37 = Node2d(37, 30.0, 30.0)
node38 = Node2d(38, 40.0, 30.0)
node39 = Node2d(39, 50.0, 30.0)
node40 = Node2d(40, 60.0, 30.0)
node41 = Node2d(41, 70.0, 30.0)
node42 = Node2d(42, 80.0, 30.0)
node43 = Node2d(43, 90.0, 30.0)
node44 = Node2d(44, 100.0, 30.0)
node45 = Node2d(45, 0.0, 40.0)
node46 = Node2d(46, 10.0, 40.0)
node47 = Node2d(47, 20.0, 40.0)
node48 = Node2d(48, 30.0, 40.0)
node49 = Node2d(49, 40.0, 40.0)
node50 = Node2d(50, 50.0, 40.0)
node51 = Node2d(51, 60.0, 40.0)
node52 = Node2d(52, 70.0, 40.0)
node53 = Node2d(53, 80.0, 40.0)
node54 = Node2d(54, 90.0, 40.0)
node55 = Node2d(55, 100.0, 40.0)
nodes = [node1, node2, node3, node4, node5, node6, node7, node8, node9, node10,
node11, node12, node13, node14, node15, node16, node17, node18, node19, node20,
node21, node22, node23, node24, node25, node26, node27, node28, node29, node30,
node31, node32, node33, node34, node35, node36, node37, node38, node39, node40,
node41, node42, node43, node44, node45, node46, node47, node48, node49, node50,
node51, node52, node53, node54, node55]
nodes1 = [node1, node2, node13, node12]
nodes2 = [node2, node3, node14, node13]
nodes3 = [node3, node4, node15, node14]
nodes4 = [node4, node5, node16, node15]
nodes5 = [node5, node6, node17, node16]
nodes6 = [node6, node7, node18, node17]
nodes7 = [node7, node8, node19, node18]
nodes8 = [node8, node9, node20, node19]
nodes9 = [node9, node10, node21, node20]
nodes10 = [node10, node11, node22, node21]
nodes11 = [node12, node13, node24, node23]
nodes12 = [node13, node14, node25, node24]
nodes13 = [node14, node15, node26, node25]
nodes14 = [node15, node16, node27, node26]
nodes15 = [node16, node17, node28, node27]
nodes16 = [node17, node18, node29, node28]
nodes17 = [node18, node19, node30, node29]
nodes18 = [node19, node20, node31, node30]
nodes19 = [node20, node21, node32, node31]
nodes20 = [node21, node22, node33, node32]
nodes21 = [node23, node24, node35, node34]
nodes22 = [node24, node25, node36, node35]
nodes23 = [node25, node26, node37, node36]
nodes24 = [node26, node27, node38, node37]
nodes25 = [node27, node28, node39, node38]
nodes26 = [node28, node29, node40, node39]
nodes27 = [node29, node30, node41, node40]
nodes28 = [node30, node31, node42, node41]
nodes29 = [node31, node32, node43, node42]
nodes30 = [node32, node33, node44, node43]
nodes31 = [node34, node35, node46, node45]
nodes32 = [node35, node36, node47, node46]
nodes33 = [node36, node37, node48, node47]
nodes34 = [node37, node38, node49, node48]
nodes35 = [node38, node39, node50, node49]
nodes36 = [node39, node40, node51, node50]
nodes37 = [node40, node41, node52, node51]
nodes38 = [node41, node42, node53, node52]
nodes39 = [node42, node43, node54, node53]
nodes40 = [node43, node44, node55, node54]
# 要素セットを定義する
thickness = 1.5
young = 210000
poisson = 0.3
elem1 = d2cps4i(1, nodes1, thickness, young, poisson)
elem2 = d2cps4i(2, nodes2, thickness, young, poisson)
elem3 = d2cps4i(3, nodes3, thickness, young, poisson)
elem4 = d2cps4i(4, nodes4, thickness, young, poisson)
elem5 = d2cps4i(5, nodes5, thickness, young, poisson)
elem6 = d2cps4i(6, nodes6, thickness, young, poisson)
elem7 = d2cps4i(7, nodes7, thickness, young, poisson)
elem8 = d2cps4i(8, nodes8, thickness, young, poisson)
elem9 = d2cps4i(9, nodes9, thickness, young, poisson)
elem10 = d2cps4i(10, nodes10, thickness, young, poisson)
elem11 = d2cps4i(11, nodes11, thickness, young, poisson)
elem12 = d2cps4i(12, nodes12, thickness, young, poisson)
elem13 = d2cps4i(13, nodes13, thickness, young, poisson)
elem14 = d2cps4i(14, nodes14, thickness, young, poisson)
elem15 = d2cps4i(15, nodes15, thickness, young, poisson)
elem16 = d2cps4i(16, nodes16, thickness, young, poisson)
elem17 = d2cps4i(17, nodes17, thickness, young, poisson)
elem18 = d2cps4i(18, nodes18, thickness, young, poisson)
elem19 = d2cps4i(19, nodes19, thickness, young, poisson)
elem20 = d2cps4i(20, nodes20, thickness, young, poisson)
elem21 = d2cps4i(21, nodes21, thickness, young, poisson)
elem22 = d2cps4i(22, nodes22, thickness, young, poisson)
elem23 = d2cps4i(23, nodes23, thickness, young, poisson)
elem24 = d2cps4i(24, nodes24, thickness, young, poisson)
elem25 = d2cps4i(25, nodes25, thickness, young, poisson)
elem26 = d2cps4i(26, nodes26, thickness, young, poisson)
elem27 = d2cps4i(27, nodes27, thickness, young, poisson)
elem28 = d2cps4i(28, nodes28, thickness, young, poisson)
elem29 = d2cps4i(29, nodes29, thickness, young, poisson)
elem30 = d2cps4i(30, nodes30, thickness, young, poisson)
elem31 = d2cps4i(31, nodes31, thickness, young, poisson)
elem32 = d2cps4i(32, nodes32, thickness, young, poisson)
elem33 = d2cps4i(33, nodes33, thickness, young, poisson)
elem34 = d2cps4i(34, nodes34, thickness, young, poisson)
elem35 = d2cps4i(35, nodes35, thickness, young, poisson)
elem36 = d2cps4i(36, nodes36, thickness, young, poisson)
elem37 = d2cps4i(37, nodes37, thickness, young, poisson)
elem38 = d2cps4i(38, nodes38, thickness, young, poisson)
elem39 = d2cps4i(39, nodes39, thickness, young, poisson)
elem40 = d2cps4i(40, nodes40, thickness, young, poisson)
elems = [elem1, elem2, elem3, elem4, elem5, elem6, elem7, elem8, elem9, elem10,
elem11, elem12, elem13, elem14, elem15, elem16, elem17, elem18, elem19, elem20,
elem21, elem22, elem23, elem24, elem25, elem26, elem27, elem28, elem29, elem30,
elem31, elem32, elem33, elem34, elem35, elem36, elem37, elem38, elem39, elem40]
# 境界条件を設定する
bound = Boundary2d(len(nodes))
bound.addSPC(1, 0.0, 0.0)
bound.addSPC(12, 0.0, 0.0)
bound.addSPC(23, 0.0, 0.0)
bound.addSPC(34, 0.0, 0.0)
bound.addSPC(45, 0.0, 0.0)
bound.addForce(33, 0.0, -1000.0)
# 解析を行う
fem = FEM2d(nodes, elems, bound)
fem.analysis()
# Txt形式で結果を出力する
fem.outputTxt("output")
main()
結果はoutput.txtファイルに出力されます。
得られた結果が正しいか、Abaqus Student Edition2021を使用して確かめてみます。Abaqusではcps4i要素が4節点平面応力の非適合要素になります。
Abaqusの入力ファイル
*node
1, 0.0, 0.0
2, 10.0, 0.0
3, 20.0, 0.0
4, 30.0, 0.0
5, 40.0, 0.0
6, 50.0, 0.0
7, 60.0, 0.0
8, 70.0, 0.0
9, 80.0, 0.0
10, 90.0, 0.0
11, 100.0, 0.0
12, 0.0, 10.0
13, 10.0, 10.0
14, 20.0, 10.0
15, 30.0, 10.0
16, 40.0, 10.0
17, 50.0, 10.0
18, 60.0, 10.0
19, 70.0, 10.0
20, 80.0, 10.0
21, 90.0, 10.0
22, 100.0, 10.0
23, 0.0, 20.0
24, 10.0, 20.0
25, 20.0, 20.0
26, 30.0, 20.0
27, 40.0, 20.0
28, 50.0, 20.0
29, 60.0, 20.0
30, 70.0, 20.0
31, 80.0, 20.0
32, 90.0, 20.0
33, 100.0, 20.0
34, 0.0, 30.0
35, 10.0, 30.0
36, 20.0, 30.0
37, 30.0, 30.0
38, 40.0, 30.0
39, 50.0, 30.0
40, 60.0, 30.0
41, 70.0, 30.0
42, 80.0, 30.0
43, 90.0, 30.0
44, 100.0, 30.0
45, 0.0, 40.0
46, 10.0, 40.0
47, 20.0, 40.0
48, 30.0, 40.0
49, 40.0, 40.0
50, 50.0, 40.0
51, 60.0, 40.0
52, 70.0, 40.0
53, 80.0, 40.0
54, 90.0, 40.0
55, 100.0, 40.0
*element, type=cps4i, elset=allelems
1, 1, 2, 13, 12
2, 2, 3, 14, 13
3, 3, 4, 15, 14
4, 4, 5, 16, 15
5, 5, 6, 17, 16
6, 6, 7, 18, 17
7, 7, 8, 19, 18
8, 8, 9, 20, 19
9, 9, 10, 21, 20
10, 10, 11, 22, 21
11, 12, 13, 24, 23
12, 13, 14, 25, 24
13, 14, 15, 26, 25
14, 15, 16, 27, 26
15, 16, 17, 28, 27
16, 17, 18, 29, 28
17, 18, 19, 30, 29
18, 19, 20, 31, 30
19, 20, 21, 32, 31
20, 21, 22, 33, 32
21, 23, 24, 35, 34
22, 24, 25, 36, 35
23, 25, 26, 37, 36
24, 26, 27, 38, 37
25, 27, 28, 39, 38
26, 28, 29, 40, 39
27, 29, 30, 41, 40
28, 30, 31, 42, 41
29, 31, 32, 43, 42
30, 32, 33, 44, 43
31, 34, 35, 46, 45
32, 35, 36, 47, 46
33, 36, 37, 48, 47
34, 37, 38, 49, 48
35, 38, 39, 50, 49
36, 39, 40, 51, 50
37, 40, 41, 52, 51
38, 41, 42, 53, 52
39, 42, 43, 54, 53
40, 43, 44, 55, 54
*material, name=mat
*elastic
210000, 0.3
*solid section, material=mat, elset=allelems
1.5
*boundary
1, 1, 2
12, 1, 2
23, 1, 2
34, 1, 2
45, 1, 2
*step
*static
*cload
33, 2, -1000.0
*end step
全ての節点、要素の値の比較は載せきれないので、値が大きい節点と要素の値で比較してみます。
いずれの結果も$10^{-2}$オーダーまでは一致することが確認できます。
実装したコードは下記にもアップロードしています。
Altaka4128/FEM2d_IC
参考文献
有限要素法の「常識」〔固体・構造編〕
INCOMPATIBLE ELEMENTS
Finite element modelling of structural mechanics problems
計算破壊力学のための応用有限要素法プログラム実装




