機械学習
1.機械学習の課題
機械学習
画像・言語・音声などの様々なデータの背景に潜むルールやパターンを獲得する手法、コンピュータに大量のデータを「学習」させることでルールやパターンを獲得しそれらを基に未知のデータを予測・解析する
訓練誤差:学習データに対する予測と正解の誤差
汎化誤差:未知のデータに対する予測と正解の誤差
過剰適合:機械学習モデルが学習データに過剰に適合し、学習データに対しては高い精度な一方、未知のデータに対して十分な精度が得られない現象⇒モデルの次元が大きすぎる(パラメータ数多い)
過少適合:機械学習モデルが学習データに十分に適合できず、学習データおよび未知のデータに対して十分な精度が得られない現象⇒モデルの次元が小さすぎる(パラメータ数少)
機械学習の課題
適切な次元のモデルを設定する必要がある
データ数が多ければ多いほど、過剰、過少適合の問題は緩和される
過剰過少適合が発生すると、未知のデータに対するモデルの予測が不正確になる
正則化:機械学習モデルの過剰適合を抑制する方法、モデルのパラメータが複雑になりすぎないように制約を加えた状態で学習させる
次元の呪い:機械学習において特徴量の次元の数が大きくなればなるほど、正確に適合するモデルの作成に必要なデータ数が指数関数的に増加し、結果的に学習が難しくなる現象⇒適切な次元に設定が必要
深層学習
機械学習の手法の1つ、人間の神経細胞を模倣した機械学習手法「ニューラルネットワーク」において、層の数を増やして多層にしたもの全般を深層学習と呼ぶ。
深層学習の適用範囲:カテゴリあるデータの分類・画像・言語の認識や生成
深層学習でもほかの機械学習手法と同様に過剰・過少適合が発生する。訓練誤差、汎化誤差の状況から過剰適合・過少適合を判定可能
例:多層ニューラルネットワークの学習状況のグラフ
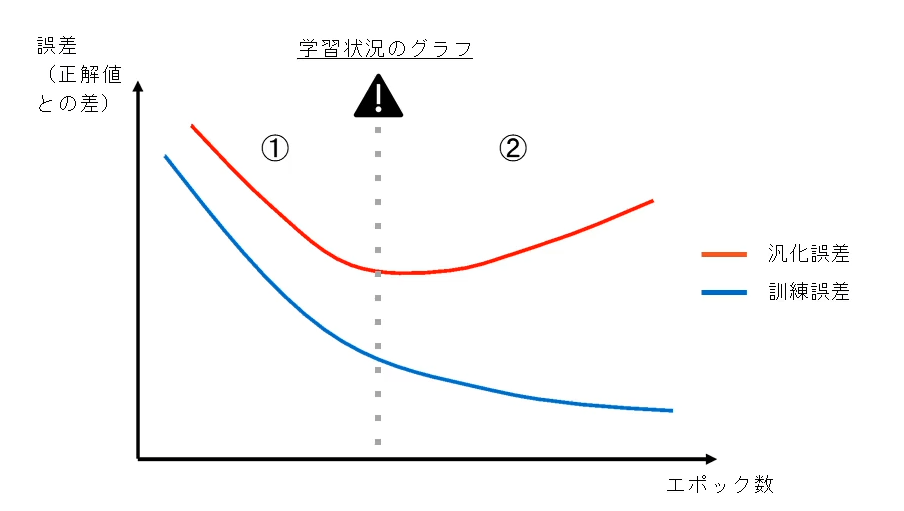
学習状況の見方
①過少適合:訓練誤差と汎化誤差の傾向は同じだが汎化誤差の値が大きい。モデルのパラメータを増やして抑制可能
②過剰適合:訓練誤差と汎化誤差の傾向が異なり、訓練誤差に特化したモデルになっていることを示しており、正則化やモデルのパラメータ巣を減らすなどで抑制可能
2.性能指標
学習済みのロジスティック回帰モデルの性能を測る指標
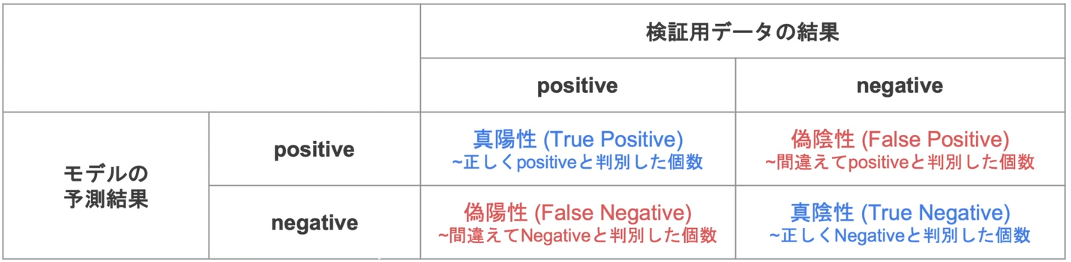
混同行列:各検証データに対するモデルの予測結果を4つの観点で分類し、それぞれに当てはまる予測結果の個数をまとめた表
分類の評価方法
正解率:正解した数/予測対象となった全データ数
再現率(Recall):本当にポジティブなものの中からポジティブと予測できる割合、誤りが多少多くても抜け漏れは少ない予測をしたい際に利用
適合率(Precision):モデルがポジティブと予測したものの中で本当にポジティブである割合、見逃しが多くてもより正確な予測したい際に利用
F値:PrecisionとRecallの調和平均、理想的にはどちらも高いモデルがいいモデルだが、両社はトレードオフの関係にある。
3.線形回帰モデル
回帰問題:ある入力から出力を予測する問題
直線で予測:線形回帰
曲線で予測:非線形回帰
回帰で扱うデータ
入力(各要素を説明変数または特徴量と呼ぶ) m次元のベクトル
出力(目的変数) スカラー値
線形回帰モデル:回帰問題を解くための機械学習モデルの一つ, 教師あり学習, 入力とm次元のパラメータの線形結合を出力するモデル
説明変数が1次元の場合(m=1), 単回帰モデルと呼び, 直線
説明変数型次元の場合(m>1), 重回帰モデルと呼び, 曲線
・線形結合(入力とパラメータの内積):入力ベクトルと未知のパラメータの各要素を足し合わせたもの
・線形回帰モデルのパラメータは最小二乗法で推定
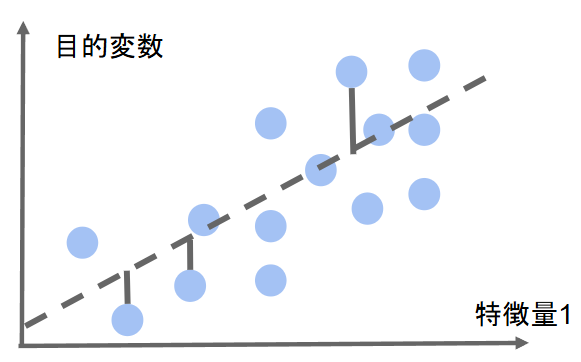
平均二乗誤差(残差平方和):データとモデル出力の二乗誤差
最小二乗法:学習データの平均二乗誤差を最小とするパラメータを探索、勾配が0になる点を求めればよい
実装演習
訓練データ生成
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
n_sample = 100
var = .2
def linear_func(x):
return 2 * x + 5
def add_noise(y_true, var):
return y_true + np.random.normal(scale=var, size=y_true.shape)
def plt_result(xs_train, ys_true, ys_train):
plt.scatter(xs_train, ys_train, facecolor="none", edgecolor="b", s=50, label="training data")
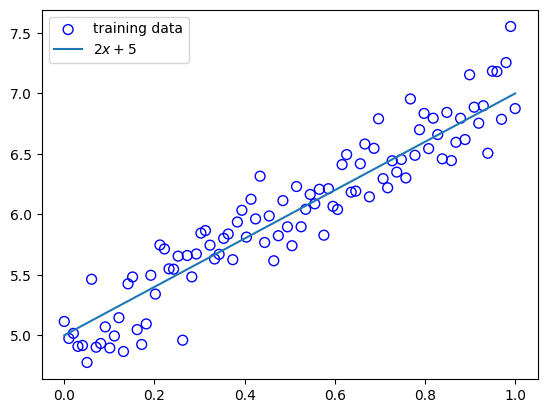
plt.plot(xs_train, ys_true, label="$2 x + 5$")
plt.legend()
#データの作成
xs = np.linspace(0, 1, n_sample)
ys_true = linear_func(xs)
ys = add_noise(ys_true, var)
print("xs: {}".format(xs.shape))
print("ys_true: {}".format(ys_true.shape))
print("ys: {}".format(ys.shape))
#結果の描画
plt_result(xs, ys_true, ys)
予測
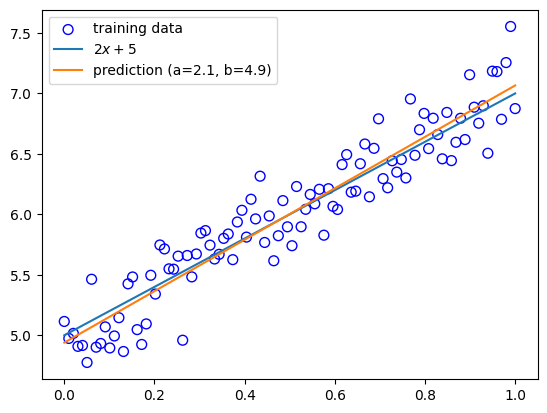
予測の結果, y=2x+5に近い直線となった(a = 2.1, b = 4.9)
xs_new = np.linspace(0, 1, n_sample)
ys_pred = a * xs_new + b
plt.scatter(xs, ys, facecolor="none", edgecolor="b", s=50, label="training data")
plt.plot(xs_new, ys_true, label="$2 x + 5$")
plt.plot(xs_new, ys_pred, label="prediction (a={:.2}, b={:.2})".format(a, b))
plt.legend()
plt.show()
4.非線形回帰モデル
ロジスティック回帰モデル
・同時確率:あるデータが得られた時、それが同時に得られる確率、確率変数は独立であることを仮定すると、それぞれの確率の掛け算となる
・尤度関数:データは固定し、パラメータを変化させる、尤度関数を最大化するようなパラメータを選ぶ推定方法を最尤推定という
ロジスティック回帰モデルの最尤推定
確率pはシグモイド関数となるため、推定するパラメータは重みパラメータとなる。尤度関数Eを最大とするパラメータを探索
⇒尤度関数を最大とするパラメータを探す(推定):対数をとると微分の計算が簡単、対数尤度関数が最大になる点と尤度関数が最大になる点は同じ
「尤度関数にマイナスをかけたものを最小化」し、「最小二乗法の最小化と合わせる」
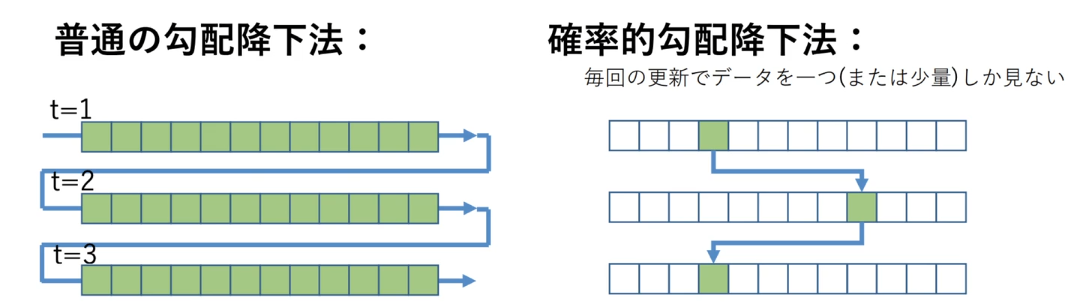
勾配降下法:反復学習によりパラメータを逐次的に更新するアプローチの一つ、学習率というハイパーパラメータでモデルのパラメータの収束しやすさを調整
確率的勾配降下法(SGD):データを一つずつランダムに選んでパラメータを更新、パラメータを一回更新するのと同じ計算量でパラメータをn回更新できるので効率よく最適な解を探索可能
5.主成分分析、K近傍法、K-means
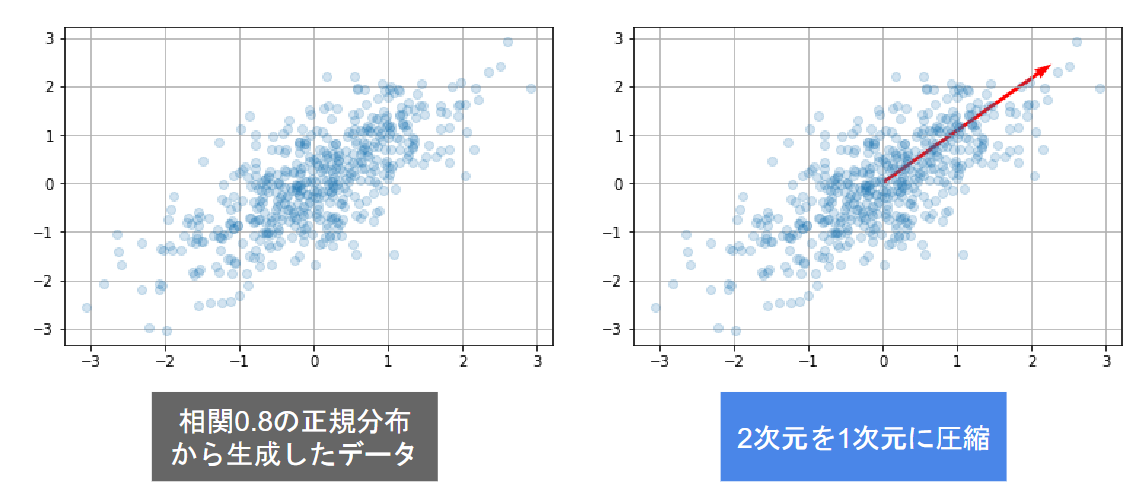
主成分分析:多変量データの持つ構造をより少数個の指標に圧縮 ⇒ 変数の個数を減らすことに伴う、情報の損失はなるべく小さく、少数変数を利用した分析や可視化が実現可能
主成分分析のおおまかな流れ
学習データ ⇒ 平均(ベクトル) ⇒ データ行列 ⇒ 分散共分散行列 ⇒ 線形変換後のベクトル
情報のロスを少なく ⇒ 係数ベクトルが変われば線形変換後の値が変化 ⇒ 線形変換後の変数の分散が最大となるような射影軸を探索
・制約付き最適化問題を解く
ノルムが1となる制約を入れる、制約を入れないと無限に解がある
ラグランジュ関数を最大にする係数ベクトルを探索(微分して0になる点)
・ラグランジュ関数を微分して最適解を求める
元のデータの分散共分散行列の固有値と固有ベクトルが上記の制約付き最適化問題の解となる
分散共分散行列は正定値対象行列⇒固有値は必ず0以上・固有ベクトルは直行
寄与率:第k主成分の分散の全文さんに対する割合(第k主成分が持つ情報量の割合)
累積寄与率:第1-k主成分まで圧縮した際の情報損失量の割合
第1~元次元分の主成分の分散は元のデータの分散と一致
(2次元のデータを2次元の主成分で表示したとき、固有値の和と元のデータの分散が一致)
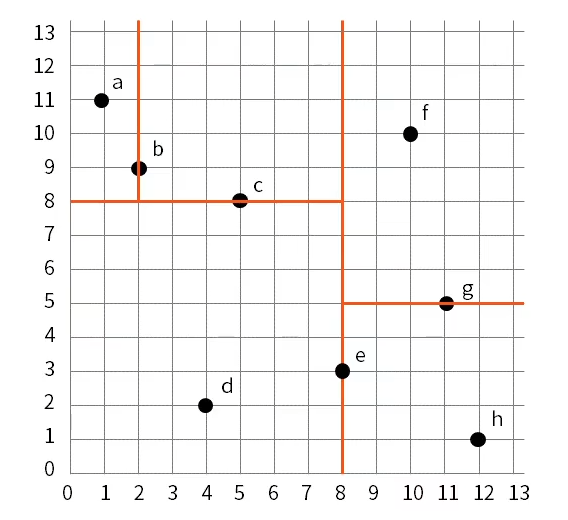
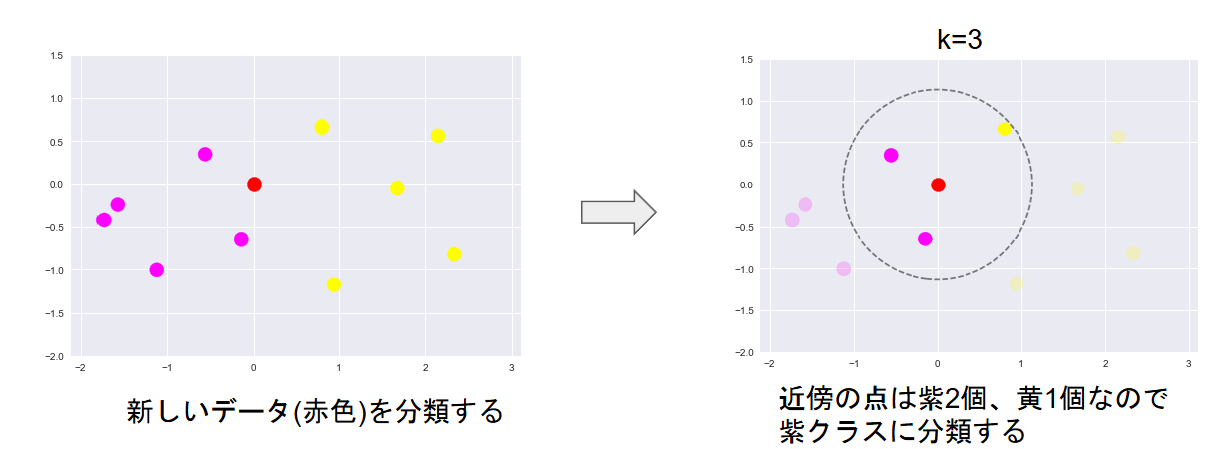
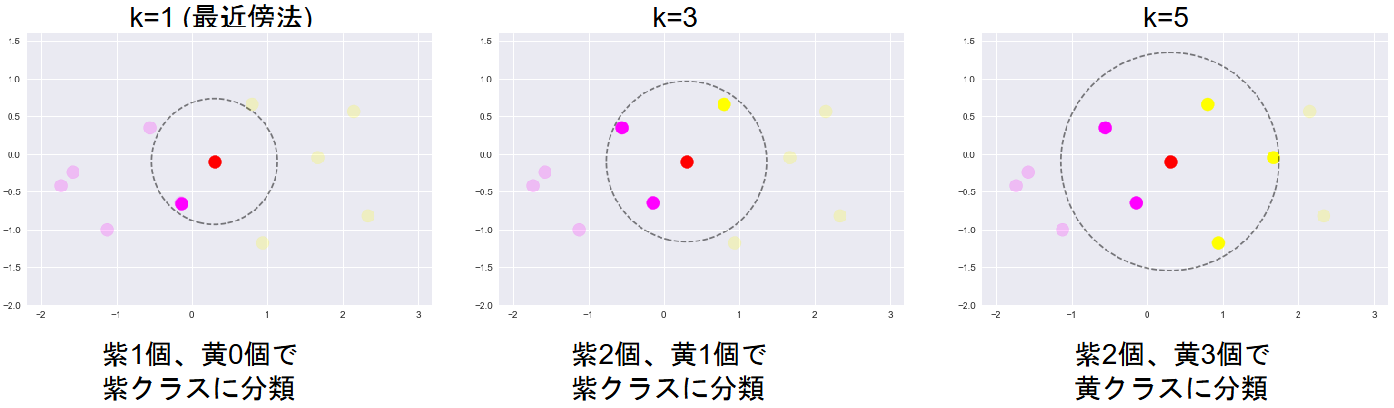
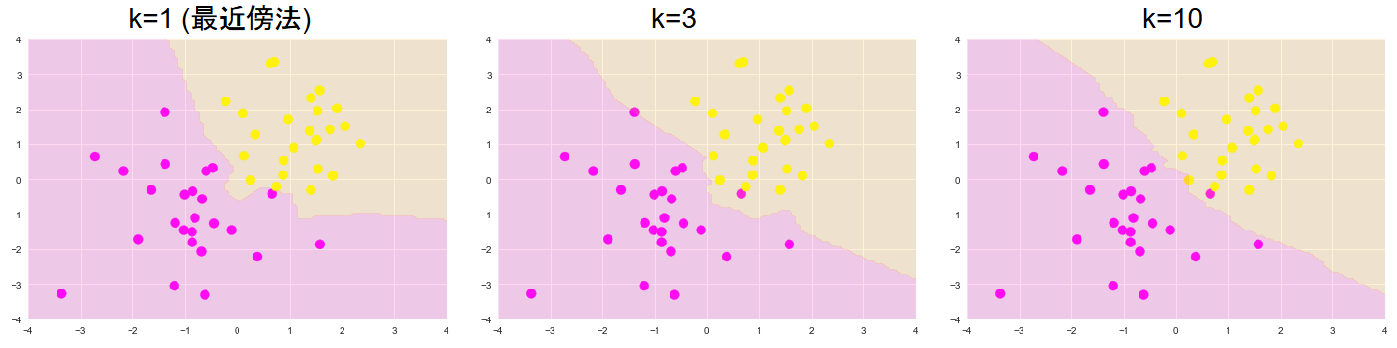
K近傍法:分類問題のために機械学習手法の一つ、最近傍のデータをk個とってきて、それが最も多く所属するクラスに識別
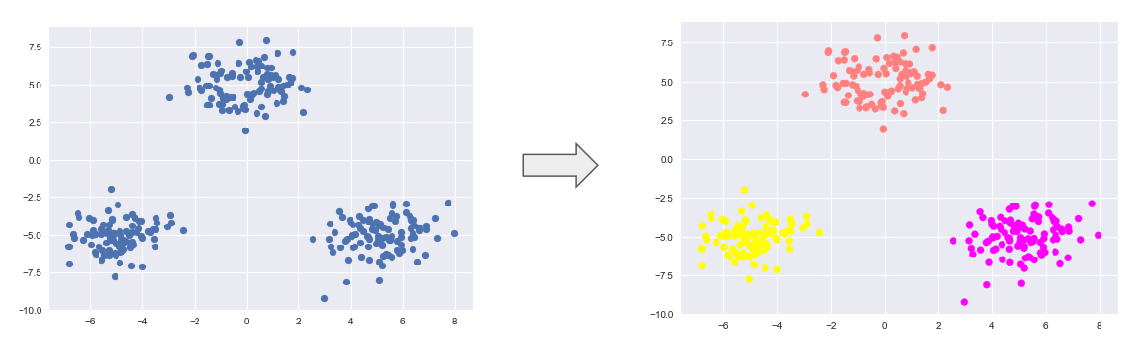
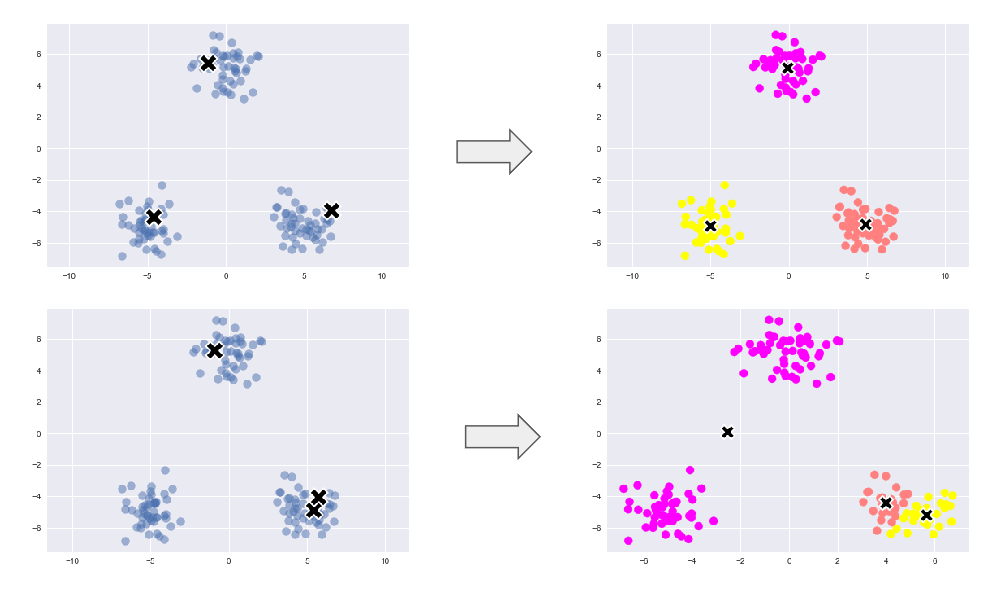
k means:教師なし学習, クラスタリング手法で与えられたデータをk個のクラスタに分類する
中心の初期値を変えるとクラスタリング結果も変わりうる
初期値が離れる⇒うまくクラスタリングできる
初期値が近い⇒うまくクラスタリングできない
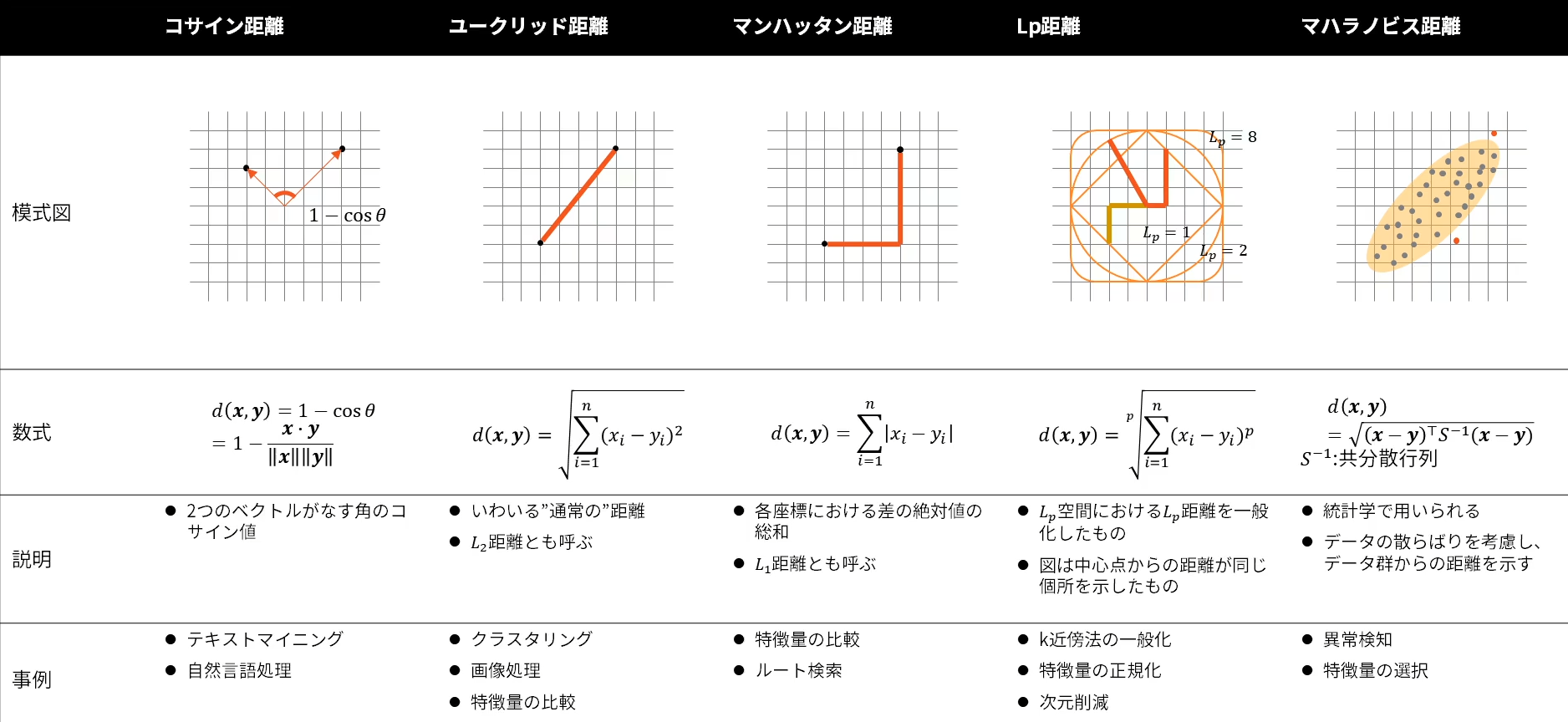
6.パターン認識
K近傍法とその計算に用いられる距離計算方法と性質を理解し、データの特性にあった距離の選択を行う
近似最近傍探索:探索したいサンプルから最も近いものを厳密に計算せず、近似的に距離が近いものを取得する手法
アプローチ:Tree/Partitioning, Graph探索, LSH;局所鋭敏性ハッシュ
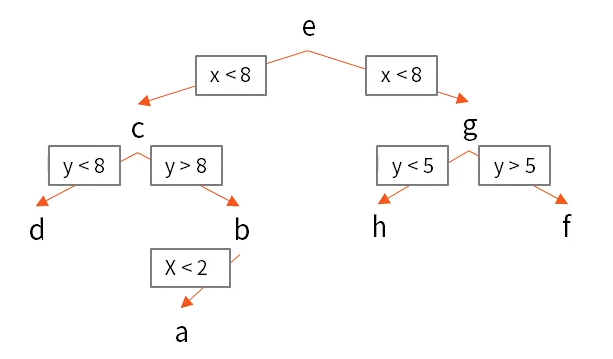
kd-tree(kd木)
多次元空間内のデータを効率的に探索するためのデータ構造、類似するデータを高速に探索、高次元データには適さない