Macで簡単！Pythonを用いた単位ステップ応答のプロット

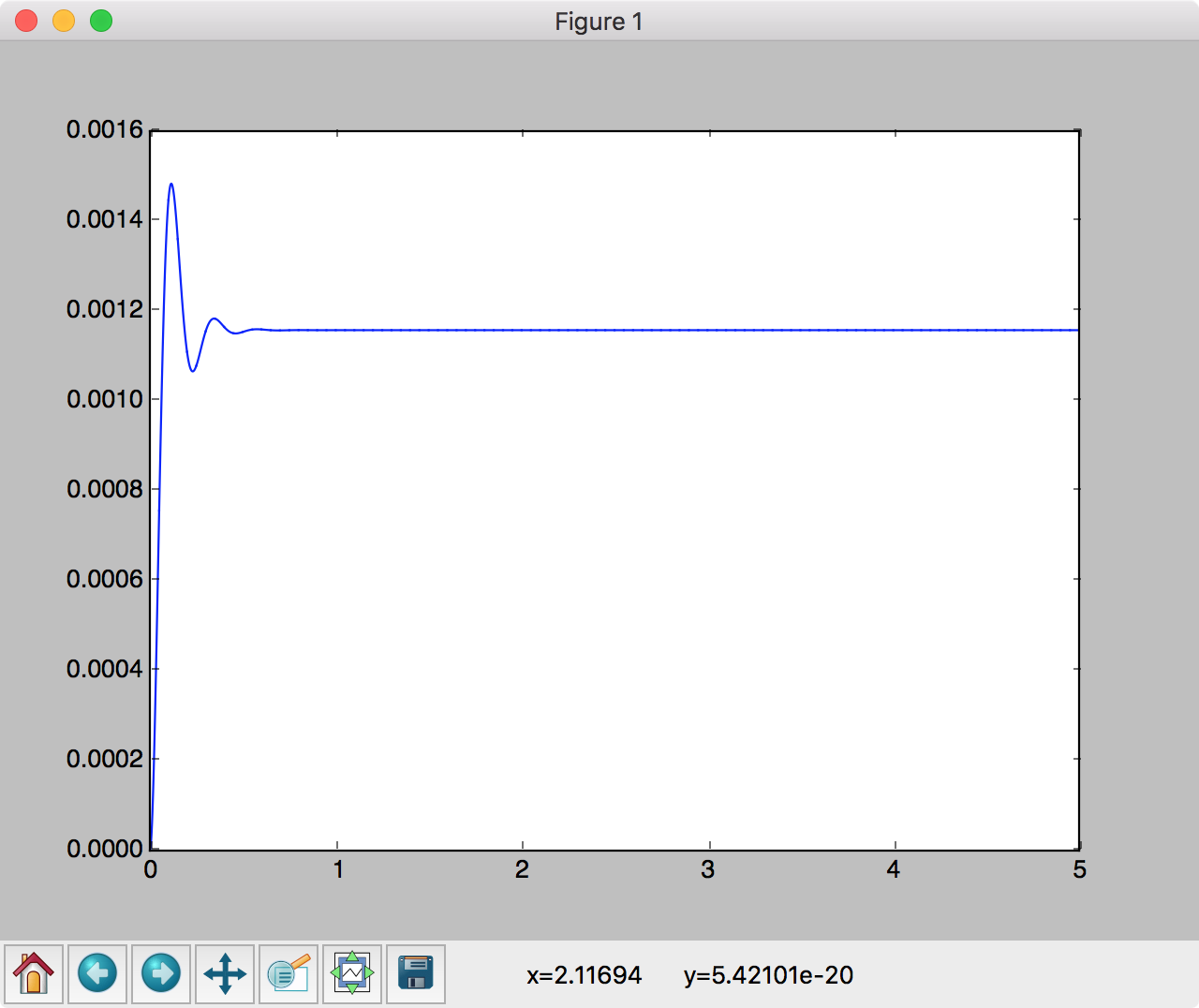
制御を勉強したことのある人であればおなじみの 単位ステップ応答 を実際にプログラムに計算させてグラフに出力してみたいと思います。

---

この記事の対象

• 制御分野を勉強されている方
• Pythonを使用したシミュレーションに興味がある方
• Python初心者の方

---

\frac{d^{2}x(t)}{dt^{2}} + \alpha \frac{dx(t)}{dt} + \beta x(t) = u(t)

今回は、上記の微分方程式で示されるシステムに関してプログラムを作成していこうと思います。
このような数学モデルでは計算が複雑で面倒なので、制御分野ではラプラス変換を用いて時間領域から周波数領域に変換してから計算をします。ですが、コンピュータに計算させてしまえば一瞬で導き出してくれちゃいます。

1.Macを選んだあなたは正解！

Mac（OS X/macOS）には標準でPythonがインストールされています。古すぎる場合などはアップデートが必要なことがありますが、ここでは省略させていただきます。

2.必要なパッケージをインストール

Pythonでは、pipというパッケージ管理システムを利用します。ここでインストールしたパッケージは、importといった感じでプログラム側から読み込んで使用することができるようになります。もし、バージョンアップするように言われたらpip install --upgrade pipを実行しましましょう。

$ pip install numpy
Requirement already satisfied: numpy in /usr/local/lib/python2.7/site-packages

$ pip install scipy
Collecting scipy
  Downloading ..... (21.8MB)
.....
Installing collected packages: scipy
Successfully installed scipy-0.18.1

$ pip install matplotlib
Collecting matplotlib
  Downloading ..... (11.2MB)
.....
Installing collected packages: ..... pytz, pyparsing, matplotlib
Successfully installed ..... pytz-2016.7 six-1.10.0

3.プログラミング

お好きなエディタで以下のプログラムを記述し、拡張子pyで保存してください。

sample.py

from scipy.integrate import odeint
from math import *
import numpy
import matplotlib.pyplot as plot

# 変更してみましょう
alpha = 17
beta = 777

def derivative(x, t):
    dx = [ x[1], - beta * x[0] - alpha * x[1] + 1.0 ]
    return dx

x_init = [0.0, 0.0]
time = numpy.linspace(0.0, 5.0, 10000)
x = odeint(derivative, x_init, time)

# 出力部分
plot.figure()
plot.plot(time, x[:, 0])
plot.show()

4.実行

pythonに引数としてプログラムファイル名を渡してあげると、実行されます。

$ ls
sample.py

$ python sample.py