ARC176 A-01 Matrix again
ARC176のA問題を乱択解法でACしたので、その解法に至った経緯を別解として解説しようと思います。
問題の概要
$N \times N$のマス目があり、そのうちの$M$マスが指定されています。各行各列から$M$個ずつ、指定された$M$マスを含めた$N \times M$マスの選び方を1つ示すという問題です。ただし、$N \le 10^5, M \le \min(N, 10)$を満たします。
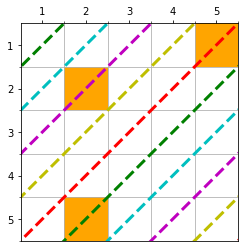
入力例1の場合、$N = 4, M = 2$で、以下のオレンジのマス$(1, 4)$と$(3, 2)$が指定されたマスです。
出力例1で選んだマスは、青マスを含む8マスで、確かに各行各列が2マスずつ選ばれています。
想定解法
いわゆる構築系に属する問題で、複数通りの解答がある中で、いかにシンプルで実装しやすい解を構築するかを考える発想力が問われるタイプの問題です。
その中でも想定解法は、解説が2行で終わるほどシンプルで美しい解法だったので、そちらを先に解説します。
$N \times N$のマス目を、$(x + y)\mod N$が同じものでグループ分けします。つまり、各マスで右上から左下に線を引き、同じ線にのっているマスで分けています。このとき、同じグループに入っているマスを全て選ぶことで、各行各列1マスずつ選択することができます。よって、$N$個のグループのうち、$M$グループを選ぶと各行各列$M$個選択したことになります。
指定されたマスが選択されているという条件があるため、$M$個のグループのうちで、指定マスを含むグループを含むものを選ぶことで、全ての条件をみたすことができます。指定マスの属するグループ被ることあるので、その場合は追加でグループを選ぶことで、同じように条件を満たすことができます。
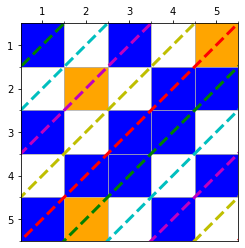
例えば、$N=5, M=3$で、以下の左のような入力では、右図のようにマスを5つの色のグループに分けます。
指定マスを含む赤、紫、緑の線のマスを選ぶことで、条件を満たすことができます。
自分の解法
ここからは、自分がコンテスト中に考えた別解となります。
自分はまず制約に注目しました。$N$が非常に大きくなる割に、指定マスの個数$M$は最大でも10個までという制約です。このことから、指定マスに関わる行や列は少なく、大半は他の制約を受けない無関係な行であることに注目しました。
そこで、指定マスとして登場した行とそうでない行に分けて独立に解くことで、簡単に実装する方法を思いつきました。
指定マスで登場した行や列については、指定マスが$(a_1, b_1), \cdots, (a_M, b_M)$である場合、$ \{ (a_i, b_j) | 1 \le i,j \le M \} $を満たすマスを選ぶことで、指定されたマスを含みながら、各行・列について$M$マスずつ選ぶことができます。$a_i$や$b_j$に被りがある場合は、個数が$M$個になるよう適当に値を追加します。
登場していない行や列については、登場していない行を$c_1, \cdots ,c_{N-M}$、列を$d_1, \cdots, d_{N-M}$として、$\{ (c_i, d_j) | (i-j) \equiv k\mod N-M, 1 \le k \le M\}$を満たすマスを選ぶことで、各行・列について$M$マスずつ選ぶことができます。
例えば、$N = 15, M=5$の場合を図にすると
このようになり、青マスのインデックスを出力することで、全ての条件を満たすことができます。
関係する部分は正方形、関係ない部分は想定解法と同じような斜めに配置する解法になります。この解法は、適切に実装することで$O(NM)$で答えを求めることができます。
解法の欠陥
上記の解法は、$1 \le N \le 10^5, 1 \le M \le \min(N, 10)$の制約の大部分でACすることができますが、一部のケースでは正しく答えが出力されません。
具体的には、$N < 2M$となるケースです。これらのケースは、ビジュアルで考える場合は、右下の領域において、斜めに配置する作戦が破綻します。式で解釈する場合、$(i-j) \equiv k\mod N-M, 1 \le k \le M$の部分において、相異なる$(i, j)$が得られることを前提にしているため、この解法が破綻すると考えることができます。
解決策
コンテスト本番では、この解法を思いついてから20分ほど格闘しました。以下では、最終的にたどり着いてACを取れた解法を説明します。
最終解法では、$(i)N \ge 2M$と$(ii) N < 2M$に場合分けして解きました。$(i)$は最初に思いついた解法で解くことができます。$(ii)$の場合は乱択解法を用いて解きます。
具体的には、$(1,2,\cdots, N)$の順列である$(c_1, c_2,\cdots,c_N)$を作り、$S = \{(c_i, j)| (i-j) \equiv k \mod N, 1 \le i, j \le N, 1\le k \le M \}$を満たすマスを選択する。
このとき、$S$が指定マス$(a_1,b_1), \cdots ,(a_M, b_M)$を全て含む場合、これを出力する。そうでない場合は、順列$c_i$を作り直す。
この、$c_i$を作る操作をランダムで行い、当たりを引くことができるまで繰り返すという解法です。
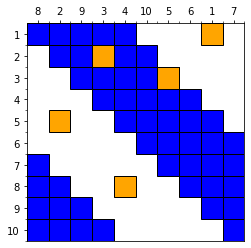
例えば、$N= 10, M=5$で指定マスが$(1, 1), (3, 2), (2, 5), (4, 8), (5, 3)$
下図のように、横軸のインデックスをシャッフルし、指定マスが青色の範囲に全て入るパターンを引き当てた場合は、青マスに該当する座標を答えとして出力すれば正解することができます。
この解法はpypy3で、コンテスト中にACすることができました(1025 ms)。
乱択解法が正解できる確率
まず、全探索ではなく、乱択解法を用いた理由を説明します。
場合分けの制約から$N < 2M \le 20$であることが分かります。この解法では、単純に長さ$N$の順列を全探索する必要あるので、計算量オーダーは最大で$19! \sim 10^{16}$となり、全ての順列を考えるのは不可能です。しかし、その中でも当たりの順列は無数にあるはずなので、ランダムに順列を探索する解法を用いることにしました。
それでは、乱択解法が正答できる確率を考えてみます。
まず、1回の順列$c_i$の抽選で当たる確率を考えてみましょう。もっとも当たりの確率が小さくなる場合は、指定マスが$(1, 1), (1, 2), \cdots (1, M)$のように、同じ行や列に固まっている場合で、選択されないマスの割合がもっとも大きくなる$N= 19, M= 10$の場合になります。
当たりの条件は、$c_1$から$c_{10}$が$1~10$の順列になっていることで、その確率は、$1 / _{10}C_{19} = 1 / 92378$となります。
よって、1つのテストケースに正答できる確率は、乱択のループの回数を$r$とすると、$1 - (1 - p)^r$で計算できます。ここから、1つのテストケースにある確率で正解するために必要なループ回数を計算できます。
| $1 - (1 - p) ^ r$ | $r$ |
|---|---|
| 99% | 425415 |
| 90% | 212708 |
| 80% | 148676 |
| 70% | 111220 |
| 60% | 84645 |
| 50% | 64032 |
| 40% | 47189 |
この解法を撃墜するために複数のテストケースがある場合や、Hackがあるタイプのコンテストの事を考慮すると、9割程度の正答率がないと適切な解法とは呼べないでしょう。
ACコードのループ回数
それでは、ACしたコードが実際に何回ループを回せたか確認します。コードにカウントするための変数を追加し、制限時間2sの限界まで回るよう書き直しました。
Pypy3で回した結果、ループ回数は平均で61000回でした。
このとき、もっとも都合の悪いテストケースで正答できる確率は約48%です。
よって今回の乱択解法は、とんだ嘘解法であることがわかりました。
ACした理由の考察
ACした理由は単純で、この解法を撃墜するようなテストケースが含まれていませんでした。テストケースを調べたところ、$N < 2M$に場合分けされるテストケースは、最もサイズが大きいケースでも$N = 10, M = 10$であったので、乱択解法が仕事したテストケースは見受けられませんでした。
まとめ
今回、思いついた乱択解法は想定された場合、撃墜される可能性が高く、ラッキーACであることが分かりました。ただし、コンテスト本番では「ACが正義」なので、可能性を感じる解法なら提出してみてみましょう。