はじめに
この記事では、総当たり戦の途中経過から各チームの順位確率(どの順位で終了するか)の確率を計算するプログラムについて解説しようと思います。今回はゲームスポーツのプロリーグを使って計算します。
総当たり戦(リーグ戦)
総当たり戦の説明です。ご存じの方は飛ばしてください
総当たり戦とは、競技大会の試合形式の一つで、全ての参加者と1回ずつ試合を行い、その試合結果から順位を決めるという形式です。プロ野球のペナントレースや、サッカーのJリーグ、予選としてのグループリーグとして多くの場面で採用されている形式です。
総当たり戦のメリットとして、全ての相手と対戦するので、相性よりも総合的な実力が反映されやすく、トーナメント戦と異なり、優勝者だけでなく全ての参加者の順位を決めることができるので、下部リーグと入れ替わるチームを決めたりすることができます。
一方で、デメリットとして、試合数が多くなることがあげられます。全ての相手と1回対戦する形式(いわゆるシングルラウンドロビン)を$n$チームで行うと、${}_n C_2 \approx n^2$試合することになり、参加者が増えると試合数がとても多くなります。また、最終節の試合では優勝チームが確定していることが多く、消化試合が発生しやすいというデメリットもあります。
Rainbow Six Siegeのプロリーグについて
最近は、Eスポーツという言葉をよく聞くようになり、今年の4月に「VALORANT」の世界大会で、日本チームの「ZETA DIVISION」が世界3位になり話題になりました。この総当たり戦形式は、他のプロスポーツと同様に、ゲームスポーツ(Eスポーツ)でも多くの場面で採用されています。
今回、順位確率を計算するにあたり、その題材として「Rainbow Six Siege」というゲームのプロリーグを使ってみようと思います。これを選んだ理由としては、順位決めのやり方がある程度複雑でありながら、確率を考えやすいゲームだったので選びました1。もう一つの理由としては、最近日本チームがアツいということもあります2。
このゲームや、プロリーグに関しては以下を参照してください。
この記事は以下の勝ち点の決め方や順位決めについてを知っておけば読めるようになっています。
今回は日本チームが参加している北部アジアリーグ「APAC North division」で計算しようと思います。
リーグの概要は以下のようになっています。
- 8チームによるBO1(1マップ先取)の総当たり戦。全チーム1回ずつ対戦する。(いわゆる、シングルラウンドロビン)。
- 1マップは12ラウンドの7ラウンド先取、6-6になった場合は延長戦(オーバータイム)で8ラウンドに到達した方が勝ち。引きわけはありません。
- 勝ち点は
延長なしのとき:勝ち 3点、負け 0点
延長ありのとき:勝ち 2点、負け 1点
→全試合28試合で、合計勝ち点84点を8チームで取り合うという感じです。 - 勝ち点が同じ時は、「同勝ち点のチームの勝敗」→「得失点ラウンド」→「勝数」→「取得ラウンド率」→「タイブレークマッチ」の順に優先して順位を決めます。
余談ですが、このAPACリーグでは上位2チームがMajorという世界大会のイスを争っているので、特にここに滑り込めるかが重要になってきます。このプログラムを作った経緯として、日本チームがどれくらいの確率でMajorに出場できるのか気になったため、このようなものを作りました。
参加チーム
- 日本チーム
- CYCLPS athlete gaming
- FAV gaming
- Fnatic
- REJECT
- 韓国チーム
- SANDBOX Gaming
- DAMWON Gaming
- Talon Esports
- Spear Gaming
Day4(2022/10/05時点)までの結果。liquipediaより引用。
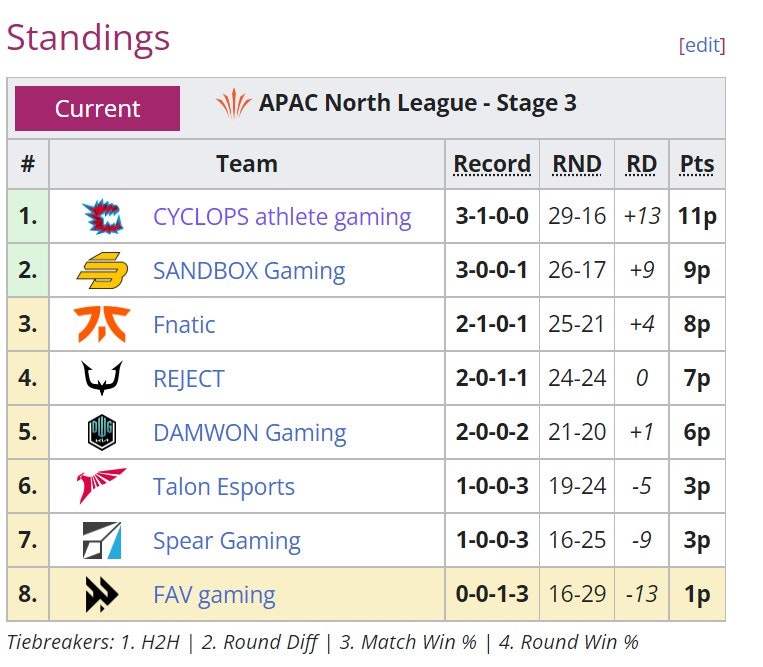
現在のランキング。Ptsが勝ち点

全体の試合結果。取得ラウンド数が載っています。
計算の方針
この時点で行ってない試合は12試合あります。当然、全ての試合の結果を考えて確率を電卓でポチポチ計算するのは現実的ではないので、コンピューターの力を借りることになります。
まずは力業で、コンピューターで全ての試合の結果をシミュレートすることで確率を計算することを考えてみようと思います。その際に、試合結果をどこまでシミュレートするかを考えましょう。順位決めに関係する情報だけシミュレートすればいいので、今回は試合終了時のラウンドスコアをシミュレートできれば完璧に確率を計算することができます。
試合結果は、7-0~5,8-6,8-7と勝敗が逆のパターンで全部で16通りあります。残試合12試合分がこれらの結果を取り得るので、全てシミュレートすると$16^{12} \approx 2.8 \times 10^{14}$通りで、これらを全てシミュレートすると、軽く数時間かかると思うので、他の方法を考えた方がよさそうです。
そこで、今回は全てを計算することは諦めて、妥協案としてモンテカルト法を用いて、近似値を求めてみようと思います。(もしかしたら、効率よく全てのパターンを計算するアルゴリズムがあるのかもしれないですが、分からなかったので妥協しました。)
実装
まず、シミュレーションを始める前に、試合の結果から順位を決めるプログラムを作ります。
順位は取得ラウンドの情報があれば、勝利数や勝ち点が分かるので、タイブレークマッチ以外の順位判定を行うことができます。
import numpy as np
import random
# チーム数
N = 8
# 参加チーム
Teams = [
"SANDBOX Gaming",# 旧Cloud9
"CYCLPS athlete gaming",#(CAG)
"FAV gaming",
"REJECT",
"DAMWON gaming",#(DWG)
"Talon Esports",
"Spear Gaming",# 旧 T1
"Fnatic"# 旧 Guts Gaming
]
# 取得ラウンドのテーブル(stage3 Day4 22/10/05終了時点)
# まだ戦ってない試合には-1,同じチームがクロスするところには0
result = np.array([
[ 0, -1, 7, 5, -1, 7, 7, -1], #SAND
[-1, 0, 7, 8, 7, 7, -1, -1], #CAG
[ 3, 3, 0, -1, -1, -1, 4, 6], #FAV
[ 7, 6, -1, 0, 7, -1, -1, 4], #REJECT
[-1, 3, -1, 4, 0, 7, -1, 7], #DWG
[ 5, 4, -1, -1, 3, 0, 7, -1], #Talon
[ 2, -1, 7, -1, -1, 3, 0, 4], #Spear
[-1, -1, 8, 7, 3, -1, 7, 0], #Fnatic
])
# 順位を判定する
def get_standings(result, tiebreak):
points = [0] * N # 勝ち点
wins = [0] * N # 勝利数
#勝ち点、勝数の計算
for i in range(N-1):
for j in range(i+1, N):
# i:チーム A vs. j:チーム B
if result[i][j] == -1: # まだ対戦していないとき
continue
u = result[i][j] # チームA取得ラウンド数
v = result[j][i] # チームB取得ラウンド数
# チームAが勝ったとき
if u > v:
wins[i] += 1
#両チームの勝ち点は、勝利チームのラウンド数が7のとき3-0,8のとき2-1
points[i] += 10 - u
points[j] += u - 7
# チームBが勝ったとき
else:
wins[j] += 1
points[j] += 10 - v
points[i] += v - 7
#同勝ち点の勝ち数(H2H tiebreaker)
H2Hwins = [0] * N # 直接対決の勝利数
for i in range(N-1):
for j in range(i+1, N):
# i:チーム A vs. j:チーム Bで勝ち点が同じチーム同士の対戦について勝利数をカウントする
if points[i] != points[j] or result[i] == -1:
continue
u = result[i][j] # チームA取得ラウンド数
v = result[j][i] # チームB取得ラウンド数
if u > v:
H2Hwins[i] += 1
else:
H2Hwins[j] += 1
# 試合結果をまとめて順位を判定する
standings = []
for i in range(N):
# 得ラウンド数は横方向に和をとる
# 失ラウンド数は縦方向に和をとる
# maxを入れて-1を0にしておく
round_win = np.sum(np.max(result[i], 0))
round_lost = np.sum(np.max(result[:, i], 0))
# 得失ラウンド差
round_diff = np.sum(table[i]) - np.sum(table[:, i])
# (チーム番号, 勝ち点, 直接対決の勝利数, 得失ラウンド差, 勝利数(勝率), 取得ラウンド率, 順位決定戦(後述))
standings.append((i, points[i], H2Hwins[i], round_diff, wins[i], round_win/(round_win+round_lost), random.random()))
# より左の項目を優先して大きい順にソート
standings = sorted(standings, key = lambda x: (-x[1], -x[2], -x[3], -x[4], -x[5], x[6]))
return standings
実際のタイブレークのルールでは、得失ラウンド差の次は勝率を比較しますが、大会の進行にイレギュラーがない限りは、全チーム7試合行い、また、引き分けも発生しないので、勝利数を比較すれば良いです。また、Northでは、各節で全てのチームが1試合ずつするようにスケジュールが決まっているので、途中経過であっての勝率は勝利数と同じと見なすことができます。
モンテカルロシミュレーション
ここから、順位確率の計算について考えていきます。
まず、モンテカルロ法をについて軽く説明しておきます。
モンテカルロ法とは乱数を用いた試行を繰り返すことによって、近似的に確率を計算する数値計算の手法です。平面上に大量の点を打って、円の内側と外側の点の比率から円周率を求めるといった使い方が有名だと思います。
順位確率の計算においては、まだ試合を行っていない部分をランダムに埋めるという試行を何度も行います。すべての試合の結果が埋まっている対戦表が大量にできるので、それぞれについて順位を決定して、試行のうち何回1位になったかを計算すれば、そのチームが1位になる確率が計算できます。他の順位でも同じように計算していくことで、全てのチームが最終的にどの順位になるかという確率を計算できます。
次に、試合結果をランダムに生成する方法について考えてみようと思います。順位を判定するときにも述べたとおり、各対戦の取得ラウンド数が決まればよいので、「試合結果」=「何対何で決着したか」と考えれば良いです。
実際の対戦では、実力差や戦術の相性、試合マップ、攻守の得意不得意などによって、どちらが勝ちやすいとか延長戦になりやすいといった、確率の偏りのようなものがあるとは思います。しかし、それらを考慮すると、またしても多くの場合分けが必要になってきます。そのため、今回は全てのチームの実力はほとんど同じで、対戦相手にかかわらずラウンドを取得できる確率は1/2であるという仮定を置いて計算します。
つまり、コイン投げでラウンドの結果を決めるということになります。そのため、試合結果を生成するには、コインを最大15回なげて、どちらかの面が先に7回(8回)出たら試合終了として、表裏の出た回数をその試合の取得ラウンド数とすることができます。対戦の結果は、全部で16通りありますが、数Aで習う反復試行の確率を使えばどの結果が何%で出るかを計算することができます。
pythonでは、指定した確率分布で乱数を生成することもできますが、計算するのが面倒なので、あらかじめコインを15回投げておいて、上と同じように表裏の順番からラウンド数を決定します。例えば、「裏表裏裏裏表表裏表裏裏表表表表」であったときは、チームA 4-7 チームBという結果になります。よって、「試合結果」=「コインを15回投げた結果」になりました。
ただし、実装では$0$~$2^{15}$の一様乱数を生成して、それを15桁の2進数表記に変換して、頭の桁からみて、0なら表、1なら裏というようにして、コイン投げの結果をランダムに生成しています。
def randomscore():
# 0から2^15の一様乱数を生成して、15桁の2進数に変換
b = format(random.randint(0, 1 << 15), "015b")
u = 0 # チームAの取得ラウンド
v = 0 # チームBの取得ラウンド
# 0ならチームA,1ならチームBが勝ち
for j in range(15):
if b[j] == "0":
u += 1
else:
v += 1
if j < 12:
if max(u, v) == 7:
return u, v
elif max(u, v) == 8: # 6-6になって延長戦になったとき
return u, v
この乱数に基づいて、対戦表を埋めていき順位を判定しますが、このままでは不十分なところがあります。勝ち点が同じだった場合でも、他の4つの項目で優劣を決めることになっていますが、それでも同じ場合は順位決定戦(タイブレークマッチ)を行います3。そこで、順位判定の際に全てのチームに乱数をふっておいて、万が一タイブレークマッチが発生した場合は、その乱数の値が小さい方が勝ちというようにします。
このようにして、大量の順位表を生成して、それぞれのチームについてどの順位に何回なったかをカウントします。最後に順位表を作った回数で割り算すると、順位確率の表を作ることができます。
試行回数については、多ければ多いほど精度が上がりますが、その分計算時間が延びるので、いい感じの回数で区切りましょう。
# それぞれのチームがどの順位になったかをカウント
count = np.zeros((N, N))
# 試行回数
l = 100000
#残りの試合を調べる
remaing_match = []
for i in range(N-1):
for j in range(i+1, N):
if table[i][j] == -1:
remaing_match.append((i, j))
# シミュレーション
for _ in range(l):
newtable = np.array(table)
# 残りの試合について、ランダムに試合結果を生成すして、対戦表を埋めていく
for i, j in remaing_match: # チーム i vs. チーム j について
p, q = randomscore()
newtable[i][j] = p
newtable[j][i] = q
# 順位判定をして、1位から順に足し込んでいく
standings = get_standings(newtable)
for i in range(N):
team_num = standings[i][0] # (i+1)位のチーム番号
count[team_num][i] += 1
# 試行回数で割って、パーセントに直す
prob = count / l * 100
細かく分けてせつめいしましたが、ここまでのコードをつなげると順位確率を計算できます。
結果
順位確率を現在順位が高い順に表示します。すべてパーセントで表示しています。
1st 2nd 3rd 4th 5th 6th 7th 8th
55.1 25.3 11.4 6.1 2.0 0.1 0.0 0.0 CYCLPS athlete gaming
23.7 27.1 19.8 15.9 11.2 2.2 0.2 0.0 SANDBOX Gaming
16.3 22.8 21.1 19.0 12.9 6.3 1.5 0.0 Fnatic
3.1 14.3 24.1 21.9 18.1 9.5 6.7 2.3 REJECT
1.9 9.9 15.7 20.6 24.8 14.9 8.9 3.3 DAMWON gaming
0.0 0.3 3.8 7.0 12.7 29.6 24.6 22.0 Talon Esports
0.0 0.3 3.8 6.9 12.8 23.9 35.6 16.7 Spear Gaming
0.0 0.0 0.3 2.6 5.4 13.6 22.6 55.5 FAV gaming
試行回数は100000回で計算すると、計算時間はおよそ40秒ほどでした。四捨五入して表示しているので、各行や列の和が100%にならない場合があります。
また、この表を見るときの注意として、0.0となっていても、「$=0$%」の場合と、「$\fallingdotseq0.0$%」場合があります。例えば、この結果で言うと、一位のCAGが7位まで落ちることはないとは限りません。(今回の場合は、残りの試合がどんなに都合の悪い結果でも7位にならないことは確認できます)。100.0の場合でも同様のことが言えるので、「プレーオフ確定」や「残留確定」といった確認は、勝ち点の差や残った試合の組み合わせなどから、個別でやらないといけない場合があります。
順位確率を見てみましょう。現在トップのCAGは、およそ80%の確率でTOP2に入ることができそうです。一方で下位3チームは、TOP2に入る確率は1%未満なのでかなり厳しそうです。
また、各チームで確率が最大になる順位を見てみると、Fnatic(現在3位)とREJECT(現在4位)は、ともに3位になる確率がもっとも高くなっています。また、8位になる確率は、Talon Esports(現在6位)とSpear Gaming(現在7位)を比べると、順位が高いTalonの方が大きくなっています。(おそらく、SpearはFavに既に勝っているためと思われます。)
確率が入り乱れている様子を見ても、ある程度もつれているリーグであることが分かります。
まとめ
このように順位確率を計算することができました。リーグ戦のとしては、折り返しを過ぎたばかりですが、トップが走っているという状況ではないので、計算結果もそれなりに面白くなりました。
順位確率というのは、計算している側からしたら完全に趣味なのですが、今シーズンのプロ野球のように、最終戦まで分からないようなリーグがあれば、確率を計算するとおもしろいかもしれません。