はじめに
栗林公園(りつりんこうえん)は、香川県高松市にある特別名勝に指定された庭園で、文化財庭園としては日本で最大の庭園です。江戸時代初期から100年以上の時間をかけて造園され、その約75ヘクタールという広大な敷地には、6つの池と13の築山が巧みに配置され、四季折々の美しい景色が楽しめます。庭園内を歩きながら、風情ある茶室や松の木、借景の紫雲山などを眺めることができ、国内外から多くの観光客が訪れる名所です。
その景色は回遊式庭園として非常に多様な表情を見ることができ、私の友人も「任意の景色がいい」というコメントを残したほどです。事実、その景色は比喩として「一歩一景の美しさ」と表現され、歩みを進めるごとに目に映る景色が美しく変わると言われるほど、さまざまな角度からその表情に富んだ景色を目にすることができます。
栗林公園の中は見学の順路というものが設定されておらず、比較的幅の広めの道で構成されているため、観光客はその時の気分に応じて自由な順路で観光することができます。反対に日本で最大の面積を誇る庭園というだけあって、迷子になるほどではないですが、分かれ道が非常に多く、どの順番で観光するか迷う方も多いと思います。
栗林公園の公式ウェブサイトでは、「短時間」で観光したい人向けに、60分/90分で主要ポイントを周回するモデルコースが紹介されています。高松市へ観光に来た人とっては、高松城址や屋島に本場の讃岐うどんであったり、金刀比羅宮、仏生山温泉、一鶴等々、非常に多くの魅力的なものがあるため、栗林公園を短時間で楽しむことができるモデルコースは非常にありがたいものです。
しかし、紹介されているモデルコースでも、全ての景色を見尽くすことはできないので、今回は栗林公園のすべての全ての景色をできるだけ効率よく楽しむ方法を探し求めていこうと思います。
「全ての景色を楽しむ」について
全ての景色を楽しむには、公園内の歩いて行ける地点をすべて歩いて回る必要があるので、この記事では「全ての景色を見る」= 「歩ける道をすべて通る」と解釈して、園内の道をすべて通ることを目標とします。また、栗林公園には複数の入り口がありますが、車で来ることを想定すると駐車場まで戻ってくる必要があるので、その順路のスタート地点とゴール地点が同じ場所であることを前提とします1。
手法
「最速で巡ろう」の記事の第2弾ですが、前回の「祇園祭を最速で巡ろう」では決められた地点をすべて通る問題であったのに対して、今回は決められた道路をすべて通る問題であり、前回とは本質的に異なる問題です。本記事では、最初にこの節で計算に必要な手順を先に説明してから、実装を示していこうと思います。
今回の問題の本質は、全ての道路を1回以上通る道順のうちで最も距離が短いものを求めるという問題になります。この問題は「中国人郵便配達問題」とも呼ばれます。いきなりこの本質問題から考えるのは難しいので、もう少し簡単な問題から順に考えてみようと思います。
以降では、地図上の「交差点」は3方向以上の行き先がある場所のこと、「道路」は交差点の間を結ぶ道のことを表しています。特に、道路はひとつながりの道であっても、交差点で区切られているものだと考えてください。これらは、それぞれグラフ理論の頂点と辺に対応するものとなっています。
Step1
まずは、「全ての道路を1回だけ通る道順」を考えてみましょう。全ての道を1回だけしか通らないということは、どのような道順を通ったとしても総距離は変わらないので、「最も短い」という要請は無視して考えることができます。この問題は、実はパズルなどでよく登場する一筆書きと全く同じ問題であり、地図の形によってうまくいったりいかなかったりします。一筆書きをした場合は余計な道を通ることがないため、もし与えられた地図が一筆書きできる場合、元の問題の答えも一筆書きの道順と一致します。
しかし、一般的に与えられた地図や図形が一筆書きできるとは限らないので、次は地図が一筆書きできる条件について考えましょう。
これは地図上の道路ではなく、交差点に着目すると簡単に理解できます。一筆書きでは、同じ道路を通ることができないため、ある交差点にたどり着いたら必ず来た道とは別の道を使って、その交差点から離れていくことになります。2回目以降もまだ使ってない道を使って来て離れるというのを繰り返します。よって、交差点に繋がっている道路の数が偶数の場合は、その半分を交差点に来るため、もう半分を交差点から離れるために使うこととなります。一方で、道路の数が奇数の場合は、最後に残る一つは来るための道となりますが、ほかの道路は既に使っているので、その交差点から出ることができなくなります(下図のように青線が一本余ります)。
| 道路の数が偶数の交差点 | 道路の数が奇数の交差点 |
|---|---|
 |
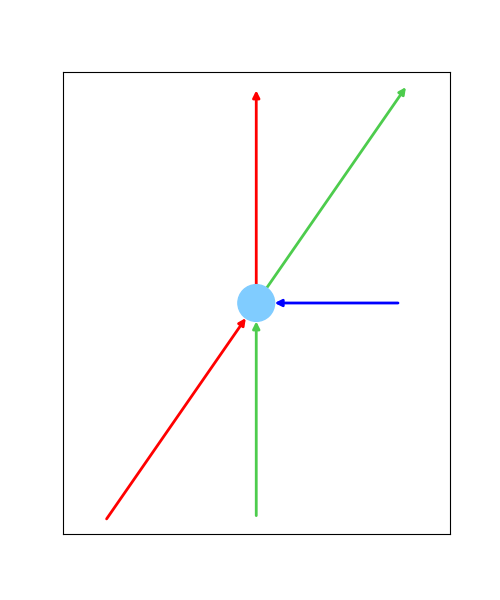 |
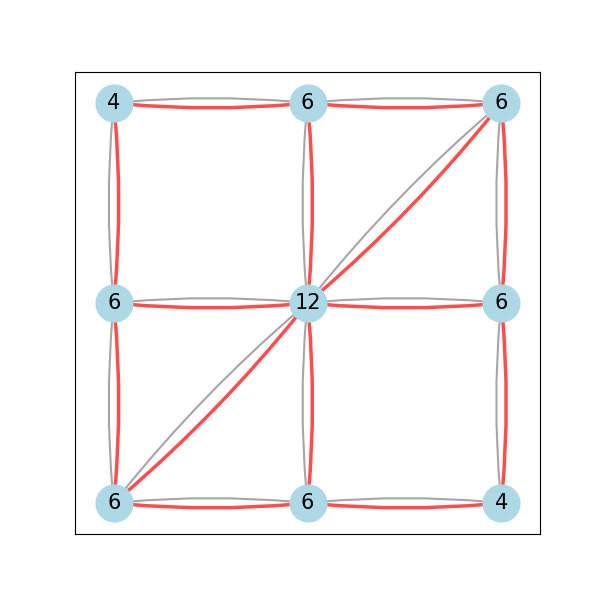
このことから繋がっている道路の本数が奇数の交差点があると、最終的にその交差点から動けなくなるため、これが一筆書きできない地図の条件になります。裏を返すと、一筆書きできる条件は、「全ての交差点の繋がっている道路の本数が偶数本であること」となります2。(下図の丸の数字は、繋がっている道の数を示しています)
| 一筆書きできる(全て偶数) | 一筆書きできない(一部が奇数) |
|---|---|
 |
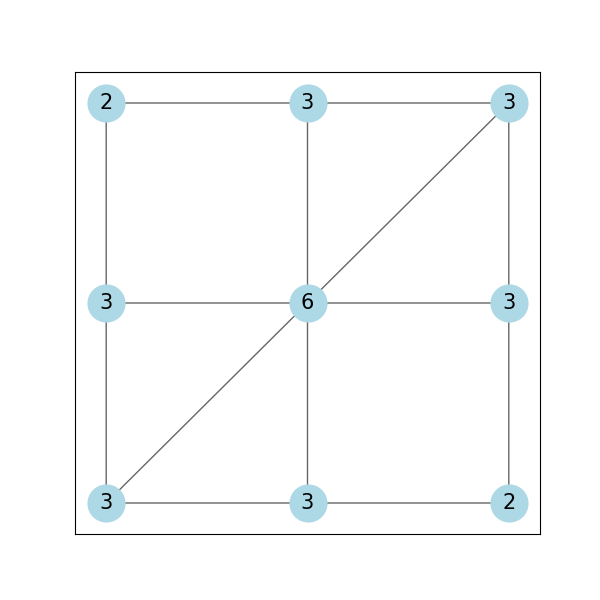 |
Step2
一筆書きできる地図の条件を考えましたが、道路の本数が奇数の交差点といえば丁字路や五叉路なんかが該当します。現実の地図を適当に切り取って考えると、このような交差点がないことというのは、相当シビアな条件であることに気が付くと思うので、次は少し条件を緩くしたような以下の一筆書きを考えてみましょう。
- 全ての道路を1回以上通ること
- 同じ道路を通ることができるのは2回まで
同じ道をもう1回だけ通ることを許容している条件です。ここでも「最も短い」という要請は無視します。
実はこの緩めの一筆書きは、全ての道路がつながっている場合はどんな地図でも一筆書きが可能です。方法は、全ての道路を2回ずつ通るようにすれば、必ずこの一筆書きを達成することができます。考え方としては、「2回通る道路」は「1回だけ通る道路が2本存在する」と解釈すると、全ての道路について仮想的な道路が複製された状態の地図で普通の一筆書きをするのと同じになります。普通の一筆書きはStep1の条件を使うことができて、全ての交差点で道の数が偶数になるということから、この緩めの一筆書きが可能であるとわかります。(Step1で一筆書きできない図も、一筆書きできるようになります。)
このことから、「全ての道路を1回以上通る道順」は少なくとも緩い一筆書きの手順で作ることができるので、その最短移動距離は、全道路の長さの総和の2倍が上限となること分かります。このStep2でのポイントは、「2回通ること」を「仮想的な道路をもう一つ複製する」と考えることによって、2回通ることを許容した場合に、道の数が奇数の交差点をなくすようにすることができることです。
Step3
最後に、Step2の緩めの一筆書きに加えて、「距離が最も短い」という条件について考えてみましょう。
普通の一筆書きをできる地図が存在することを考えると、全ての道路を2回ずつ通るようなルートにすることは明らかに無駄が含まれているため、この無駄をなくすことを考える必要があります。ポイントはStep2と同じく、道路が奇数の交差点をなくすことですが、全ての道路を二重にするのではなく、無駄がないようにいくつかの道路だけを複製してこれを達成したいです。
地図上のある道路を二重にすると、その両端の交差点の道路の本数の偶奇が変わります。繋がっているいくつかの道路を連続で二重にすると、中間にある交差点は偶奇が変化せず、両端の交差点のみ偶奇が変化します。この性質を使うと、2つの繋がっている道路が奇数の交差点の間を二重化すると、その両端の交差点は道路の本数が偶数に変わります。よって奇数の交差点同士のペアを作って、ペアごとにその間の道路だけを二重にすることで、全ての交差点の道路の本数を偶数に変えることができ、例えば下図のようにすれば、一部分を二重にするだけ全て偶数にできます。こうして得られた一部の道路を二重にた地図は、必ず一筆書きが可能です。
よって、「全ての道路を1回以上通る道順」は、「一部の道路を二重にした地図の一筆書き手順」と同じものと見なすことができます。一筆書きの場合は、移動距離の総和は手順に関係なく道路の長さの総和となるので、最短順路を見つけることは『「二重にした地図」の中で道路長の和が小さい地図』を見つけることに等しいです。
道路を二重にした地図の道路長の和は、元の地図と比較すると二重になっている道路の分だけ増加するので、二重になる道路の長さが短くなるようなペアの作り方を見つけることができれば、本質問題の解を求めることができます。
ここまでの説明では、地図の中のいわゆる「行き止まり」について考えなていません。しかし、行き止まりの端を道路が1本繋がっている交差点とみなすことで、同じ議論にのせることが可能になるため、行き止まりを含む場合であっても、ここまでの考え方を適用することができます。また、奇数の交差点が全てペアを作れるようにするには、その数が偶数個である必要がありますが、「握手補題」より奇数次数の交差点は必ず偶数個存在することが証明できます。
実装方針
Step3の考え方を念頭に置いて、大きな計算の流れを説明すると
- 地図上で繋がっている道路が奇数の交差点同士の距離を求める
- ペア間の距離が最も小さくなるようなペアの組み合わせを求める
- ペア間の道路を二重にして、一筆書きの手順を構築する
データ
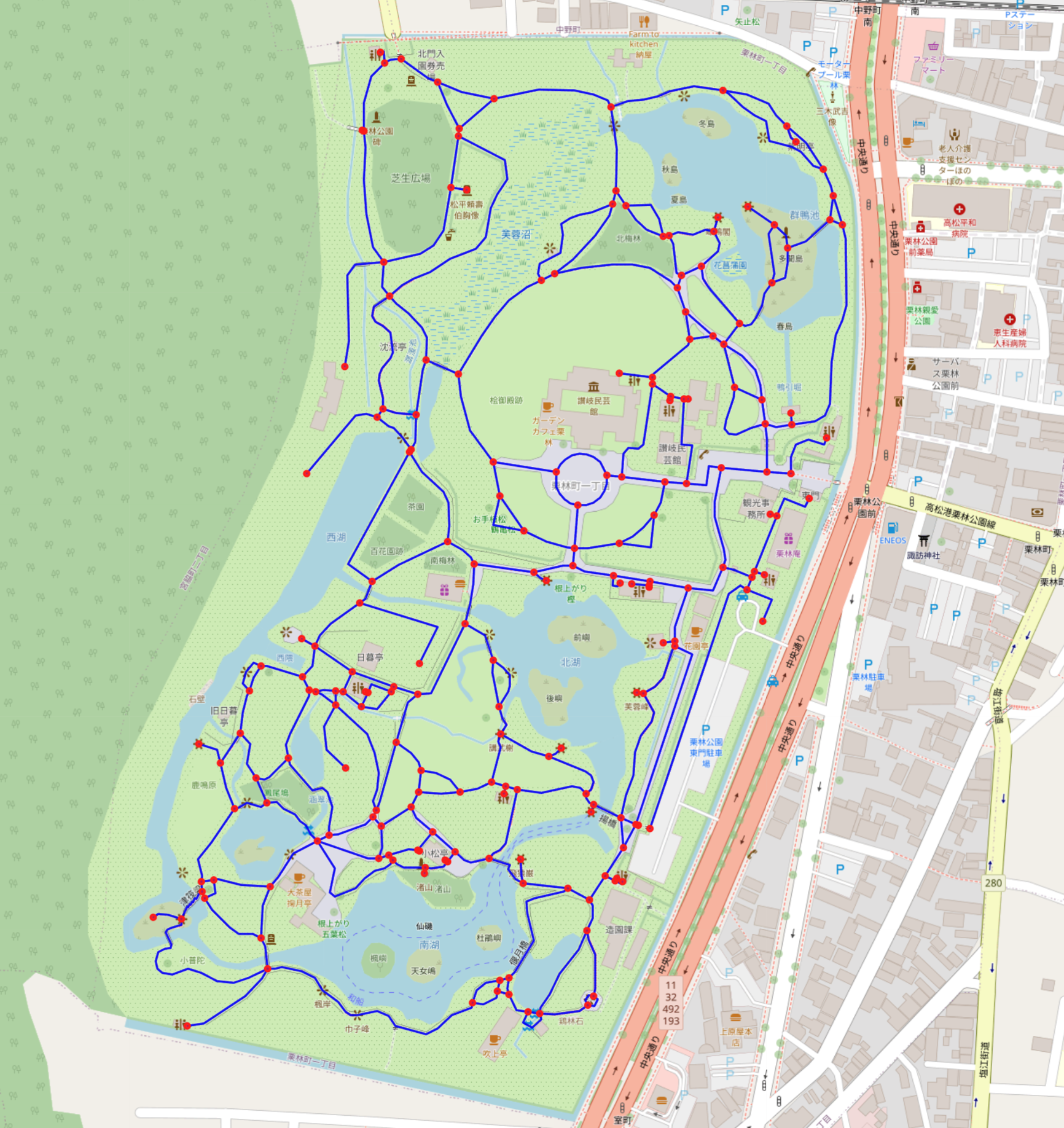
栗林公園内の地図データとして、OpenStreetMapの地図データで栗林公園(Ritsurin Garden)として指定されている範囲の歩道を使用します。
Pythonでは、osmnxというライブラリを用いて、OpenStreetMapの地図データを取得します。地図データはPandasのDataframeと似た形式で、地図の交差点に相当するNodeと道路に相当するEdgeで構成されています。地図の描画には、Foliumというライブラリを使用します。
import osmnx as ox
import folium
import numpy as np
area = 'Ritsurin,Takamatsu,Kagawa,Japan'
# 道路ネットワークの取得
G = ox.graph_from_place(area, network_type="walk")
# グラフのノードとエッジを取得
nodes, edges = ox.graph_to_gdfs(G)
# 地図の初期化(中心座標を計算)
center_lat, center_lon = nodes.geometry.y.mean(), nodes.geometry.x.mean()
m = folium.Map(location=[center_lat, center_lon], zoom_start=14)
# edge(道路)の描画
for _, edge in edges.iterrows():
# 道路のジオメトリ(線)
if "geometry" in edge:
coords = [(lat, lon) for lon, lat in edge["geometry"].coords]
folium.PolyLine(coords, color="blue", weight=2.5, opacity=0.7).add_to(m)
# node(交差点)の描画
for _, node in nodes.iterrows():
folium.CircleMarker(
location=(node.geometry.y, node.geometry.x),
radius=3, # マーカーのサイズ
color="red", # 枠の色
fill=True,
fill_color="red", # 塗りつぶしの色
fill_opacity=0.7,
).add_to(m)
# 地図を保存
m.save("road_network.html")
今回の記事では、計算量上の理由から以下の地図に示す庭園北側のみを対象とします。計算量の話については実装の方で詳しく説明しますが、ナイーブな実装で計算できる限界の範囲を対象としました。
実装
計算量の話をするために、以降ではNode(頂点)の数を$N$、Edge(辺)の数を$M$で表します。処理によって着目するグラフが異なるので、具体的な値などは処理ごとに記載しますが、特に地図の特性上、$M \sim 4N$程度で抑えられることを覚えておきましょう。これは、1つ交差点に対して平均4本程度の道がつながっていると考えると、道路の数は交差点の数の高々4倍となるためです3。
前処理
前処理の工程として、データフレームではなくグラフの形式でデータを保持しておく方が都合がよいので、競技プログラミングでもおなじみの形に変換しておきます。地図データのNodeのIDとグラフの頂点番号を相互に変換できるリストと、各頂点から行くことができる頂点と距離のリストを作成します。
node2idx = dict() # node番号からインデックスを参照する
idx2node = [0] * len(nodes) # インデックスからnode番号を参照する
for i, x in enumerate(nodes.iterrows()):
node2idx[x[0]] = i
idx2node[i] = x[0]
# 各頂点について、(行き先, 距離)のリストを作成
all_to = [[] for i in range(len(nodes))]
for x, edge in edges.iterrows():
u, v, key = x
# edgesには有向グラフとして道路の情報が格納されているので、逆向きは登録しなくてもよい
all_to[node2idx[u]].append((node2idx[v], edge.length))
to = [x[:] for x in all_to] # 道路全体のグラフをコピーしておく
もう一つの前処理として、地図に含まれる行き止まりを処理します。行き止まりは端まで行ったら必ず引き返さないといけないため、考えるまでもなく手順が決まっています。そこで、行き止まりは一筆書き構築時以外では除外し、計算量を削減します。この処理をすることで結果として、全ての頂点の次数が2以上になります。
一つ目の処理は$O(N+M)$、二つ目の処理は$O(NM)$で計算できます。
q = [] # 辺の数が1の頂点のリスト
for i in range(len(nodes)):
if len(to[i]) == 1:
q.append(i)
deadends = [] # 行き止まりに繋がる辺のリスト
while q: # 行き止まりの頂点がなくなるまで繰り返す
u = q.pop()
v, _ = to[u].pop() # v:行き止まりと反対側の頂点
deadends.append((u, v))
idx = 0
for i in range(len(to[v])):
if to[v][i][0] == u:
idx = i
_ = to[v].pop(idx) # 頂点vから行き止まりへ行く辺の削除
if len(to[v]) == 1: # 頂点vの次数が1 = 頂点vが行き止まり
q.append(v)
1. 地図上で繋がっている道路が奇数の交差点同士の距離を求める
任意の2点間同士の最短距離を計算するアルゴリズムとして、ワーシャルフロイド法(Wikipedia)があります。全頂点に対して2点間の最短距離を求めて、奇数頂点の情報だけを取り出すという実装にします。計算量は$O(N^3)$です。この地図では、奇数頂点は6つでした。
# 奇数次元の頂点
even_nodes = []
N = len(nodes)
for i in range(N):
if len(to[i]) % 2 == 1:
even_nodes.append(i)
# 距離行列を作成(ワーシャルフロイド法)
dist = np.zeros((N, N))
INF = 10 ** 9
dist[:, :] = INF
for i in range(N):
dist[i, i] = 0
for x, d in to[i]:
dist[i, x] = d
for k in range(N):
for i in range(N):
for j in range(N):
dist[i, j] = min(dist[i, j], dist[i, k] + dist[k, j])
even_dists = dist[np.ix_(even_nodes, even_nodes)] # 奇数頂点間の距離行列
2. ペア間の距離が最も小さくなるようなペアの組み合わせを求める
ある集合について、その要素同士でペアを作っていくという種類の問題を一般的にマッチング問題と呼びます。その中でも、ペア間の距離やコストなどの総和が最小になるようにペアを構成する問題を最小マッチングと呼びます。また、男女でペアを組むといったような、2つの集合からペアを作るタイプの問題を二部マッチングと呼びます。今回のペアを作る問題は、特に二部グラフの形になっているというわけではないので、「一般最小マッチング問題」と呼ばれる問題になると思います。
この問題の解法はいくつか存在しますが、この記事では最も単純な「総当たり解法」で実装します。やりたいことは、全てのペアの組み合わせについて距離の総和を計算して、その中でもっとも和が小さいものを採用するということです。
実装は、奇数頂点の番号が並んだ数列の全ての並べ替えについて、先頭から順に2つずつをペアとして2点間の距離を足しこんでいくと、全ての組み合わせを試すことができます4。この実装だと計算量は$O(N!)$となり、全体の計算の中でもっとも計算が重い部分です。
from itertools import permutations
min_dist = float("INF") # 合計距離の最小値
min_pair = [] # 合計距離が最小になる順列
N = len(even_dists)
for x in permutations(range(N)):
sum_distance = 0 # 合計距離
for i in range(N//2):
sum_distance += even_dists[x[2*i], x[2*i+1]]
if min_dist > sum_distance:
min_pair = x
min_dist = sum_distance
# 最適マッチングの結果を格納
pairs = []
for i in range(N//2):
pairs.append([even_nodes[min_pair[2*i]], even_nodes[min_pair[2*i+1]]])
pairs
3. ペア間の道路を二重にして、一筆書きの手順を構築する
先ほど求めたペア間の最短経路はダイクストラ法で計算することができます。計算量は1ペアにつき最大で$O((N+M)\log N)$ですが、ペア間の頂点数は非常に少ないので、ほぼ$O(M)$とみなしてもよいくらいのオーダーで計算できると思います5。
ペア間の道路と、1.で無視していた行き止まりに行くための道路を二重にすることで、全ての頂点の次数が偶数のグラフを作ることができます。この時点でグラフに組み込まれている道の長さを合計すると、「全ての道を1回以上通る時の最短距離」に対する答えが出ます。
# 二重化したグラフの作成
double_to = [x[:] for x in to]
for u, v in pairs:
# ダイクストラ法でペア間の最短ルートを探索
route = dijkstra(to, u, v) #ダイクストラ法の中身は省略
for i in range(len(route)-1):
x = route[i]
y = route[i+1]
for z, a in to[x]:
if z == y:
dist = a
break
double_to[x].append((y, dist))
double_to[y].append((x, dist))
# 行き止まりの道も追加する
for x, y in deadends:
for z, a in all_to[x]:
if z == y:
dist = a
break
# 2本分の辺を追加する
for i in range(2):
double_to[x].append((y, dist))
double_to[y].append((x, dist))
一筆書きの手順の構成には、Fleuryのアルゴリズムを使います。このアルゴリズムは、一筆書きができることが保証されているグラフにおいて、その手順のうちの1つを作ることができるアルゴリズムです。アルゴリズムの考え方としては、通った辺を消しながらグラフを進んでいき、今いる頂点に分岐がある場合は、残っている辺が分断されないような辺を選びながら進むというものです6。
このアルゴリズムは、「残っている辺が分断されるか否か」を判定する処理がボトルネックとなっており、判定方法としては単純なBFSやDFS、UnionFind、LowLinkなどが使えると思います。今回はUnionFindを使って実装していて、それぞれの辺について、その辺を消したときにその両端の点とスタート地点が分離しないかを確認しています。計算量は大きく見積もると$O(MN^2(M+N) + MN\alpha(N))$となりますが、1つの頂点について分岐の数はほぼ定数になる(地図が大きくなってもほぼ変わらない)ので、実際には$O(M^2)$程度で収まると思います。
start = 0 # スタートのノードの番号(= ゴールのノード)。一筆書きの終了判定に使用
now = 0 # 現在いるノードの番号
to = [x[:] for x in double_to] # 読みやすさのために名前を変えてコピー
N = len(to)
route = [start] # 頂点の訪問順序
while len(to[now]):
# 行き先が一方向しか残っていないとき
if len(to[now]) == 1:
next = to[now][0][0]
route.append(next)
_ = to[now].pop(0)
for i in range(len(to[next])):
if to[next][i][0] == now:
idx = i
break
_ = to[next].pop(idx)
now = next
continue
# 行き先が複数残っているとき。全ての行き先について、その点に進んでも問題ないかを判定する
for i in range(len(to[now])):
# ゴールに行く道が残り1つのとき
if len(to[start]) == 1 and to[now][i][0] == start:
continue # ゴールに行ってしまうと、残っている辺を通ることができないので判定をしない
u = UnionFind(N) # N頂点のUnionFind木、実装は省略。
for j in range(N):
for k in range(len(to[j])):
# 現在地とto[now]のi番目の行き先をつなぐ辺だけunionしない
if (now == j and i == k) or (to[now][i][0] == j and now == to[j][k][0]):
continue
u.union(j, to[j][k][0])
# ゴールの頂点と、現在地に繋がっている頂点が分断されていないかチェック
flag = True
for k, _ in to[now]:
#分断されている場合は、フラグをFalseにする
if not u.same(start, k):
flag = False
break
# フラグがTrueの時、次の行き先としてto[now]のi番目を採用する
if flag:
use = i
break
next = to[now][use][0]
# print(next, to[now][use])
route.append(next)
_ = to[now].pop(use)
for i in range(len(to[next])):
if to[next][i][0] == now:
idx = i
break
_ = to[next].pop(idx)
now = next # 次の行き先を現在地とする
結果・描画
実装で示したプログラムを順に並べて実行すると、全ての道を通ることができる最短順路を計算できます。こちら道順をわかりやすく見るために、動的な地図をfoliumで作成しました。
総移動距離は1229mで、徒歩5km/hで回覧した場合は約15分かかる計算です。
まとめ
今回は、香川県高松市にある日本最大の文化財庭園「栗林公園」を最速で巡るために、公園内の一部の範囲の道をすべて通りつつ、最短で回覧する道順を構成するプログラムを作成しました。処理ごとの計算量オーダーは以下の表のとおりです。今回の計算では、奇数交差点同士のマッチング問題を解くところが計算のボトルネックとなっていて、$O(N!)$の計算量がかかるため園内の$1/6$程度の範囲での解を得ました。
| 手順 | 内容 | 計算量オーダー |
|---|---|---|
| 前処理 | データの変換 | $O(N + M)$ |
| 行き止まりの削除 | $O(NM)$ | |
| 1 | 奇数点同士の距離の計算 | $O(N^3)$ |
| 2 | マッチングの探索 | $O(N!)$ |
| 3 | ペア間の最短ルートの計算 | $O(N(N+M)\log N)$ |
| 一筆書き手順の構築 | $O(MN^2(M+N) + MN\alpha(N))$ |
狭い範囲での解ですが、これだけ範囲で15分かかることを考えると、園内全て周回するためにはかなりの時間がかかると予想されます。次の記事では、この部分の計算量を複数の方法で改善することによって園内全体での最適解を求める予定です。
-
ループするような順路を構築すれば、好きな場所をスタートとしてよいため、どの入り口から入っても同じ手順を使って全ての道を通ることができます。一見すると考えることが増えて面倒くさそうな制約に見えますが、アルゴリズムを構築する流れで自然に出てくる制約なので、この制約を入れておく方が色々と話が単純にすみます。(詳しい説明は割愛します) ↩
-
この説明では、「一筆書きができること」⇒「全ての交差点の繋がっている道路の本数が偶数本」を証明できますが、実は逆向きの矢印(十分性)の証明はできません。これ以降の説明でも十分性が成り立つことを前提にしていますが、証明についてはグラフ理論の話に踏み込んでしまうため割愛します。 ↩
-
実際には、1つの道路に対して2回カウントして数えている計算なので、道路の数$M$はさらに半分で抑えることができます。 ↩
-
順列による総当たりは同じペア構成を何度も計算するため、さらに非効率です。実際のペアの作り方の総数はペアの数を$P = N/2$として、$(2P)!/2^PP!$で表されるので、分母の分だけ重複して計算しています。再帰などを駆使して、同じ組み合わせを何度も計算しないようにすることで、同じ総当たりでもより効率よく計算できます(多分)。適切に列挙できる場合なら、$N=12$くらいまでは計算できるようになると思います。 ↩
-
1のワーシャルフロイド法で経由地や最短経路を適切に前計算しておいて、その情報を経路計算に使うことで、全ペア分の経路を$O(M)$で計算することも可能です。 ↩
-
$O(M)$で計算できるHierholzerのアルゴリズムというのもあるそうです。今回は$O(M^2)$でもボトルネックにはならないので、考え方が少しだけわかりやすいFleuryのアルゴリズムを採用しました。 ↩