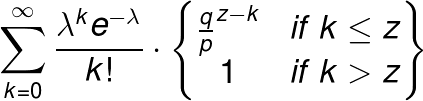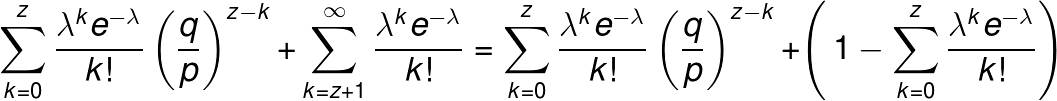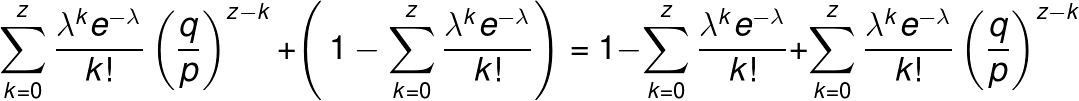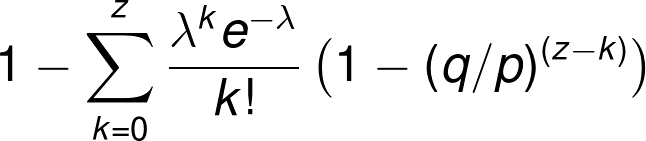公開されているブロックチェーンはパブリックチェーンと呼ばれています。このタイプのブロックチェーンでは、正しいデータを一意に決定するプロセスとして「Proof of Work」が採用されているものが多いです。そしてこの仕組みには、ファイナリティ(決済完了性)がないという性質があります。これは端的にいえば、資産を誰かに送ってもそれが確かに着金したと認めることができないという性質です。「え、それでお金として使えるの?」という疑問が出てきそうですが、その解決策として「確率的ファイナリティ」という概念が導入されています。今回は、確率的ファイナリティについて実際に計算をしつつ、深く掘り下げていきます。
ファイナリティ(決済完了性)とは
ファイナリティとは「決済が確定したとみなせること」を指します。普段使っているお金であれば、100円玉をレジの店員に手渡すとその時点で100円玉の所有権が移るため、そこで決済が確定したとみなすことができます。銀行振込の場合でも、口座を管理している銀行がその送金を認めさえすれば、その決済は完了します。
しかし、パブリックチェーンではそのファイナリティが確率的に確定します。言い換えるならば、このくらい時間がたったら(マイニングが進んだら)決済が確定したと認めても問題ないでしょう、ということです。そのため、マイニングが成功すれば安泰というわけではなく常にそれが覆る可能性を持っていることになります。
ハッシュパワー≒計算能力
確率的なファイナリティを考える前に「ハッシュパワー」の概念を押さえておきましょう。ハッシュパワーは、計算能力のような意味で、マイニングに参加しているマシンの計算能力を表しています。当然、計算能力が高くなればなるほど、たくさんの計算ができるためマイニングにいち早く成功します。
また、ハッシュパワーが異なる2つのマシンで同時にマイニングを開始した場合には、ハッシュパワーがより大きなマシンの方がいち早くマイニングに成功し競争に勝つことができます。
サトシナカモトの考え方
ビットコインの核となるアイデアをまとめた原典とも言われる論文『Bitcoin: A Peer-to-Peer Electronic Cash System』でも、確率的なファイナリティについて間接的に触れています。
第11章の「Calculations」という章に、Proof of Workが悪意のある攻撃にどの程度強いのかを実際に確率を計算して検証している部分があります。ここでいう攻撃とは、一度マイニングに成功したブロックがそれよりも長いチェーンによって失効させられてしまう攻撃のことをいいます。Proof of Workでは一番長いチェーンが正しい情報であるとするルールがあるため、現時点で最長だと思っていても、より長いチェーンが出てきた場合、そちらが“正義”となります。もしも頻繁にブロックが失効して取引が無効になるという現象が頻繁に起こるとすれば、ファイナリティはおろか、通貨として全く使い物にならなくなるため、この部分は重要なパートの一つです。
さて、サトシナカモトの論文では、統計学のポワソン分布を用いて以下のように計算しています。(数式アレルギーの方は、次の章まで飛ばしてください……)
なお、各変数の意味は以下の通りです。
| 変数・定数 | 意味 |
|---|---|
| p | 善意のマイナーがマイニングに成功する確率 |
| q | 悪意のマイナーがマイニングに成功する確率 |
| z | あるトランザクションがブロックに格納されてからその後ろに繋がっているブロックの数 |
| λ |  |
| e | ネイピア数(自然対数の底) |
ちなみに、マイニングは善意のマイナーと悪意のマイナーのどちらかが必ず成功するので、$p+q=1となります。場合分けも入って複雑ですが、大まかには以下の通りです。まず、zブロックだけ遅れている攻撃者がマイニングを成功させて正しいブロックチェーンに追いつく確率は*$ (q/p)^z $*です。$ (q/p) $はブロックを一つだけマイニングできる確率で、q=0.1なら1/9となります。それがz回(zブロック分)続くので、z回かけてz乗します。
*$ \frac{λ^ke^{-λ}}{k!} $*の部分は、ポワソン分布の確率密度関数というもので、どのくらいの確率で発生するのかを計算するものです。ちなみに、ポワソン分布はランダムに発生する事象を扱う際に利用されることが多く、品質管理や事故率の計算の際に利用されることが多いです。
以上の二つの事象がともに起こる確率は、*$ \frac{λ^ke^{-λ}}{k!} (\frac{q}{p})^z $*と掛け算してやれば算出できます。
そして上記の式を、zの値がkより大きい場合と小さい場合でシグマを分けてあげます。その後、右辺のように全確率(1)から事象が起こらない確率を引くことで表現します。このような考え方を余事象といいます。こうすることで、なんと無限大が消えて、0からzまでのシグマを考えればよくなります。
その後上の式の右辺を、下の式の右辺のように整理してあげれば……
下の式が出来上がります。この式はサトシナカモトの論文でも登場しますが、無限大がなくなった上に、シグマが一つだけなのでプログラムでも扱いやすくなりました。
また、この論文では、この数式をコード(C言語)に落とし込んで計算しています。
# include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}
Pythonで計算してみた
論文のままC言語で計算するのもありなのですが、(個人的に)科学計算関係はPythonの方が得意なので、Pythonに変換しちゃって計算しましょう。
攻撃者が成功する確率
Pythonにすると以下のようになります。
import numpy as np
def attcker_success(q, z):
p = 1.0 - q
l = z * (q/p)
sum = 1.0
for k in range(0, z+1):
poisson = np.exp(-l)
for i in range(1, k+1):
poisson *= l / i
sum -= poisson * (1 - np.power(q/p, z-k))
return sum
変数の使い方や計算の手順などはほぼそのまま利用しています。以下のコードを実行すれば、q=0.1、z=10の確率、つまり悪意のあるマイナーが10%の確率で成功マイニングに成功し、善意のマイナーより10ブロックも長くブロックをつなげられた場合の確率が計算できます。
print('{:.50f}'.format(attcker_success(0.1, 10)))
0.00000124140217479795642434325410319306826067986549
もう少し、いろいろなパターンで確率を計算してみましょう! for文で、zの値が0から10の場合の確率を計算して出力してみます。
for z_i in range(0,11):
print("z=",z_i,' {:.50f}'.format(attcker_success(0.1, z_i)),sep='')
z=0 1.00000000000000000000000000000000000000000000000000
z=1 0.20458727394278242162073411236633546650409698486328
z=2 0.05097789283933862325426389361382462084293365478516
z=3 0.01317224167889648189788687204782036133110523223877
z=4 0.00345524346648517360902630457530904095619916915894
z=5 0.00091368218792791224339144839916571072535589337349
z=6 0.00024280274536281863662079416599226533435285091400
z=7 0.00006473531692709972641154581030065173763432539999
z=8 0.00001729980418716505960723822665769944251223932952
z=9 0.00000463116397250268184871292015403199116008181591
z=10 0.00000124140217479795642434325410319306826067986549
サトシナカモトの論文にある確率と比較してみると一致していることがわかりますね。

※N.Satoshi(2008)より抜粋
グラフにしてみた
ここまでは確率を計算してみましたが、グラフに描写して可視化してみましょう。ここまでのコードを引継ぎつつ、以下のようにコードを書いてみます。
import numpy as np
import matplotlib.pyplot as plt
def attcker_success(q, z):
p = 1.0 - q
l = z * (q/p)
sum = 1.0
for k in range(0, z+1):
poisson = np.exp(-l)
for i in range(1, k+1):
poisson *= l / i
sum -= poisson * (1 - np.power(q/p, z-k))
return sum
def attcker_plot(q, z):
probability = []
progress = []
for z_prg in range(z+1):
progress.append(z_prg)
probability.append(attcker_success(q, z_prg))
plt.plot(progress, probability)
plt.show()
先ほど確率を計算したq=0.1、z=10の場合のグラフを描写してみましょう。以下のように引数に指定してあげれば大丈夫です。
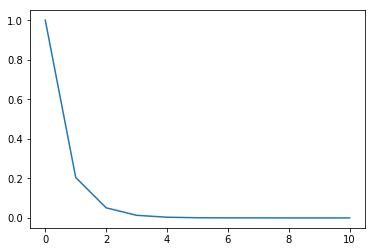
attcker_plot(0.1, 10)
出力されるグラフは以下の通りです。横軸がz、縦軸が悪意あるマイナーの成功確率です。zの値が大きくなればなるほど確率が0に近づき、4を超えたあたりから限りなく0に近くなっていることがわかりますね。
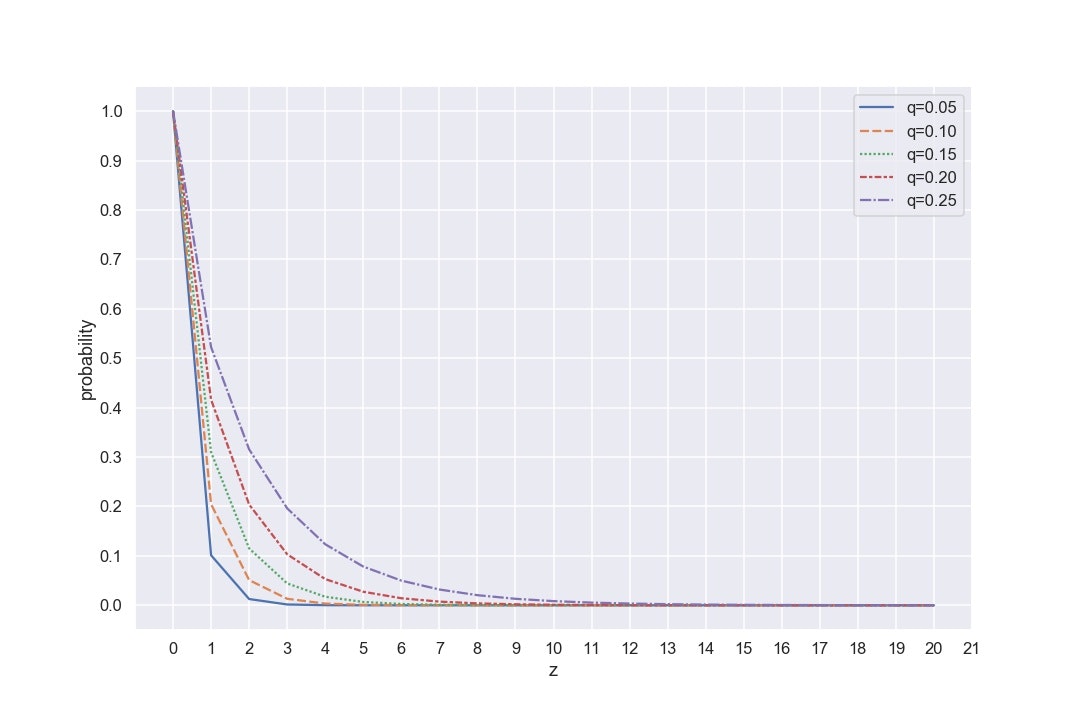
ここからはもう少しいろいろなパターンでグラフを描写してみましょう。以下のようにコードを書き換えて、qの値が0.1から0.25までの0.05刻みとして計5パターンを考えてみましょう。また、zの値は、20までに増やしています。なお、グラフは重ねて描写しています。先ほどのグラフがとてもシンプルだったので、今度はseabornを使って、少しだけ“ゴージャス”にしてみます。
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
def attcker_success(q, z):
p = 1.0 - q
l = z * (q/p)
sum = 1.0
for k in range(0, z+1):
poisson = np.exp(-l)
for i in range(1, k+1):
poisson *= l / i
sum -= poisson * (1 - np.power(q/p, z-k))
return sum
def attcker_data(q, z):
probability = []
for z_prg in range(z+1):
probability.append(attcker_success(q, z_prg))
return probability
probability_list = []
q_value_list = np.arange(0.05, 0.3, 0.05)
for q_value in q_value_list:
probability_list.append(attcker_data(q_value, 20))
df = pd.DataFrame(probability_list, index=["q=0.05","q=0.10","q=0.15","q=0.20","q=0.25"])
df = df.T
sns.set(style="darkgrid")
sns.set_context("talk")
plt.figure(figsize=(15, 10))
plt.xlabel('z')
plt.ylabel('probability')
plt.xticks( np.arange(0, 22, 1) )
plt.yticks( np.arange(0, 1.1, 0.1) )
sns.lineplot(data=df)
qの値(攻撃者の成功確率)が高くなればなるほど、グラフの変化が緩やかになっていることが分かると思います。このように攻撃者のハッシュパワーが高くなり、マイニングの成功確率が高くなればなるほど連続してブロックをつなげて独自のチェーンを作っていけることが可能です。
詰まるところ、どのくらい待てば大丈夫なのか?
さて、ここまで確率的に悪意のあるマイナーがどのくらい成功するのかを考えてきました。ファイナリティを考える際に重要な点は、一度行った取引がひっくり返されることがないという確信です。ここまでの議論を振り返ってみた時に、悪意のあるマイナーによってブロックチェーンがひっくり返されることがどの程度ありそうなのかという点で考えなくてはいけません。その意味で、確率的にファイナリティを決めてしまう必要があるわけですが、グラフをみても分かる通り、zが大きくなればなるほど、指数関数的にひっくり返す確率は小さくなっています。そのため、qの値(攻撃者の成功率)がある程度高くても、zが一定以上になれば確率は限りなく0に近づくことがわかります。
限りなく0に近づくのであれば、もはや取引を確定して決済が完了したとみなしてしまうのが現実的といっていいのではないか、それこそが確率的ファイナリティの根拠になっています。
実際にビットコインの場合、トランザクションは6ブロック経過して初めて決済が完了したとみなされます。ビットコインの場合は一つのブロックが平均10分でマイニングされるため、決済完了までにおおよそ1時間待つ必要があることになります。先ほどのグラフをみてみると、6ブロックつながった場合にそのチェーンをひっくり返してしまう可能性は、0に近い確率となっています。(0ではありませんが。。。)
また、マイナーがマイニングに成功した際にマイニング報酬を受け取ることができますが、これはそのマイナーがマイニングしたブロックから100ブロックつながらなければ利用することができないことになっています。
まとめ
今回は、確率的ファイナリティを統計学的に確認してみました。パブリックチェーンではどこの誰が何人ネットワークに参加しているのか分からないので、マシンの計算能力を使うことで不正を防ごうとしています。ここで紹介した通り、確率的に考えてみれば、管理者のいないシステムにおいても正しさを担保できるようですね。
ただし、ある程度条件が揃ってしまうと、攻撃が成功して取引がなかったことにされたり、存在しない取引をあったことにされたりといった不正ができるようになってしまいます。このことについては別の記事で紹介します。
参考文献
N.Satoshi(2008)"Bitcoin: A Peer-to-Peer Electronic Cash System"