0. はじめに
非負整数 $n$ に対して $1...n$ の全ての整数の積を $n$ の階乗(factorial)と呼び、$n!$ で表します。ただし、$0! = 1$ と定めます。
例えば、
4! = 1 \times 2 \times 3 \times 4 = 24
です。
これを Python で計算する場合、
def factorial_naive(n: int) -> int:
result = 1
for i in range(1, n + 1):
result *= i
return result
print(factorial_naive(4)) # 24
のように書くことができます。また、再帰関数の紹介でよく例示されているように、以下のようにしても計算できます。
def factorial_recursive(n: int) -> int:
if n == 0: return 1
return n * factorial_recursive(n - 1)
print(factorial_recursive(4)) # 24
このように、階乗を計算するコードは簡単に書けますが、mathモジュールにはfactorial()という関数があるので、これを使うことでより簡単に階乗を計算できます。
import math
print(math.factorial(4)) # 24
これらの方法のうちどれを使ってもいいですが、math.factorial()はfactorial_naive() や factorial_recursive()に比べて高速に計算でき、特に、$n$ が大きい場合には体感できるほどの差が生まれます。
実際に、factorial_naive(50000) と math.factorial(50000)をそれぞれ実行してみるとその差が体感できると思います。
math.factorial()はC言語で実装されており、一方factorial_naive()はPythonで記述したのでmath.factorial()の方が速いのは当然だと思うかもしれません。しかし、実はそれだけでなく、math.factorial()のアルゴリズムはいくつかの工夫によって、ナイーブに計算するよりも高速に計算できるようになっています。
本記事では math.factorial()がどのように階乗を計算しているのかを見ていきます。
なお、本記事で参考にしたソースコードは以下で見ることができます。
https://github.com/python/cpython/blob/3.11/Modules/mathmodule.c
1. 工夫1: ビットシフトに置き換える
整数に $2$ を掛ける操作は左ビットシフト<< 1 に置き換えることができます。こちらの方がコストが小さいので、出来る限りビットシフトに置き換えます。
例えば、$7!$ は
\begin{aligned}
7! &= 1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \\
&= 1 \times 2 \times 3 \times 2^2 \times 5 \times (2 \times 3) \times 7 \\
&= 1 \times 3 \times 5 \times 3 \times 7 \times 2^4
\end{aligned}
なのでまず $1 \times 3 \times 5 \times 3 \times 7 = 315$ を計算して最後にビットシフト<< 4をすればよいことがわかります。
これによって $6$ 回の掛け算を $4$ 回の掛け算と $1$ 回のビットシフト演算にすることができました。
一般に
n! = (奇数) \times (2の冪乗)
の形に表すことができ、$n$ が大きいほど演算の回数を削減できます。
以後、 $n!$ を上の式のように表した時の奇数部分を $odd\_part(n)$、$2$ の冪乗の指数部分を $two\_exponent(n)$ と呼ぶことにします。
例えば、$n = 6$ のとき
6! = (1 \times 3 \times 5 \times 3) \times 2^4
なので
\begin{aligned}
odd\_part(6) &= 1 \times 3 \times 5 \times 3 = 45\\
two\_exponent(6) &= 4
\end{aligned}
となり、45 << 4を計算すれば良いことがわかります。
ここからは、 $odd\_part(n)$、$two\_exponent(n)$ を具体的に数式で表すことを考えます。
2. odd_partを数式で表す
具体例として $n = 20$ の場合を考えることにします。
整数 $1\dots20$ を含まれる $2$ の数で分類してみると以下のようになります。
| $2$ の数 | 整数 | $2$ を除いた数 |
|---|---|---|
| $0$ | $1, 3, 5, 7, 9, 11, 13, 15, 17, 19$ | $1, 3, 5, 7, 9, 11, 13, 15, 17, 19$ |
| $1$ | $2, 6, 10, 14, 18$ | $1, 3, 5, 7, 9$ |
| $2$ | $4, 12, 20$ | $1, 3, 5$ |
| $3$ | $8$ | $1$ |
| $4$ | $16$ | $1$ |
こうしてみると
\begin{aligned}
odd\_part(20) &=(1\times3\times5\times7\times9\times11\times13\times15\times17\times19)\\
&\times(1\times3\times5\times7\times9)\\
&\times(1\times3\times5)\\
&\times(1)\\
&\times(1)\\
\end{aligned}
であることがわかります。
ここで 正の奇数 $L, U$ に対して $F(L, U)$ を
F(L, U) = \left\{
\begin{aligned}
&[L, U) の奇数の総積 \;\;\;&(L \lt U)\\
&1 & (L \geq U)\\
\end{aligned}
\right. \\
と定めると
\begin{aligned}
odd\_part(20) &= F(1, 21) \times F(1, 11) \times F(1, 7) \times F(1, 3) \times F(1, 3)\\
&= \prod_{i=0}^{4}{F\left(1, \left(\left\lfloor\frac{20}{2^i} \right\rfloor + 1\right) OR\; 1\right)}
\end{aligned}
と書けます。ただし $x\; OR\; y$ は整数 $x, y$ に対するビットごとの $or$ 演算を表します。
一般に正整数 $n$ については
odd\_part(n) = \prod_{i = 0}^{m}{F\left(1, \left(\left\lfloor\frac{n}{2^i} \right\rfloor + 1\right) OR\; 1\right)}
となります。ここで、$m$ は $\left\lfloor\frac{n}{2^m}\right\rfloor \gt 0$ となる最大の整数です。
さらに、$F(1, U) = F(3, U)$ であること、$F\left(1, \left(\left\lfloor\frac{n}{2^m} \right\rfloor + 1\right) OR\; 1\right) = 1$ であることを考慮すると
odd\_part(n) = \prod_{i = 0}^{m - 1}{F(L_i, U_i)}
ただし、
\begin{aligned}
L_i &= 3\\
U_i &= \left(\left\lfloor\frac{n}{2^i} \right\rfloor + 1\right) OR\; 1
\end{aligned}
と書けます。
3. 工夫2: 計算済みの結果を再利用する
これで $odd\_part(n)$ を数式で表すことが出来ましたが、このまま計算してはナイーブな方法と変わりません。
そこで計算の順序を工夫することで効率化します。
正の奇数 $a \leq b \leq c$ に対して
F(a, c) = F(a, b) \times F(b, c)
であることを使うと $odd\_part(20)$ は
\begin{aligned}
odd\_part(20) =& F(3, 21) \times F(3, 11) \times F(3, 7) \times F(3, 3)\\
=& F(3, 3) \times F(3, 7) \times F(7, 11) \times F(11, 21) \times\\
& F(3, 3) \times F(3, 7) \times F(7, 11) \times\\
& F(3, 3) \times F(3, 7) \times\\
& F(3, 3)\\
\end{aligned}
となります。このようにみると共通している部分が多くあることがわかります。したがって、共通部分の計算を省略することで効率的に計算できます。
具体的には、$i = m - 1, m - 2, \dots ,0$ の順に計算し、$i = j$ での計算では $F(U_{j + 1}, U_j)$ のみ計算し $i = j + 1$ の結果に掛ければ良いことになります。
4. 工夫3: 多倍長演算を回避する
$F(L, U)$ の計算は掛け算なので非常に大きくなり得ます。そこで、掛け算の順番を工夫することで、重い多倍長演算をできるだけ回避します。
具体例として $F(11, 99)$ の計算を考えます。
$F(11, 99)$ は $64$ ビット整数を超えるので区間 $[11, 99)$ を半分に分割し、$F(11, 55) \times F(55, 99)$ とします。このような分割を $F(L, U)$ が $64$ ビット整数に収まるまで繰り返すと
\begin{aligned}
F(11, 99) =& F(11, 33) \times F(33, 45) \times F(45, 55) \times F(55, 67) \times\\
&F(67, 77) \times F(77, 89) \times F(89, 99)
\end{aligned}
となります。
このように計算することで $F(11, 99)$ の計算における $43$ 回の掛け算のうち、多倍長演算は $\boldsymbol{6}$ 回で済みます。
$11$ から順に掛けていく方法では $39$ を掛けた時点で $64$ ビット整数を超えるため、$\boldsymbol{30}$ 回の多倍長演算を行うことになります。
これで $odd\_part(n)$ の計算アルゴリズムがわかりました。
5. two_exponent を数式で表す
$two\_exponent(n)$ は $n!$ に含まれる $2$ の数なので、これは ${1, 2, \dots , n}$ のうちの $(2 の倍数の数) + (4 の倍数の数) + \cdots$ に等しいです。
したがって、
two\_exponent(n) = \sum_{i=1}^{m}{\left\lfloor\frac{n}{2^i} \right\rfloor}
です。$m$ は $\left\lfloor\frac{n}{2^m}\right\rfloor \gt 0$ となる最大の整数なので $\log{n}$ 程度であり、この式を用いれば十分高速に $two\_exponent(n)$ を計算できます。
しかし、実はより簡潔に表すことが出来、
two\_exponent(n) = n - popcount(n)
です。ただし $popcount(n)$ は $n$ を $2$ 進数表記したときの'1'ビットの数です。
$\boldsymbol{\sum_{i=1}^{m}{\left\lfloor\frac{n}{2^i} \right\rfloor} = n - popcount(n) の証明}$
$n = 0$ のときは明らかです。
$n$ を $1$ 以上の整数とし、$m$ を $\left\lfloor\frac{n}{2^m}\right\rfloor \gt 0$ となる最大の整数とします。このとき、$0, 1$ からなる長さ $m + 1$ の適当な整数列 $a = \{a_0, a_1, \cdots a_{m}\}$ を用いて
n = \sum_{i=0}^{m}{a_{i} 2^{i}}
と表すことが出来ます。($2$ 進数で表記することと同じです。)
これを使うと
\begin{aligned}
\sum_{i=1}^{m}{\left\lfloor\frac{n}{2^i} \right\rfloor} =& \sum_{i=1}^{m}{\left\lfloor\frac{ \sum_{j=0}^{m}{a_{j} 2^{j}}}{2^i} \right\rfloor}\\[3ex]
=& \sum_{i=1}^{m}{\left\lfloor\frac{ a_{0} 2^{0} + a_{1} 2^{1} + \cdots + a_{m} 2^{m}}{2^i} \right\rfloor}\\[1ex]\\
=& \sum_{i=1}^{m}\left\{{\left\lfloor\frac{ a_{0} 2^{0} + a_{1} 2^{1} + \cdots + a_{i - 1} 2^{i - 1}}{2^i} \right\rfloor} + \sum_{j = i}^{m}{a_{j}2^{j - i}}\right\}\\[3ex]
=& \sum_{i=1}^{m}{\sum_{j = i}^{m}{a_{j}2^{j - i}}}
\end{aligned}
となります。最後の行へは $2^0 + 2^1 + \cdots + 2^{i-1} \lt 2^i$ を使っています。
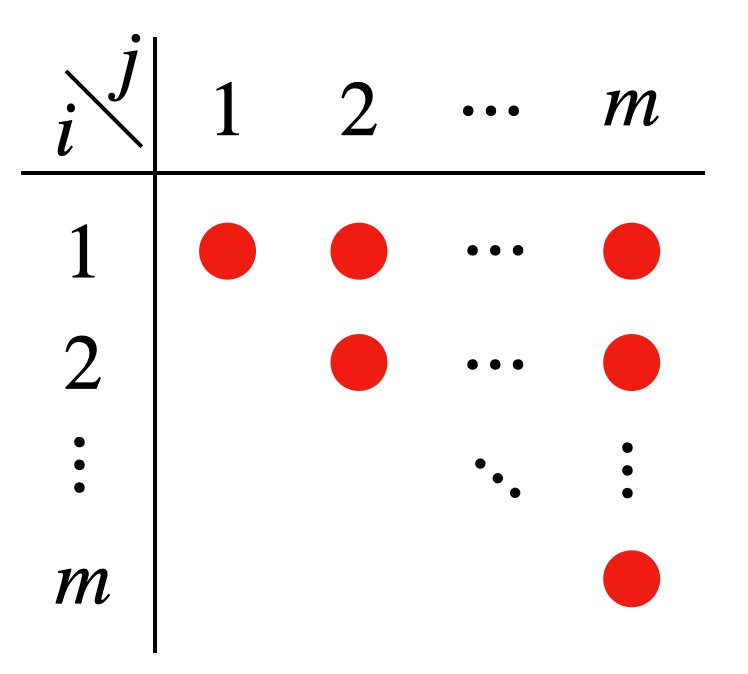
ここで、$i, j$ の和をとる範囲を考えてみると下図の赤点のようになっています。
したがって、
\begin{aligned}
\sum_{i=1}^{m}{\sum_{j = i}^{m}{a_{j}2^{j - i}}} =& \sum_{j=1}^{m}{\sum_{i = 1}^{j}{a_{j}2^{j - i}}}\\[1ex]
=& \sum_{j=1}^{m}{a_{j}2^{j} \sum_{i = 1}^{j}{2^{-i}}}
\end{aligned}
と書き換えることが出来ます。
$i$ についての和は等比数列の和なので
\begin{aligned}
\sum_{i = 1}^{j}{2^{-i}} =& \frac{\frac{1}{2}\left\{\left(\frac{1}{2}\right)^{j} - 1\right\}}{\frac{1}{2} - 1}\\[2ex]
=& 1 - 2^{-j}
\end{aligned}
です。よって
\begin{aligned}
\sum_{i=1}^{m}{\left\lfloor\frac{n}{2^i} \right\rfloor} =& \sum_{j=1}^{m}{a_{j}2^{j} (1 - 2^{-j})}
\end{aligned}
となります。また、$j = 0$ のとき
a_{0}2^{0}(1 - 2^{-0}) = a_{0}\cdot1\cdot(1 - 1) = 0
なのでこれを加えることができ、
\begin{aligned}
\sum_{i=1}^{m}{\left\lfloor\frac{n}{2^i} \right\rfloor} =& \sum_{j=0}^{m}{a_{j}2^{j} (1 - 2^{-j})}\\
=& \sum_{j=0}^{m}{a_{j}2^{j}} - \sum_{j=0}^{m}{a_{j}}
\end{aligned}
が得られます。
第 $1$ 項は $n$ そのものであり、第 $2$ 項は $n$ を $2$ 進数表記した時の'1'の数なのでこれは $popcount(n)$ です。
以上より
\sum_{i=1}^{m}{\left\lfloor\frac{n}{2^i} \right\rfloor} = n - popcount(n)
がいえました。
6. 工夫4: 結果の埋め込み
ここまで見てきたようにmath.factorial()のアルゴリズムは少々複雑です。そのため、$n$ が小さい場合にはナイーブに計算するよりも遅くなってしまいます。また、$n$ が小さい場合の方が使われる機会も多いと思います。
これらの対策として、$n$ が小さい場合は
SmallFactorials = [1, 1, 2, 6, 24, 120]
のように結果がソースコードに埋め込まれています。これによって例えば math.factorial(4)が呼ばれた場合には
return SmallFactorials[4]
とするだけで良くなります。
math.factorial()の実装では階乗の結果が64ビット整数に収まる $n \le 20$ について埋め込まれています。1
7. まとめ
$n!$ を計算するmath.factorial(n)のアルゴリズムのポイントをまとめると以下のようになります。
- $n$ が小さいときは埋め込んだ結果を使う(工夫4)
- $n$ が大きいときは
- 奇数の掛け算とビットシフトに分ける(工夫1)
- 同じ区間の積が何度も現れるので結果を使い回す(工夫2)
- 分割統治法で多倍長演算をできるだけ回避しながら計算する(工夫3)
8. 実装
def F(L: int, U: int) -> int:
"""
L, U: 奇数
[L, U) の奇数の総積を分割統治法で計算する。
"""
if L >= U: return 1
max_bits = (U - 2).bit_length() # 掛けられる最大の奇数のビット長
num_operands = (U - L) // 2 # 掛けられる奇数の個数
# [L, U) の奇数の総積のビット長は max_bits * num_operands を超えない
# これが long に収まれば多倍長演算を回避して計算できる
if max_bits * num_operands < 63: # 63 = sys.maxsize.bit_length()
total = L
for i in range(L + 2, U, 2):
total *= i
return total
# 多倍長演算を回避するために分割して計算する
mid = (L + num_operands) | 1
left = F(L, mid)
right = F(mid, U)
return left * right
def calc_odd_part(n: int) -> int:
"""
n! を (奇数) * (2の冪乗) と表したときの (奇数) の部分を計算する
"""
result = 1
L_i = 3
tmp = 1 # F(3, U_i)
m = n.bit_length() - 1 # n // (2 ** m) > 0 となる最大の整数
for i in range(m - 1, -1, -1):
# U_i は n//(2**i) より大きい最小の奇数
U_i = ((n >> i) + 1) | 1
# [1, U_i) のうち、[1, L_i) は計算済みなので再利用し [L_i, U_i) のみ計算する
tmp *= F(L_i, U_i)
# 計算済みの範囲を更新 (L_{i} <- U_{i + 1})
L_i = U_i
result *= tmp
return result
SmallFactorials = [1, 1, 2, 6, 24, 120, 720, 5040, 40320, 362880, 3628800,
39916800, 479001600, 6227020800, 87178291200, 1307674368000,
20922789888000, 355687428096000, 6402373705728000,
121645100408832000, 2432902008176640000]
def factorial(n: int) -> int:
"""
n! を計算する
"""
# n が小さい場合は埋め込んだ結果を使う
if n <= 20: return SmallFactorials[n]
# n! = odd_part * (2 ** two_exponent) と表せる
odd_part = calc_odd_part(n)
two_exponent = n - bin(n).count('1') # n - popcount(n)
return odd_part << two_exponent
"""
test
"""
import math
for n in range(1000):
assert factorial(n) == math.factorial(n)
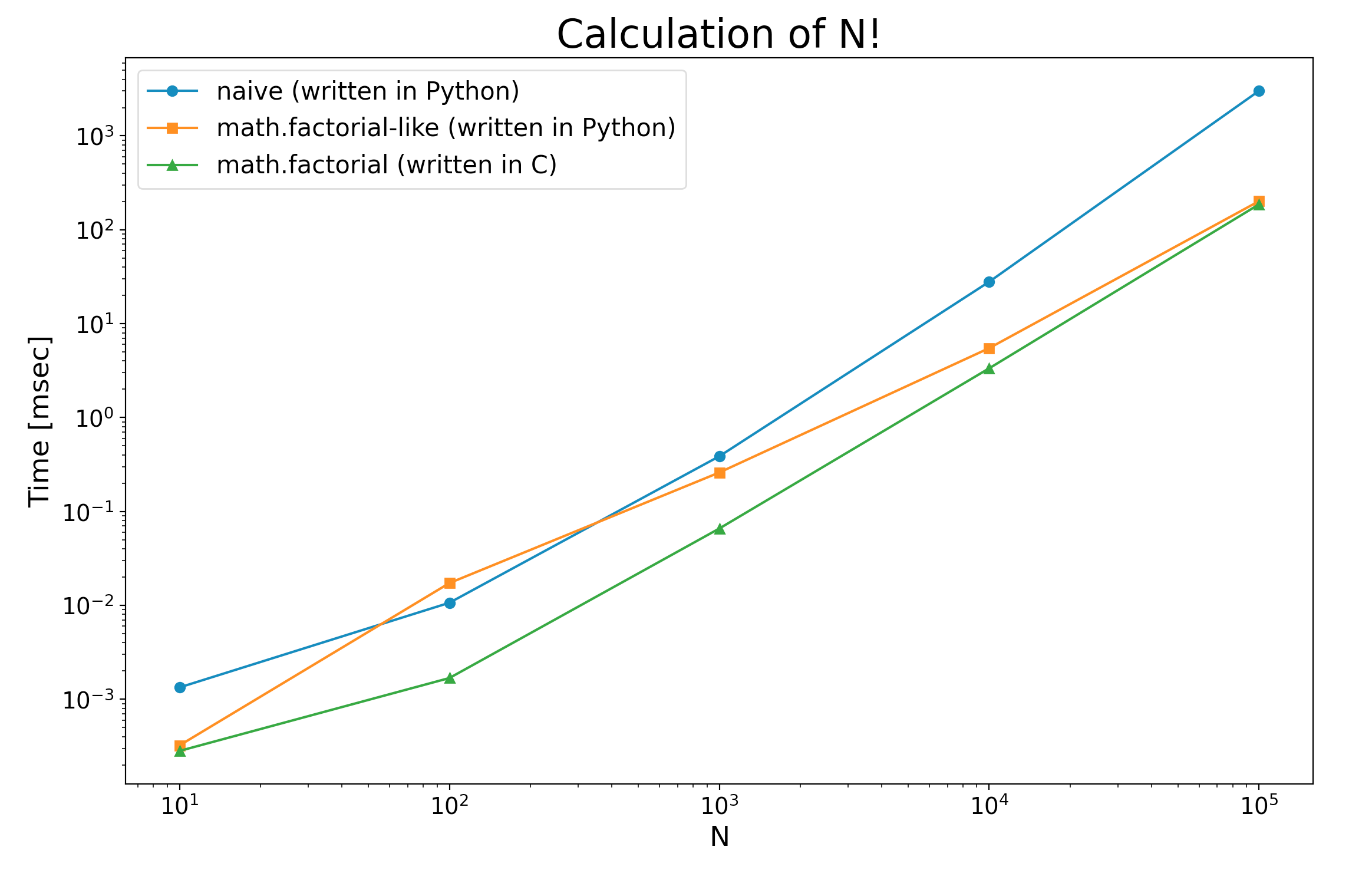
9. 速度の比較
timeitモジュールを使って
factorial_naive()factorial()math.factorial()
の速度を比較しました。使用したバージョンはPython 3.8.2 です。
$n = 10^1$ では、結果を埋め込んだfactorial()、 math.factorial()が高速です。
$n = 10^2$ では、言語(PythonかCか)が重要で、同じ Python ではアルゴリズムが単純な factorial_naive() の方が高速でした。
$n = 10^5$ までいくとアルゴリズムによる差が大きくなり、言語の差はアルゴリズムの差に比べて無視できるほど小さくなりました。
10. おわりに
Pythonのmathモジュールを使って階乗を計算する際のアルゴリズムを調べた結果、様々な工夫がされていることがわかりました。
説明の間違いやバグ、アドバイス等ありましたらお知らせください。
-
正しくは、実行環境での
unsigned long型のビット数によって変わりますが、本記事ではunsigned long型が64ビット整数を表すこととします。 ↩ -
一部説明しやすさのために
math.factorial()とは違う形にしていますが、アルゴリズムの重要なポイントは同じです。また、ここまでの説明と合わせることを重視し、Pythonで推奨される記法に準拠していない部分があります。 ↩ -
math.factorial()と合わせるためにF(L, U)の計算において、結果が $2^{63}$ におさまるように分割していますが、Python で記述する場合にはより良い分割があると思われます。 ↩