この記事は創薬 Advent Calendar 2017 (#souyakuAC2017) の21日目の記事です。今日は創薬のお話、特にStructure-based drug designにまつわるお話を書こうと思います。これまでの創薬Advent Calendarを見たところLigand-based drug design系が多かったので、ちょっとこっちの話も書こうかなと思った次第です。
最近サーバー管理のお仕事や計算に使っているスパコンの定期メンテ期間によってつれづれなるままに、日くらしパソコンにむかひて心に移りゆくよしなし事をそこはかとなく書きつくれば超長文ができあがってしまいました。ゆっくりして読んでいってね。
タンパク質とStructure-based drug designについて
タンパク質の形
タンパク質はヒトや動植物、さらには細菌やウィルスを構成する生体分子です。これらは通常20種類のアミノ酸がペプチド結合で数珠状につながっていき、それらが折りたたまって立体構造を構築しています。この立体構造は生体内での化学反応を触媒する重要な足場になります。例えば有名な例の1つとしてインフルエンザのノイラミニダーゼというタンパク質を挙げます。これはインフルエンザウィルスの型で示されるH1N1とかの、このNの部分を表しています(Hはヘマグルチニンを表しています)。このノイラミニダーゼを簡単に説明すると、インフルエンザウィルスがヒトの細胞に感染し、細胞内でウィルスを育てて、その細胞から外へ離れていく時に必須なタンパク質です(詳細はWikipediaとかを読んでね)。このノイラミニダーゼが働かないとインフルエンザウィルスは他の細胞に飛び移って増殖することができなくなり、そうして増えにくくなったインフルエンザウィルスを白血球が倒してくれれば、健康を取り戻せるわけです。
このノイラミニダーゼ阻害剤として有名なのはオセルタミビル(商品名:タミフル)とかザナミビル(商品名:リレンザ)などです。これらはノイラミニダーゼの活性部位にはまって上述の細胞増殖機能を阻害する働きを示しています。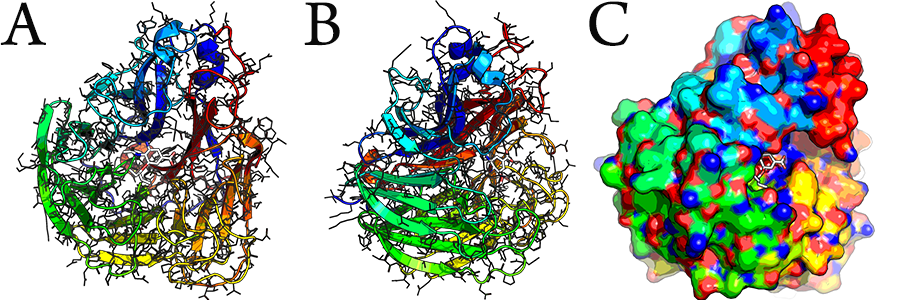
この図でカラフルなのがノイラミニダーゼ(PDB:2hu4、Group-1 H5N1 avian influenza neuraminidase)、真ん中にはまってる白い化合物がオセルタミビルです。
このNature 2006年の元論文を読んでみますと、当時はもっぱらGroup-2(N2やN9型)ノイラミニダーゼがstructure-basedの研究対象とされ、この図で示しているGroup-1のノイラミニダーゼはまだ研究対象にそれほどなっていなかったそうです。しかし、構造を解いてみるとGroup-2のくぼみの形(図Cがわかりやすい)がGroup-1のそれとは違うということが判明しました。そしてこの違いを認識してこれにはまる化合物の形を作るように心がければ、Group-1型ノイラミニダーゼを対象とした新しい阻害剤、つまり抗インフルエンザのお薬を作れるのではないか、ということでした。
Structure-based drug design(構造ベースの創薬)
こうしてタンパク質の形を認識した上で、これにはまるような形をした化合物を見つけることができれば、それが「お薬」になる可能性があるということです。しかし実際には、この見つけてきたお薬候補が人体の健康上重要なタンパク質にも結合してしまって、その働きを鈍らせる「毒」になってしまうと良くないので(これを薬の副作用という)、治験を何度も繰り返して安全性を確認してからお薬として売られることになります。この現在においても人間の健康を維持するためのタンパク質の情報というものは全然出揃っていないため、計算だけで副作用のない薬を作るということは不可能です。少なくとも完璧な人体構造シミュレータが生まれるまでは計算だけで安全な薬を作るというのは不可能でしょう。
計算による創薬に話を戻しますが、計算による現在の主流な創薬方法は2つに分かれます。1つはLigand-based drug design(LBDD)と呼ばれる手法、もう1つはStructure-based drug design(SBDD)の手法です。それぞれの特長をさっくりまとめてみます。
| LBDD | SBDD | |
|---|---|---|
| 代表的な手法 | 機械学習 QSAR pharmacophore |
MDシミュレーション ドッキングシミュレーション |
| Pros |
ヒット率が高い (比較的)計算コストが低い |
新規構造骨格を持つ化合物を見つけやすい 生化学的な変異体による活性変化のデータ参照も可能 |
| cons | 既知の阻害剤(データセット)がないと苦しい | タンパク質構造情報がないと苦しい |
新しい薬候補を見つけてくるのであれば、圧倒的にLBDDの方が楽です(タブンネ)。ただし、これは過去の阻害剤データに依存しているために1から阻害剤を見つけ出すのには向いていません。SBDDの方は構造情報をダイレクトに用いるので、相互作用エネルギーを計算してエネルギースコアを算出させたり、生化学的な実験データと照らし合わせて、「このアミノ酸が重要なはずなのにこの阻害剤候補とは結合していない、エネルギースコアは良いけれどたぶん間違いだろう」というような判定もすることができます。しかし実際にはLBDDの方が概してヒット率は高いです。その理由を含めて次の項で紹介します。
タンパク質の構造変化
上の図でタンパク質の絵を紹介しましたが、実際にはタンパク質はナノスケールの分子であり、周囲の水分子の影響や熱運動で常時プルプル振動しています。さらにタンパク質は剛体から程遠い物質なので、タンパク質の結晶構造はとある1つの状態でしかありません。ほとんどの場合において、結晶構造はそのタンパク質の持つ安定構造の1つですが、同時に、往々にして別の安定構造を(場合によっては複数)持っており、この状態間の構造変化を用いて化学反応を触媒しています。つまり化合物がはまるくぼみも常時変化しているのです。 これがSBDDでなかなか薬候補を見つけてくるのが難しい原因の1つです。
ここで、この構造変化をシミュレートするのが分子動力学(MD)シミュレーションです。私の専門分野です。薬候補の化合物と一緒にタンパク質のシミュレーションをやってみて、化合物とタンパク質がくっついたままでさらに結合エネルギーを計算してみても良い値を示していれば見込みがあります。しかしすぐに解離していったりするのであればよくなさそうということです。
ですが、このMDシミュレーションは現状の技術では2フェムト秒($2 \times 10^{-12}$秒)ずつしか時間を動かすことができず、マイクロ秒オーダー($10^{-6}$秒)のシミュレーションがせいぜいといったところです。まあこれでも10年前は100ナノ秒($10^{-7}$秒)で「ヴォースゲー」だったので、それがこの10年で10倍に伸びたというのはすごいことです。しかし、タンパク質の構造変化を十分にサンプリングするためには100マイクロ秒とか、場合によってはミリ秒まで欲しい所です。なので、1化合物に対して1マイクロ秒までは時間をかければできなくはないですが、あと100倍以上の時間が実際には必要ですし、そもそも大量の化合物があるので、実用という面で言えばもう少し技術発展を待ちたいところです。時代が追いつけば強力になるんですけどね。最近流行りの機械学習の昔と今みたいな感じで。
構造変化を加速させるMDシミュレーションの計算手法の開発
というわけで、エライ計算科学者、物理学者の方々はなんとかして物質(タンパク質を含む)の構造変化を加速させ、他の安定構造を探る方法をいくつか考案してきました。今日紹介するAccelerated MDの手法はその1つです。では見ていきましょう。
Accelerated MDの概要
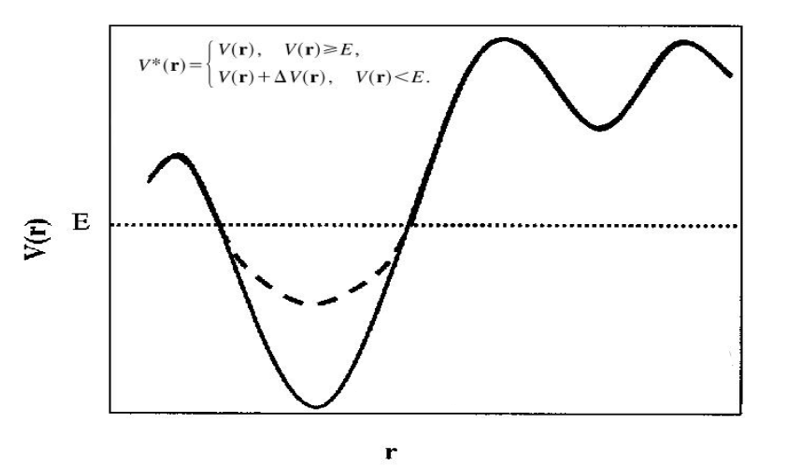
Acclerated Molecular Dynamics (以降aMDとも)は、系の異なる状態を隔てるエネルギー障壁の高さを小さくすることでコンフォメーショナルサーチのサンプリングを改善するための手法です。この手法ではポテンシャルエネルギーランドスケープ(potential energy landscape)のうち、一定のエネルギー値以下のエネルギーのくぼみ(well, basin)に対して一定の補正をかけることでくぼみを「浅く」し、一定のエネルギー以上に対しては何も補正をかけない、というのが原則です。結果として近傍のエネルギーくぼみを隔てるエネルギー障壁は小さくなり、これまでのふつうのMDシミュレーションでは簡単に探索しきれなかった構造空間をサンプリングすることができるようになります、というものなんだってさ。
aMDはAMBERとNAMDにすでに実装されており、このソフトを持っている人は簡単に設定することができます。リファレンスはこちら↓
Accelerated Molecular Dynamics: A Promising and Efficient Simulation Method for Biomolecules, D.Hamelberg, J.Mongan, and J.A. McCammon. J. Chem. Phys., 120:11919-11929, 2004.
Implementation of Accelerated Molecular Dynamics in NAMD, Y.Wang, C.Harrison, K.Schulten, and J.A. McCammon, Comp. Sci. Discov., 4:015002, 2011.
理論的背景
物理学的な説明いきます。
オリジナルのaMD論文によれば、ある系のポテンシャルエネルギーが設定したしきい値のエネルギー値$ E$以下になったとき、以下の式に従って、「ブーストポテンシャル」を加えることにして本来のポテンシャルエネルギー$ V({\bf r})$を補正して$ V^*({\bf r})$にさせます。
V^*({\bf r})= V({\bf r}) + \Delta V({\bf r})
ここで $ \Delta V({\bf r})$ はブーストポテンシャルで
\Delta V({\bf r})= \left\{ \eqalign{
0\quad \quad \quad & V({\bf r}) \ge E \cr
{{(E - V({\bf r}))}^2 \over {\alpha + E - V({\bf r})}}\quad & V({\bf r}) < E \cr} \right.
このしきい値エネルギー(threshold energy)$ E$はこの値以下のポテンシャルエネルギーに対してブーストをかける規定のしきい値ですが、そのブーストの強度を規定する$ \alpha $のパラメータによって変換後のポテンシャル曲面が決まります。数式を見ればわかるように、$ \alpha $を大きく設定すれば補正$\Delta V({\bf r})$は小さくなるので構造変化はゆるくなります。小さくすればその逆です。ただし$ \alpha $は0に設定することはできないようになっています。ポテンシャル曲面が不連続になってしまうからです。
こうした補正をかけたaMDから、オブザーバブルな物理量$ A({\bf r})$のアンサンブル平均$ \langle A \rangle$は次の式のreweightingによって計算することができます。
\langle A \rangle =\frac{\langle A({\bf r})\,\text{exp} (\beta \Delta V({\bf r})) \rangle^* } {\langle \text{exp} (\beta \Delta V({\bf r})) \rangle^*}
ここで $ \beta=1/k_BT$であり($k_{B}$はボルツマン定数)、$ \langle ... \rangle$と$\langle...\rangle^*$はそれぞれオリジナルのアンサンブルとaMDアンサンブルから得られたアンサンブル平均を表しています。
現在、aMDは "aMDd", "aMDT", "aMDdual"の3モードから選ぶことができます。デフォルトはdihedral potential(二面角ポテンシャル)にブーストをつけるaMDdの手法、全ポテンシャルエネルギーに対して適用するaMDTの手法、二面角と全ポテンシャルエネルギー両方につけるaMDdualの手法です。最後の手法では二面角ポテンシャルエネルギーに対するブーストと、(全ポテンシャル - 二面角ポテンシャル)エネルギーに対するブーストを独立にかける仕組みになっています。
Procedure(by AMBER Advanced tutorial 22より)
理論ばっかりじゃあわからないので、分子動力学シミュレーションソフトAMBERに実装されているaMD機能を使ってやってみましょう。
元はAMBER Advanced Tutorial 22に書かれてある方法から。
前準備
対象となるタンパク質のMD開始準備をします。ここは例によってタンパク質のトポロジーファイル生成 → 系の最小化 → NVT平衡化 → NPT平衡化(10ns程度)すれば良いです。
タンパク質の分子シミュレーションをやったことがあるヒトなら上の説明でわかると思います。
Accelerated MDの開始とデータコレクション
上記手順でとりあえずタンパク質の平衡化された構造が得られたら、次の計算パートでは、aMDパラメータを開始するのに必要なパラメータの情報を集めるために短い通常MDシミュレーションを行います。
globularタンパク質の場合
AMBER tutorial 22では次の計算式でパラメータを決めていました。
\eqalign{
a)\,\,{\rm{EthreshP}}:{E_{{\rm{total}}}} = & V_{\rm{total\_avg}}+0.16*N_{\rm{atoms}} \cr
b)\,\,{\rm{alphaP}}:{\alpha _{{\rm{total}}}} = & 0.16*N_{\rm{atoms}} \cr
c)\,\,{\rm{EthreshD}}:{E_{{\rm{dih}}}} = & V_{\rm{dih\_avg}}+4*N_{\rm{residues}} \cr
d)\,\,{\rm{alphaD}}:{\alpha _{{\rm{dih}}}} = & 0.2 *4*N_{\rm{residues}} \cr}
リラックス構造の短い時間でのNormal Production Runで平均のtotal potential energyがおよそ$-47,128\ {\rm kcal/mol}$で平均の dihedral energyが$595\ {\rm
kcal/mol}$であったとする。この情報と今回用いている蛋白質BPTIが58残基 (solute residues)で全体が18,226原子数であることを考えて、次のようにaMDパラメータを計算します。
\eqalign{
a)\,\,{\rm{EthreshP}}:{E_{{\rm{total}}}} = & - 47128\,{\rm{kcal\,mol}^{ - 1}} + (0.16\,{\rm{kcal\,mol}^{ - 1}}\,{\rm{atom}^{ - 1}}*18,226\,{\rm{atoms)}} = - 44212\,[{\rm{kcal\,mol}^{ - 1}}] \cr
b)\,\,{\rm{alphaP}}:{\alpha _{{\rm{total}}}} = & (0.16\,{\rm{kcal\,mol}^{ - 1}}{\rm{atom}^{ - 1}}*18,226\,{\rm{atoms}}) = 2916\,[{\rm{kcal\,mol}^{ - 1}}] \cr
c)\,\,{\rm{EthreshD}}:{E_{{\rm{dih}}}} = & 595\,{\rm{kcal\,mol}^{ - 1}} + (4\,{\rm{kcal\,mol}^{ - 1}}\,{\rm{residue}^{-1}}*58\,{\rm{solute}}\,{\rm{residues}}) = 827\,[{\rm{kcal\,mol}^{ - 1}}] \cr
d)\,\,{\rm{alphaD}}:{\alpha _{{\rm{dih}}}} = & (1/5)*(4\,{\rm{kcal\,mol}^{ - 1}}\,{\rm{residue}}{{\rm{s}}^{ - 1}}*58\,{\rm{solute}}\,{\rm{residues}}) = 46.4\,[{\rm{kcal\,mol}^{ - 1}}] \cr}
膜タンパク質の場合
ここの値の算出方法は系によって様々であり、例えばGPCRの一種のCRFR1についてのaMDシミュレーションでは以下のように計算していました。
\eqalign{
a)\,\,{\rm{EthreshP}}:{E_{{\rm{total}}}} = & V_{\rm{total\_avg}}+0.2*N_{\rm{atoms}} \cr
b)\,\,{\rm{alphaP}}:{\alpha _{{\rm{total}}}} = & 0.2*N_{\rm{atoms}} \cr
c)\,\,{\rm{EthreshD}}:{E_{{\rm{dih}}}} = & V_{\rm{dih\_avg}}+\lambda*V_{\rm{dih\_avg}} \cr
d)\,\,{\rm{alphaD}}:{\alpha _{{\rm{dih}}}} = & \lambda*V_{\rm{dih\_avg}} /5 \cr}
ここで$N_{\rm atoms}$は系の総原子数、$V_{\rm{dih\_avg}}$と$V_{\rm{total\_avg}}$はそれぞれ150 nsのnormal MDシミュレーションから得られた平均dihedralとtotal potential energies (後述のAMBERのアウトプットログファイルにおけるDIHEDとEPtotの値に相当します), $\lambda$は加速するときの変更可能なパラメータとして設定してあります。Miao et.alの論文によればM2 muscarinic receptorの活性化のときには$\lambda = 0.3$が選ばれていました。しかしこれは一例であり、予備実験として$\lambda = 0.2, \cdots, 0.4$で条件を振って50 nsのaMDをそれぞれやってみて、観測したいコンフォメーション変化の具合と二次構造αヘリックスの崩壊具合(ともに$\lambda$が大きいほど加速する)のバランスの良い点を探すことも推奨されます。
NPT平衡化するところまではGROMACSでも良いかもしれません。dihedralとtotal potential energyは当然ながらGROMACSのlogファイルにも記述されているので、kJ/molとkcal/molの単位にさえ気をつければ、ファクター4.184で相互変換できます。
GROMACSのlogファイル例は
Step Time
135000 270.00000
Energies (kJ/mol)
Bond Restraint Pot. U-B Proper Dih. Improper Dih.
2.09000e+04 3.41251e+01 1.00328e+05 7.48014e+04 1.52031e+03
CMAP Dih. LJ-14 Coulomb-14 LJ (SR) Coulomb (SR)
-6.98692e+02 1.46477e+04 -5.92555e+04 7.98060e+04 -1.71899e+06
Coul. recip. Potential Kinetic En. Total Energy Temperature
3.29195e+03 -1.48361e+06 3.88874e+05 -1.09474e+06 3.09170e+02
Pressure (bar) Constr. rmsd
-1.98937e+02 3.95036e-06
AMBERのlogファイル例は
NSTEP = 100000 TIME(PS) = 200.000 TEMP(K) = 308.67 PRESS = 5.0
Etot = -263476.0248 EKtot = 92794.5312 EPtot = -356270.5561
BOND = 5298.8549 ANGLE = 18596.1196 DIHED = 18064.7875
UB = 6425.7921 IMP = 386.7631 CMAP = -166.8393
1-4 NB = 3559.2544 1-4 EEL = -14262.4047 VDWAALS = 15825.9460
EELEC = -409998.8297 EHBOND = 0.0000 RESTRAINT = 0.0000
EKCMT = 31614.6714 VIRIAL = 31463.5317 VOLUME = 1387232.1856
Density = 1.0278
------------------------------------------------------------------------------
GROMACSのProper Dih.とPotential、AMBERのDIHEDとEPtotが4.184倍すればだいたい同じになっているはずです。
実例
系の原子数$N_{\rm atom} =
142855$のCRFR1についてのシミュレーションで試してみました。系の全体total
potential energy$V_{\rm{total\_avg}}$とdihedral energy$V_{\rm{dih\_avg}}$はAMBERで150 nsほどNPTシミュレーションを行い、その平衡化した値から取得しました。それぞれ$V_{\rm{total\_avg}}
= -356270 \,[{\rm{kcal\,mol}^{ - 1}}]$と$V_{\rm{dih\_avg}} =
18045\,[{\rm{kcal\,mol}^{ - 1}}]$であったことから、$\lambda =
0.3$として以下のような設定ファイルamd.inを作製しました。
vt-continue
&cntrl
imin=0, ! Molecular dynamics
irest=0, ! DO NOT restart MD simulation from a previous run.
ntx=1, ! Coordinates and velocities will not be read
! irest=1, ! Restart MD simulation from a previous run.
! ntx=5, ! Coordinates and velocities will be read from a previous run.
nstlim=1000000, ! Number of MD steps
dt=0.002, ! Timestep (ps)
ntc=2, ! SHAKE on for bonds involving hydrogen atoms
ntf=2, ! No force evaluation for bonds with hydrogen
ig=-1, ! Random seed for Langevin thermostat
cut=10.0, ! Nonbonded cutoff (Angstroms)
tol=0.000001 ! SHAKE tolerance
ntb=2, ! Constant pressure periodic boundary conditions
ntp=2, ! Anisotropic pressure coupling
ntpr=5000, ! Print to mdout every ntpr steps
ntwr=500000, ! Every ntwr steps during dynamics, the "restrt" file will be written
ntwx=5000, ! Write to trajectory file every ntwc steps
ntt=3, ! Langevin thermostat
gamma_ln=2.0, ! Collision frequency for thermostat
temp0=310.0, ! Simulation temperature (K)
ioutfm=1, ! Write binary NetCDF trajectory
iwrap=1, ! the coordinates written to the restart and trajectory files will be "wrapped" into a primary box.
iamd=3, ! boost the whole potential with an extra boost to the torsions
ethreshp=-313413.50, alphap=42856.5,
ethreshd=23458.5, alphad=1082.7,
/
&ewald
dsum_tol=0.000001,
/
また実行ファイルrun.shは以下の通り(AMBER GPU版の pmemd.cuda.MPIを使用)
# !/bin/sh
# PBS -l select=1:mpiprocs=36
# PBS -l walltime=48:00:00
cd $PBS_O_WORKDIR
. /etc/profile.d/modules.sh
module load cuda/8.0.44
export AMBERHOME="/path/to/apps/amber16"
export LD_LIBRARY_PATH="/path/to/apps/openmpi-2.1.1/lib:/path/to/apps/gcc-5.4.0/lib:/path/to/apps/gcc-5.4.0/lib64:$LD_LIBRARY_PATH"
export PATH="/path/to/apps/openmpi-2.1.1/bin:/path/to/apps/gcc-5.4.0/bin:$PATH"
$AMBERHOME/bin/pmemd.cuda.MPI -O \
-i amd.in \
-o md.out \
-p /path/to/ambertopology.parm7 \
-c /path/to/amberconventionalMD/mdCRFR.rst7 \
-r amdCRFR.rst7 \
-ref /path/to/ambertopology.crd
-pはトポロジーファイル、-cはcontinueする直前のリスタートファイル(AMBER rst7形式)、-rはこのaMD内で定期的に書き出すリスタートファイル、-refはリファレンスとする座標ファイル。AMBERのconventional MD(いわゆる普通のMD)で150 nsほど計算した最後のリスタートファイルを/path/to/amberconventionalMD/mdCRFR.rst7とし、-cオプションに投入しました。
Reedbush-Hで動かす場合、mpirunを使って2ノード以上設定すると全然速度が出なかった(設定が悪かった?)。ふつうに1ノードで上記設定をした方が良いってか下手したらGROMACSより計算速度出てるような。
応用例と結果
以下にAccelerated MDシミュレーションの結果例を示しています。
膜タンパク質の場合
私がやってみたとあるGPCRタンパク質CRFR1(結晶構造からミッシング残基を補完している)ではこんな感じになりました。
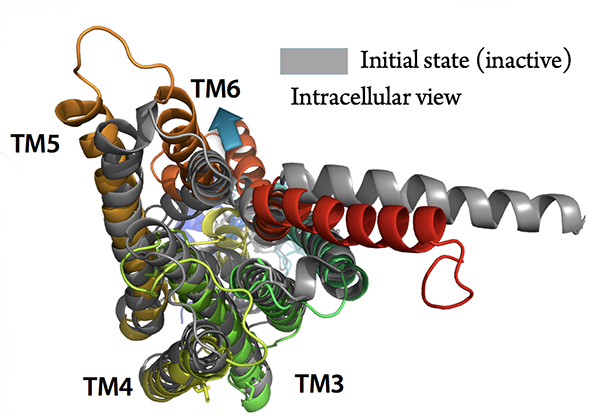
class B GPCRだとTM6が大きく外側に動いてパカっと開き、その空いた隙間にGタンパク質が突っ込んでくることが近年わかってきました。しかしこの構造変化は通常のMDシミュレーションの時間ではなかなか観測することができません。しかしaMDでその様子を観測することができました。この結果については2015年に論文化されていましたので、それも参考になると思います。
超長時間サンプリングしたふつうのMDとaMDの構造空間探索結果の比較
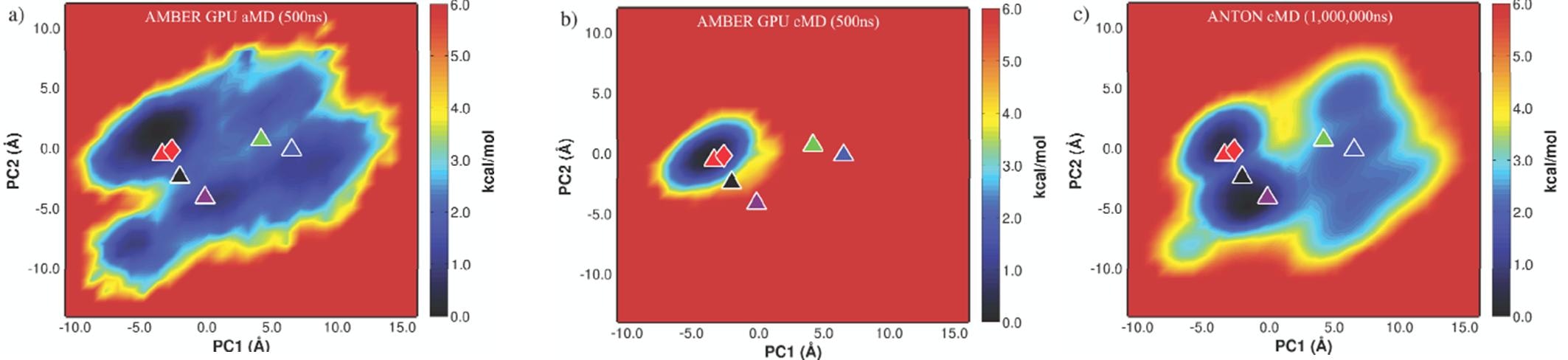
構造空間の探索結果を図で表すのに主成分分析(PCA)で表すことがよく行われますが、超長時間やってみたときのふつうのMDの結果と、aMDの結果を比較したものがさっきのAMBER Tutorial 22に紹介されてあります。
真ん中がconventional MD、つまりふつうのMDを500ナノ秒やってみたときの結果、右は世界最強最速のMD専用マシンANTONが1ミリ秒(1,000,000ナノ秒)やってみた結果です。500 nsでは構造空間の探索がまだまだ不十分であることがわかります。しかしaMDの結果(図左)では同じ500 nsでANTONが1ミリ秒内に探索できた構造空間を結構カバーできていることがわかります。aMDスゴイかもしれない……!?
あ、ちなみにANTONはアメリカの超大金持ちのD.E. Shawさんの個人的な趣味で作った特注品です。2017年の東大のスパコン(Intel Xeon + GPU NVIDIA P100*2)を使って僕らが現実的に出せる計算速度よりも、2008年に稼働したこれは数百倍以上計算速度が出てます。2014年にはANTON 2が出ました。(ヾノ・∀・`)ムリムリ その代わり、このANTONはMD以外の計算にはまったく使えない(汎用性がない)らしいんですけどね。
総括
今回はAccelerated MDによるタンパク質のコンフォメーショナルサーチを効率的に行う方法を紹介しました。使いみちとしては以下の様なものが考えられます。
- 既知のホモログタンパク質から類縁のタンパク質をホモロジーモデリングで作り出したあと、そのタンパク質の最安定構造を速やかに取り出す
- 安定な状態を複数持つフレキシブルなタンパク質(膜タンパク質など)の構造変化を加速させる
- タンパク質のフォールディングシミュレーションもいけるか?
Accelerated MDはGROMACSに実装されていなかったため、今回はAMBERを使うことになりました。NAMDにも同じアルゴリズムで実装されています。ところで、最近リリースアナウンスがあったGROMACS 2018ではこれと似たような新規な効率良いコンフォメーショナルサーチ法を実装したそうです。これがどんなものか自分が理解できたらそれについても書こうと思います。