#はじめに
異なるトポロジー・頂点数のメッシュ間をある程度狙って補間して変形する方法の考え方を説明する記事です。
アバターや3Dモデルを合成するツールを作ったはいいものの、色々と規約的にも倫理的にも面倒が多そうなので開発をストップすることにしました。
方法だけ記事に残しておくので気になる人は頑張って製作してみてください。できるだけ多くの人が分かるように優しく書いたつもりです。
実際のプログラムの実装に関する細かい話には最後の注意点以外では触れていません。
#知識の下準備
###「頂点数が等しいこと」の必要性
2つのメッシュの頂点数が等しい場合、頂点間で１対１で対応付けすることが出来るため、補間が容易になります。補間を行うことが出来るということは、相互に変換ができるということとほぼ等しいです。
例えば正三角形と直角二等辺三角形は頂点数が等しいため、相互変換（補間）を容易に行えます。
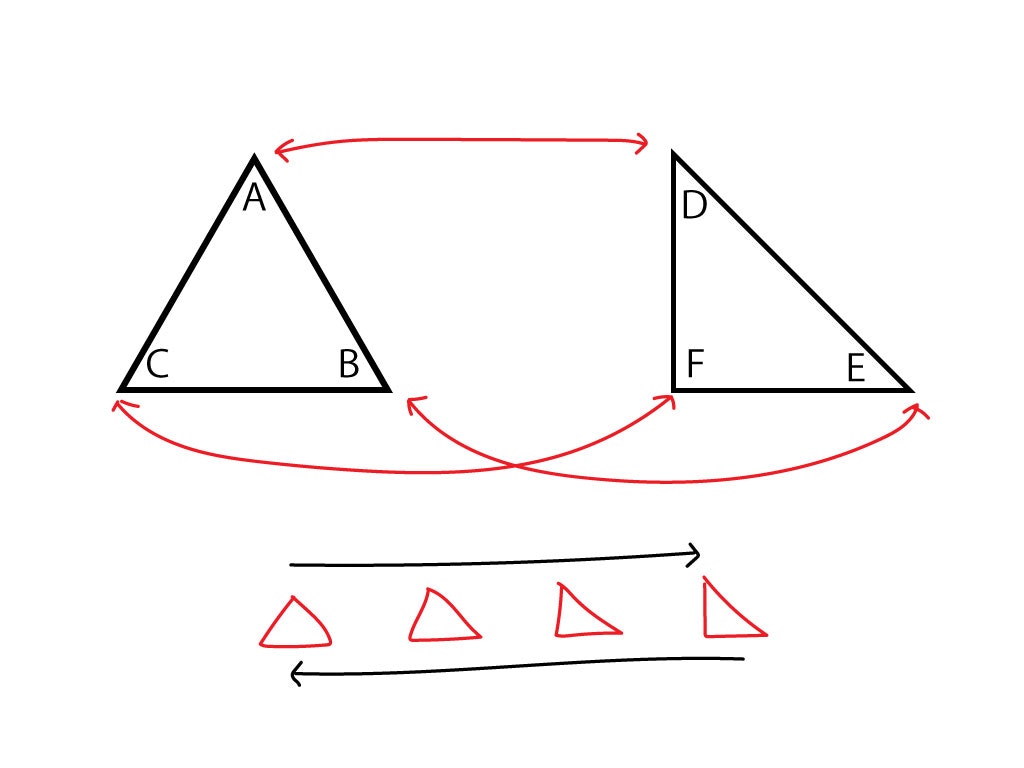
しかし正三角形と正方形は頂点数が異なるため、対応付けの段階で悩むことになります。
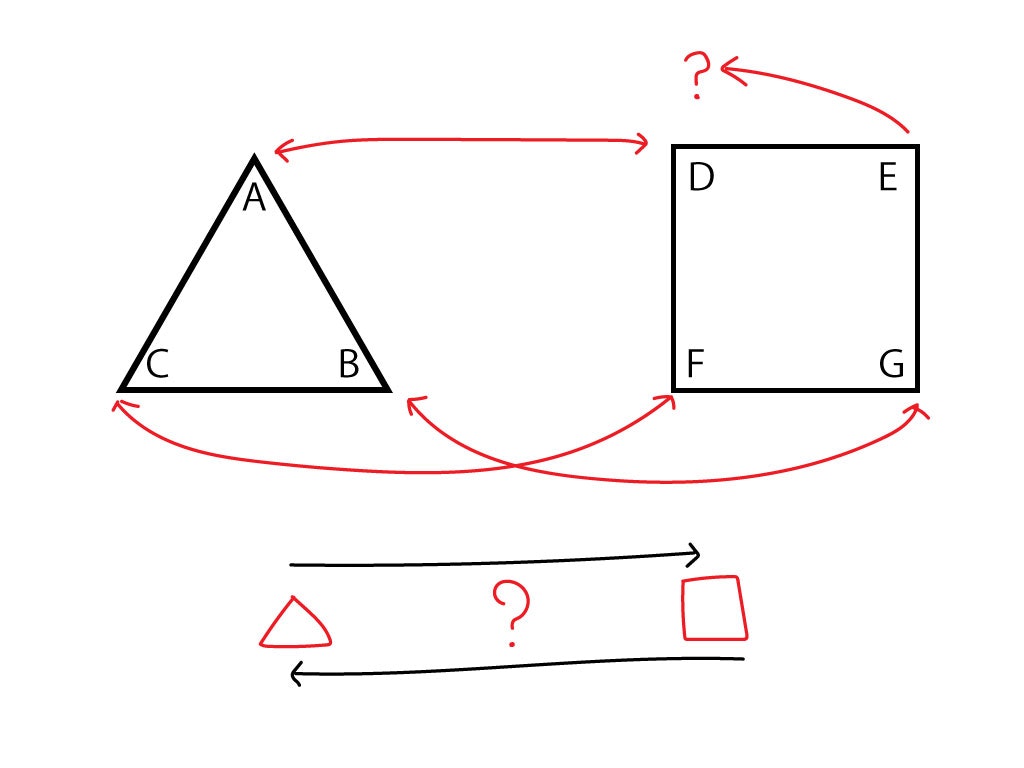
正三角形の角Aと角Bの間に頂点を作り、それを正方形の角Eと対応づけることで相互変換を行うこともできます。しかし、この例では頂点数が3,4つと少ないためまだ対応付けをすることが出来ますが、頂点数が数千、数万と増えてくるとこの操作をすることはほぼ不可能でしょう。
形が全く違う場合どの頂点の間に新しく頂点を作れば良いのか判断が難しく、手動はもちろんプログラムを書いて自動で行うことも非常に困難です。
そのため、通常補間を行うには2つのメッシュの頂点数が等しいことが必須となります。
###「頂点の順番が等しいこと」の必要性
実は「頂点数が等しい」だけでは補間を行うことは困難です。
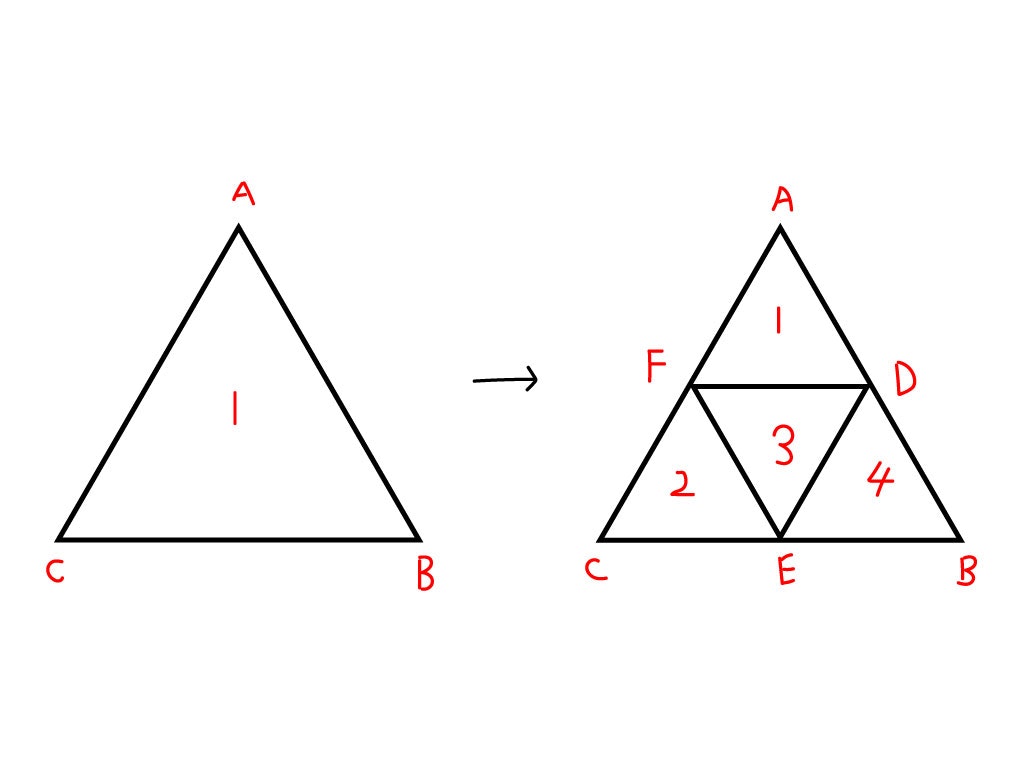
上の正三角形と直角二等辺三角形の例ではAとD、BとE、CとFが対応していると多くの人が考えると思います。しかしこれをプログラムで判定することはとても難しいです。
どうやって私たちはこの組み合わせであると判断したのでしょう。
重ねたときに最も近い頂点？重心から右回りの順番？重心からの距離の順番？
どれも場合によって正確な（私たちが考えるような）結果を出力することができますが、別の場合では正しくない結果を出力します。私たちは図形を見て適切な対応付けの方法を選択することが出来ますが、機械がそれを行うことは困難です。
そこで、あらかじめ頂点のデータ上の順番を私たちが考えるような結果になるように並び替えておきます。すると2つのメッシュのそれぞれ同じ順番の頂点同士を対応づけることができ、どんなに複雑な形状でも私たちが考えた通りに補間することが出来ます。
しかし、頂点数が多かったり形状が複雑な場合は私たちもどの頂点が対応しているのか判断することは出来ません。そのため、頂点数は私たちが判断できる程に少ない必要があります。
###異なるトポロジー・頂点数のメッシュを補間するには
ここまでをまとめると、狙ったとおりにメッシュを補間するには
- 頂点数が等しい
- 頂点の順番が等しい（頂点数が少ない）
という必要があります。
異なるトポロジー・頂点数を持つメッシュの補間はそのままでは行うことが出来ません。
そこで2つのメッシュから頂点数と順番の等しいメッシュを生成してそれの補間を行い、その結果をもとにメッシュを変形させて良い感じに補間変形します。
#補間の下準備
今回説明に使用させていただくのはこちらのCC0のえびふらいと三角コーンです。
###メッシュを簡略化する
まずは変形のベースとなるメッシュを作成します。このメッシュによって変形結果が大きく変わります。
2つのモデルのどこを対応させたいのかを考えながら作成します。
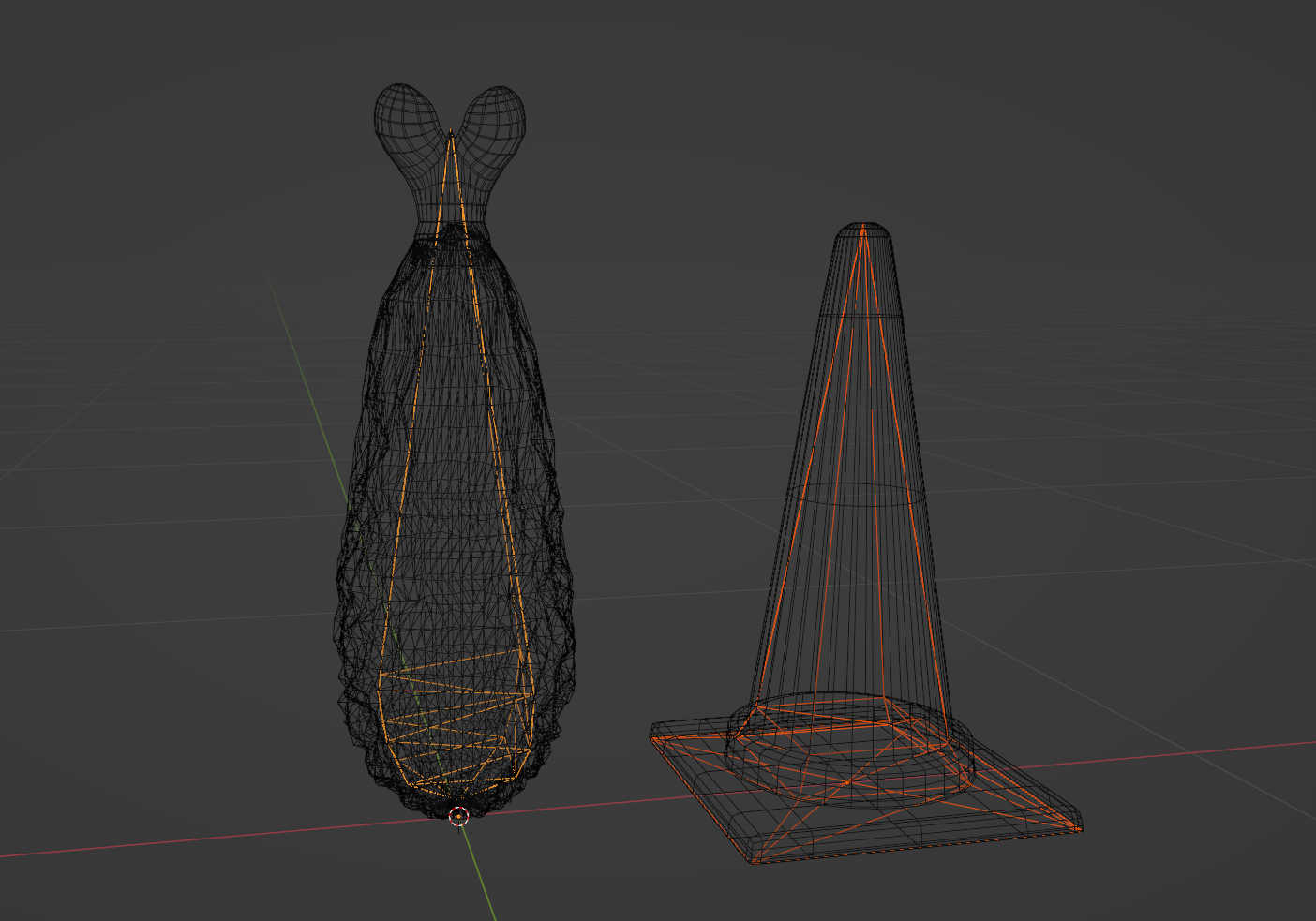
えびふらいの尾の部分が三角コーンの上部と対応するようにメッシュを作成しました。ベースメッシュはもとのモデルにある程度近い形状の方が良い結果になります。
それぞれ14頂点、24三角面です。手動で並び替えができるくらいの頂点数ですね。
ただそれでも頂点を手動で並び替えるのも手間なので、UVを元に頂点を並び替えるプログラムを作りました。2つのメッシュのUVをそろえることで頂点が同じ順番に並び変わります。
これで頂点数と頂点の順番が等しいメッシュができました。これで補間を行うことができます。
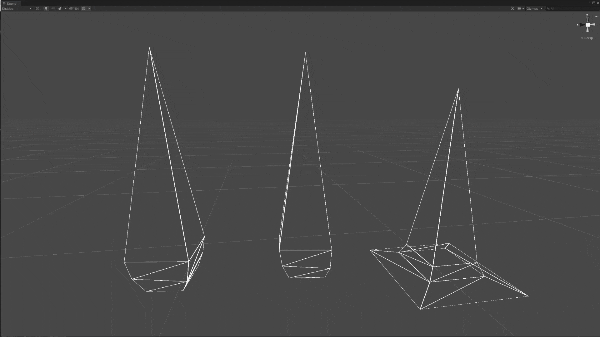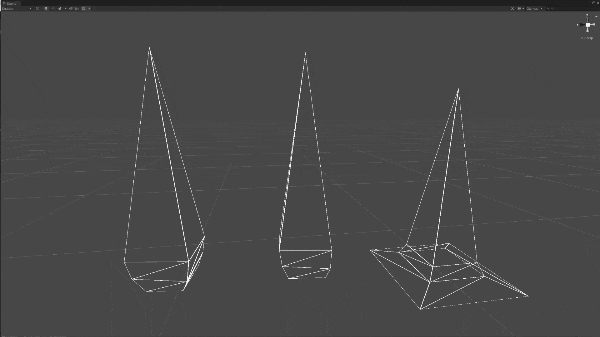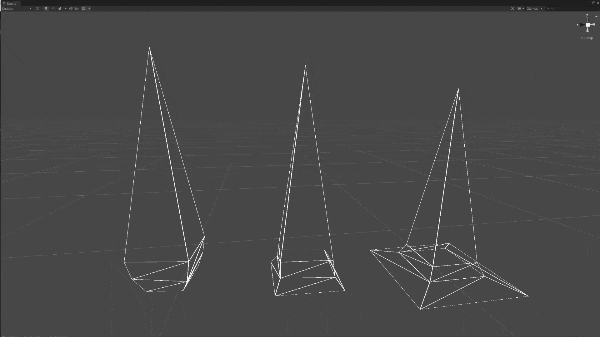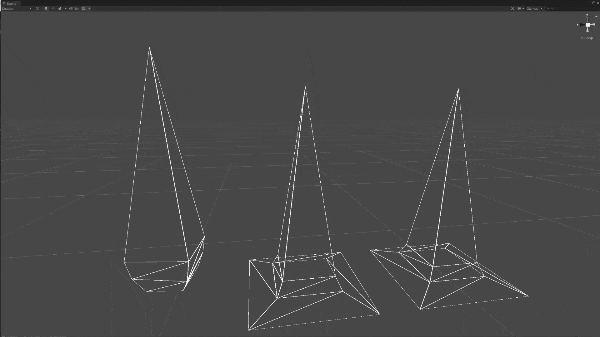
###メッシュの解像度を上げる
このメッシュを元のメッシュに近づけていきます。ここで重要なのが「頂点数が等しい」「頂点の順番が等しい」という条件を崩さずに近づけることです。
これは、三角面を規則的に分割することによって行うことが出来ます。
今回は三角面の辺それぞれの中点を新しい頂点とし、1つの三角形から4つの三角形に分割します。
Blenderの「細分化」が分かる方は、それをイメージすると良いかもしれません。
この操作を一度行うたびに三角面数は4倍に増えます。
しかし、この操作を行うだけでは三角面数が増えるだけで形状は変わりません。
###形状の復元
新しく生成した頂点の位置を調節する必要があります。この方法は色々ありますが今回は特にパフォーマンス等を考慮する必要も無いので、頂点の法線方向に伸びる直線と三角面の交点で最も近い位置を新しい位置とします。
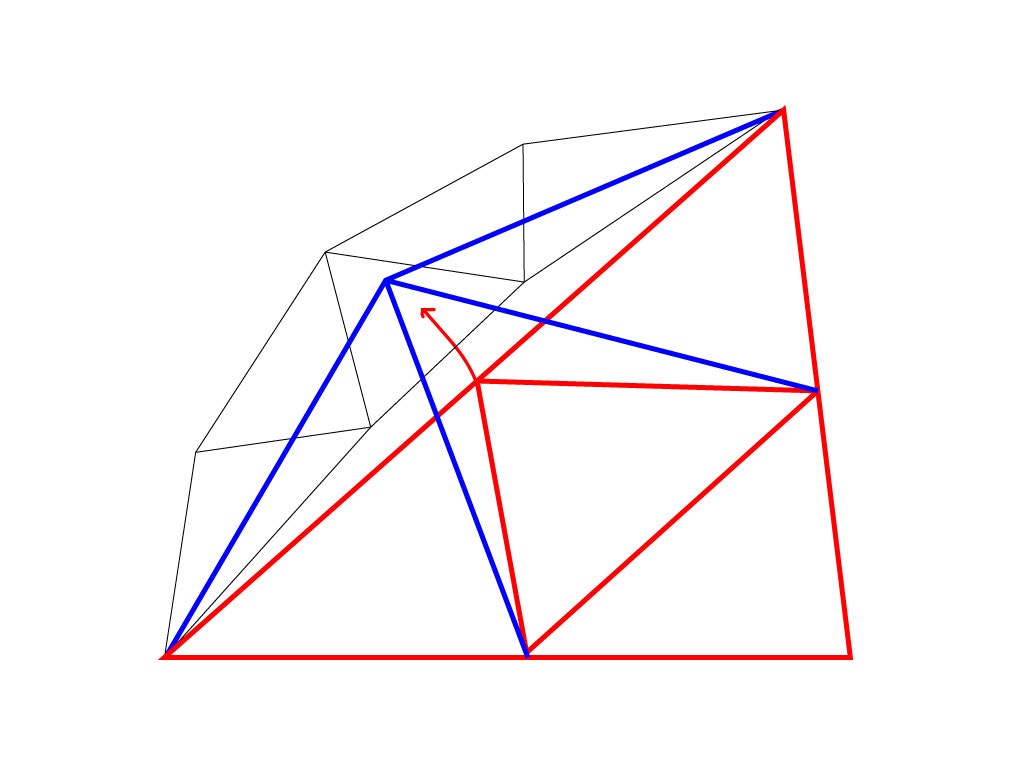黒線がもとのメッシュ、赤線が分割したメッシュ、青線が新しい位置と辺です。要は元々のメッシュに近づける処理を行っているということだけ分かれば大丈夫です。
この方法は形状によっては取得することの出来ない位置がでることがありますが、このメッシュ自体はガイドとして使用して最終的に破棄されるものなので、取れない位置があっても問題ありません。（本当は変換結果には影響するので取得できたほうが良いですが、そこは目的次第です。）
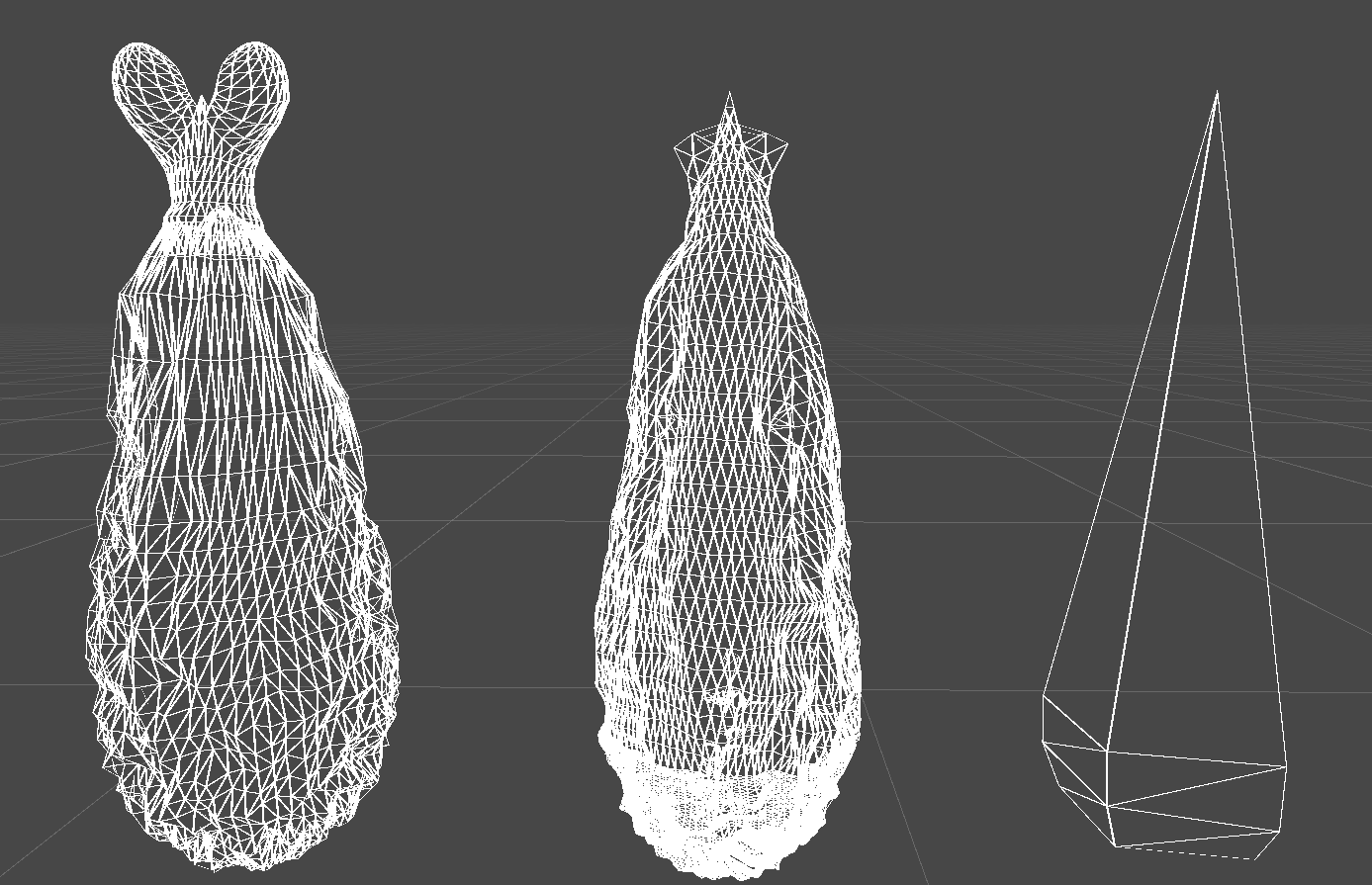大体の形状は取得できていますね。しっぽの部分が細かく形作れていませんが、補間後にしっぽの形を残すためにわざとこの部分が荒くなるようにメッシュを作ったので想定通りです。
分割する回数が多いほど正確な位置になりますが、その分処理にかかる時間が長くなります。
###解像度を上げたメッシュ同士の補間
同じ分割数で解像度を上げたメッシュ同士は頂点数、頂点順番ともに等しいため補間を行うことが出来ます。
これで異なる頂点数のメッシュを補間するためのガイドが完成しました。
ちなみに今回は2つのメッシュで行いましたが、ベースのメッシュ（簡略化されたメッシュ）の頂点数、順番が等しいなら3つ以上のメッシュを混ぜ合わせることも出来ます。
#異なる頂点数の補間変形
ガイドとなるメッシュの生成が終わったら後はガイドと元のメッシュを対応づけることで変形を行うことが出来ます。
###生成されたメッシュと元のメッシュの対応付け
生成されたメッシュ（ガイド）は元のメッシュとほぼ同じ形状をしていて、かつ分割によって元のメッシュよりも細かくなっています。
そのため最も近いガイド内の頂点と、その頂点から元メッシュの頂点への位置ベクトルを保存するだけで対応付けは完了します。
対応付けの方法を変えることによって結果を調整することも出来ます。今回は最近頂点のみですが、最も近い3点ほどを保存した方がより綺麗な補間になると思います。
###補間の逆変換
対応付けが終わったらガイドを補間して好きな形状にしましょう。
その後保存した頂点とベクトルから新たな頂点配列を作成して元のメッシュに入れると補間変形が完了します。
#Unityで実装する場合の注意
Unityで実装する際にはいくつか注意しなければならないことがあります。
###法線/UVの切れ目による頂点増加
同じ位置の頂点でも法線が違うと別頂点と見なされて頂点数が変わってしまうので、ベースメッシュをインポートした時にImportSettingでNormalsをNoneにする必要があります。
またUVの切れ目でも別頂点として扱われてしまうので、ベースメッシュのUVを開く場合はシームの位置もそろえる必要があります。
###Vector3.Normalized()の仕様
細分化の際などとても小さいVector3を扱うことが多いですが、Vector3.Normalized()はそのベクトルがとても小さい場合に0を返すので対策をする必要があります。
私は座標の計算前に値を10万倍にして解決しました。