アルゴリズムの基本

アルゴリズム図鑑が無料公開されていたので、読んでみて自分なりに補足を加えたり、C#やPythonでの追記をして復習をする

アルゴリズムとは?

アルゴリズムとは、数学、コンピューティング、言語学、あるいは関連する分野において、問題を解くための手順を定式化した形で表現したものを言う。算法と訳されることもある。

「問題」はその「解」を持っているが、アルゴリズムは正しくその解を得るための具体的手順および根拠を与える。さらに多くの場合において効率性が重要となる。

コンピュータにアルゴリズムをソフトウェア的に実装するものがコンピュータプログラムである。人間より速く大量に計算ができるのがコンピュータの強みであるが、その計算が正しく効率的であるためには、正しく効率的なアルゴリズムに基づいたものでなければならない。

Wikipediaより引用

上の説明にあるように「問題を解くための手順を定式化した形で表現したもの」である。つまり、数学の○○の定理のように難しい問題を一瞬で解を導いてるれるようなものである。アルゴリズムのすごいところは

• 人が理解できるように記述されていること
• 同じ種類の問題であれば適用できること
• 人手では到底調べ切れない問題を解決できること
• 計算量があらかじめ予測できること

が挙げられる。

アルゴリズムと計算量

計算量とは

アルゴリズムの性能を評価するために、計算量(けいさんりょう)という指標が用いられる。計算量には、時間計算量と空間計算量とがあります。

計算量
時間計算量	理時間がどれだけ掛かるのか
空間計算量	どれだけの記憶容量を必要とするか

計算量のほとんどは時間計算量を指している

O(オーダー)記法

実行環境によって左右される指標ではアルゴリズムの比較をすることが出来ないので、計算量を単純に「3秒かかる」といったような表現をしない。計算量の指標として、「命令数(ステップ数)」を基準とする。

計算量の記述には、O記法という表記が用いられるのが一般的である。

$O(n)$ のように記述し、この場合、データの個数nに比例した時間が掛かることを表している。

記法	詳細
$O(n)$	命令数がデータ数に比例することを意味する
$O(1)$	命令数がデータ数に比例することを意味する n回、もしくは、nに比例する回数以内のループの処理で終わる場合がこれに該当する
$O(n^2)$	計算量の最大次元が $n^2$ であることを意味する 例えば、$2n^2 + 3n + 1$ が該当する $O(n^3)$、$O(n^4)$ といった、より高次のものも同様である
$O(\log n)$	データ数nとするとき、2をステップ数乗した値の定数倍が計算量になるようなアルゴリズム 典型的な例として、二分木などが該当する
$O(n \log n)$	マージソートのように、二分木のようにデータを分割し、かつそれらのデータ全体をリニアサーチするようなアルゴリズムの計算量 二分木のオーダーとリニアサーチのオーダーの掛け合わせになる

二分木探索のオーダー

二分木検索の計算量を考察する。二分木検索は、データ全体をに分割しながら行うサーチである。データとステップ数の関連を表にまとめる

データの大きさ	ステップ数
2	1
4	2
8	3
16	4

$n = 2^{(ステップ数)}$ が成り立つ。つまり、両辺 log をとると $\log n = (ステップ数)$ になる。2分探索の時間計算量は $O(\log n)$ である。

計算量の応用

計算量からわかること

計算量を用いることのメリットは処理時間にある程度の予測が立つことである。O記法で表現すれば、データ数や実行環境に依存すること無くアルゴリズムを比較し、処理時間を見積もることが出来る。

表記	意味	例
$O(1)$	定数	配列を添字アクセスする場合(ex. a[0] = 1;)
$O(\log n)$	対数	二分探索
$O(n)$	一時	線形探索
$O(n \log n)$	$n \log n$	クイックソート
$O(n^2)$	二次	2重ループを伴う配列全体の走査。バブルソートなど
$O(n^3)$	三次	3重ループを伴う配列全体の走査。行列計算など
$O(2^n)$	指数	集合分割問題

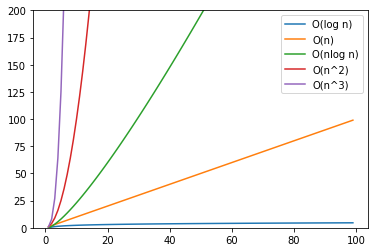
単純に言えば、上の方が計算量の小さい、つまり効率的なアルゴリズムであることを表している。

係数を無視していること、データ数を考慮していないので一部例外がある

import numpy as np
import matplotlib.pyplot as plt

input_data = np.arange(1,100,1)

o_log = np.log(input_data)
o_nlog = input_data * np.log(input_data)
o_n2 = input_data * input_data
o_n3 = np.power(input_data, 3)

plt.plot(input_data, o_log, label="O(log n)")
plt.plot(input_data, input_data, label="O(n)")
plt.plot(input_data, o_nlog, label="O(nlog n)")
plt.plot(input_data, o_n2, label="O(n^2)")
plt.plot(input_data, o_n3, label="O(n^3)")
plt.ylim(0, 300)
plt.legend()
plt.show()

O記法の計算量の比較	nが少ない時の比較

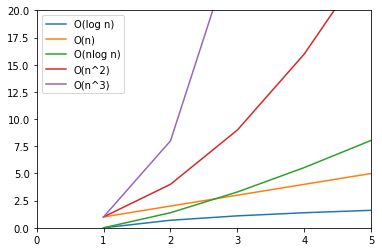係数の比較を付けていないが、$O(n \log n)$ と $O(n)$ は状況によっては効率が入れ替わることがある