予測射撃とは
目標の移動先を狙う撃ち方のことを一般的に偏差射撃と言います。
予測する計算をした射撃に対してイメージが伝わりやすいので予測射撃という言葉を使っています。
この記事では予測射撃沼の入り口の線形予測射撃と円形予測射撃について紹介します。
やりたいこと
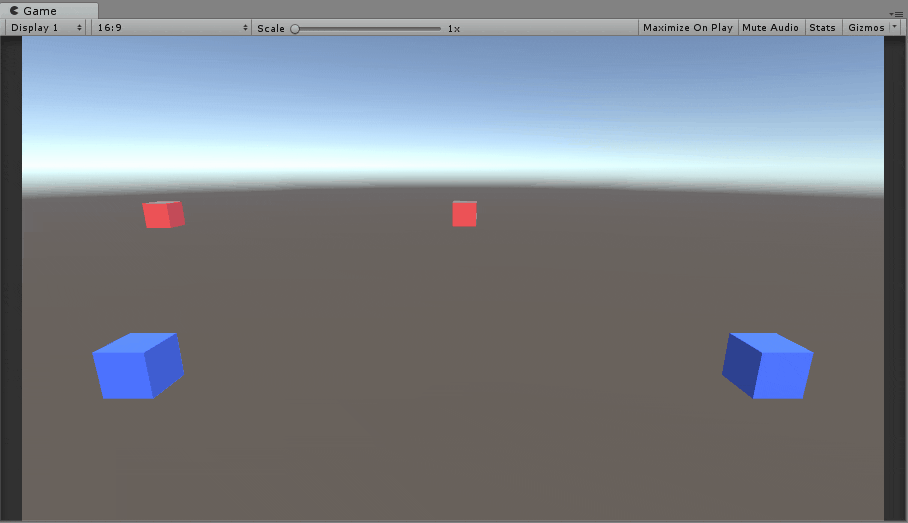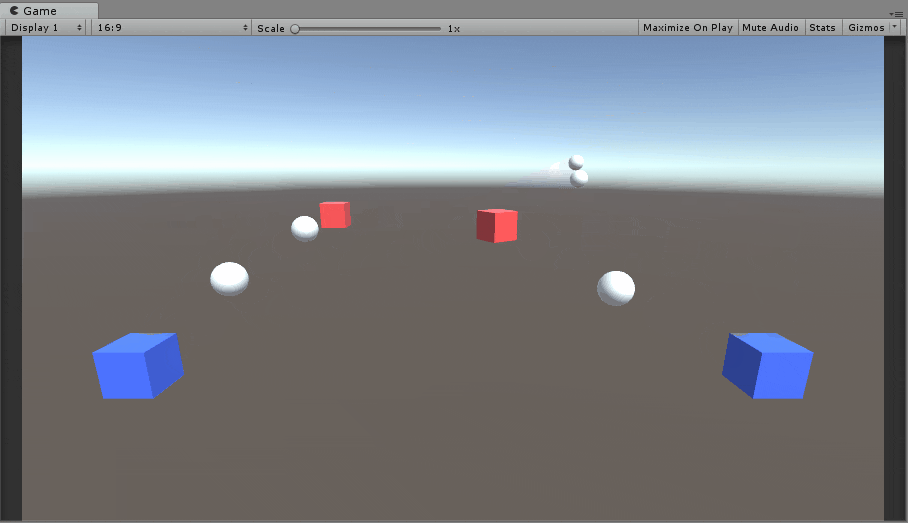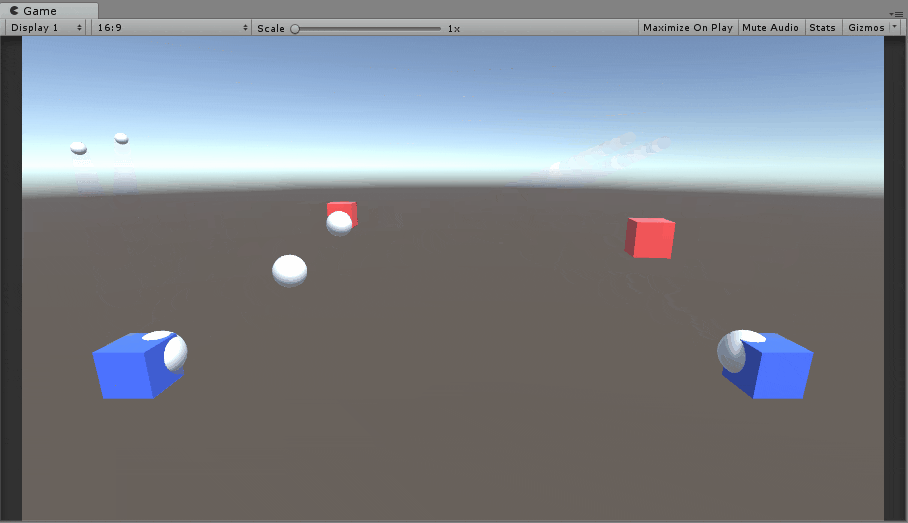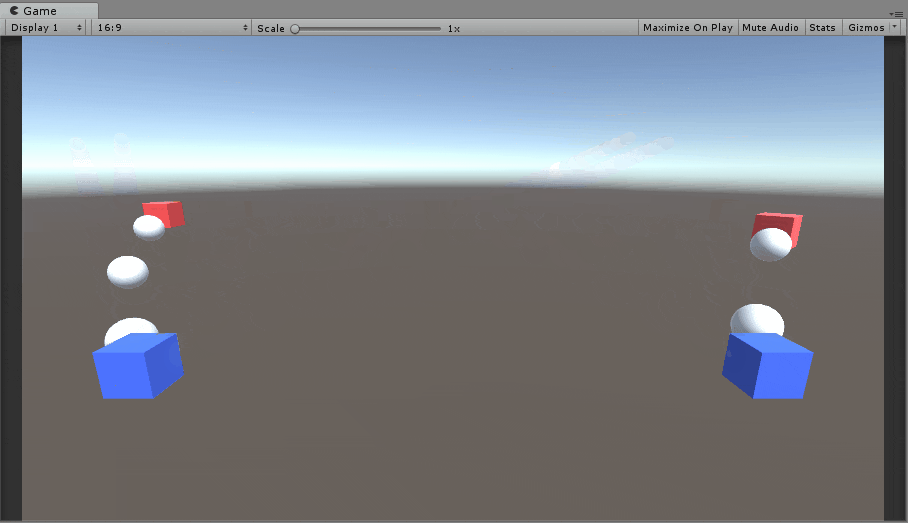
弾を当てるイメージはこんな感じになります。
左は赤い箱がまっすぐ線形移動、右は赤い箱がぐるっと円形移動してます。
線形予測射撃
等速移動している赤丸を青丸の位置から射撃するとします。
まずは全体図を眺めて頂いてから詳細を順番に説明していきます。
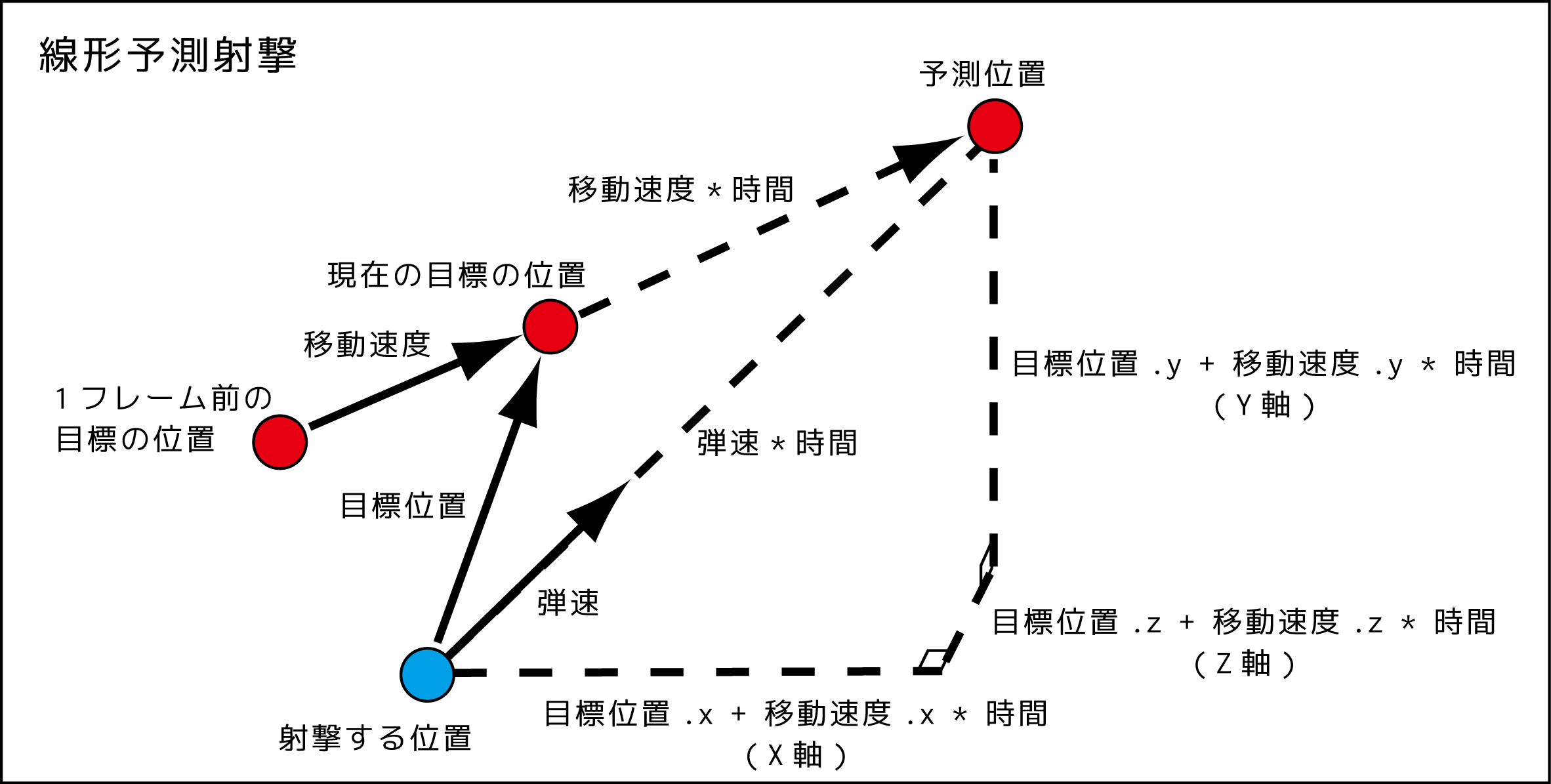
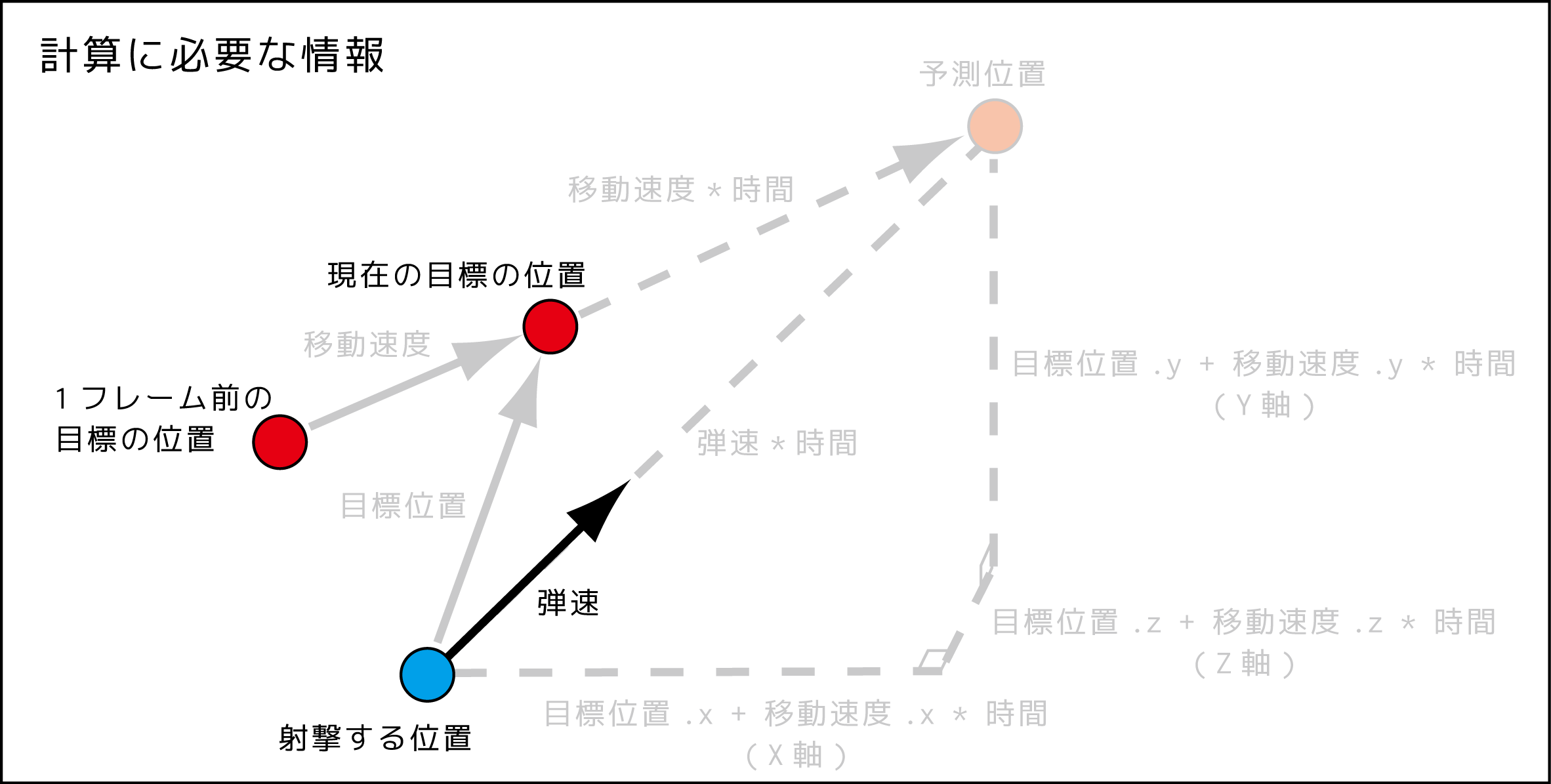
計算に必要な情報は4つ
- 射撃する位置
- 目標の位置
- 1フレーム前の目標の位置
- 1フレームに進む弾の速度
※この記事ではFixedUpdateの1フレームを基準とした時間で計算します。
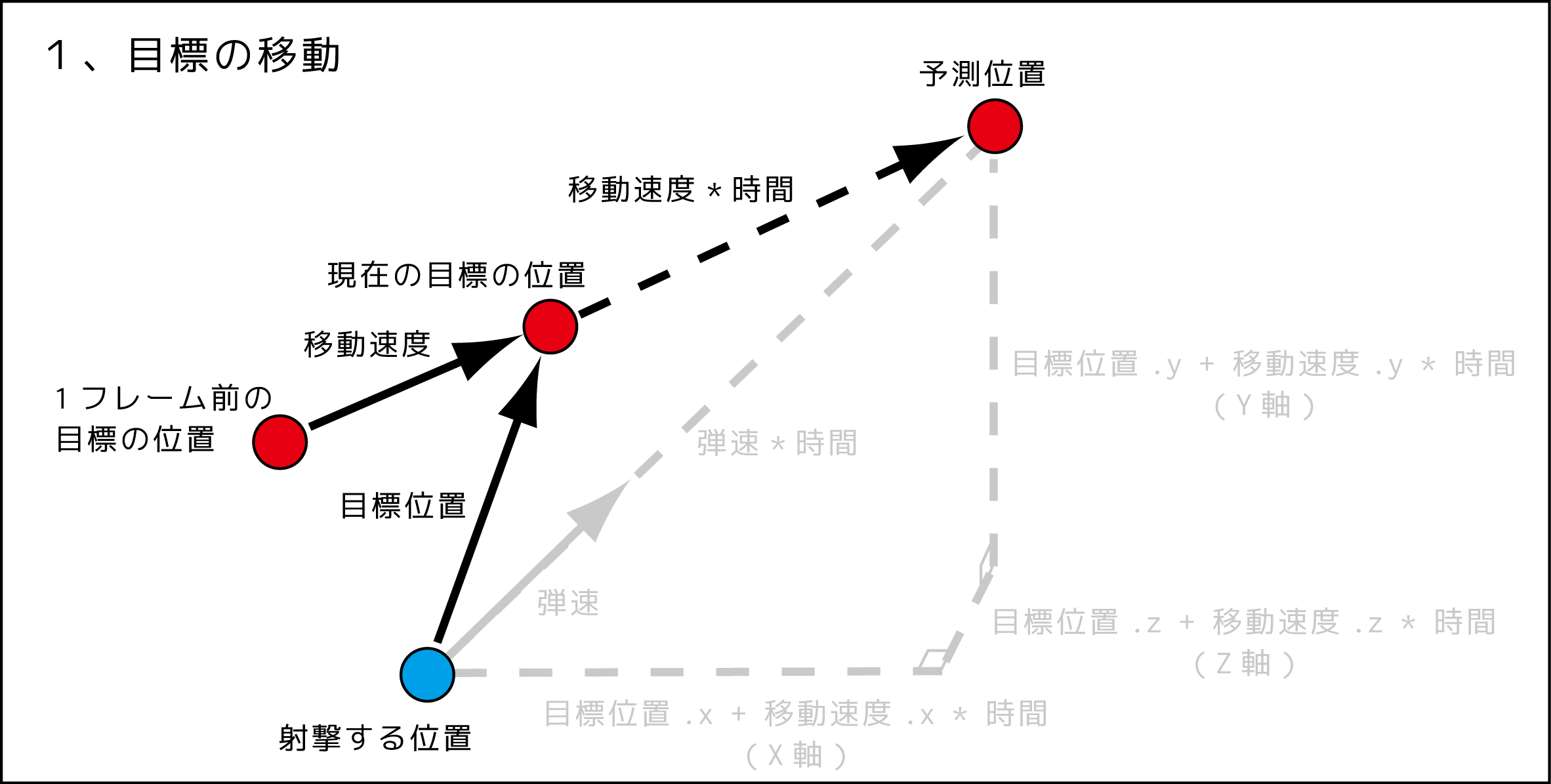
計算手順
1. 目標が移動する場合の式を作る
1フレーム前と現在の差から目標の位置で「移動速度」を出し、
時間が決まれば「$目標位置 + 移動速度 \times 時間$」の位置に移動します。
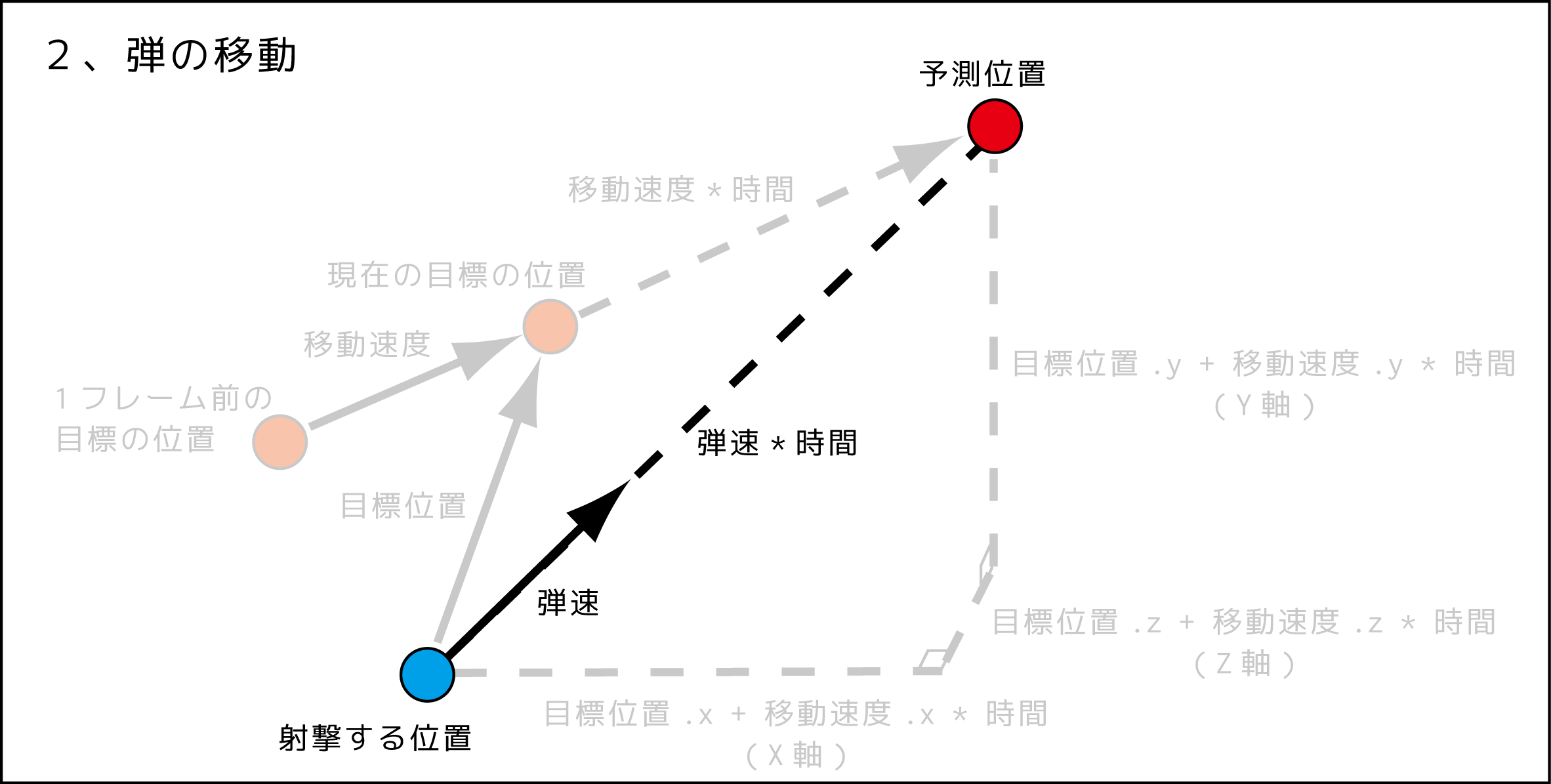
2. 弾が移動する場合の式を作る
時間が決まれば「$弾速 \times 時間$」が射撃する位置から見た距離になります。
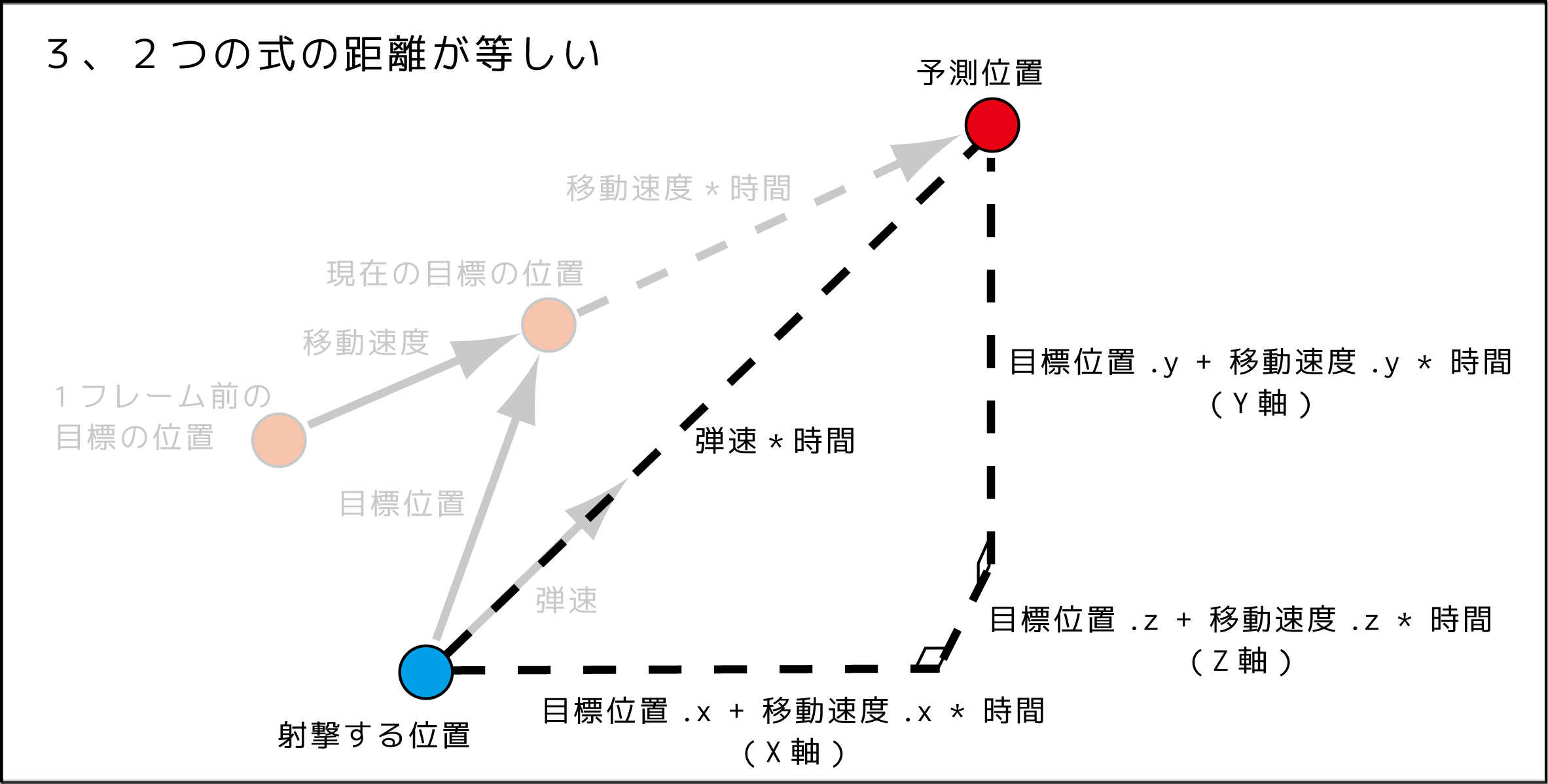
3. 2つの式の距離が等しい式を作る
ピタゴラスの定理を使って2つの式の距離が等しい場合の式を作ります。
この式の解から弾が当たる時間がわかります。
$(弾速 \times 時間)^2 = (目標位置.x + 移動速度.x \times 時間)^2 +(目標位置.y + 移動速度.y \times 時間)^2+(目標位置.z + 移動速度.z \times 時間)^2$
4. 弾が当たる時間を計算する
式を二次方程式の一般形の形にして解の公式から弾が当たる時間を計算します。
二次方程式の一般形:$At^2+Bt+C=0 (t≠0)$の解は、$t=\frac{-B±\sqrt{B^2-4AC}}{2A}$
それぞれの$A、B、C$は下記になるので時間がわかります。
$A = (移動速度.x)^2+(移動速度.y)^2+(移動速度.z)^2 - 弾速^2$
$B = 2 \times (目標位置.x \times 移動速度.x + 目標位置.y \times 移動速度.y + 目標位置.z \times 移動速度.z)$
$C = (目標位置.x)^2+(目標位置.y)^2+(目標位置.z)^2$
5. 弾を撃つべき予測位置を決定する
得られた時間の値で「$現在位置 + 移動速度 \times 時間$」から射撃するべき予測位置を計算します。
解は2つになるので正の数の最小値を採用します。
弾より移動速度が速いと当たらないので虚数解になったり、移動の軸が射撃位置を通過していたりすると0割りするので個別対応が必要になります。
線形予測射撃のスクリプト
//線形予測射撃
public Vector3 LinePrediction(Vector3 shotPosition, Vector3 targetPosition, Vector3 targetPrePosition, float bulletSpeed)
{
//Unityの物理はm/sなのでm/flameにする
bulletSpeed = bulletSpeed * Time.fixedDeltaTime;
//目標の1フレームの移動速度
Vector3 v3_Mv = targetPosition - targetPrePosition;
//射撃する位置から見た目標位置
Vector3 v3_Pos = targetPosition - shotPosition;
//ピタゴラスの定理から2つのベクトルの長さが等しい場合の式を作り
//二次方程式の解の公式を使って弾が当たる予測時間を計算する
float A = (v3_Mv.x * v3_Mv.x + v3_Mv.y * v3_Mv.y + v3_Mv.z * v3_Mv.z) - bulletSpeed * bulletSpeed;
float B = 2 * (v3_Pos.x * v3_Mv.x + v3_Pos.y * v3_Mv.y + v3_Pos.z * v3_Mv.z);
float C = (v3_Pos.x * v3_Pos.x + v3_Pos.y * v3_Pos.y + v3_Pos.z * v3_Pos.z);
//0割り禁止処理
if (A == 0)
{
if (B == 0)
{
return targetPosition;
}
else
{
return targetPosition + v3_Mv * (-C / B);
}
}
//弾が当たる時間のフレームを計算する
float flame1, flame2;
//二次方程式の解の公式の判別式で分類
float D = B * B - 4 * A * C;
if (D > 0)
{
float E = Mathf.Sqrt(D);
flame1 = (-B - E) / (2 * A);
flame2 = (-B + E) / (2 * A);
//解は2つなので正の数の最小値を使う
flame1 = PlusMin(flame1, flame2);
}
else
{
//虚数解
//当たらないので今の位置を狙う
flame1 = 0;
}
//予想位置を返す
return targetPosition + v3_Mv * flame1;
}
//プラスの最小値を返す(両方マイナスなら0)
public float PlusMin(float a, float b)
{
if (a < 0 && b < 0) return 0;
if (a < 0) return b;
if (b < 0) return a;
return a < b ? a : b;
}
自分なりに整理したスクリプト(おまけ)
Bの計算の2を消したり、内積で書いたり、虚数解はどうせ当たらないので絶対値を使って無視してみたりしました。
(内積は掛け算のままで書いた方が速いようですが・・・)
このコードは必要ないかなと迷ったのですが全体がだいぶすっきりしたので張り付けておきます。
//線形予測射撃改良案
public Vector3 LinePrediction2(Vector3 shotPosition, Vector3 targetPosition, Vector3 targetPrePosition, float bulletSpeed)
{
//Unityの物理はm/sなのでm/flameにする
bulletSpeed = bulletSpeed * Time.fixedDeltaTime;
Vector3 v3_Mv = targetPosition - targetPrePosition;
Vector3 v3_Pos = targetPosition - shotPosition;
float A = Vector3.SqrMagnitude(v3_Mv) - bulletSpeed * bulletSpeed;
float B = Vector3.Dot(v3_Pos, v3_Mv);
float C = Vector3.SqrMagnitude(v3_Pos);
//0割禁止
if (A == 0 && B == 0)return targetPosition;
if (A == 0 )return targetPosition + v3_Mv * (-C / B / 2);
//虚数解はどうせ当たらないので絶対値で無視した
float D = Mathf.Sqrt(Mathf.Abs(B * B - A * C));
return targetPosition + v3_Mv * PlusMin((-B - D) / A, (-B + D) / A);
}
//プラスの最小値を返す(両方マイナスなら0)
public float PlusMin(float a, float b)
{
if (a < 0 && b < 0) return 0;
if (a < 0) return b;
if (b < 0) return a;
return a < b ? a : b;
}
さて、今回の方法では直線移動していない目標には当たりません。
そこで次は円形予測射撃について説明します。
円形予測射撃
等速で円形移動している赤丸を青丸の位置から射撃するとします。
線形と同じような流れで詳細を順番に説明していきます。
まずはごちゃっとした全体図から計算方法を想像してみてください。
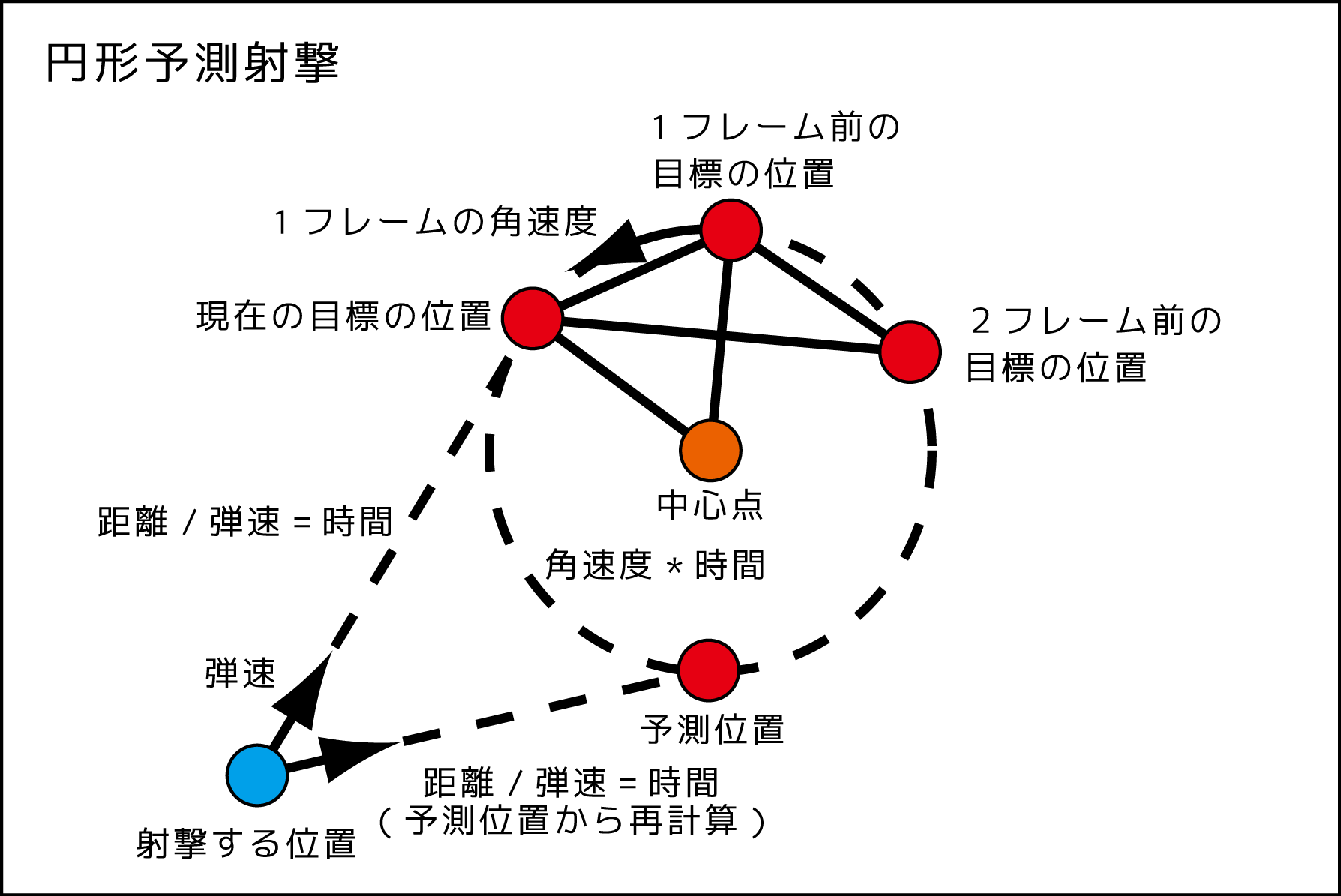
円形予測に必要な情報は5つ
線形予測と比べると「2フレーム前の目標の位置」が必要なので追加します。
- 射撃する位置
- 目標の位置
- 1フレーム前の目標の位置
- 2フレーム前の目標の位置 ← (追加)
- 1フレームに進む弾の速度
※この記事ではFixedUpdateの1フレームを基準とした時間で計算します。

3点の目標位置の角度変化が小さい場合は線形予測に切り替える
今回は目標が円形に進んでいる場合を想定しているので過去2フレームの3点の位置情報から
移動している角度が小さい場合は円形移動していないと判断して線形予測に切り替えます。
計算手順
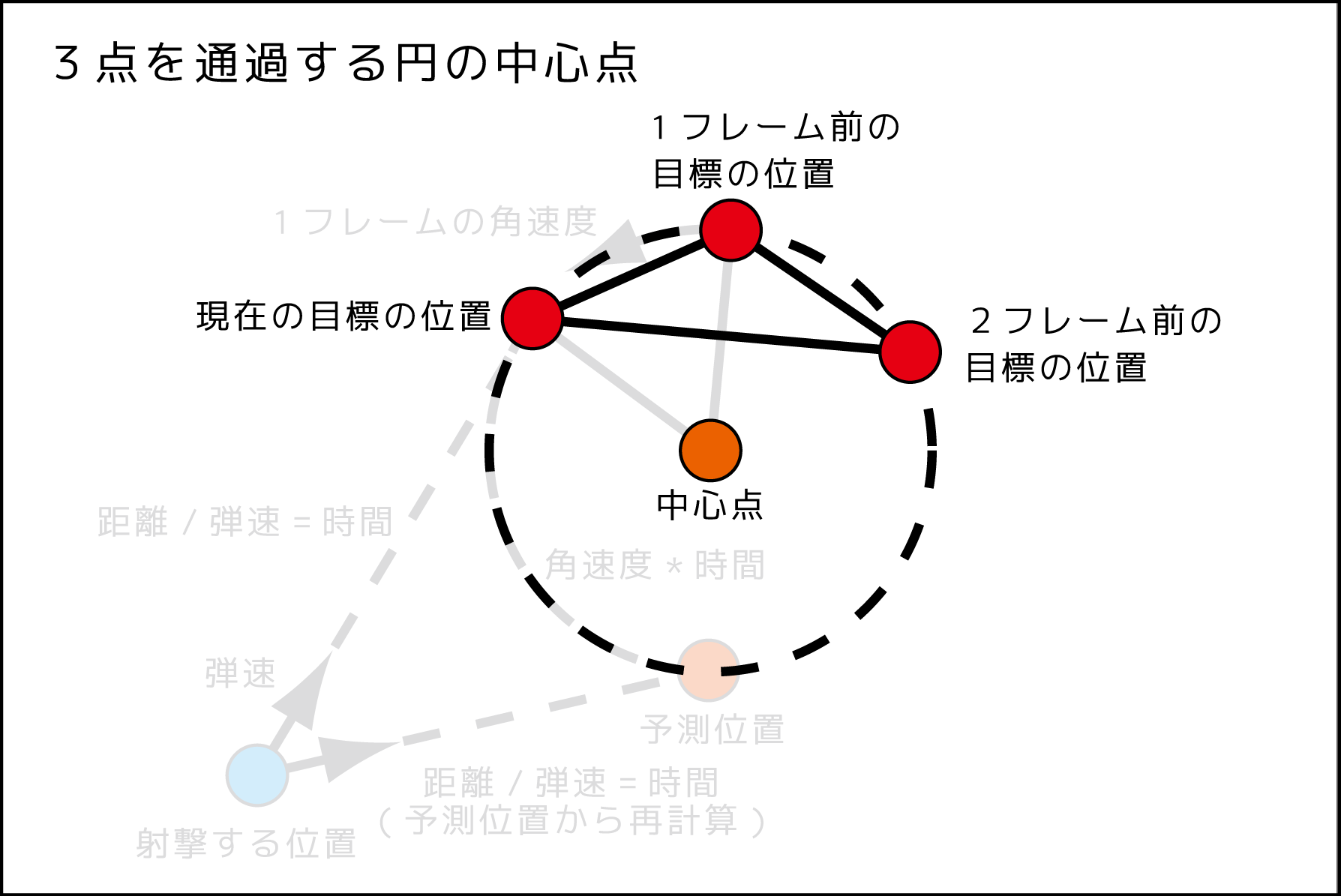
1、3点を通過する円の中心点を計算する
3点を通る円の中心は三角形の外心のことです。
あまり知られてない気がする方法ですが三角形の重心座標系を使って計算します。
三角形の頂点位置をそれぞれ$A、B、C$とし、外心の位置は$P$とします。
$B-C$間の距離の二乗を$edgeA$とします。
$C-A$間の距離の二乗を$edgeB$とします。
$A-B$間の距離の二乗を$edgeC$とします。
$a = edgeA \times (-edgeA + edgeB + edgeC)$
$b = edgeB \times (edgeA - edgeB + edgeC)$
$c = edgeC \times (edgeA + edgeB - edgeC)$
$P=\frac{A \times a + B \times b + C \times c}{a+b+c}$
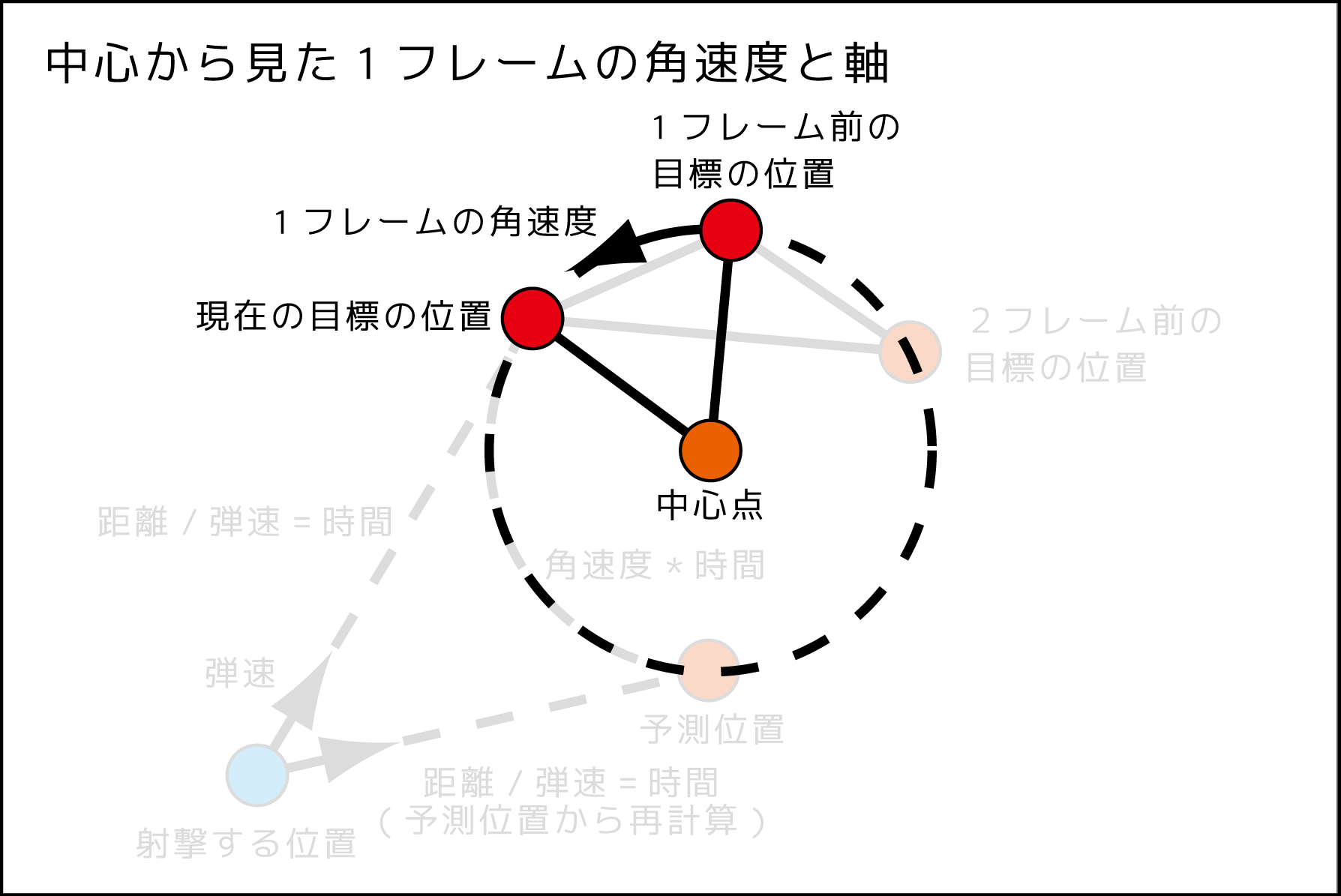
2、中心点から見た1フレームの角速度と回転軸を計算する
回転軸は「中心点から見た1フレーム前の目標位置」と「中心点から見た目標位置」の2つのベクトルの外積を使います。
この図の場合では奥行き方向が回転軸になります。
角速度は1フレームに移動する角度になります。
それぞれUnityにVector3.CrossとVector3.Angleという関数が用意されているので使います
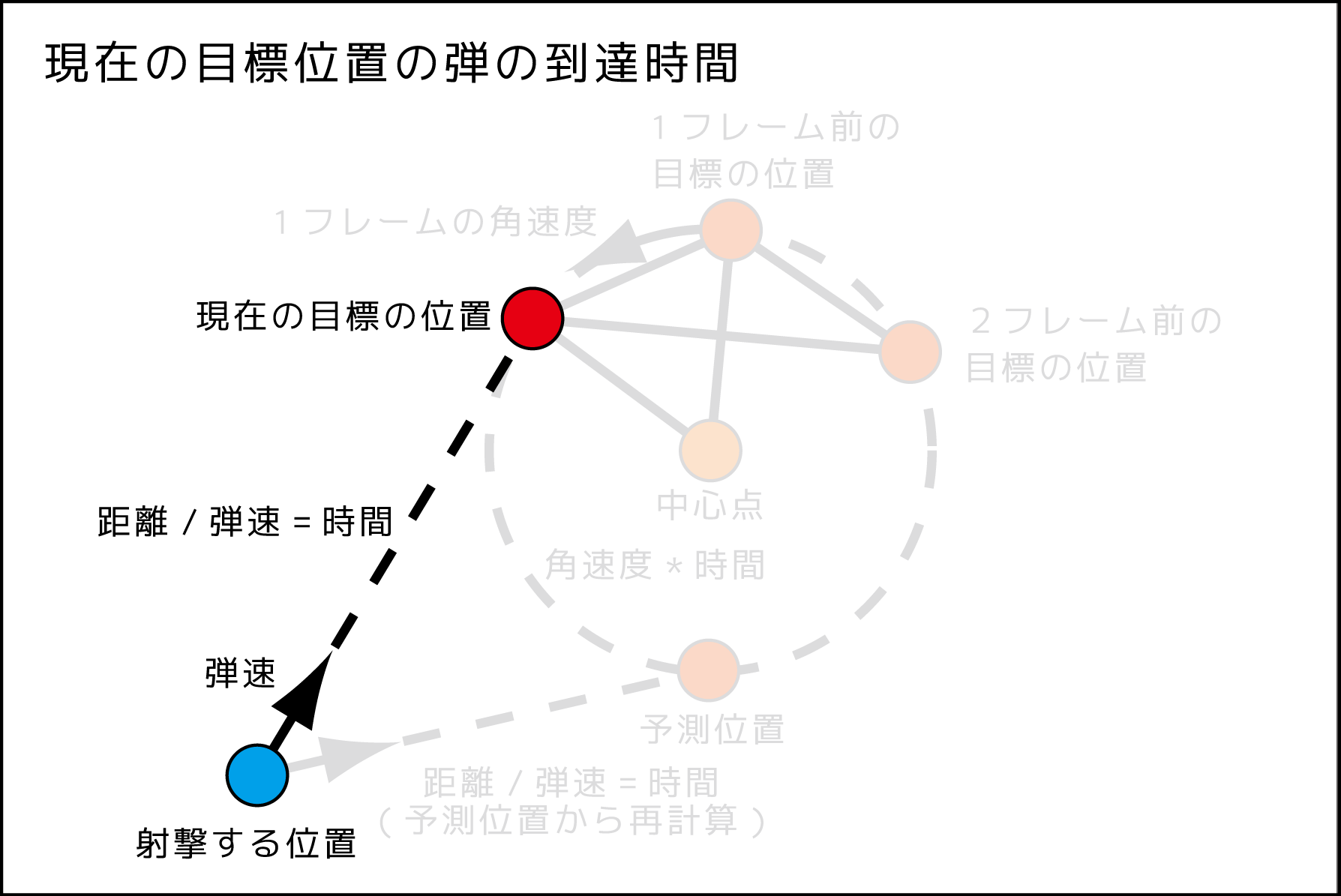
3、現在の目標位置で弾の到達時間を計算する
現在位置までの到達時間は「距離 / 弾速」で時間を仮計算します。
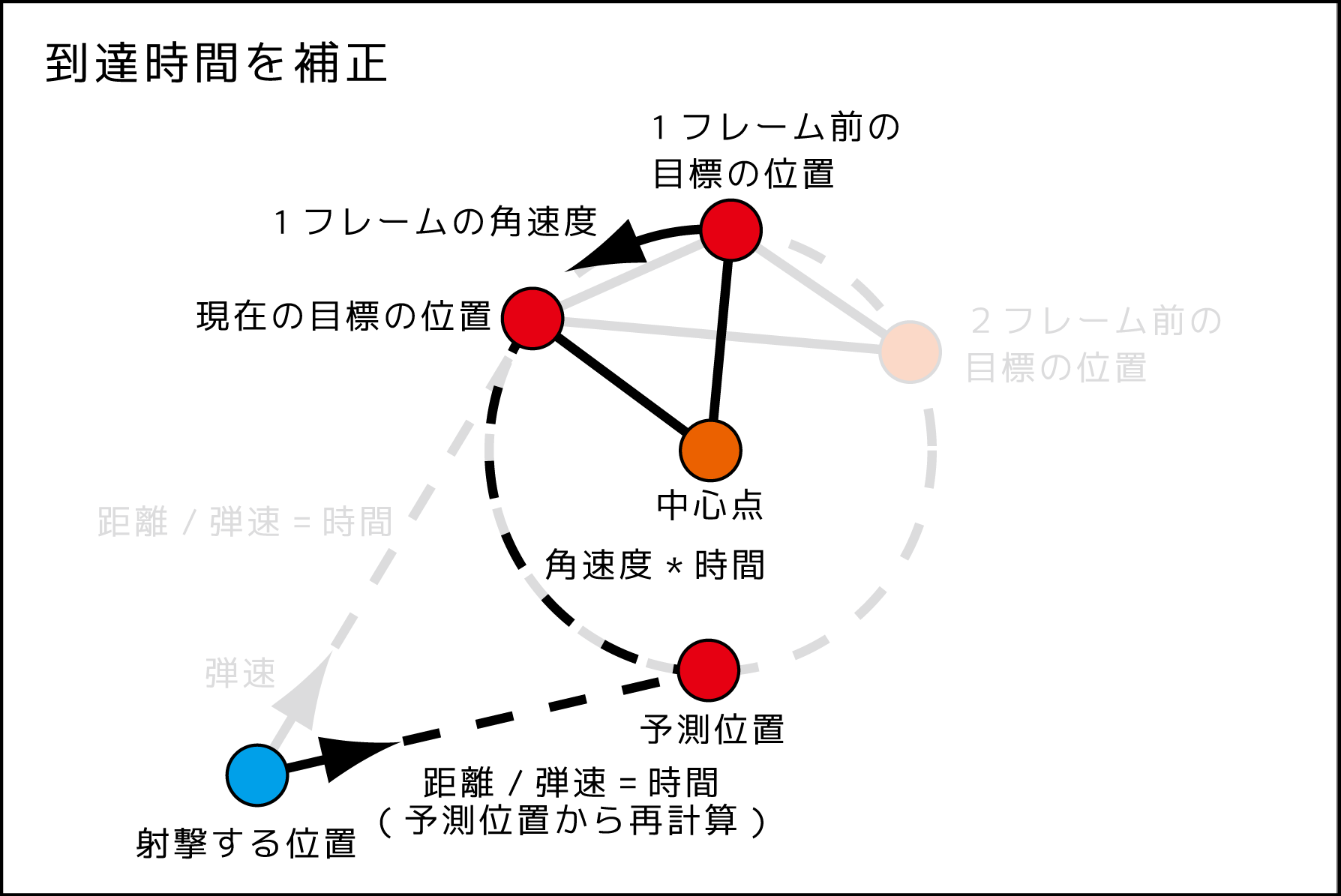
4、到達時間分を移動した予測位置で再計算して到達時間を補正する
弾が到達するころに目標は移動しているので仮計算した時間から位置を計算して
再び弾の到達時間を再計算するという過程を数回繰り返して時間を補正します。
※弾速が遅い場合は到達するまでに円を何回転もして精度が上がらないことがあります。
5、到達時間から弾を撃つべき位置を決定する
得られた時間の値で「$現在位置 + 角速度 \times 時間$」から最終的な予測位置を計算します。
円形予測射撃のスクリプト
// 円形予測射撃のスクリプト
public Vector3 CirclePrediction(Vector3 shotPosition, Vector3 targetPosition, Vector3 targetPrePosition, Vector3 targetPrePosition2, float bulletSpeed)
{
//3点の角度変化が小さい場合は線形予測に切り替え
if (Mathf.Abs(Vector3.Angle(targetPosition- targetPrePosition, targetPrePosition - targetPrePosition2)) < 0.03)
{
return LinePrediction(shotPosition, targetPosition, targetPrePosition, bulletSpeed);
}
//Unityの物理はm/sなのでm/flameにする
bulletSpeed = bulletSpeed * Time.fixedDeltaTime;
//1、3点から円の中心点を出す
Vector3 CenterPosition = Circumcenter(targetPosition, targetPrePosition, targetPrePosition2);
//2、中心点から見た1フレームの角速度と軸を出す
Vector3 axis =Vector3.Cross(targetPrePosition - CenterPosition, targetPosition - CenterPosition);
float angle = Vector3.Angle(targetPrePosition - CenterPosition, targetPosition - CenterPosition);
//3、現在位置で弾の到達時間を出す
float PredictionFlame = Vector3.Distance(targetPosition, shotPosition)/bulletSpeed;
//4、到達時間分を移動した予測位置で再計算して到達時間を補正する。
for (int i = 0; i < 3; ++i)
{
PredictionFlame = Vector3.Distance(RotateToPosition(targetPosition, CenterPosition, axis, angle * PredictionFlame), shotPosition) / bulletSpeed;
}
return RotateToPosition(targetPosition, CenterPosition, axis, angle * PredictionFlame);
}
//三角形の頂点三点の位置から外心の位置を返す
public Vector3 Circumcenter(Vector3 posA, Vector3 posB, Vector3 posC)
{
//三辺の長さの二乗を出す
float edgeA = Vector3.SqrMagnitude(posB - posC);
float edgeB = Vector3.SqrMagnitude(posC - posA);
float edgeC = Vector3.SqrMagnitude(posA - posB);
//重心座標系で計算する
float a = edgeA * (-edgeA + edgeB + edgeC);
float b = edgeB * (edgeA - edgeB + edgeC);
float c = edgeC * (edgeA + edgeB - edgeC);
if (a + b + c == 0) return (posA + posB + posC)/3;//0割り禁止
return (posA * a + posB * b + posC * c) / (a + b + c);
}
//目標位置をセンター位置で軸と角度で回転させた位置を返す
public Vector3 RotateToPosition(Vector3 v3_target, Vector3 v3_center,Vector3 v3_axis, float f_angle)
{
return Quaternion.AngleAxis(f_angle, v3_axis) * (v3_target - v3_center) + v3_center;
}
射撃する側のスクリプト例
using UnityEngine;
public class Shooter : MonoBehaviour {
public GameObject target;//ターゲット
public float bulletSpeed=20;//弾のスピード
public GameObject bulletPrefab;//弾のプレハブ
Vector3 targetPrePosition;
Vector3 targetPrePosition2;
int timer=0;
void FixedUpdate ()
{
Vector3 targetPosition = CirclePrediction(transform.position, target.transform.position, targetPrePosition, targetPrePosition2, bulletSpeed);
targetPrePosition2 = targetPrePosition;
targetPrePosition = target.transform.position;
++timer;
if (timer > 10)
{
timer = 0;
GameObject go = Instantiate(bulletPrefab,transform.position,transform.rotation);
go.GetComponent<Rigidbody>().AddForce((targetPosition - transform.position).normalized*bulletSpeed,ForceMode.VelocityChange);
}
}
}
実装する際の注意点
- FixedUpdateの1フレームを基準とした時間で計算しています。
- 弾速が遅い場合は予測の計算ができない場合があります。
- 弾に対する重力や空気抵抗の影響は考慮していません。
- 計算した時のフレームに弾を発射する場合を想定しています。
- 弾が当たるようになってもゲームが面白くなるかはわかりません。
最後に
記事を書きながら改めて数学はすばらしい道具でもっと使いこなせるようになりたいと思いました。
この記事から何か得るものがあればうれしいです。
最後まで読んでいただきありがとうございました。
未来を予測してより良いクリスマスを迎えましょう!!