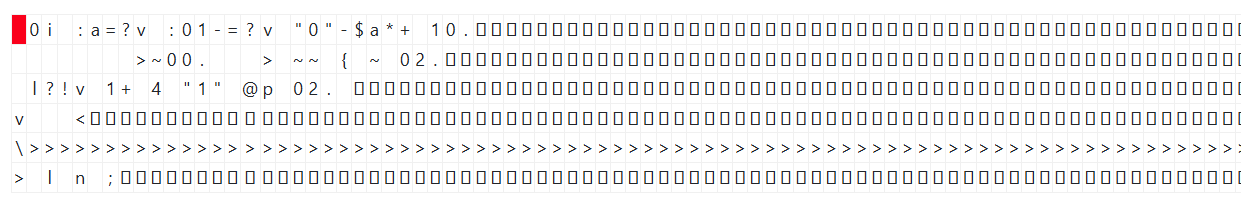前回の記事を読まれていない方は,先に前回を読むことを推奨します.
① ><>とは何か編
② Practice~第3問編
次回はこちらです.
④ 完結編
はじめに
こんにちは,><>で AtCoder Beginning Section を解いていく記事その3です.
今回は AtCoder Beginning Section の第4問 Coins ~ 第7問 Kagami Mochi までの解説を行います.
前回は難易度順に解いていきましたが今回は順番通り解いていきます.なぜならどの問題も><>にとって難しい問題だからです...
第4問 ABC087B Coins
A (LF) B (LF) C (LF) X (LF)が与えられるので,$500a+100b+50c = X$を満たす$a,b,c$の組み合わせの数を出力する問題です.(ただし,$0 \leq a \leq A$,$0 \leq b \leq B$,$0 \leq c \leq C$です)
$0 \leq A,B,C \leq 50$程度なので単なる全探索で問題ありませんが,><>でC言語のようなforループを再現するのは大変です.
int res = 0;
for(int a = 0; a <= A; ++a){
for(int b = 0; b <= B; ++b){
for(int c = 0; c <= C; ++c){
if (500 * a + 100 * b + 50 * c == X) {
++res;
}
}
}
}
cout << res << endl;
大変ですが,他にいい方法が思いつかないので(2024/10/27現在,AtCoderProgramで確認した限り,第4問~第10問を><>で提出しているのは私だけです),for文を><>で再現してみました.
まずいつものコードで入力を受けとったのち,p命令で$A,B,C,X$の値をコード上に書き込みます.以降は値が必要になったら,g命令で受け取るようにします.
そしてスタックには$a,b,c$を追加し,値をインクリメントしながら$A,B,C$の値を超えたらリセットしてループを回します.すべての値が最大まで大きくなったらループを抜け結果を出力します.
それぞれの変数の書き込み位置は$A(0,1)$,$B(1,1)$,$C(2,1)$,$X(3,1)$です.また結果も$(4,1)$に書き込んでいます.わかりやすくするために,コードに書き込み位置を大文字で書き込んでおります.
0i :01-=?v :a=?v "0"-$a*+ 10.
ABCXR >~~ 02. > ~ 00.
r 01p 11p 21p 31p 0 41p 03.
0 0 0 04.
: 5a* * } > $ : aa* * } $ > @@ : 5aa** * } @ > {{{++ 05.
31g =?v > 07.
> 41g 1+ 41p ^
{ 1+ : 01g 1+ =?!v ~0 } 09.
> } 04.
$ 1+ : 11g 1+ =?!v ~0 $ 0b.
> $ 04.
1+ : 21g 1+ =?!v 41g n ;
> 04.
最長実行時間 : 508ms
提出したコードはこちら.
なお,実行時間を見て頂ければわかる通り,p命令は非常に遅いです.濫用に注意しないとすぐTLEします.今回は最大でも$50^3=125000 \approx 10^5$程度なので問題ありません.
また,折角スタック指向言語の><>を使っているのに,普通のプログラミング言語のような実装をしてしまっているのは美しくないですが,ACがとれるのでよしとしました.
以下に各行の処理を説明します.
1行目と2行目は入力を受け取る処理です.スタックには$A,B,C,X$があります.受け取り終わったら3行目にジャンプします.また,2行目の先頭に,$A,B,C,X$の値と答えを書き込みます.
3行目は2行目に$A,B,C,X$の値と答えの初期値(0)を書き込む処理です.この時点でスタックは空になります.終了したら4行目にジャンプします.
4行目はスタックに0を3つ追加しています.これがforのa b cです.終了したら,5行目にジャンプします.
5行目から,7行目までが,$500a+100b+50c = X$を確認する処理です.5行目はa b cの並び順を変化させずに$500a+100b+50c$を計算しています.項ごとに>を挿入しているので,読むときは参考にしてください.
6行目,7行目で$X$の値を取り出して,等しければ答えをインクリメントします.終了後8行目にジャンプします.
8行目以降はfor文の処理です.2行ごとにa b cの処理となっています.それぞれ値をインクリメントした後,5行目に戻ります.最終行のみ,これ以上値がインクリメントできなければ,結果をnして終了します.
第5問 ABC083B - Some Sums
N (SPC) A (SPC) B (LF)が与えられるので,1以上$N$以下の整数のうち,各桁の和がA以上B以下であるものの総和を出力する問題です.
この問題も$1 \leq n \leq N$となる n を,for文の要領でインクリメントして計算するだけです.変数の量が少なくなる分先ほどよりも簡単です.
int res = 0;
for(int n = 1; n <= N; ++n) {
int n_copy = n;
int a = n_copy % 10;
n_copy = n_copy / 10;
int b = n_copy % 10;
n_copy = n_copy / 10;
int c = n_copy % 10;
n_copy = n_copy / 10;
int d = n_copy % 10;
n_copy = n_copy / 10;
int sum = a + b + c + d + n_copy;
if (sum < A || B < sum) continue;
res += n;
}
cout << res << endl;
唯一の問題は上記のn_copy = n_copy / 10;の処理です.><>の割り算はfloat型で答えが返ってきます.例えば,$12 \div 10 = 1.2$です.
これは今回の問題的には大変不都合です.そこで先に余りを求め引いておくことで,intの割り算を再現しています.$(12 - 12 mod 10) \div 10 = 1$
0i :01-=?v :" "=?v :a=?v "0"-$a*+ 10.
NABR > ~~ 02.> >~00.
21p 11p 01p 0 31p 1 03.
: : a% :}- a, : a% :}- a, : a% :}- a, : a% :}- a, {{{{++++ 04.
: 11g ( ?v : 21g ) ?v ~: 31g+ 31p > 1+ : 01g )?v 03.
> > ~ ^ > 31g n;
最長実行時間 : 52ms
提出したコードはこちら
やっていることはだいたい第4問と一緒なので解説は省略します.
第6問 ABC088B - Card Game for Two
N (LF) A1 (SPC) A2 (SPC) ... (SPC) ANが与えられるので,Aを降順にソートして上から足す,引く,足す...を繰り返した結果を出力せよという問題です.
少なくとも入力の受け取りと,足す,引く,足す...の処理は簡単に実装出来そうですが,問題はソートです.今回は$N$の最大値が$100$であることを生かしてバブルソートでソートしていこうと思います.バブルソートとは数列を順にみていき,順番が逆であれば入れ替える処理を繰り返していくだけのシンプルなアルゴリズムです.ワーストケースでは$O(N^2)$となりますが,今回ならば$10^4$程度なので問題ありません.
バブルソートでは1回目の入れ替えで1つの数字が確定,2回目で2つの数字が確定...と繰り返すごとに数字が確定していくので,比較回数が減っていきます.しかし,これを実装するとかえって面倒なので,愚直に$(N-1)$回比較するのを$(N-1)$回繰り返します.
0i :01-=?v :" "=?v :a=?v "0"-$a*+ 10.
NijR > ~~ 02.> >~00.
{ 01p 0 11p 0 21p 0 31p 03.
:&$:@& )?!$ } 11g 01g 2- =?v 11g1+ 11p
> } 0 11p 21g 01g 2- =?v 21g1+ 21p 03.
> r 06.
l?!v 31g+ 31p l?!v 31g $ - 31p 06.
> > 31g n;
最長実行時間 : 24ms
提出したコードはこちら
もはやほとんどいままでの問題の繰り返しです.そのため,簡単に説明します.
3行目では,比較回数のカウンタをi,繰り返しのカウンタをjとしてそれぞれ$(1,1)$と$(2,1)$に書き込んでいます.再確認いたしますが,コード上にもi jと書いてあるのは,分かりやすくするためでとくに意味はありません.
4~6行目がバブルソートのプログラムです.
重要なのは4行目の初めの :&$:@& でしょうか.これは XX...XXAB のようなスタックの最後の要素2つを順番を変えずに複製することができる(XX...XXABAB)プログラムです.レジスタが空でなければ使用できませんが,比較的シンプルにかけるので覚えておきましょう.><>の比較演算子はスタックから値を取り出して比較するので,スタックに値を残しておきたい場合,このようにする必要があります.
$(N-1)$回ループしますが,i j は0-indexなので,$N-2$と比較しています.
7,8行目は結果の出力です.l?!vはスタックが空であれば下に行くプログラムです.?は0か0以外かで判断するので,=を省略できます.
第7問 ABC085B - Kagami Mochi
今回解説する最後の問題です.N (LF) A1 (LF) A2 (LF) ... (LF) ANが入力されるので,Aの種類を出力する問題です.
C++であればAの値をsetにいれてsize()するだけの問題ですね.><>ではどのように解きましょうか?2つほど方針があるかと思います.
- Aをソートして要素を確認し,重複する値を削除してからスタックの大きさ
lをnする - $Ai$($0 \leq i \leq N$)について,$r$行$Ai$列に対して,適当な数値を書き込んでいき,$r$行目を$(r,0)$から$(r,100)$まで移動してから,スタックの大きさ
lをnする
今回は$N$の値が小さいのでどちらでも問題なさそうです.(ちなみに$N$の値が大きい場合,どちらも使えません...)
せっかくなので今回はソートを使わないほうを実装してみます.><>でsetを再現するため.コードボックスの座標をkeyに見立てて値を書き込んでいきます.
0i :a=?v :01-=?v "0"-$a*+ 10.
>~00. > ~~ { ~ 02.
l?!v 1+ 4 "1" @p 02.
v <
\>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>
> l n ;
最長実行時間 : 1ms
提出したコードはこちら
とてつもなく横長なコードですね.これはAtCoderの><>のインタープリタはコードボックスの外にpで書き込んだ命令を実行できない(公式のインタープリタはできます,C++でいうところのg++とMSVCの違いみたいなものです)仕様のためで,あらかじめ>で書き込む領域を埋め尽くしています.
結びに
次回で最終回となります.
AtCoder Beginning Section の問題を解き終わった後は,><>の高速化テクニックを紹介したいと思います.
今回解説したコードはこちら
- ABC087B - Coins https://atcoder.jp/contests/abs/submissions/59259112
- ABC083B - Some Sums https://atcoder.jp/contests/abs/submissions/59259340
- ABC088B - Card Game for Two https://atcoder.jp/contests/abs/submissions/59260200
- ABC085B - Kagami Mochi https://atcoder.jp/contests/abs/submissions/59260741
第8問以降のコードはこちら
- ABC085C - Otoshidama https://atcoder.jp/contests/abs/submissions/59128526
- ABC049C - 白昼夢 https://atcoder.jp/contests/abs/submissions/59094580
- ABC086C - Traveling https://atcoder.jp/contests/abs/submissions/59130970