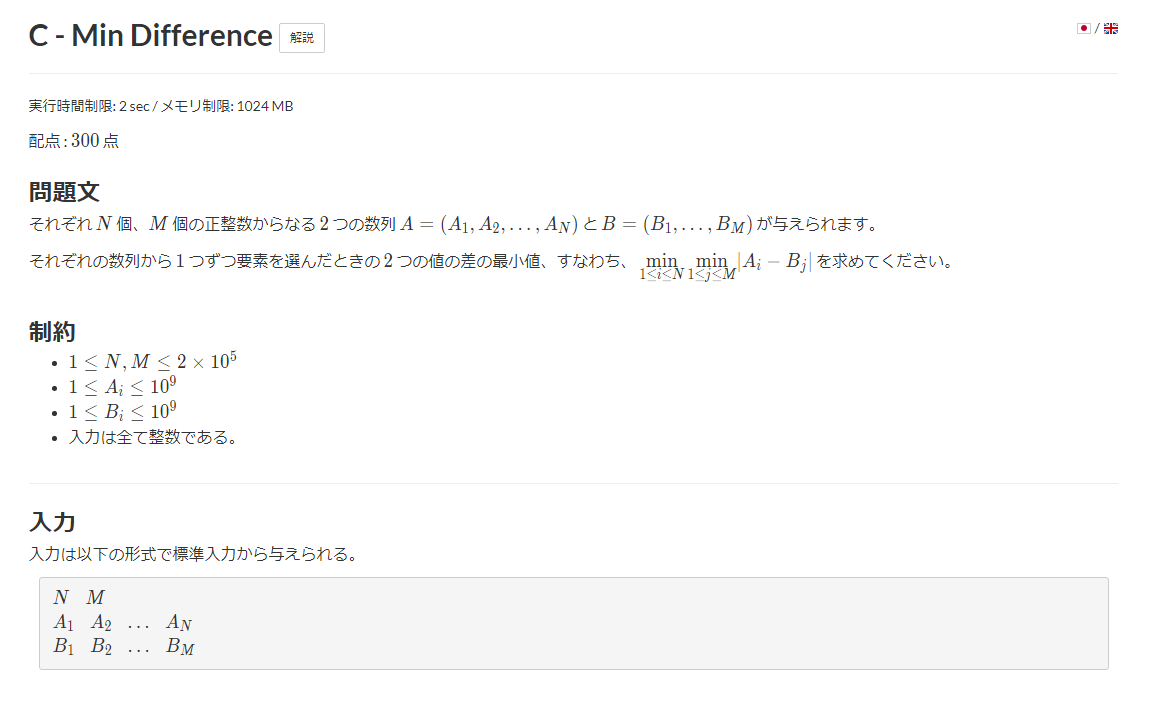
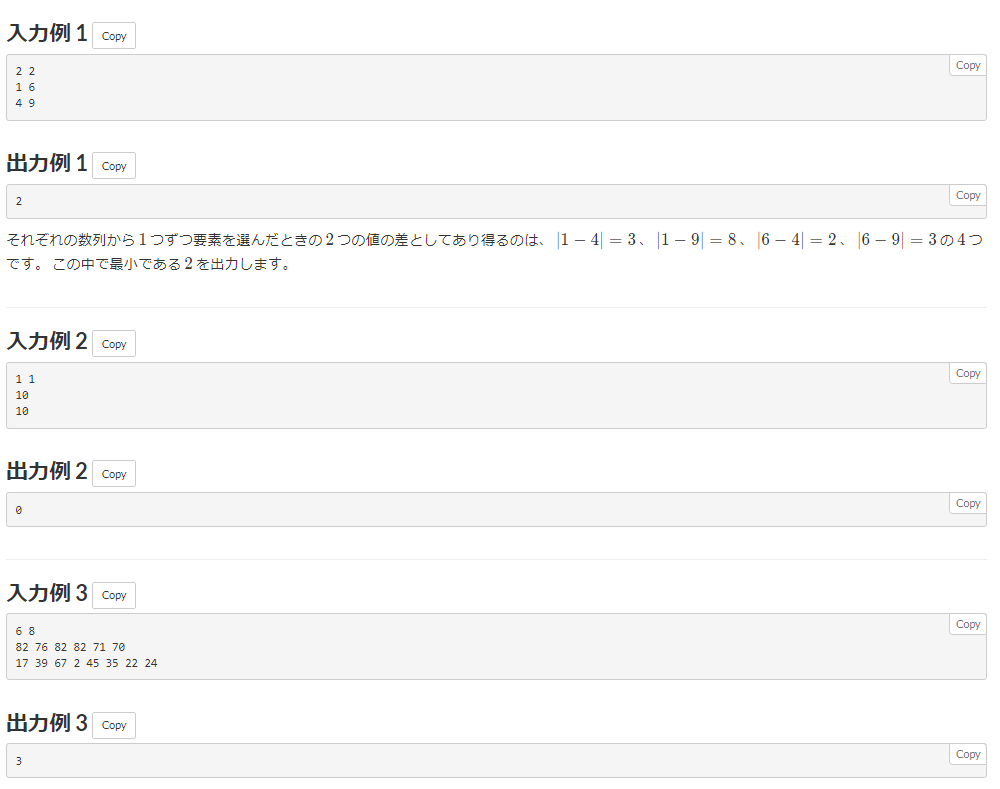
2重 for で全探索してもよいが、計算量が 4*10^10 となり、TLE となる。
糸口を探すため、とりあえずサンプルを確認してみる。
個人的に注目したのは入力例3。
最小値を探すってことは、数列 A , 数列 B の中から値が近い要素の組み合わせを出せば良いんだよね？
ココから更に飛躍が入ります。
じゃあ、数列 A と数列 B を合体して sort したら A[n]=>B[m] or B[m]=>A[n] となる並びが必ずあり、
その中から差分が最小となる組み合わせを探せば良いんだよね？
っと言うことで、これで行けました。
MinDifference_1.py
N,M = map(int,input().split())
A = list(map(int,input().split()))
B = list(map(int,input().split()))
A = list(set(A))#A の重複要素を排除
B = list(set(B))#B の重複要素を排除
#A,B を合体すると、ごちゃまぜで分からなくなるので、
#辞書で管理することにしました。
dicA = {}
dicB = {}
for i in range(len(A)):
dicA[A[i]] = 1#冒頭で set() してるので重複要素なし、要素は必ず 1 つ
for i in range(len(B)):
dicB[B[i]] = 1#冒頭で set() してるので重複要素なし、要素は必ず 1 つ
X = A + B # AとB を合体
X.sort() # sort する
ans = float("inf") # 無限大より小さいものを for で探す
#辞書はリストに無い key の所在を尋ねると Error を返します。
#if X[i] in dicA としても良かったかもだが、dicA/dicB の要素数が計算量として上乗せされる。
#そのため 2*10^5 x 2*10^5 となる可能性があるので記述は避けた。
#代わりに try / except を使って計算量を抑えた.
for i in range(len(X)-1):#=> X を端から確認し、X[i],X[i+1] の差分をcheck。
try:
if dicA[X[i]] == 1 and dicB[X[i+1]] == 1:#辞書で X[i],X[i+1] がそれぞれ A,B であることを確認
if abs(X[i]-X[i+1]) < ans:
ans = abs(X[i]-X[i+1])
except:#上記で Error で返したら、以下の処理に入る
try:
if dicB[X[i]]==1 and dicA[X[i+1]]==1:#辞書で X[i],X[i+1] がそれぞれ A,B であることを確認
if abs(X[i] - X[i + 1]) < ans:
ans = abs(X[i] - X[i + 1])
except:
pass#上記でもダメなら pass。次の検証に向かう
print(ans)
きっと、もっと分かり易くて良い解法があるはず。
とりあえず、ほかの人の解法も読みながらイメージを積み上げてみようと思う。
感動したら、追記するかも。
理解があやふやかもしれないが、
上記の場合の計算量は O(N) だと思うが相違ないだろうか？
有識者のアドバイスがあれば助かります m(_ _)m
あれから
まだまだ少ないが色々解いて見識が広がったと信じ、再チャレンジ。
以下でも通った。
MinDifference_2.py
N,M = map(int,input().split())
A = list(map(int,input().split()))
B = list(map(int,input().split()))
dicA = {}
dicB = {}
for n in range(N):
if A[n] not in dicA:
dicA[A[n]] = 0
dicA[A[n]] += 1
for m in range(M):
if B[m] not in dicB:
dicB[B[m]] = 0
dicB[B[m]] += 1
X = A + B
X.sort()
score = float("inf")
for i in range(N+M-1):#max O(4*10**5)
if X[i] in dicA and X[i+1] in dicB or X[i] in dicB and X[i+1] in dicA:
score = min(score,abs(X[i]-X[i+1]))
print(score)
改善点
・A/B の重複削除の記述を排除
仮に重複があったともして前述にあるように O(4*10^5) なので計算量は問題にならないし、答えが変わることはない。
・try/except の記述を削除
辞書の in演算は O(1) なのでガンガン使うことで記述が計算量を気にせず、シンプルに書ける。