こんばんは!(^^)!
昨日は、子供を寝かしつけようとして
そのまま自分も寝てしまいました(笑)。
では、クイックソートで小さい順に並べ替えてみましょう。
これまた面白い考え方でした。
今回は while を使います。復習を兼ねて簡単な奴を書いてみました。
x = 10
pc = 5
# x > pc だったら、while の中に入って処理を実行
# !(x > pc) となったら、while 文は pass !
while x > pc:
x -= 1
print(x)
print("result is ",x)
ご覧の通り、x > pc である限り、while 文の中をグルグル回るのですが、
そのたびに x = x - 1 が実行されます。
その後、x = 6 になったら、一応 while 文の中に入れますが、
中の処理で x -= 1 となるので、x = 5 になるために、x > pc の関係が崩れるので、
次の処理では while 文を抜けざるを得ません。。
念のため、実行結果を載せます。
9
8
7
6
5
result is 5
以上から while 文のミソは、条件文に該当する限り、
処理を繰り返すことが出来る点です。
なんで、こんなの使うの?って話ですよね。
じゃあ、本題に入っていきましょう
(後で while が出てくるので覚えておいてください)。
今回はこちらの配列Xを使います。

この配列の中央の値が何であっても、こいつを基準にソートをしていきたいと思います。
???何と比較するの???
はい、すいません。
一番左の値と、中央値を比較します。

一応、1 vs. 5 明らかに中央値である 5 の方が大きいですね。
じゃあ、次です。

8 vs. 5 ! これは明らかに 8 の方が大きいですよね。
はい Stop !!。
First step の中央値より大きい値を見つける作業はここで終了です。
Second step は右端から中央値より小さいを見つける作業を行います。
じゃあ、端から行きましょう。

5 vs. 9 !
Stay で大丈夫ですね。次です!

5 vs. 3 !
中央値の方が大きいですね。
OK です。見つけました。
Step 2 終了です。
次のステップは Step 1 と Step2 それぞれで見つけた値をひっくり返します。
※Step 1: 中央値より大きい値を見つける
※Step 2: 中央値より小さい値を見つける
イメージはこちらです。
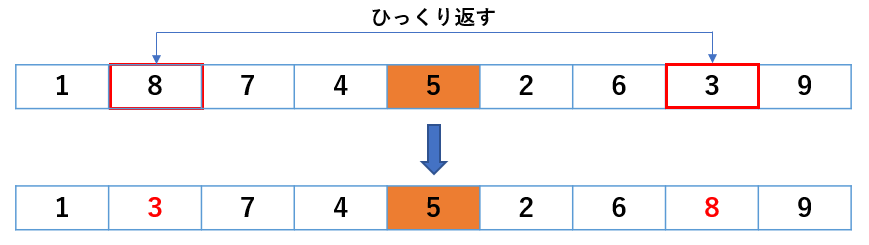
変更後を赤字にしましたが、どうでしょうか?
それっぽく並び替え出来てますよね、大事です、雰囲気(笑)
では次に何をするのか?
Step 1,Step 2 を繰り返します。但し、Lptr +=1,Rptr -=1 とします。
そう、中央値に近づくようにして、同じことを繰り返していきます。
????なんで?
まぁ、まぁ、やってみましょうよ。
具体的には X[2] vs X[4] と X[4] vs X[6] です。
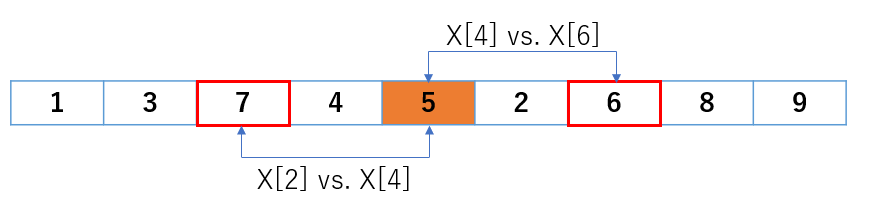
X[2] vs X[4] はビンゴですが、X[4] vs X[6] の場合は、
X[4] < X[6] が成り立っているので、次の X[4] vs X[5] を実行します。
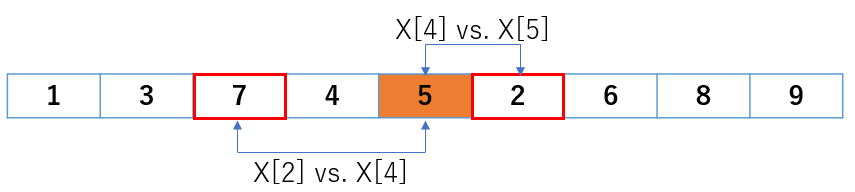
さぁ、交換の御時間です(笑)
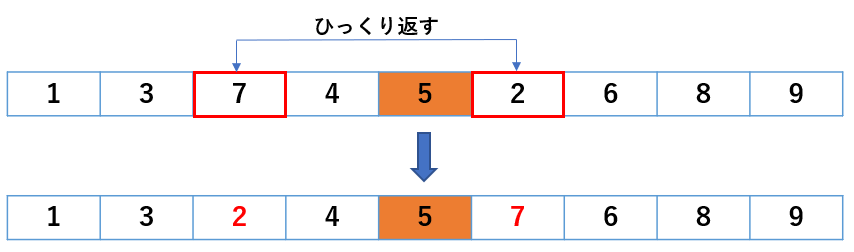
以上で中央値 5 より左側の値は全て 5 未満、
中央値より右側は 5 より大きい配列が完成しました。
ここまでの動きをコードに落としてみましょう。
例えばですが、左側から中央値によって行く値を x[Lptr],
右側から中央値によって行く引数を x[Rptr] としてはどうでしょう。
※Lptr = Left pointer / Rptr = Right pointerセンス皆無(笑)!?
# 配列
x = [1,8,7,4,5,2,6,3,9]
# 中央のポインタ
cen = len(x)//2
Lptr = 0
Rptr = len(x)-1
# x[Lptr] は中央値より小さい限り、ポインタ Lptr はインクリメント
while x[Lptr] < x[cen]:
Lptr += 1
# x[Rptr] は中央値より大きい限り、ポインタ Rptr はディクリメント
while x[cen] < x[Rptr]:
Rptr -= 1
# 念のため、Lptr < Rptr であることをトリガにしておく
if Lptr < Rptr:
#値をひっくり返す
x[Lptr],x[Rptr] = x[Rptr],x[Lptr]
実行してみましょう。
# 実行前
# [1,8,7,4,5,2,6,3,9]
# 実行後
[1,3,7,4,5,2,6,8,9]
あれ? 3 と 8 がひっくり返っただけですね(笑)
そうか。
中央値より大きい/小さい値を探して
ひっくり返す作業を 1 回しか上記では表現出来ていませんね。
上記の記述を while Lptr < Rptr とすれば、この関係を維持する限り
前述の記述を繰り返してくれます(思い出して! 冒頭の while の説明!!)。
x = [1,8,7,4,5,2,6,3,9]
cen = len(x)//2
Lptr = 0
Rptr = len(x)-1
# ポインタの位置 Lptr < Rptr の関係を維持している限り
# while 分の中身の処理を続けます。
while Lptr < Rptr:
while x[Lptr] < x[cen]:Lptr += 1
while x[cen] < x[Rptr]:Rptr -= 1
if Lptr < Rptr:
x[Lptr],x[Rptr] = x[Rptr],x[Lptr]
#ひっくり返す作業が終了したら以下の作業をして
#次の比較作業に入れるようにします。
Lptr += 1
Rptr -= 1
print(x)
実行結果は以下になります。
# 実行前
# [1,8,7,4,5,2,6,3,9]
[1,3,2,4,5,7,6,8,9]
うん!(^^)!
中央値の 5 より左側は 5 未満
中央値の 5 より右側は 5 より大きい値に出来た( *´艸`)
っで、どうします?次(笑)
まずは、前述の処理を行った後に
Lptr,Rptr は何処に辿り着いたんでしょうか。
while Lptr < Rptr:
while x[Lptr] < x[cen]:Lptr += 1
while x[cen] < x[Rptr]:Rptr -= 1
Lptr = 3 の時に Lptr += 1 なので、Lptr = 4
Rptr = 5 の時に Rptr -= 1 なので、Rptr = 4
Lptr = Rptr = 4 となり、while 文の条件であった Lptr < Rptr が
これで崩れますので、while 文を抜けます。
念のため、実行してみましょう。
[1, 3, 2, 4, 5, 7, 6, 8, 9] Lptr = 4 Rptr = 4
なるほど。とりあえず、図にしてみましょう。
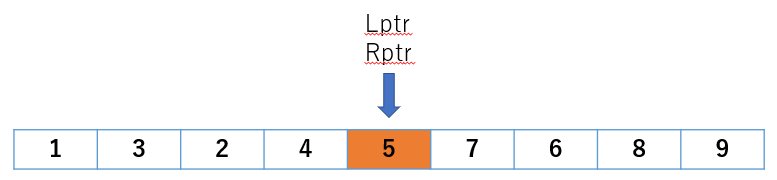
以下のように追加で少しイジルとどうでしょうか。
x = [1,8,7,4,5,2,6,3,9]
cen = len(x)//2
Lptr = 0
Rptr = len(x)-1
#↓ "=" を追加!!
while Lptr <= Rptr: # Lptr == Rptr でも while 内の処理に入る
#以下の while はスキップします。
#<===ここから
while x[Lptr] < x[cen]:Lptr += 1
while x[cen] < x[Rptr]:Rptr -= 1
#<== ここまで
# Lptr == Rptr でも while 内の処理に入る
#↓ "=" を追加!!
if Lptr <= Rptr:
#x[4],x[4] = x[4],x[4] なので無害
x[Lptr],x[Rptr] = x[Rptr],x[Lptr]
#ここが重要!!それぞれインクリメント、ディクリメント!
Lptr += 1
Rptr -= 1
print(x,f"Lptr = {Lptr}",f" Rptr = {Rptr}")
一部に "=" を追加しました。
これにより実行結果は以下のようになります。
[1, 3, 2, 4, 5, 7, 6, 8, 9] Lptr = 5 Rptr = 3
なんと、Lptr と Rptr の位置が逆転しました。
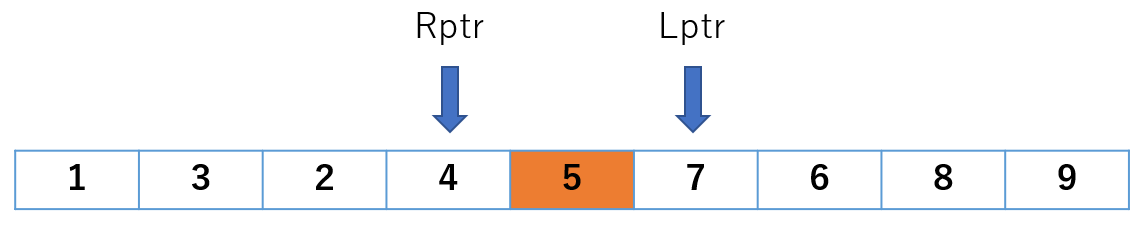
ではでは、この状態で与えられた配列 x を、
領域1: x[0] ~ Rptr(=x[3])
領域2: Lptr(=x[5]) ~ x[8]
っと分けて、それぞれに今までと同じ処理を行ったら、どうなりますか?
そうです、再帰です。
なんか生まれそうですよね!?(笑)
再帰を使いやすくするために記述を変えておきます。
# left :初期値としては一番左
# right:初期値としては一番右
def quick_sort(x,left,right):
Lptr = left
Rptr = right
cen = (left+right)//2
while Lptr <= Rptr:
while x[Lptr] < x[cen]:Lptr += 1
while x[cen] < x[Rptr]:Rptr -= 1
if Lptr <= Rptr:
x[Lptr],x[Rptr] = x[Rptr],x[Lptr]
Lptr += 1
Rptr -= 1
print(x,f"Lptr = {Lptr}",f" Rptr = {Rptr}")
if __name__ =="__main__":
x = [1,8,7,4,5,2,6,3,9]
# 使用する配列 x
# left の初期値は左端なので 0 を入力
# right の初期値は右端なので len(x)-1 を入力
quick_sort(x,0,len(x)-1)
これから再帰のイメージは以下の通りです。
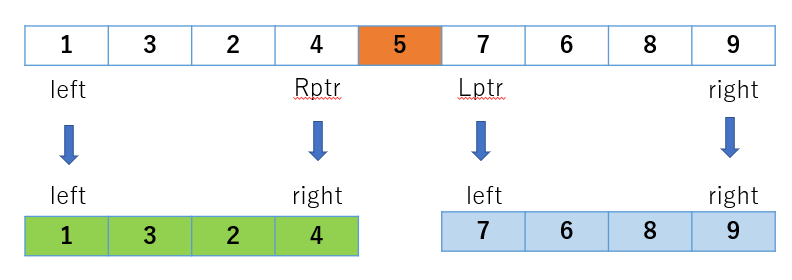
left , Rptr を left , right とした領域(緑)、
Lptr , right を left , right とした領域(青)なんか動きそうですね。
こんな記述は如何でしょうか。
def quick_sort(x,left,right):
Lptr = left
Rptr = right
cen = (left+right)//2
while Lptr <= Rptr:
while x[Lptr] < x[cen]:Lptr += 1
while x[cen] < x[Rptr]:Rptr -= 1
if Lptr <= Rptr:
x[Lptr],x[Rptr] = x[Rptr],x[Lptr]
Lptr += 1
Rptr -= 1
print(x,f"Lptr = {Lptr}",f" Rptr = {Rptr}")
#前述の図にあるように left < Rptr の関係が成り立てば
#左領域を再帰でソート
if left < Rptr:
quick_sort(x,left,Rptr)
#前述の図にあるように Lptr < right の関係が成り立てば
#右領域を再帰でソート
if Lptr < right:
quick_sort(x,Lptr,right)
if __name__ =="__main__":
x = [1,8,7,4,5,2,6,3,9]
quick_sort(x,0,len(x)-1)
実行結果はこちらです。
[1, 3, 2, 4, 5, 7, 6, 8, 9] Lptr = 5 Rptr = 3
[1, 2, 3, 4, 5, 7, 6, 8, 9] Lptr = 2 Rptr = 1
[1, 2, 3, 4, 5, 7, 6, 8, 9] Lptr = 1 Rptr = -1
[1, 2, 3, 4, 5, 7, 6, 8, 9] Lptr = 3 Rptr = 1
[1, 2, 3, 4, 5, 6, 7, 8, 9] Lptr = 6 Rptr = 5
[1, 2, 3, 4, 5, 6, 7, 8, 9] Lptr = 8 Rptr = 6
最後の行を見ると、ソートされていますね。
途中経過の解説はどうしよう、やったほうが良いかな(;´・ω・)
その後
2020/11/05 丸っきり忘れたので、
今更自分の記事を読み返しました。
なるほど、分かり易い(笑)
ただ、書いた本人が今になって、まるっきり忘れているので、
内容が軽いんだと思います(*´з`)
とりあえず、読み直して自分の中にイメージを作りました。
例のごとく、ホワイトボードに向かいましたが、下の図にある { までは何とか。。
①、② のような再帰処理が出来ませんでした。
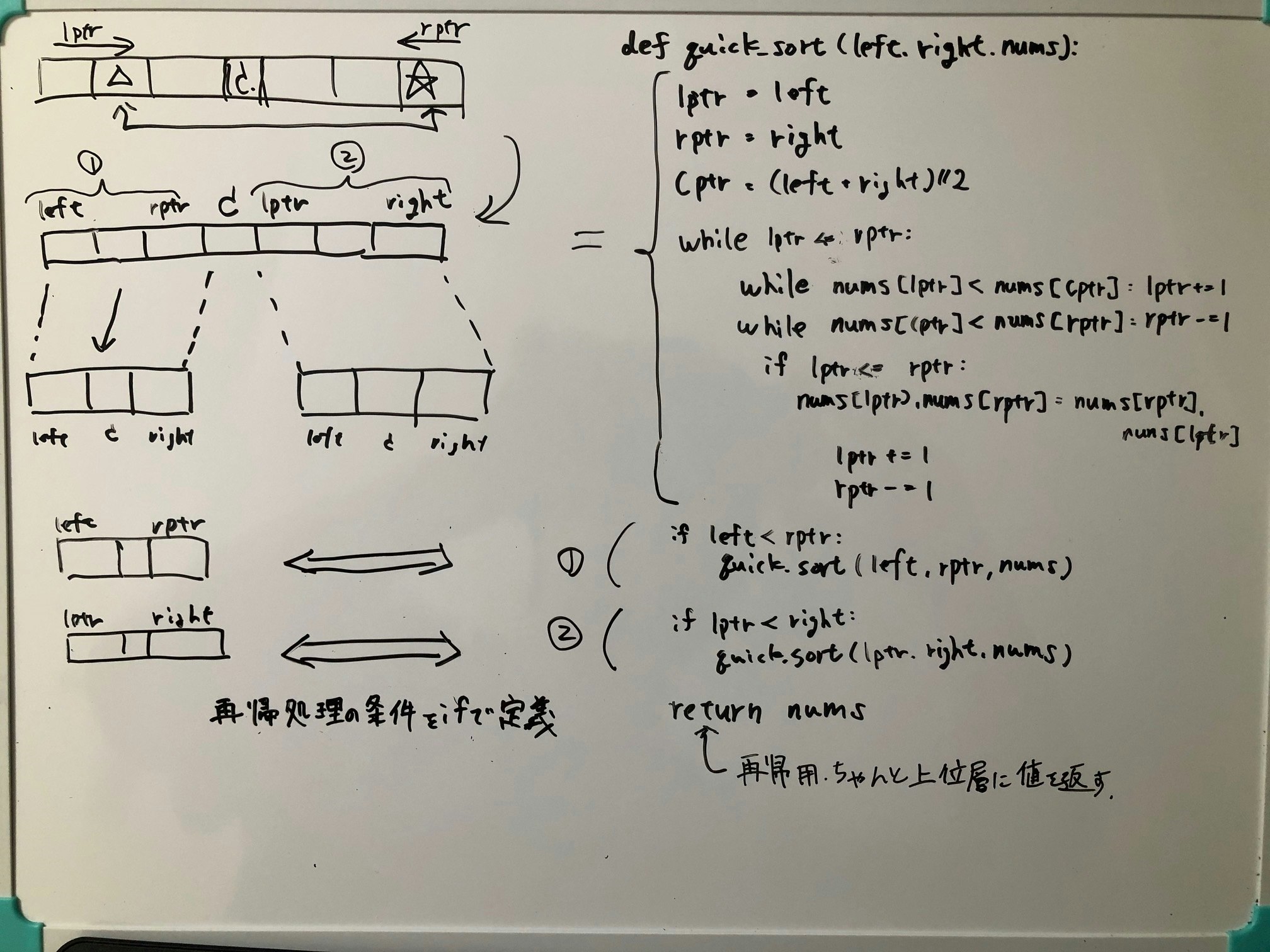
図にも書きましたが、センターを超えた後に分割したい領域の両端が、
left < rptr, lptr < right であることをさえわかれば
if 文で条件を定義してあげることで再帰処理に導けます。
確かに、再帰処理はそんなことしてましたよ(笑)。
あと昔の自分の記事は main() に並び替え後の値を返していたわけでは無いので、
そこがイマイチのような気がしました。
そのため上図にあるように return nums として、
最終的には main() に値を返すようにしました。
def quick_sort(left,right,nums):
Cptr = (left+right)//2
Rptr = right
Lptr = left
while Lptr <= Rptr:
while nums[Lptr] < nums[Cptr]:Lptr += 1
while nums[Cptr] < nums[Rptr]:Rptr -= 1
if Lptr <= Rptr:
nums[Lptr],nums[Rptr] = nums[Rptr],nums[Lptr]
Lptr += 1
Rptr -= 1
if left < Rptr:
quick_sort(left,Rptr,nums)
if Lptr < right:
quick_sort(Lptr,right,nums)
return nums
if __name__ == "__main__":
nums = [1,8,7,4,5,2,6,3,9]
print(quick_sort(0,len(nums)-1,nums))
[1, 2, 3, 4, 5, 6, 7, 8, 9]